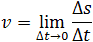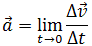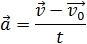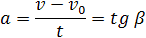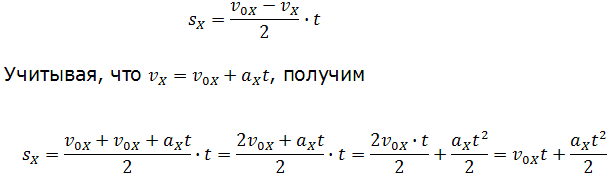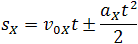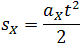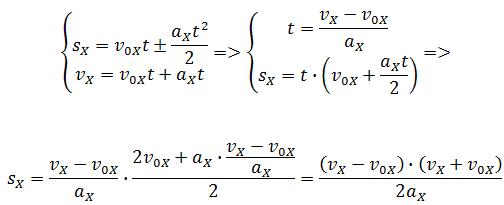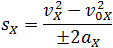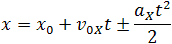Кинематические уравнения равнопеременного движения.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
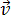
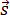
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
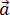
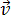
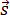
Учитывая, что 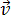
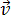
Отсюда формула скорости равнопеременного движения в любой момент времени:
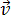
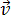
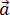
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
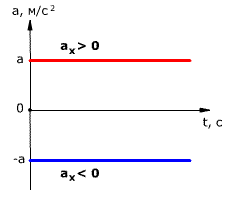
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
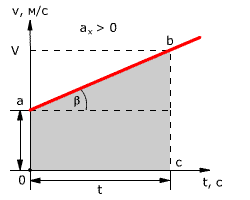
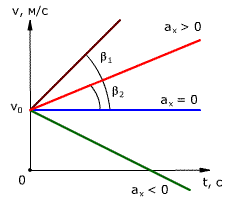
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
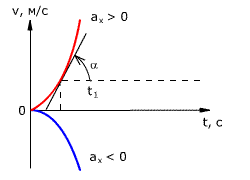
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратовпоможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, тоуравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
| | | следующая лекция ==> |
| | | Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. |
Дата добавления: 2016-01-29 ; просмотров: 7491 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнения равнопеременного движения
ФИЗИЧЕСКИЕ ОСНОВЫ
МЕХАНИКИ
Учебное пособие для студентов
института путей сообщения
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. Учебное пособие по физике для студентов института путей сообщения.
Учебное пособие представляет собой курс лекций по физике. Пособие написано в соответствии с программой для инженерно-технических специальностей высших учебных заведений. Однако, в отличие от Общего курса физики в данном учебном пособии дополнительно рассмотрены вопросы применения физических законов к процессам на железнодорожном транспорте. Таких как создание силы тяги локомотива, динамики поезда, динамики вагона, собственных и вынужденных колебаний вагона, колебаний тягового двигателя на рессорах подвески и т.д.
В конце каждой главы приведены контрольные задачи. Все формулы и решения задач приведены в Международной системе единиц СИ.
Авторы: А. В. Шушарин, ст. преподаватель кафедры ЕНД,
М.А. Круглова, доцент кафедры ЕНД.
Рецензенты: А.Е. Гришкевич, профессор кафедры
Общей и теоретической физики ЮУрГУ,
канд. физ.мат. наук;
В. Л. Федяев, доцент, зам. директора ЧИПС,
Печатается по решению научно-методического Совета
Челябинского института путей сообщения
Филиал Уральского государственного университета путей сообщения
Челябинский институт путей сообщения, 2010.
«Физика – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи, и законы её движения» (БСЭ).
Материя – это та реальность, из которой создан окружающий мир, которую можно обнаружить посредством ощущений. Материя существует в двух видах: как вещество и как силовые поля. Всякое изменение материи является движением. Простейшая форма движения материи – механическое движение – это процесс изменения взаимного расположения тел или их частей в пространстве с течением времени. Раздел физики, занимающийся изучением закономерностей механического движения, называется механикой.
Развитие механики, как науки, было вызвано потребностями техники и строительства. Древнейшие постройки Египта свидетельствуют о знании закона равновесия тел. Началом следует считать III в. до н.э., когда древнегреческий ученый Архимед сформулировал закон рычага и законы равновесия плавающих тел. Развитие механики было продолжено в 16 – 17 веках трудами Коперника, Кеплера, Гюйгенса, и особенно Галилея, впервые применившего экспериментальный метод исследования. Окончательно основные законы классической механики были экспериментально установлены и сформулированы И. Ньютоном в его многотомном труде «Математические начала натуральной философии» (1687 г.). В этом сочинении был воплощен идеал научной теории – отыскание количественных закономерностей в явлениях природы. Дальнейшее развитие механики шло по созданию аналитических методов решения задач, по созданию новых направлений механики. Развитие не прекращается и в наше время. В 20 веке были созданы новые области механики: релятивистская механика и квантовая механика, со своими законами и методами решения задач (рис.1).
В классической механике изучаются законы движения макроскопических тел со скоростью меньше скорости света (V 8 м/с) и на расстоянии до 10 22 м (но может быть и далее). Макроскопические тела это обычные тела, содержащие громадное количество молекул.
Закономерности механического движения микрообъектов (атомы, элементарные частицы) изучает квантовая механика.Критерием применения законов микромира является универсальная константа – постоянная Планка ћ =1,054·10 -34 Дж∙с. Если момент импульса частицы сопоставим с постоянной Планка, mVr ≈ ħ, то проявляются волновые свойства частиц, исчезает понятие траектории. Неизвестны законы движения на расстоянии менее, чем 10 -20 м. Может, здесь уже следует учитывать дискретность пространства и времени?
Закономерности 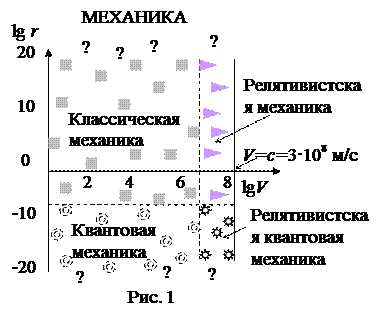
Квантовая механика и релятивистская механика являются более общими научными теориями, чем классическая механика. Они установили границы применения классической механики. Законы квантовой и релятивистской механики переходят в законы классической механики в предельном случае движения тел большой массы в большой области пространства с малыми скоростями. Но классическая механика не утратила своего значения с созданием более общих теорий, поскольку поправки новых теорий в задачах техники ничтожно малы.
Классическая механика подразделяется на три части. Кинематика (от греческого слова kinema – движение) – раздел механики, в котором изучаются законы движения тел без учета их массы и действующих на них сил. Динамика (от греческого dynamis – сила) изучает движения тел в связи с теми причинами, которые обусловливают это движение. Статика (от греческого statike – равновесие) изучает условия равновесия тел.
Механическое движение тел происходит в пространстве и времени. Эти понятия прочно связаны с нашим житейским опытом и кажутся нам очевидными и незыблемыми. Со времен Ньютона в классической механике постулируется, что пространство и время имеют абсолютный характер, т.е. существуют независимо друг от друга, от находящихся в них объектов и протекающих процессов. Но в ходе развития физики и философии эти понятия претерпели существенные изменения. В релятивистской механике пространство и время связаны между собой.
Пространство в классической механике однородно, изотропно и эвклидово (его геометрия описывается геометрией Эвклида). Однородность пространства означает, что любая его точка равноправна. То есть начало отсчета координатной системы можно перенести в любую точку пространства; этот перенос никак не влияет на процессы, происходящие с телом. Изотропность пространства означает равноправие всех направлений, то есть, если все оси системы координат повернуть, то это не изменит протекающие процессы. Время в классической механике – абсолютная реальность, не зависящая от тел, оно однородно и во всей Вселенной течет равномерно и одинаково. Однородность времени означает равноправность всех его моментов, т.е. время протекает непрерывно и одинаково от прошедшего к будущему, и любой из его моментов может быть выбран за начало отсчета любого процесса при одинаковых условиях.
Физика является фундаментальной наукой. Она является базой всех технических дисциплин, её законы используются в самых разных разделах науки и техники. Знание физики повышает кругозор образованного человека, он более критично относится к сверхновым теориям, к ложным наукам. Для специалиста путей сообщения особенно важна механика, так как движение транспортных средств на Земле вполне подчиняется законам классической механики. Прочное знание механики повышает компетентность специалиста при решении технических проблем.
Системы единиц измерения физических величин
Измерить какую-либо физическую величину — это значит сравнить ее с другой однородной физической величиной, принятой за единицу измерения. Единицы измерения сводятся в систему, охватывающую единицы всех физических величин и позволяющую оперировать с ними. Для построения системы произвольно выбирают единицы для нескольких не зависящих друг от друга величин. Эти величины называются основными. Остальные величины и их единицы выводятся из законов, связывающих их с основными единицами. Они называются производными.
Т.к. выбор основных единиц произволен, то может быть построен целый ряд систем единиц: СГС, СГСЭ, МКС, МКГСС и др. Во всем мире и в нашей стране (болеет 80 лет) в качестве предпочтительной принята Международная система единицСИ – единая система для всех разделов физики. В этой системе основными единицами измерения являются:
длины L – 1 метр (м), равный 1.650.763,73 длин волн излучения оранжевого цвета изотопа криптона 86 в вакууме;
массы m – 1 килограмм (кг), равный массе международного прототипа килограмма;
времени t – 1 секунда (с), равная 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133;
температуры T – 1 кельвин (К), равный 1/273,15 термодинамической температуры затвердевания дистиллированной воды при давлении 101 325 Па;
количества вещества v – 1 моль, содержащий столько атомов, сколько содержится в 0,012 кг нуклида углерода С12;
силы тока J – 1 ампер (А), который, проходя по двум параллельным | прямым проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенных на расстоянии 1 м в вакууме, вызывает силу 2∙10 -7 Н на каждый метр длины;
силы света I – 1 канделла (Кд), равная силе света в заданном на правлении источника, испускающего монохроматическое излучение частотой 540 · 10 12 Гц, энергетическая сила света которого в этом направлении составляет 1/ 683 Вт/ср.
Дополнительные единицы: рад (радиан) – единица плоского угла, ср (стерадиан) – единица телесного угла.
1. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Основные понятия кинематики
Существует два основных вида движения тел: поступательное и вращательное. При поступательном движении любая прямая, связанная с телом, остается параллельной самой себе, поэтому изучение движения тела сводится к изучению движения любой точки тела. Тело можно принять за материальную точку, масса которой равна массе тела. Материальной точкой называется макроскопическое тело, размеры и форму которого можно не учитывать в данной задаче. Например, движение поезда между станциями можно рассматривать как движение материальной точки.

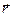


где 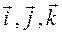

Если из этих уравнений исключить время t , мы получим уравнение траектории – линии, вдоль которой двигалось тело. Траектория – понятие относительное, форма траектория зависит от выбора системы отсчета. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Для рельсового транспорта траектория определяется расположением рельсов.
Параметрами поступательного движения материальной точки по траектории являются вектор перемещения и путь. Перемещение – это вектор, соединяющий начальную и конечную точки траектории (рис.1.1). Путь – это длина траектории или расстояние, проходимое телом от начала до конца движения. На рис 1.1 это длина пунктирной линии. Путь – величина скалярная и положительная. По величине путь и перемещение равны при прямолинейном движении в одном направлении или на бесконечно малом участке траектории.
Скорость
Быстрота изменения вектора перемещения во времени характеризуется скоростью. Мгновенная скорость 
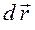

То есть скорость равна первой производной от вектора перемещения по времени. Вектор мгновенной скорости, как и вектор перемещения 
Продифференцировав по времени уравнение (1.1) получим уравнение для вектора скорости через проекции на оси координат
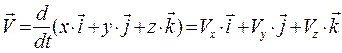
где 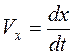
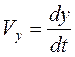

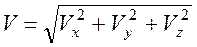
При бесконечно малом перемещении длина пути dS приближается к величине элементарного перемещения 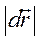
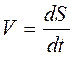
Неравномерное движение тела с переменной по величине скоростью характеризуют средней скоростью

По определению средняя скорость неравномерного движения равна отношению всего пути ко всему времени движения.
Ускорение
При движении тела скорость может быть не постоянна. Быстрота изменения скорости характеризуется ускорением. Ускорение,по определению, равно отношению бесконечно малого изменения вектора скорости 

То есть ускорение – это вектор, равный первой производной от вектора скорости по времени. Через проекции вектора ускорения на декартовы оси координат 


Кроме этого, принято представлять полное ускорение как векторную сумму составляющих ускорения на касательное и нормальное направление к траектории 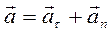
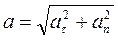
Представим вектор скорости, который направлен по касательной, как произведения модуля скорости на единичный вектор касательной 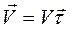
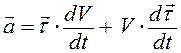
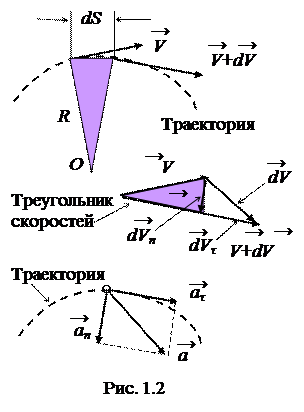
Первый член формулы характеризует изменение скорости по величине и определяет касательное ускорение 
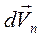
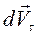

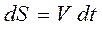
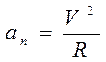
Уравнения равнопеременного движения
Движение точки называется равнопеременным, если вектор ускорения постоянен.
Так как, исходя из определения ускорения, элементарное приращение скорости равно 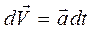
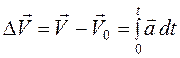
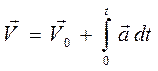
Элементарное изменение радиус-вектора точки, по определению скорости, равно 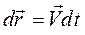
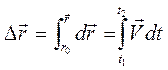
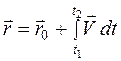
Применим эти уравнения для вывода скорости и радиус-вектора точки при равнопеременном движении. Равнопеременное движение – это движение с постоянным по величине и по направлению ускорением. Например, полет тела в поле тяжести Земли с ускорением свободного падения g = 9,81 м/с 2 .
Получим уравнение для скорости. Для этого проинтегрируем уравнение (1.9) при постоянном векторе ускорения, 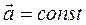
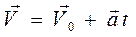
Подставив формулу скорости (1.11) под знак интеграла для вектора перемещения, получим основное кинематическое уравнение равнопеременного движения
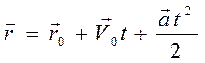
При решении конкретных задач векторные уравнения (1.11) и (1.12) проецируют на выбранные оси координат и получают систему уже алгебраических уравнений для решения задачи.
Теоретическая механика:
Кинематика точки
Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
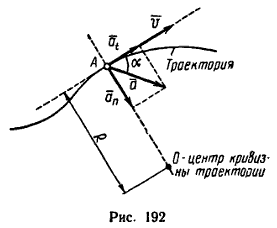
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f»(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at 2 + an 2 ).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
§ 27. Равномерное прямолинейное движение точки
Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .
Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.
В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.
§ 28. Равномерное криволинейное движение точки
Если at = 0 и an ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v 2 /R,
где R – радиус кривизны траектории.
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v 2 /r = const.
При равномерном движении числовое значение скорости определяется из формулы
v = (s — s0)/t или v = s/t.
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.
§ 29. Равнопеременное движение точки
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным .
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным .
При |at|>0 движение точки называется равноускоренным , а при |at| равнозамедленным .
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att 2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4) s = s0 + (v 2 — v0 2 ) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att 2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v 2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .
§ 30. Неравномерное движение точки по любой траектории
§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);
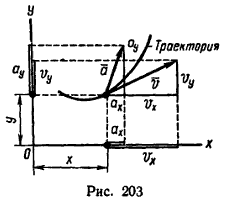
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме .
Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;
б) числовое значение скорости точки находится из формулы
v = sqrt(vx 2 + vy 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;
в) числовое значение ускорения находится из формулы
a = sqrt(ax 2 + ay 2 )
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
§ 32. Кинематический способ определения радиуса кривизны траектории
При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v 2 /R,
выражающую числовое значение нормального ускорения.
Скорость v точки определяется по формуле
(б) v = sqrt(vx 2 + vy 2 ).
Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an 2 + at 2 ),
откуда
(в) an = sqrt(a 2 — at 2 ),
где квадрат полного ускорения
(г) a 2 = ax 2 + ay 2
и касательное ускорение
(д) at = dv/dt.
Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1‘(t);
vy = f2‘(t).
2. Подставив в (б’) выражения vx и vy, найти v 2 .
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение at, а затем at 2 .
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1»(t) = vx‘;
ay = f2»(t) = vy‘.
5. Подставив в (г) выражения ax и ay, найти a 2 .
6. Подставить в (в) значения a 2 и at 2 и найти an.
7. Подставив в (а) найденные значения v 2 и an, получить радиус кривизны R.
http://lektsii.org/6-70014.html
http://exir.ru/termeh/kinematika_tochki.htm