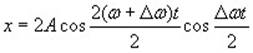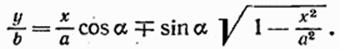Вывод уравнения биения и его анализ

Вывод уравнения биения и его анализ

Название работы: Сложение гармонических колебаний

Предметная область: Физика

Описание: Тема: Сложение гармонических колебаний Сложение гармонических колебаний одного направления и одинаковой частоты, условия усиления и ослабления. Биения. Уравнение биений и его анализ. Сложение взаимно перпендикулярных колеба.

Дата добавления: 2013-02-24

Размер файла: 170.5 KB

Работу скачали: 93 чел.

Тема: Сложение гармонических колебаний

1. Сложение гармонических колебаний одного направления и одинаковой частоты,

1. Биения. Уравнение биений и его анализ.

1. Сложение взаимно перпендикуляр-ных колебаний.

1. Сложение гармонических колебаний одного направления и одинаковой частоты, условия усиления и ослабления.

Под сложением колебаний понимают нахождение уравнения результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Пример таких колебаний приведен на рисунке. В этом случае грузик 2 одновременно колеблется относительно грузика 1 на пружине b и вместе с ним на пружине a .

Для получения уравнения результирующих колебаний используем метод вращающегося вектора амплитуды. На рисунке показаны векторы А 1 и А 2 , положения которых заданы фазами Ф 1 и Ф 2 в некоторый момент времени. Проекции этих векторов на выбранную ось определяют смещения S 1 ( t ) и S 2 ( t ), которые изменяются по гармоническому закону

Амплитуда А р результирующих колебаний равна векторной сумме амплитуд А 1 и А 2 . Для определения амплитуды А р результирующих колебаний запишем теорему косинусов для треугольника ОАА 1

Учитывая то, что , получим формулу для амплитуды А р результирующих колебаний

где Δ Ф – разность фаз складываемых колебаний.

Фаза Ф р результирующих колебаний определяется следующей формулой

Уравнение результирующих колебаний записывается в следующем виде

где А р и Ф р определяются формулами (3) и (4).

Таким образом, амплитуда А р результирующих колебаний (и результирующее смещение) определяется разностью фаз складываемых колебаний

Из формулы (6) видно, что если частоты складываемых колебаний равны ( ω 1 = ω 2 ), то разность их фаз не зависит от времени и определяется разностью начальных фаз

Тогда и амплитуда результирующих колебаний не будет зависеть от времени, т.е. будет постоянной. В этом случае два колебания совершаются согласованно во времени и их называют когерентными .

Когерентными называются колебания, для которых разность фаз постоянна.

Гармонические колебания с одинаковыми частотами являются когерентными.

При сложении гармонических колебаний одного направления и одинаковой частоты результирующее колебание также является гармоническим.

Различают два случая.

1. Разность фаз складываемых колебаний равна нулю или четному числу π

, где n = 0, 1, 2, 3… (7)

В этом случае при любом целочисленном значении n и по формуле (3) получим для результирующей амплитуды

Таким образом, при выполнении условия (7) колебания совершаются в одинаковой фазе и усиливают друг друга . Поэтому условие (7) называют условием усиления колебаний одного направления при их сложении.

1. Разность фаз складываемых колебаний равна не четному числу π

, где n = 0, 1, 2, 3… (8)

В этом случае при любом целочисленном значении n и по формуле (3) получим для результирующей амплитуды

Таким образом, при выполнении условия (8) колебания совершаются в противофазе и ослабляют друг друга. Поэтому условие (8) называют условием ослабления колебаний одного направления при их сложении.

Читателю предлагается самому посмотреть как влияют амплитуды А 1 и А 2 и начальные фазы φ 01 и φ 02 гармонических колебаний на результат сложения гармонических колебаний одного направления и одинаковой частоты.

Для этого необходимо навести курсор на диаграмму и двойным «клик» активизировать ее. Затем в открывшемся окне изменять значения указанных величин, приведенных в цветных ячейках. По окончанию работы с графиком таблицу EXEL закрыть с сохранением или без сохранения данных.

1. Биения. Уравнение биений и его анализ.

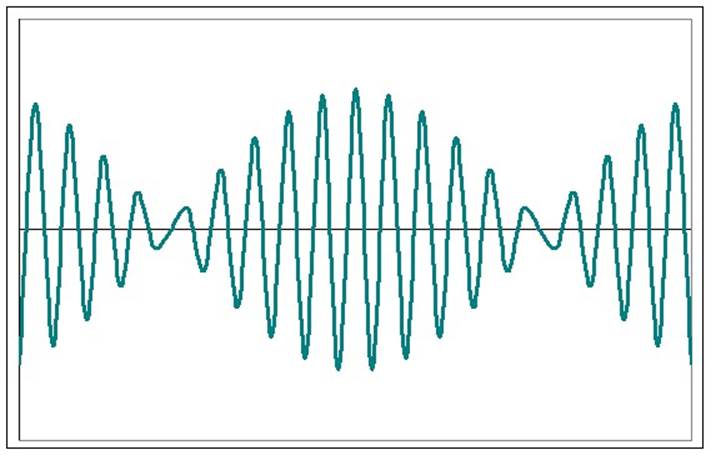
При сложении колебаний одного направления, но с неодинаковыми частотами разность фаз Δ Ф (формула 6) будет изменяться с течением времени. Каждый из векторов А 1 и А 2 будет вращаться с разной скоростью и амплитуда результирующих колебаний будет изменяться с течением времени. В этом случае колебания не будут когерентными , и результирующее колебание не будет гармоническим. При большом отличии значений частот ω 1 и ω 2 получается довольно сложное результирующее колебание. Например, при ω 1 = 9 ω 2 график результирующего колебания имеет вид, показанный на рисунке.

Большой практический интерес представляет собой сложение гармонических колебаний одного направления с близкими частотами . Для простоты рассмотрим колебания с одинаковыми амплитудами А 1 = А 2 = А и начальными фазами, равными нулю . В этом случае уравнение результирующих колебаний будет иметь следующий вид ( уравнение биений )

При близких значениях частот ω 1 и ω 2 первый сомножитель

будет медленно и периодически изменяться с течением времени, и график результирующих колебаний будет иметь следующий вид (для одного периода биений).

В данном случае модуль величины, определяемой формулой (10) условно рассматривают как амплитуду А ( t ) результирующего колебания

Уравнение результирующих колебаний записывается в следующем виде

Рассмотренные колебания называются биением, а (12) называется уравнением биений .

Биением называется явление периодического изменения амплитуды результирующих колебаний, возникающее при сложении двух гармонических колебаний одного направления с близкими частотами.

Значение частоты Ω б , равное разности частот ω 1 и ω 2 складываемых колебаний называется частотой биений

Учитывая связь между циклической частотой и периодом можно получить следующую формулу для периода биений

Из формулы (13) видно, что по мере сближения частот ω 1 и ω 2 частота биений уменьшается, обращаясь в ноль при ω 1 = ω 2 . На этом основан один из точных методов определения частоты неизвестных колебаний. В этом методе неизвестные колебания складываются с колебаниями регулируемой частоты, и измеряется частота биений. Неизвестную частоту определяют по исчезновению биений.

Читателю предлагается самому посмотреть как влияют периоды Т 1 и Т 2 и начальные фазы φ 01 и φ 02 гармонических колебаний на результат сложения гармонических колебаний одного направления с близкими частотами.

Для этого необходимо навести курсор на диаграмму и двойным «клик» активизировать ее. Затем в открывшемся окне изменять значения величин, приведенных в цветных ячейках. По окончанию работы с графиком таблицу EXEL закрыть с сохранением или без сохранения данных.

1. Сложение взаимно перпендикулярных колебаний.

Пусть точка одновременно участвует в гармонических колебаниях вдоль двух взаимно перпендикулярных направлений. Например, такое движение будет совершать «изображение» электронного луча на экране осциллографа, если на горизонтальные и вертикальные отклоняющие пластины подать гармонически изменяющиеся напряжения.

Свяжем направления колебаний точки (светового пятна) с прямоугольной системой координат, начало которой совпадает с положением равновесия. Смещения точки вдоль осей ОХ и О Y обозначим буквами x и y соответственно. Тогда уравнения рассматриваемых колебаний можно записать в следующем виде

Уравнение результирующего движения получают исключением времени t из уравнений (15). В случае, когда значения частот складываемых колебаний не одинаковые, уравнение результирующего движения имеет довольно сложный вид. Это уравнение упрощается при равенстве значений частот ( ω 1 = ω 2 = ω ). В этом случае уравнение результирующего движения (уравнение траектории) принимает следующий вид

Вывод уравнения (16) можно найти в книгах (А.А. Детлаф, Б.М. Яворский. Курс физики, или Т.И. Трофимова. Курс физики). Только нужно учесть, что в книге Т.И. Трофимовой в формуле (145.2) под величиной φ следует понимать разность начальных фаз складываемых колебаний.

Уравнение (16) показывает, что в общем случае, в результате сложения взаимно перпендикулярных гармонических колебаний одинаковой частоты точка будет описывать эллипс с произвольной ориентацией осей. Ориентация осей эллипса, а также его размеры определяются значениями амплитуд А 1 , А 2 и разности начальных фаз ( φ 02 – φ 01 ) складываемых колебаний.

Рассмотрим некоторые частные случаи:

В этом случае третье слагаемое уравнения (16) обращается в ноль, правая часть равняется единице и получается уравнение эллипса, оси которого совпадают с осями координат ОХ и О Y , а размеры полуосей равны амплитудам А 1 и А 2

При этом, если А 1 = А 2 , то уравнение (18) переходит в уравнение окружности. Т.е. точка будет описывать окружность

В данном случае правая часть уравнения (16) обращается в ноль, и уравнение (16) переходит в уравнение прямой

Т.е. точка будет гармонически колебаться с частотой ω и амплитудой вдоль прямой, составляющей с осью ОХ угол α , равный .

Таким образом, в зависимости от значений амплитуд и разности фаз складываемых взаимно перпендикулярных колебаний результирующее колебание будет происходить по эллипсу, по окружности или вдоль прямой линии. Такие колебания называются эллиптически поляризованными, циркулярно поляризованными или линейно поляризованными соответственно.

Если частоты складываемых взаимно перпендикулярных колебаний не равны, то получаются замкнутые траектории сложной формы, которые называются фигурами Лиссажу (по фамилии французского физика Ж. Лиссажу (1822-1880)). Форма фигур Лиссажу определяется соотношением значений амплитуд, частот и начальных фаз складываемых колебаний. По форме фигуры Лиссажу можно определить значение частоты одного из колебаний, если известно значение частоты другого колебания.

Читателю предлагается самому посмотреть как влияют амплитуды А 1 и А 2 , периоды Т 1 и Т 2 и начальные фазы φ 01 и φ 02 гармонических колебаний на результат сложения взаимно перпендикулярных колебаний.

Для этого необходимо навести курсор на диаграмму и двойным «клик» активизировать ее. Затем в открывшемся окне изменять значения величин, приведенных в цветных ячейках.

Сначала предлагается при равенстве периодов Т 1 и Т 2 изменять амплитуды и начальные фазы и проверить справедливость формул (17-21). После чего последовательно изменяя значения всех параметров наблюдать фигуры Лиссажу.

По окончанию работы с графиком таблицу EXEL закрыть с сохранением или без сохранения данных.

Вопросы для самопроверки:

1. Какие колебания называются когерентными?
2. При каких условиях сонаправленные колебания будут усиливать либо ослаблять друг друга?
3. Что называется биением? Какой формулой определяется частота биений?
4. При каких условиях получаются эллиптически, циркулярно или линейно поляризованные колебания

Амплитуда биения. Сложение взаимно перпендикулярных колебаний

Векторная диаграмма.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой [1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.

Сложение нескольких гармонических колебаний одного направления.

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

(4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

(4.2)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω

Биения, Период биения.

Бие́ния — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала.Частота изменения амплитуды суммарного сигнала равна разности частот исходных сигналов.

Период биений Т_б — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.

Амплитуда биения. Сложение взаимно перпендикулярных колебаний.

Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где — разность фаз обоих колебаний.

Выражения (57.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (57.1) параметр t. Из первого уравнения следует, что

Теперь развернем косинус во втором из уравнений (57.1) по формуле для косинуса суммы, подставляя при этом вместо их значения (57.2) и (57.3). В результате получим

Последнее уравнение после несложных преобразований можно привести к виду

Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а и b и разности фаз

Определим форму траектории для некоторых частных случаев.

1. Разность фаз а равна нулю. В этом случае уравнение (57.4) принимает вид

откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой и амплитудой, равной (рис. 57.1).

2. Разность фаз а равна Уравнение (57.4) имеет вид

откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 57.2)

3. При уравнение (57.4) переходит в

т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний.

При равенстве амплитуд а и эллипс вырождается в окружность.

Случаи отличаются направлением движения по эллипсу или по окружности. Если уравнения (57.1) можно записать следующим образом:

В момент тело находится в точке (рис. 57.3). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке.

При уравнения колебаний имеют вид

Отсюда можно заключить, что движение происходит против часовой стрелки.

Из сказанного следует, что равномерное движение по окружности радиуса R с угловой скоростью со может быть представлено как сумма двух взаимно перпендикулярных колебаний:

(57.10)

(знак «+» в выражении для у соответствует движению против часовой стрелки, знак «—» — движению по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:

и выражение рассматривать как разность фаз, медленно изменяющуюся со временем по линейному закону.

Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от до

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 57.4 показана одна из простейших траекторий, получающаяся при отношении частот 1 : 2 и разности фаз Уравнения колебаний имеют вид

За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение.

При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 57.5), по которой точка движется туда и обратно.

Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 57.6 для примера показана кривая для отношения частот 3 : 4 и разности фаз .

Биения. Уравнение биений

Биения. Уравнение биений — раздел Механика, Механические колебания Для Практики Особый Интерес Представляет Случай, Когда Два Складываемых Гармо.

Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте w₁ ≈ w₂. Получим уравнение результирующего колебания для этого случая.

Примем, что амплитуды складываемых колебаний равны А, а частоты: w₁ = w, w₂ = w + Δw, причём Δw « w. Начало отсчёта выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

(30)

Складываем эти выражения, применяя формулу суммы косинусов.

Учитывая, что Δw « w и, пренебрегая Δw в сравнении с w, получаем:

.

Из анализа полученного выражения видно, что сомножитель, стоящий в скобках, меняется гораздо медленнее, чем второй сомножитель. И пока сомножитель в скобках совершит один полный цикл своих изменений, второй сомножитель сделает несколько колебаний.

Это даёт основание рассматривать результирующее колебание х как гармоническое с частотой w и амплитудой А_б, которая изменяется по периодическому закону:

_.

Такие изменения амплитуды называются биениями.

Эта тема принадлежит разделу:

Механические колебания

Механические колебания.. основные определения и.. вынужденные колебания..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Биения. Уравнение биений

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Основные определения и понятия
Колебаниями называется вид движения физических тел или такие процессы, для которых характерна та или иная степень повторяемости во времени. Например, принципом

Гармонические колебания
Получим закон гармонических колебаний на примере механического движения механических колебаний. Это вид колебаний, при котором тело поочерёдно и многократно совершает отклонения от своего положения

Затухающие гармонические колебания
В реальных условиях, кроме возвращающей силы в колебательной системе обязательно будет действовать и сила сопротивления. Будем считать, что скорости движения при колебаниях будут не

Колебания, которые совершаются под воздействием переменной силы, называются вынужденными
Рассмотрим колебания под воздействием вынуждающей силы, изменяющейся по гармоническому закону: F = F○соsωвt. (22)

Сложение взаимноперпендикулярных колебаний
Рассмотрим случай сложения двух гармонических взаимно-перпендикулярных колебаний одинаковой частоты w, совершающихся вдоль координатных осей х и у. Для простоты, начал

Сложное колебание и его гармонический спектр
Если частоты складываемых колебаний не равны друг другу ω1 ≠ ω2 , то результирующее колебание не будет гармоническим, а его амплитуда будет не постоянна. Такое