Вывод уравнения динамики вращательного движения материальной точки

Вывод уравнения динамики вращательного движения материальной точки

Название работы: Вывод основного закона динамики вращательного движения

Предметная область: Физика

Описание: Вывод основного закона динамики вращательного движения. К выводу основного уравнения динамики вращательного движения. Динамика вращательного движения материальной точки. В проекции на тангенциальное направление уравнение движения примет вид: Ft = mt.

Дата добавления: 2013-09-05

Размер файла: 29 KB

Работу скачали: 198 чел.

15.Вывод основного закона динамики вращательного движения.

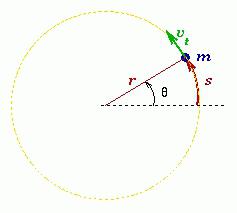
Рис. 8.5. К выводу основного уравнения динамики вращательного движения.

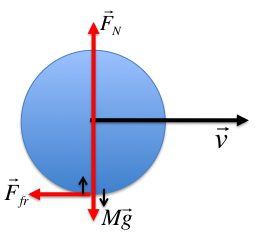
Динамика вращательного движения материальной точки. Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R , под действием результирующей силы F (см. рис. 8.5). В инерциальной системе отсчета справедлив 2 ой закон Ньютона. Запишем его применительно к произвольному моменту времени:

Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид:

Поскольку a t = e·R, то

Умножив левую и правую части уравнения скалярно на R, получим:

F t ·R= m·e·R 2 (8.7)
M = I·e. (8.8)

Уравнение (8.8) представляет собой 2 ой закон Ньютона (уравнение динамики) для вращательного движения материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора углового ускорения, направленного вдоль оси вращения (см. рис. 8.5):

Основной закон динамики материальной точки при вращательном движении можно сформулировать следующим образом:

произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.

Динамика вращательного движения материальной точки

Лк-3.

Сила тяжести – частный вид гравитационной силы. Величина гравитационной силы притяжения двух точечных масс m₁ и m₂ определена Ньютоном и известна как закон всемирного тяготения:

, (3.1)

где r — расстояние между массами, а G = 6,67 10 -11 Нм 2 /кг 2 — гравитационная постоянная. В частности, для силы тяжести на поверхности земли:

( 3.2 )

Откуда определится формула для ускорения свободного падения:

Радиус земли известен R_земл=6380 км. Данная формула позволяет вычислить массу земли.

Динамика вращательного движения материальной точки

Рассмотрим ситуацию вращательного движения материальной точки с массой m вокруг оси, которую для определенности направим вертикально, как показано на рис. 2.5. Линейная скорость движения точки по окружности — v связана с угловой скоростью — ω формулой (2…)

Импульс точки . Назовем моментом импульса величину

(3.3)

Подставим в (2.14) вместо р его выражение через линейную скорость:

(3.4)

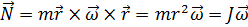
Величина 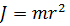называется моментом инерции материальной точки, а формула (3.4) по форме аналогична формуле импульса, в которую вместо массы точки подставлен ее момент инерции, а вместо скорости — угловая скорость. Продифференцируем по времени (3.4)

Первое слагаемое в правой части равно нулю, так как векторы импульса — р и скорости dr/dt параллельны. Во втором слагаемом производная от импульса, согласно второму закону Ньютона, представляет силу, действующую на точку. Следовательно

(3.5)

(3.6)

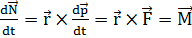
называется моментом силы F относительно оси вращения. Таким образом, производная по времени от момента импульса равна моменту силы. Вновь получаем аналогию с поступательным движением, при котором производная по времени от импульса равна силе.

С другой стороны, взяв производную по времени от (3.4), получим

, где ε — угловое ускорение. Заменив dN/dt моментом силы, получим аналог второго закона Ньютона для вращательного движения:

(3.7)

Все формулы для вращательного движения материальной точки легко запомнить, поскольку по форме они аналогичны формулам поступательного движения. Необходимо только заменить массу на момент инерции, силу — на момент силы, скорость — на угловую скорость, импульс — на момент импульса.

Поступательное движение	Вращательное движение
Масса m	Момент инерции j=mr 2
Линейная скорость	Угловая скорость
Линейное ускорение	Угловое ускорение
Сила	Момент силы
Импульс	Момент импульса
Основное уравнение динамики	Основное уравнение динамики

Пример: Качание тела, подвешенного на нити длиной l, является движением по окружности с центром в точке подвеса. Составить уравнение движения тела, используя в качестве координаты угол отклонения нити от вертикали. Поместим начало координат в точку подвеса — О. Координатой материальной точки будет угол α между нитью подвеса и вертикалью. Этот угол мы считаем векторной величиной, причем направлен этот вектор перпендикулярно плоскости рисунка от нас. В ту же сторону направим ось Z. Очевидно, что точка будет совершать колебательное движение по окружности с радиусом |r|. Составим уравнение движения. Само уравнение движения очень простое, его можно записать в форме (3.7). Однако, для этого необходимо выразить векторы момента силы и углового ускорения через данные задачи. Мы считаем данными длину нити подвеса |r|=l. Обозначим через m массу мат. точки.

Момент силы тяжести:

Момент инерции J=m|r| 2 =ml 2

Уравнение движения:

Подставим это в уравнение движения

После сокращения на m приходим к выводу о том, что масса точки не влияет на характер движения.

При работе с векторами на какой-то стадии требуется переход к скалярным величинам. Этот переход осуществляется путем проецирования векторов на произвольно выбранную ось. Умножим левую и правую части векторного уравнения на единичный вектор оси, перпендикулярной плоскости рисунка.

Векторное произведение направлено против оси Z, поэтому . Вектор углового ускорения со направлен с осью Z, поэтому . В результате получим скалярное уравнение

Это и есть искомое уравнение движения. Его нужно сократить на l и вместо углового ускорения — ε подставить вторую производную по времени от угла α:

Если решить это уравнение, то мы получим зависимость угла α от времени. Из вида уравнения следует, что единственным параметром этой зависимости является отношение g/l.

Работа и энергия. Элементарной работой dA силы F на перемещении dl называется их скалярное произведение ( см. рис):

(3.8)

В декартовой системе координат величину элементарной работы ( по правилам записи скалярного произведения ) можно записать в следующем виде:

где F_x , F_y , F_z — проекции силы на оси координат и dx, dy, dz — cоответствующие проекции перемещения. Для подсчета работы переменной силы на конечном перемещении необходимо просуммировать все элементарные работы

Когда суммируются бесконечно много бесконечно малых слагаемых типа , вместо значка Σ используется значок ∫, а вместо индекса суммирования –i указываются начальная и конечная точки пути, например a и b. В результате запись формулы для работы примет следующий вид:

Размерность работы [Н*м] называется Джоулем: 1Дж=1Н*1м.

Пятиминутка. Человек везет сани, как показано на рисунке. Пройденный путь – 1 км, модуль приложенной силы 10 Н, угол α=60 о . Вычислить совершенную работу.

Кинетическая энергия. Если на тело массы m действует некоторая сила F, сообщая ему ускорение — а, то эта сила совершает работу, которая связана с изменением скорости тела. Вычислим элементарную работы на участке траектории dl.

Поменяем местами множители в скалярном произведении:

Скалярное произведение v*dv представляет собой произведение модуля скорости — v на проекцию приращения скорости на направление вектора скорости. Эта проекция называется тангенциальным приращением скорости, которое равно увеличению ее модуля. Следовательно

Или так: . В данном случае v – это модуль скорости. Определим скалярную величину, производная от которой по модулю скорости равна mv, и назовоем ее кинетической энергией.

Эта величина называется кинетической энергией движущегося тела. Поскольку и , мы приходим к выводу о том, что dA=dW_к. Элементарная работа, совершенная силой, разгоняющей материальную точку, перешла в приращение кинетическую энергию этой точки. Этот же вывод справедлив и на конечном участке траектории: работа, совершенная разгоняющей силой равна приращению кинетической энергии тела.

Пятиминутка. Тело массой 1 кг брошено горизонтально с начальной скоростью 50 м/с. Вычислить работу силы тяжести и кинетическую энергию в конце 2 секунды движения.

Потенциальная энергия. Во многих случаях сила, действующая на тело, оказывается зависимой от его положения, от координат тела. И величину силы вдоль координатной оси можно вычислить путем дифференцирования некоторой величины по этой координате.

(3.12)

В этом случае сила называется потенциальной, а величина U – потенциальной энергией тела.

Элементарная работа потенциальной силы

Т.е. равна убыли потенциальной энергии тела.

В качестве примера рассмотрим вычисление работы центральной силы, т.е. силы, которая действует по прямой, соединяющей два взаимодействующих тела (материальные точки), и величина этой силы зависит только от расстояния между ними. 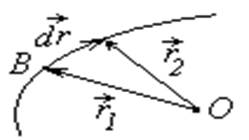Пусть материальная точка О действует на другую точку В центральной силой F. Точка В перемещается из положения 1 с радиусом-вектором r₁ в близкую точку 2 , радиус-вектор которой — r₂ ( см. рис.3.2 ). Перемещение точки В равно dr и формула для элементарной работы запишется в обычном виде:

Так как сила является центральной она направлена вдоль радиус-вектора, поэтому скалярные произведения и оказываются равными произведениям модулей силы и радиус-вектора. Тогда

(3.11)

где dr — приращение расстояния между взаимодействующими точками на малом участке траектории. Знак ± соответствует двум возможным знакам скалярного произведения Если вектор силы параллелен радиус-вектору , косинус угла между ними равен 1, ставится знак +. Это случай отталкивания между телами. Если же вектор анти параллелен радиус-вектору , угол между ними равен π, а косинус его равен -1. Этот случай соответствует притяжению между телами, ему соответствует знак -. Работа центральной силы на конечном участке траектории между точками 1-2 находится суммированием всех элементарных работ, с учетом того. что величина силы зависит от расстояния между телами, т.е.

(3.12)

где U( r ) — потенциал силы.

Из (3.12) видно, что работа центральной силы не зависит от формы траектории и определяется только расстояниями между взаимодействующими мат. Поскольку ребота потенциальных сил не зависит от формы траектории, а определяется только положением начальной и конечной точки, работа потенциальной на траектории, где начальная и конечная точки совпадают, равна нулю.

Для силы тяготения земли, которая является центральной силой, работа при увеличении расстояния от земной поверхности от r₁ до r₂ согласно выражению (3.12) равна:

В частности, если r₁=R₃ — радиусу земли, а r₂=∞, т.е. тело удаляется от земли в бесконечность, сила притяжения совершает работу

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

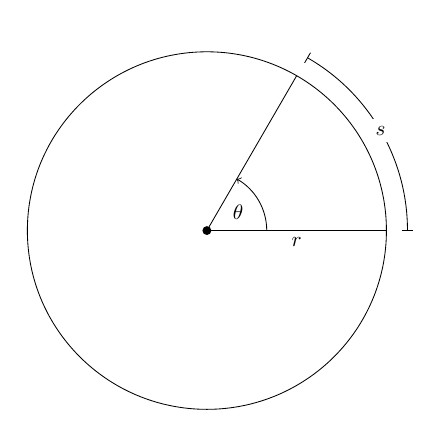
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

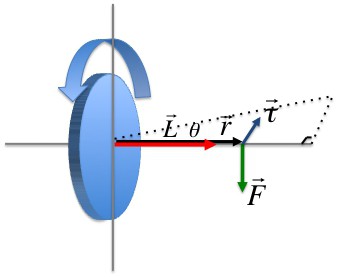
Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma 2 ,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).