Вывод уравнения фурье кирхгофа для теплопроводности

Теплоотдача (конвективный теплообмен)

4.2.1. Определение исходных понятий

Обмен внутренней энергией между поверхностью твердого тела и жидкостью посредством теплопередачи в теплотехнике называется теплоотдачей или конвективным теплообменом. Термин «конвективный теплообмен» подчеркивает, что процесс переноса тепла здесь осуществляется одновременно не только теплопроводностью, но и конвекцией. Теплопроводность обусловливается градиентом температуры между слоями жидкости. Конвективные потоки макроскопических элементов жидкости (газа) возникают вследствие различия в плотности вещества разных элементов, находящихся при разной локальной температуре. Конвекция, обусловленная разницей в плотности макроскопических элементов жидкости, называют естественной конвекцией. В жидкости можно реализовать также и вынужденную конвекцию с помощью внешних возбудителей, например, перемешиванием жидкости (газа).

Теплоотдача зависит и от характера движения жидкости – ламинарного (слоистого) или турбулентного (вихревого). Напомним, критерий перехода ламинарного течения в турбулентное оценивается безразмерным числом Рейнольдса Re = , где r — плотность жидкости, h — вязкость жидкости, v – средняя скорость потока жидкости, l – характерные размеры канала (например, диаметр трубы). При больших числах Рейнольдса наблюдается турбулентное течение. Экспериментально выявлено, что критическое значение числа Рейнольдса, когда в круглой трубе происходит переход от ламинарного течения в турбулентное, примерно2×10 3 . Характер течения жидкости (газа) в трубах разного сечения будет одинаков, если каждому сечению соответствует одно и то же значение числа Re.

При любом виде течения (турбулентном или ламинарном) скорость жидкости в тонком слое у стенки канала равна нулю. Этот слой обычно называют вязким подслоем. На рис. 4-6 приведен график изменения температуры в жидкости при турбулентном течении. Температура в основном изменяется по толщине вязкого слоя, а в турбулентном потоке изменение температуры незначительное.

Теплопередача в вязком подслое осуществляется теплопроводностью, термическое сопротивление которого представляет собой малую величину (см. формулу 7 * ). При ламинарном течении теплопередача в поперечном сечении канала трубы также осуществляется практически только за счет теплопроводности. При турбулентном течении вдали от стенки теплоотдача в объеме жидкости происходит в основном вследствие перемешивания элементов жидкости и температура в турбулентном слое по сечению трубы изменяется незначительно.

Явление теплоотдачи определяется тепловыми и гидродинамическими процессами. Эти процессы описываются соответствующими дифференциальными уравнениями: уравнением теплоотдачи, уравнением теплопроводности, уравнением динамики течения жидкости (газа), уравнением непрерывности. Рассмотрим эти уравнения.

4.2.2. Уравнение теплоотдачи

Интенсивность теплоотдачи (конвективного теплообмена) с поверхности стенки площадью dS за время t описывается эмпирической формулой Ньютона-Рихмана

где: T_ст , T_ж — температура стенки и жидкости соответственно; dS — элементарная площадка стенки; a — коэффициент теплоотдачи. Коэффициент теплоотдачи имеет смысл тепла, передаваемого в жидкость за единицу времени единицей поверхности при разности температур в один кельвин (один градус 0 С).

Теплопередача осуществляется через вязкий подслой толщиной l, для которой справедлив закон Фурье

dQ= — l t dS ,

где — градиент температуры в вязком подслое.

Сравнивая законы Ньютона-Рихмана и Фурье, получим:

a = — 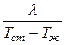. (23)

Уравнение (23) называется уравнение теплоотдачи. Уравнение теплоотдачи позволяет по известному температурному полю определить коэффициент теплоотдачи. Заметим, в технических расчетах процесса теплоотдачи именно коэффициент теплоотдачи и представляет наибольший интерес.

4.2.3. Уравнение теплопроводности Фурье-Кирхгофа

Выделим в потоке жидкости элементарный кубик с ребрами dx, dy, dz (рис. 4-7) и определим поток тепла через грани этого элементарного кубика.

Пренебрежем изменением давления p и будем считать, что параметры жидкости – коэффициент теплопроводности l, плотность r и удельная теплоемкость жидкости при постоянном давлении с_р – постоянные константы. Из первого начала термодинамики следует, что при p = const подведенная теплота равна приращению энтальпии в выделенный объем жидкости:

Здесь оператор d указывает, что теплота является одной из функций процесса переноса внутренней энергии (наряду с работой dA = pdV): элементарная порция подведенной теплоты dQ в общем случае не является полным дифференциалом. Однако так как энтальпия (H = U + pV) как функция состояния является полным дифференциалом, то припостоянном давлении подведенная элементарная порция тепла dQ формально становится полным дифференциалом, т.е. можно формально записать: dQ = dQ.

Поток тепла через грани кубика обусловлен градиентом температуры на противоположных гранях, находящихся в перпендикулярном направлении на расстоянии dx, dy и dz соответственно. Если в направлении x на левой грани (см. рис. 4-7) температура T, то на противоположной грани на расстоянии dx температура равна (T + dx), где – соответствующий градиент температуры. Аналогично по направлениям y и z.

За время dt в направлении оси x количество тепла, проходящее через левую грань, равно (закон Фурье)

Q_x1 = 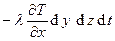, где dS = dx dy – площадь грани,

а через правую грань Q_x2 = .

Имеем: dQ_x = Q_x1 — Q_x2 = .

Аналогично по осям y и z:

dQ_y = , dQ_z = .

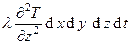
За счет подвода тепла наблюдаем приращение энтальпии жидкости за время dt определится уравнением

dQ = dH = dQ_x + dQ_y + dQ_z = . (24)

С другой стороны подведенную теплоту dQ (изменение энтальпии dH) можно представить также уравнением

dQ =c_pr dx dy dz, (25)

где dm = r dx dy dz – масса рассматриваемого элементарного объема, c_p – теплоемкость жидкости при постоянном давлении, – изменение температуры рассматриваемого объема за время dt вследствие притока тепла.

Здесь имеет смысл субстанциальной производной. Дело в том, что изменение температуры в текущей жидкости определяется двумя факторами: 1) изменением температуры во времени в рассматриваемом объеме жидкости; 2) изменением температуры вследствие перемещения этого объема от одной точки пространства к другой:

= + + + .

Здесь — локальное изменение температуры во времени (изменение температуры в данной точке пространства). Величина

+ + = + + ,

представляет собой конвективное изменение температуры, обусловленное перемещением элементов текущей жидкости (v_x, v_y, v_z – проекции скорости элементов жидкости). Таким образом, температурное поле в движущейся жидкости зависит и от распределения скоростей элементов жидкости.

Сравнивая (24) и (25) получим уравнение

c_pr dx dy dz = или

= . (26)

Уравнение (26) есть дифференциальное уравнение теплопроводности Фурье-Кирхгофа, где постоянная жидкости a = называется коэффициентом температуропроводности. Из уравнения Фурье-Кирхгофа следует, что коэффициент температуропроводности a характеризует скорость изменения температурного поля в среде. Уравнение (26) можно кратко записать посредством оператора Лапласа Ñ 2 = + + :

= . (26 * )

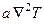
Запишем уравнение Фурье-Кирхгофа в развернутом виде

+ + + = . (26 ** )

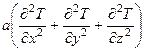
Для твердых тел уравнение Фурье-Кирхгофа пример вид

= ,

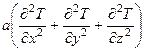
так как в твердых телах при наличии переноса тепла наблюдается только локальные изменения температуры, но перенос вещества отсутствует

4.2.4. Уравнение Навье-Стокса (дифференциальное уравнение

Движения жидкости)

Как было уже отмечено, из уравнения Фурье-Кирхгофа следует, что температурное поле зависит от распределения скоростей элементов жидкости (см., напр., уравнение 26 ** ). Динамика движения произвольного элемента жидкости массой dm описывается вторым законом Ньютона: dma = R, где R – результирующая сила, действующая на элемент.

Выделим в потоке жидкости элемент жидкости массой dm в форме кубика с ребрами dx, dy, dz (рис. 4-8). Жидкость течет по вертикали вниз. Ось 0x совпадает с левой стенкой. Скорость тонкого пристеночного слоя жидкост равна нулю. По мере удаления от стенки скорость v_x возрастает (на рисунке приведена эпюра скоростей жидкости).

На выделенный элемент жидкости действуют: 1) сила тяжести; 2) равнодействующая сил давления по вертикали; 3) равнодействующая сил вязкого трения на боковые поверхности выделенного элемента, и обусловленная градиентом скорости жидкости в направлении оси 0y.

Сила тяжести равна

где g_x – проекция ускорения свободного падения на ось 0х, r – плотность жидкости. Будем считать, что жидкость несжимаемая, т.е. r = const.

Равнодействующая сил давления. На верхней грани давление равно p,на нижней – (p + ). Площадь верхнего и нижнего граней dS = dy dz, следовательно, равнодействующая сил давления равна

p dy dz — (p + ) dy dz = — dy dz = — . (28)

Равнодействующая сил вязкого трения. При ламинарном течении жидкости сила вязкого трения возникает только на боковых (левом и правом) гранях выделенного элемента жидкости. Напомним, закон касательной силы вязкого трения на единицу площади контакта (закон Ньютона) имеет вид:

F_t =h , (29)

где h – коэффициент вязкости (или просто – вязкость), единицей вязкости служит паскаль×секунда (Па×с).

Если на левой боковой грани вязкое трение равно F_t , то на правой грани – (F_t + ). Так как скорость жидкости растет слева направо, то сила трения на левой грани площадью dS = dx dz направлена вверх, а на правой той же площади – вниз. Равнодействующая сил трения равна:

(F_t + ) dx dz – F_t dx dz = dy dz = .

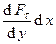
Воспользовавшись законом силы вязкого трения (29), получим при h = const:

= h dV . (30)

Если проекция скорости v_x изменяется по всем направлениям, т.е. проекция скорости v_x имеет градиент по всем направлениям, то равнодействующая вязкого трения в направлении оси 0х примет вид:

h 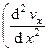+ + dV или hÑ 2 v_x dV . (31)

Итак, проекция результирующей силы R, действующей на выделенный элемент массой dm и объемом dV, на ось 0х примет вид:

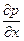
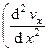
R_x = [r g_x — + h + + ] dV.

С другой стороны

dma_x = r dV = r + + + dV,

т.е. полное изменение скорости определяется: 1) локальной составляющей – изменением скорости во времени в данной точке пространства и 2) изменением в пространстве вследствие течения жидкости – конвективной составляющей + + . Итак:

r dV = r + + + dV.

Теперь можно записать второй закон динамики в развернутом виде:

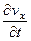
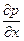
r + r + + = r g_x — + h + + . (32)

Дифференциальное уравнение (32), описывающее динамику движения вязкой несжимаемой жидкости (r = const), называется уравнением Навье-Стокса. Уравнение Навье-Стокса для проекций на оси 0y и 0z имеют аналогичный вид:

r + r + + = r g_y — + h + + ; (32 * )

r + r + + = r g_z — + h + + . (32 ** )

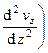
Заметим, уравнение Навье-Стокса справедливо как для ламинарного, так и турбулентного потока жидкости.

4.2.5. Уравнение непрерывности (сплошности)

Выделим в потоке жидкости мысленный неподвижный элементарный кубик с ребрами dx, dy, dz (рис. 4-9) и определим массу жидкости, протекающей через этот кубик за время dt.

В направлении оси 0x через левую грань с площадью dS = dydz втекает за время dt масса жидкости

а через правую грань той же площади вытекает масса

m_x2 = dy dz.

Имеем: dm_x = m_x2 — m_x1 = dx dy dz dt.

Аналогично по остальным осям:

dm_y = m_y2 — m_y1 = dx dy dz dt;

dm_z = m_z2 — m_z1 = 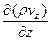dx dy dz dt.

Полное изменение массы жидкости в выделенном объеме dV = dx dy dz равно

dm = dm_x + dm_y + dm_z = + + dV dt.

Ясно, что изменение массы жидкости в выделенном объеме с течением времени может быть обусловлено только изменением плотности жидкости со временем. Следовательно, имеем:

+ + dV dt = — dV (33)

Знак минус в (33) указывает, что если dm > 0 (т.е. из объема dV вытекает большая масса жидкости, чем втекает), то 0, т.е. когда плотность жидкости в выделенном объеме увеличивается.

Уравнение (33) можно записать в виде:

+ + + = 0 (34)

Дифференциальное уравнение (34) и есть уравнение непрерывности (уравнение сплошности) в общем виде. Если плотность жидкости постоянна, (r = const) то уравнение непрерывности (34) примет вид

+ + = 0.

4.2.6. Условия однозначности математического описания

теплоотдачи (краевые условия). Подобие явлений

Процесс теплоотдачи математически описываются рассмотренными выше дифференциальными уравнениями: уравнением теплоотдачи; уравнением теплопроводности; уравнением динамики движения жидкости (газа); уравнением непрерывности. Применение этих уравнений к расчету конкретного процесса теплоотдачи требует введения в структуру уравнений частных особенностей этого процесса. Эти частные особенности называются условиями однозначности или краевыми условиями решения частной задачи. К этим условиям относятся:

1) геометрические условия, которые характеризуют размеры и форму, например, диаметр и длина, гладкость или шероховатость стенок канала протекания жидкости и т.п.;

2) физические константы, характеризующие свойства среды, например, плотность, вязкость, коэффициент теплопроводности и т.д.;

3) граничные условия протекания процесса на границах раздела сред, например, условие нулевой скорости жидкости в пристеночном вязком слое трубы; 4) временные условия, например, стационарность или нестационарность физических констант.

Процесс теплоотдачи – сложный процесс, и аналитическое решение системы дифференциальных уравнений возможно для ограниченного числа весьма упрощенных задач, т.к. особенности реального процесса теплоотдачи зависит от очень большого числа разного рода переменных величин, которые, к тому же, взаимосвязаны. В этой связи эксперимент приобретает решающее значение для анализа и расчета реальных процессов теплопроводности. Сам по себе эксперимент предварительно проводится на модельных объектах. Результаты эксперимента на модели выражают в форме определенного критерия подобия. Примером такого критерия подобия является число Рейнольдса. Эти критериальные оценки далее переносятся на объекты, подобные модельному объекту.

Методология теории подобия основывается на трех утверждениях (трех теоремах подобия):

1) подобные явления имеют одинаковые критерии подобия (Бертран Ж.). В модельном эксперименте измеряют те величины, которые содержатся в критерии;

2) уравнения, описывающие процесс, могут быть представлены в виде зависимости между критериями подобия, определяющими процесс (Федерман А., Букингем Дж.). Результаты опыта представляют в виде критериальных уравнений;

3) подобны те явления, краевые условия которых подобны и для которых критерии подобия, составленных из краевых условий, равны (Кирпичев М.В., Гухман А.А.). Это утверждение устанавливает признак подобия процессов в модельном и рабочем объектах.

Опишем некоторые критерии подобия. Все критерии представляют собой отношения одноименных величин и, следовательно, являются безразмерными величинами.

Число Эйлера Eu – это соотношение между перепадом силы давления в потоке F_p = Dpl 2 и поступательной силой инерции F_i = ma = rl 3 :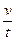

Eu = = = .

Число Эйлера характеризует соотношение между перепадом статического давления и динамическим давлением в потоке.

Число Рейнольдса Re определяет связь в потоке между поступательной силой инерции F_i = m 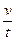и силой вязкого трения Ньютона F_h = h l 2 :

Re = = .

Число Рейнольдса характеризует гидродинамический режим вынужденного движения жидкости (газа).

Критерии теплового подобия получают из уравнений передачи тепла. Число Фурье Fo – отношение тепла, передаваемого теплопроводностью Q_l = l l 2 t и поступающим в тело массой m теплом Q = rl 3 cDT:

Fo = = = , где а – температуропроводность.

Число Фурье характеризует нестационарные процессы распространения тепла, определяемое скоростью изменения температурного поля, размерами тела, температуропроводностью.

Число Нуссельта Nu – отношение тепла передаваемого в процессе теплоотдачи Q_a = aDTl 2 t к теплу в процессе теплопроводности Q_l = l l 2 t:

Nu = .

Число Нуссельта характеризует интенсивность теплообмена на границе твердое тело (стенка) – жидкость.

Приложение:формулы и теоремы векторного исчисления

Векторные величины в тексте обозначены прямым полужирным шрифтом, скалярные – курсивом. Например, b – вектор, b – скаляр. Скалярное произведение векторов a и b записывается как(ab). Векторное произведение обозначено заключением сомножителей в квадратные скобки через запятую. Например, векторное произведение векторов a и b записывается как[a, b].

1.1. Скалярное произведение векторов abназывается произведение модулей векторов на косинус угла между этими векторами:

Выражение скалярного произведения через компоненты векторов в декартовой системе координат:

где i, j, k – единичные орты, ii = jj= kk = 1, ij= jk = ki =0.

1.2. Векторное произведение двух векторов[a, b]. В результате векторного произведения векторовaи b получается новый вектор c: [a, b] = c. Модуль результата векторного произведения – модуль вектора с— по определению равен c = ab sin (a^b). В декартовой системе координат векторное произведение имеет вид

[a, b] = .

1.3. Смешанное (скалярно-векторное) произведение трех векторов а[bc]. Результатом такого произведения является скалярная величина:

Смешанное произведение допускает циклическую (стековую) перестановку векторов:

По своему геометрическому смыслу смешанное произведение равно объему параллелепипеда, построенного на векторах а, bиc.

1.4. Двойное векторное произведение[а,[bc]]:

Здесь вначале выполняются скалярные произведения, стоящие в скобах (т.е. скалярные произведения acи ab), и только затем вектораb и c умножаются на соответствующие результаты скалярного произведения. Компоненты результата двойного векторного произведения имеют вид:

При проведении циклической перестановки в двойном векторном произведении получаются три разных вектора, сумма которых равна нулю:

2.1. Векторный оператор набла Ñ (оператор Гамильтона) как символический вектор:

Ñ = + + .

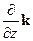
2.2. Градиент скалярной функции (скалярного поля) j(x, y, z) – это вектор, направленный в сторону быстрейшего увеличения j и равный производной по этому направлению. В координатном представлении градиент имеет вид:

gradj = Ñj (в развернутом виде Ñj = + + ).

2.3. Дивергенция некоторого вектора Eв данной точке пространства– это поток вектора Eиз бесконечно малого объема dV, находящегося в этой точке пространства. Объем dV — источник или сток вектора E. Дивергенция вектора E – скалярная величина и определяется скалярным произведением оператора набла на вектор E:

div Eº ÑE. В развернутом виде ÑE = + + .

2.4. Ротор некоторого вектора E –это вектор, порождающий циркуляцию некоторого другого вектора по бесконечно малому контуру. Например, в уравнении Максвелла rot Е= вектор является ротором, который порождает вихревой вектор – напряженность вихревого электрического поля Е. Ротор вектора E – векторная величина и кратко записывается векторным произведением оператора набла на вектор E:

В развернутом виде [Ñ, E] = i + j + k).

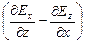
2.5.Некоторые векторные тождества.

1. Ñ(Ñj) = Ñ 2 j = , где j — скалярная функция.

3. Ñ[Ñ, E] = 0, где E — векторная функция.

2.6.Теоремы векторного анализа.

1. Теорема Гаусса-Остроградского. Здесь объем V ограничен замкнутой поверхностью S. Вектор dS в данной точке замкнутой поверхности направлен по внешней нормали к поверхности.

а) = или в форме = ;

б) = или в форме =

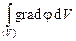
2. Теорема Стокса. Здесь замкнутый контур L ограничивает поверхность S, натянутая на контур. Вектор dl (как элемент контура L) по направлению совпадает с положительным обходом контура. Положительный обход контура связан с положительной нормалью к поверхности S правилом правого винта.

а) = или в форме = ;

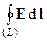
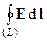
б) = или в форме = .

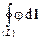
ЛИТЕРАТУРА

1. Савельев, И. В. Курс общей физики [Текст]: учеб. пособие. Кн.1., Кн.2., Кн.3, Кн.4 – М.: Наука, 2003.

2. Семенов, Н.А. Техническая электродинамика [Текст]: учеб. пособие для вузов. – М.: Связь, 1973. – 480 с.

3. Матвеев, А.Н. Электричество и магнетизм [Текст]: учеб. пособие для вузов. – М.: Высшая школа, 1983. – 463 с.

4. Алешин, Н.П. и др. Ультразвуковой контроль: учебное пособие/ под общ. ред. В.В. Клюева – М.: Изд. Дом «Спектр», 2011. – 224 с., ил.

5. Будадин, О.Н. и др. Тепловой контроль: учебное пособие/ под общ. ред. В.В. Клюева – М.: Изд. Дом «Спектр», 2011. – 176 с., ил.

Содержание

1. ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ И ВОЛН……………………………….7

1.1. Основные положения теории колебаний осцилляторов………………7

1.1.1. Уравнения колебаний гармонического осциллятора…………….7

1.1.2. Методы (способы) представления колебаний……………………10

1.1.3. Динамика гармонического осциллятора…………………………12

1.1.4. Динамика затухающих колебаний………………………………..15

1.1.5. Динамика вынужденных колебаний. Импеданс колебательной

1.1.6. Импеданс и фазовые соотношения между смещением и

вынуждающей силой. Резонанс смещения……………………….21

1.1.7. Импеданс и фазовые соотношения между скоростью и

вынуждающей силой. Резонанс скорости………………………..23

1.1.8. Устойчивость амплитуды вынужденных колебаний……………24

1.1.9. Добротность осциллятора…………………………………………26

1.1.10. Добротность и резонансная кривая поглощения

1.2. Исходные положения теории гармонических волн…………………….29

1.2.1. Волновое уравнение, описывающее бегущую волну в струне.

Фазовая скорость волны. …………………………………………29

1.2.2. Стоячие волны на струне………………………………………….33

1.2.3. Импеданс среды (на примере струны)…………………………….36

1.2.4. Отражение и прохождение волны на границе двух сред

с различными импедансами. Согласование импедансов………. 37

1.2.6. Затухание реальных волн в среде…………………………………41

2.1. Волновое уравнение плоской волны в газе и жидкости………………..42

2.2. Скорость акустической волны в твердом теле………………………….46

2.3. Поле плоского излучателя ультразвуковой волны……………………..47

3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ……………………………………………..48

3.1. Электростатическое поле…………………………………………………48

3.1.1. Объекты электростатики…………………………………………..48

3.1.2. Закон Кулона. Напряженность электростатического поля и

интегральная теорема Гаусса……………………………………..49

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 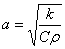— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Дифференциальное уравнение конвективного теплообмена

Для вывода дифференциального уравнения конвективного теплообмена в установившемся потоке жидкости (газа) выделяют элементарный параллелепипед с гранями dx, dy, dz (рис. 7.2) и составляют для него тепловой баланс, приняв физические параметры λ, с_р и ρ постоянными. Скорости движения жидкости в направлении осей x, y и z, соответственно – w_x, w_y и w_z. Температура жидкости t изменяется вдоль граней параллелепипеда. Теплоперенос в жидкости осуществляется путем конвекции и теплопроводности. Все подведенное к параллелепипеду тепло затрачивается только на изменение его энтальпии.

Количество тепла, которое вводится жидкостью путем конвекции по направлению оси х через грань dydz за время dτ,

.

За это же время через противоположную грань параллелепипеда путем конвекции жидкостью выводится количество тепла

,

.

Разность между количествами введенного и выведенного тепла в направлении оси х за время dτ составит:

.

Аналогично в направлении осей y и z

;

.

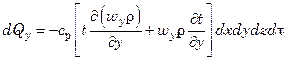
Полная разность между количествами введенного и выведенного путем конвекции тепла в объеме параллелепипеда за время dτ

.

На основании уравнения неразрывности потока (1.34)

.

Тогда конвективная составляющая теплового потока

,

где – объем параллелепипеда.

Количество тепла, которое вводится в параллелепипед жидкостью путем теплопроводности за время dτ, в соответствии с уравнением (7.21)

.

Суммарное количество тепла, подведенное конвекцией и теплопроводностью

Это тепло dQ, согласно первому началу термодинамики, равно изменению энтальпии жидкости в объеме параллелепипеда

.

.

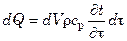
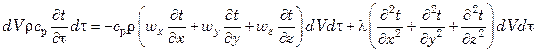
В результате простейших преобразований последнего равенства, получим

,

, (7.66)

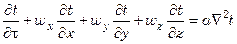
где – коэффициент температуропроводности.

Полученное уравнение (7.66) является дифференциальным уравнением конвективного теплообмена, или уравнением Фурье-Кирхгофа. Оно выражает в наиболее общем виде распределение температур в движущемся потоке жидкости (газа).

Для твердых тел w_x = w_y = w_z = 0 и уравнение (7.66) превращается в дифференциальное уравнение теплопроводности (7.23).

При установившемся процессе теплообмена , тогда уравнение конвективного теплообмена для этого случая

. (7.67)

Ввиду сложности уравнения (7.66) для практического использования его подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия. Для этого, с целью более полного описания конвективного переноса тепла, дифференциальное уравнение Фурье-Кирхгофа дополняется граничными условиями, вытекающими из закона теплообмена на границе твердого тела и окружающей его среды.

Тепловое подобие

На практике процессы теплообмена осуществляются с помощью потоков разнообразных жидкостей и газов при различных режимах их движения в аппаратах различной геометрической формы и размеров. Однако условия подобия во всех случаях одинаковы и сводятся к подобию геометрических параметров, полей скоростей и температуры, а также физических констант. При этом должно соблюдаться подобие переноса тепла, как в пограничном слое, так и в ядре потока жидкости (газа).

Подобие переноса тепла в пограничном слое можно установить из краевых условий теплообмена на границе твердое тело – жидкость (газ), воспользовавшись зависимостью (7.64):

.

Применив тот же метод подобного преобразования уравнений, что и при выводе критериев гидродинамического подобия (см. раздел 1.3.6), разделим правую часть последнего равенства на левую:

.

Заменив на характерный (определяющий) геометрический размер , получим безразмерный комплекс величин, называемый критерием Нуссельта:

. (7.68)

Критерий Нуссельта характеризует теплоперенос через пограничный слой в форме соотношения количества тепла, передаваемого конвекцией, и теплопроводностью.

Аналогом критерия Нуссельта при нестационарном теплообмене между твердым телом и жидкостью или газом является критерий Био:

, (7.69)

где – коэффициент теплопроводности твердого тела.

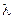
Условия подобия в ядре потока определяются из уравнения Фурье-Кирхгофа (7.66). Для одномерного движения потока жидкости его можно представить в виде

. (7.70)

Поделив члены левой части на правую часть, отбросив знаки математических операторов и заменив величины и на характерный геометрический размер и осредненную скорость соответственно, получим

;

.

Полученный комплекс обычно для удобства заменяют обратной величиной , которая выражает необходимое условие подобия неустановившихся процессов теплообмена. Этот безразмерный комплекс получил название критерия Фурье:

. (7.71)

Комплекс является мерой соотношения между теплом, переносимым конвекцией и теплопроводностью при конвективном теплообмене, и носит название критерия Пекле:

. (7.72)

Необходимым условием теплового подобия являются предшествующие ему гидродинамическое и геометрическое подобия. Гидродинамическое подобие определяется критериями гомохронности Но, Рейнольдса Re и Фруда Fr, а геометрическое – постоянством отношений основных геометрических размеров поверхности (стенки) к некоторому характерному размеру L. В качестве характерного линейного размера для трубных поверхностей, которые часто используются в качестве теплопередающих, принимают диаметр трубы L = d, иногда – длину трубы L = l, радиус кривизны изогнутой трубы L = R и т.д. В результате критериальное уравнение конвективного теплообмена выражается функцией вида

, (7.73)

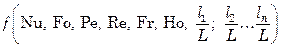
где – симплексы геометрического подобия.

Равенство критериев Нуссельта является следствием подобия геометрических и физических характеристик, а также подобия полей скоростей и температур. Поэтому Nu не является определяющим. В связи с этим обобщенную зависимость, описывающую кинетику переноса тепла в движущихся средах, представляют в виде

. (7.74)

Критерий Пекле обычно представляют в виде двух безразмерных комплексов

,

где – критерий Прандтля, характеризующий физические свойства теплоносителя (жидкости или газа).

По физическому смыслу критерий Pr определяет соотношение полей скоростей и температур в потоке. Для капельных жидкостей он зависит от температуры (с повышением температуры увеличивается), а его численные значения лежат в пределах 3 ÷ 300. Для газов критерий Прандтля не зависит ни от температуры, ни от давления, являясь постоянной величиной для газов одинаковой атомности (для одноатомных газов Pr = 0,67; для двухатомных Pr = 0,72; для трехатомных Pr = 0,8; для четырехатомных и более Pr = 1).

С введением критерия Прандтля уравнение (7.74) принимает вид:

. (7.75)

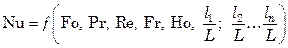
При установившихся тепловых процессах и одинаковой геометрической форме потоков из уравнения (7.75) исключаются критерии Fo и Ho, содержащие время, и геометрические симплексы, тогда

. (7.76)

При рассмотрении конкретных задач теплообмена уравнение (7.76) может быть видоизменено.

Так, при вынужденном движении, когда влияние сил тяжести на гидродинамику потока пренебрежительно мало, критерием Фруда можно пренебречь и критерий Нуссельта будет являться функцией лишь двух критериев:

. (7.77)

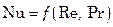
При свободном движении жидкости (в условиях естественной конвекции) из критериального уравнения исключают критерий Рейнольдса:

. (7.78)

Ввиду сложности определения скорости при естественной конвекции, входящей в критерий Фруда, последний заменяют производным критерием Архимеда, характеризующим естественную конвекцию, обусловленную разностью плотностей жидкости (газа) в различных точках потока:

,

где ρ и ρ₀ – плотности холодной и нагретой жидкости (газа).

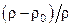
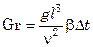
Поскольку в тепловых процессах разность плотностей в различных точках системы обусловливается разностью температур Δt нагретой и холодной жидкости, комплекс в критерии Архимеда целесообразно выразить через произведение bΔt (b – температурный коэффициент объемного расширения). Полученный новый критерий является критерием Грасгофа:

. (7.79)

Таким образом, критерий Gr представляет собой определяющий критерий теплового подобия при естественной конвекции, когда движение жидкости целиком обусловлено самим процессом теплообмена, а уравнение конвективного теплообмена для этого случая

. (7.80)

Для газов при Pr ≈ 1 уравнение (7.79) превращается в функциональную зависимость критерия Нуссельта от критерия Грасгофа.

Помимо приведенных критериев теплового подобия в литературе часто встречаются производные критерии, составленные из указанных выше:

критерий Стантона , (7.81)

который отражает соотношение количества тепла, передаваемого конвекцией, и тепла, переносимого движущимся потоком;

критерий Релея ; (7.82)

критерий Грэтца 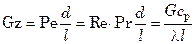, (7.83)

(G – массовый расход жидкости) характеризует конвективный теплоперенос при ламинарном режиме.

.

В соответствии с полученными критериальными уравнениями обрабатываются опытные данные по переносу тепла конвекцией и представляются в виде степенных уравнений. Например, уравнение (7.77) – в виде ; уравнение (7.79) – в виде и т.д.

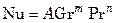
При решении практических задач по найденному из соответствующего критериального уравнения значению критерия Нуссельта определяют коэффициент теплоотдачи:

.

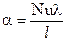
Критериальные зависимости в виде степенных уравнений, как уже указывалось, решают чисто эмпирически и применимы они лишь в тех пределах изменения аргумента, в которых подтверждены опытом. Поэтому области их надежного применения ограничены пределами, указываемыми в каждом отдельном случае. Ограничения эти, в основном, связаны с характером и режимом движения потока теплоносителя, его геометрической формой и размерами, изменением агрегатного состояния.