Вывод уравнения нормали к плоской кривой

Лекция Плоские кривые. Способы задания плоской кривой.Длина плоской кривой. Касательная и нормаль к кривой. Кривизна кривой. Эволюта и эвольвента

III . ПЛОСКИЕ КРИВЫЕ.

1. Способы задания плоских кривых.

2. Уравнения касательной и нормали.

3. Формулы для нахождения единичного вектора нормали и кривизны.

4. Уравнение эволюты.

3.1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОЙ КРИВОЙ.

Кривая, у которой кручение в каждой точке равно нулю, располагается в плоскости и поэтому называется плоской. В качестве такой плоскости выбирают плоскость хОу.

Геометрию плоских кривых можно получить как частный случай геометрии кривых в пространстве, но при таком подходе могут ускользнуть многие своеобразные их особенности. В связи с этим теория плоских кривых строится независимо от теории кривых в пространстве.

Кривую на плоскости можно задать уравнениями различных видов, наиболее распространенными из которых являются:

а) векторное уравнение , (3.1)

б) векторно-параметрическое уравнение (3.2)

в) координатно-параметрические уравнения

г) уравнение в несимметричной форме

или (3.5)

Заметим, что присоединив к уравнению (3.4) тождество х=х , получим параметрические уравнения х=х, y = f ( x ). Они отличаются от уравнений (3.3) тем, что за параметр принята абсцисса точка кривой.

В частности, если какая-либо точка кривой не является особой (т.е. отлична от нуля по крайней мере одна из производных в этой точке), то в ее окрестности уравнение (3.6) можно разрешить или относительно у (при ), и тогда получим уравнение (3.4), или относительно х (при ), тогда получим уравнение (3.5).

3.2 ДЛИНА ПЛОСКОЙ КРИВОЙ.

Длиной кривой называется верхняя грань всех возможных ломаных, вписанных в данную кривую. В частности, если кривая задана векторно-параметрическим уравнением и функция непрерывна вместе со своей производной на , то она спрямляема.

а) Длина кривой в прямоугольных координатах .

Если плоская кривая задана уравнением , где функция непрерывна вместе со своей производной на [ a , b ], то она спрямляема и ее длина выражается формулой

(3.7)

Если кривая задана параметрическими уравнениями и функции непрерывно дифференцируемы на [ T ₁ , T ₂ ], то ее длина выражается формулой:

(3.8)

б) Длина кривой в полярных координатах.

Если кривая задана в полярных координатах уравнением и функция непрерывна вместе со своей производной на , то ее длина выражается формулой

(3.9)

Пример 3.1 Найти длину полукубической параболы ay 2 = x 3 , a >0 от х =0 до х=5а .

Решение: Из уравнений кривой следует, что полукубическая парабола симметрична относительно оси абсцисс (замена у= ‑у не изменяет уравнения) и расположена в правой полуплоскости координатной полуплоскости хОу ( х не может быть отрицательным). Вычислим длину одной ветви кривой ОА.

Из уравнения кривой находим .

По формуле (3.7) получим:

Длина кривой равна S =670 а /27.

Пример 3.2 Вычислить длину кардиоиды .

Решение: Однозначная ветвь функции r соответствует изменению параметра в промежутке , при этом кривая симметрична относительно полярной оси. При изменении от 0 до полярный радиус r опишет половину кривой. Половину длины кардиоиды найдем, используя формулу (3.9):

Длина всей кардиоиды S =8 a .

3.3 КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ.

Единичный вектор направленной касательной, как мы показали выше (1.7), находится как орт производной радиус-вектора: .

На практике иногда удобнее в качестве направляющего вектора касательной брать вектор (или любой ему коллинеарный вектор) и уравнение касательной в точке записать в виде:

(3.10)

или . (3.11)

В качестве направляющего вектора нормали можно взять единичный вектор главной нормали , или, что на практике гораздо проще, вектор , ортогональный вектору , тогда уравнение нормали будет иметь вид:

(3.12)

или . (3.13)

Если кривая задана уравнением в несимметричной форме (3.4), то касательная и нормаль соответственно имеют уравнения

(3.14)

(3.15)

г) Если кривая задана уравнением в симметричной форме (3.6), то касательная и нормаль соответственно имеют уравнения

(3.16)

(3.17)

Пример 3.3 Составить уравнение касательной и нормали к кривой y = x 3 -2 в точке А(2,3).

Решение: Используем уравнение касательной (3.14) и нормали для кривой, заданной в несимметричной форме. Запишем уравнение пучка прямых, проходящих через данную точку А(2,3): y -3= k ( x -2),

где k – угловой коэффициент прямой (в данном случае произвольный параметр). Для определения k , соответствующего касательной и нормали к кривой, найдем производную при х =2:

Следовательно, для касательной k =12, для нормали k = ‑ 1/12. Подставляя эти значения в уравнение пучка прямых, получим уравнение касательной

Пример 3.4 Составить уравнение касательной и нормали к декартовому листу х 3 +у 3 -3аху=0, а>0 (рис.9) в точке А ( 3а/2;3а/2 ).

Решение. Используем уравнения касательной (3.16) и нормали (3.17) для кривой заданной в симметричной форме. Записав исходное уравнение в виде F( x,y )=0 , найдем:

Подставляя значения производных в уравнение касательной

и нормали: ,

получим уравнение касательной у=3а-х , и уравнение нормали у=х .

3.4 КРИВИЗНА КРИВОЙ. ЭВОЛЮТА И ЭВОЛЬВЕНТА КРИВОЙ.

Если кривая задана уравнением у=у(х), то ее кривизна определяется по формуле:

(3.18)

В случае векторно-параметрического задания кривой

(3.19)

Радиус кривизны в данной точке:

(3.20)

Всякая прямая, проходящая через точку кривой и перпендикулярная касательной в этой точке, называется нормалью к кривой в данной точке. Вектор нормали к кривой, направленный в сторону центра кривизны и указывающий направление, в котором кривая в окрестности рассматриваемой точки отклоняется от своей касательной, называется вектором главной нормали. Множество центров кривизны кривой образуют ее эволюту. В случае векторно-параметрического задания кривой уравнение эволюты имеет вид (2.17): , и координаты центра кривизны определяются формулами:

, (3.21)

Если кривая задана уравнением y = f ( x ) , то

, (3.22)

Исходная кривая по отношению к своей эволюте называется эвольвентой.

Пример 3.5 Найти кривизну и радиус кривизны параболы у=х 2 в произвольной точке х.

Решение: Кривизну параболы найдем, подставляя в (3.18):

Эта величина принимает наибольшее значение при х =0, для которого k =2. Радиус кривизны связан с кривизной соотношением (3.20), поэтому

Наименьший радиус кривизны в точке (0,0).

Пример 3.6 Найти радиус кривизны и эволюту эллипса .

Решение: Представим уравнение эллипса в параметрическом виде:

Подставляя в формулы (3.19) и (3.20), получим

Уравнение эволюты найдем по формуле (3.21):

Таким образом, эволютой эллипса является астроида.

Касательная и нормаль к графику функции

Основные формулы

Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Определения

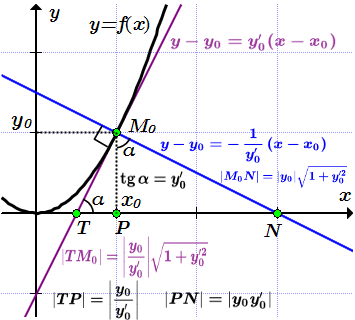
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

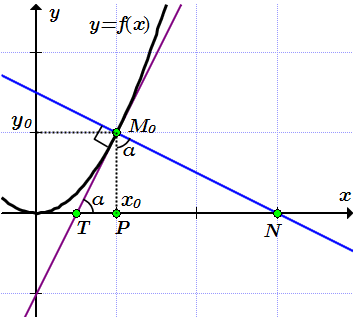
Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

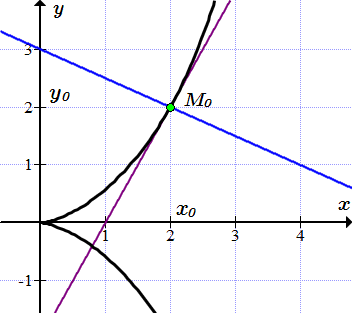
Касательная и нормаль к циссоиде в точке (2;2).

Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

Вывод уравнения нормали к графику функции

Вы будете перенаправлены на Автор24

Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.

Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ

В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:

Пользуясь полученным выводом, запишем уравнение нормали к графику функции:

$y – y_0 = — \frac<1> \cdot (x – x_0) \left(1\right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.

Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:

Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
Затем нужно определить производную.
Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
Все найденные значения подставляются в формулу $(1)$.

Напомним также как выглядит само уравнение касательной:

$y – y_0 = f’(x_0) \cdot (x – x_0)$.

Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.

Решение:

Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.

Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 \cdot 2= 4$.

Все полученные значения расставляем по своим местам в формулу $(1)$:

источники:

http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/

http://spravochnick.ru/matematika/vyvod_uravneniya_normali_k_grafiku_funkcii/