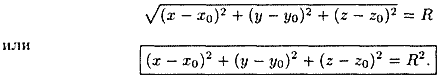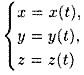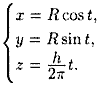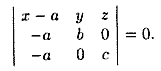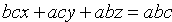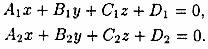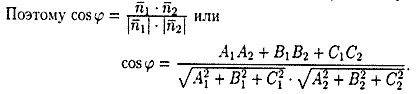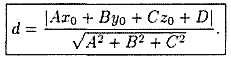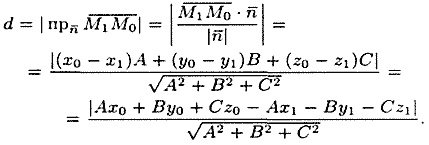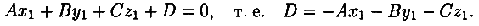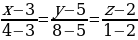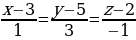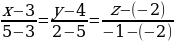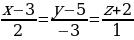Вывод уравнения сферы уравнения плоскости

Лекция № 10

Ссылки

Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ

12.1. Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О₁ есть геометрическое место всех точек пространства, находящихся от точки O₁ на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками простран­ства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего ко­ординаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называ­ются текущими координатами точек поверхности.

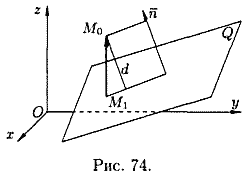
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M₁(x₁;y₁;z₁) на данной поверхности, достаточно подстав и ть координаты точки M₁ в уравнение поверхности вместо пере­менных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.

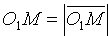
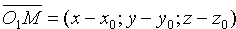
Найдем уравнение сферы радиуса R с центром в точке O₁(x₀;y₀;z₀). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O₁(x₀;y₀;z₀) равно радиусу R, т. е. O₁M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю­бой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο₁ совпадает с началом координат, то уравнение сферы принимает вид .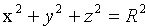

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

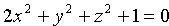
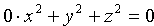
Так, уравнению не удовлетворяют никакие дей­ствительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).

Итак, поверхность в пространстве можно задать геометрически и ана­литически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве

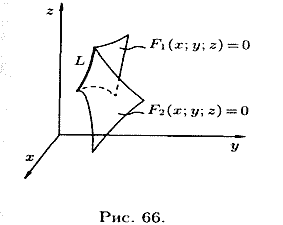
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, об­щих двум поверхностям.

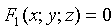
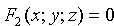
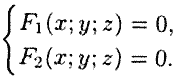
Если и — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

(12.1)

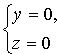
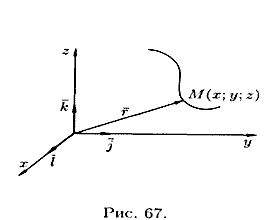
Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, есть уравнения оси Ох.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

(12.2)

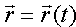
или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

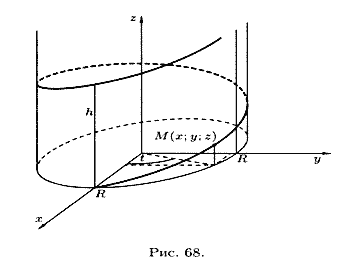
Например, параметрические уравнения винтовой линии имеют вид

Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

12.2. Уравнения плоскости в пространстве

Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

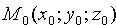
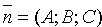
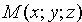
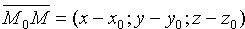
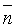
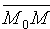
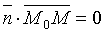
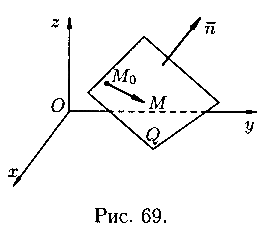
Пусть в пространстве Oxyz плоскость Q задана точкой и вектором , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку и составим вектор . При любом расположении точки Μ на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: , т. е.

(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).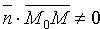

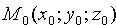
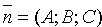
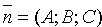
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку 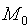. Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:

(12.4)

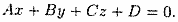
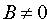
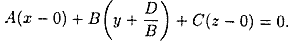
Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например , перепишем уравнение (12.4) в виде

(12.5)

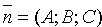
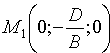
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором , проходящей через точку .

Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.

Частные случаи общего уравнения плоскости:

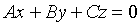
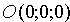
1. Если D = 0, то оно принимает вид . Этому уравнению удовлетворяет точка . Следовательно, в этом случае плос­кость проходит через начало координат.

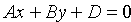
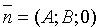
2. Если С = 0, то имеем уравнение . Нормальный вектор перпендикулярен оси Οz. Следовательно, плоскость параллельна оси Οz; если B = 0 — параллельна оси Оу, А = 0 — параллельна оси Ох.

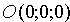
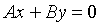
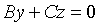
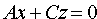
3. Если С = D = 0, то плоскость проходит через параллельно оси Οz, т. е. плоскость проходит через ось Οz. Аналогично, уравнениям и отвечают плоскости, проходящие соответственно через оси Ох и Оу.

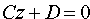
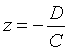
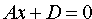
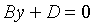
4. Если А = В = 0, то уравнение (12.4) принимает вид , т. е. Плоскость параллельна плоскости Оху. Аналогично, уравнениям и отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.

5. Если A = B = D = 0, то уравнение (12.4) примет вид 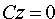, т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение плоскости Οxz; x = О — уравнение плоскости Oyz.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M₁(x₁;y₁;z₁), М₂(x₂;y₂;z₂) и М₃(х₃,y₃,z₃), не лежащие на одной прямой.

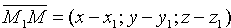
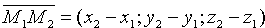
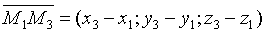
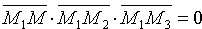
Возьмем на плоскости произвольную точку M(x;y;z) и составим век­торы , , . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарнос­ти трех векторов (их смешанное произведение равно нулю), получаем , т. е.

(12.6)

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках

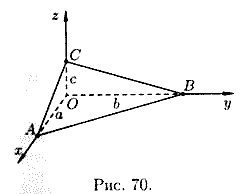
Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т. е. проходит через три точки A(a;0;0), B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

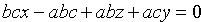
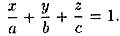
Раскрыв определитель, имеем , т. е. или

(12.7)

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора 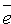, имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

Пусть ОК = p, а α, β, g — углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости Q проекция радиус-вектора на направление вектора всегда равно р: , т. е. или

(12.8)

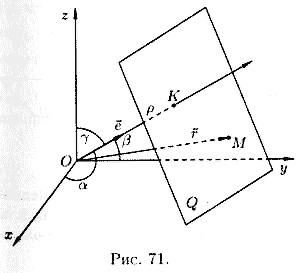
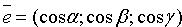
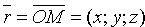
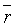
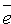
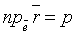
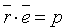
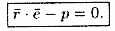
Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде

(12.9)

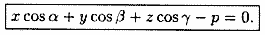
Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на норми­рующий множитель 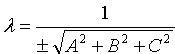, где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

12.3. Плоскость. Основные задачи

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть заданы две плоскости Q₁ и Q₂:

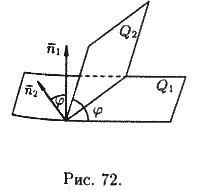
Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.

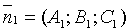
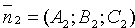
Угол j между нормальными векторами и плоскостей Q₁ и Q₂ равен одному из этих углов (см. рис. 72).

Для нахождения острого угла следует взять модуль правой части.

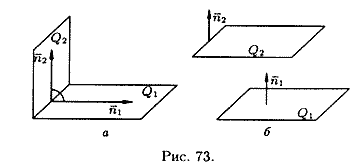
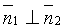
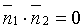
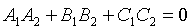
Если плоскости Q₁ и Q₂ перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. (и наоборот). Но тогда , т. е. . Полученное равенство есть условие перпендикулярности двух плоскостей Q₁ и Q₂.

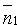
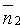
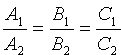
Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут параллельны и их нормали и (и наоборот). Но тогда, как известно координаты векторов пропорциональны: . Это и есть уcловиє параллельности двух плоскостей Q₁ и Q₂.

Расстояние от точки до плоскости

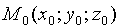
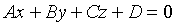
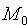
Пусть задана точка и плоскость Q своим уравнением . Расстояние d от точки до плоскости Q находится по формуле

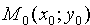
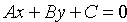
Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой .

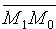
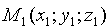
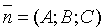
Расстояние d от точки M₀ до плоскости Q равно модулю проекции вектора , где — произвольная точка плоскости Q, на направление нормального вектора (см. рис. 74). Следовательно,

А так как точка 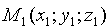принадлежит плоскости Q, то

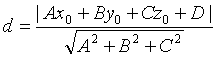
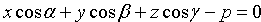
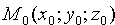
Поэтому . Отметим, что если плоскость Q задана уравнением , то расстояние от точки до плоскости Q может быть найдено по формуле

Уравнение прямой, плоскости и сферы

306 гр. Математика. Дистанционное обучение. Тема 1-3.

Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»

Тема 1: Уравнение прямой в пространстве.

З адание: записать конспект и выполнить самостоятельную работу.

Пример 1. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ: 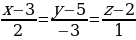Самостоятельная работа

Пример 1. Составить уравнение прямой, проходящей через две точки:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Пример 3. Составить уравнение прямой, проходящей через две точки:

Тема 2: Уравнение плоскости в пространстве

Задание: записать конспект и выполнить самостоятельную работу

П 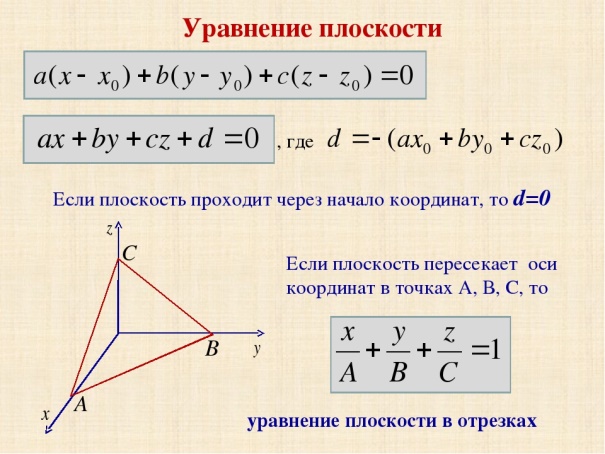ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.

Ответ: точка В (-1; 2; 7) принадлежит плоскости.

Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0

0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно

Ответ: точка Е(0; 4; -6) не принадлежит плоскости.

Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

Решение: Подставим координаты точки в уравнение и найдем D.

Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением

Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением

Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0

Решить задания №1, №2

О пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.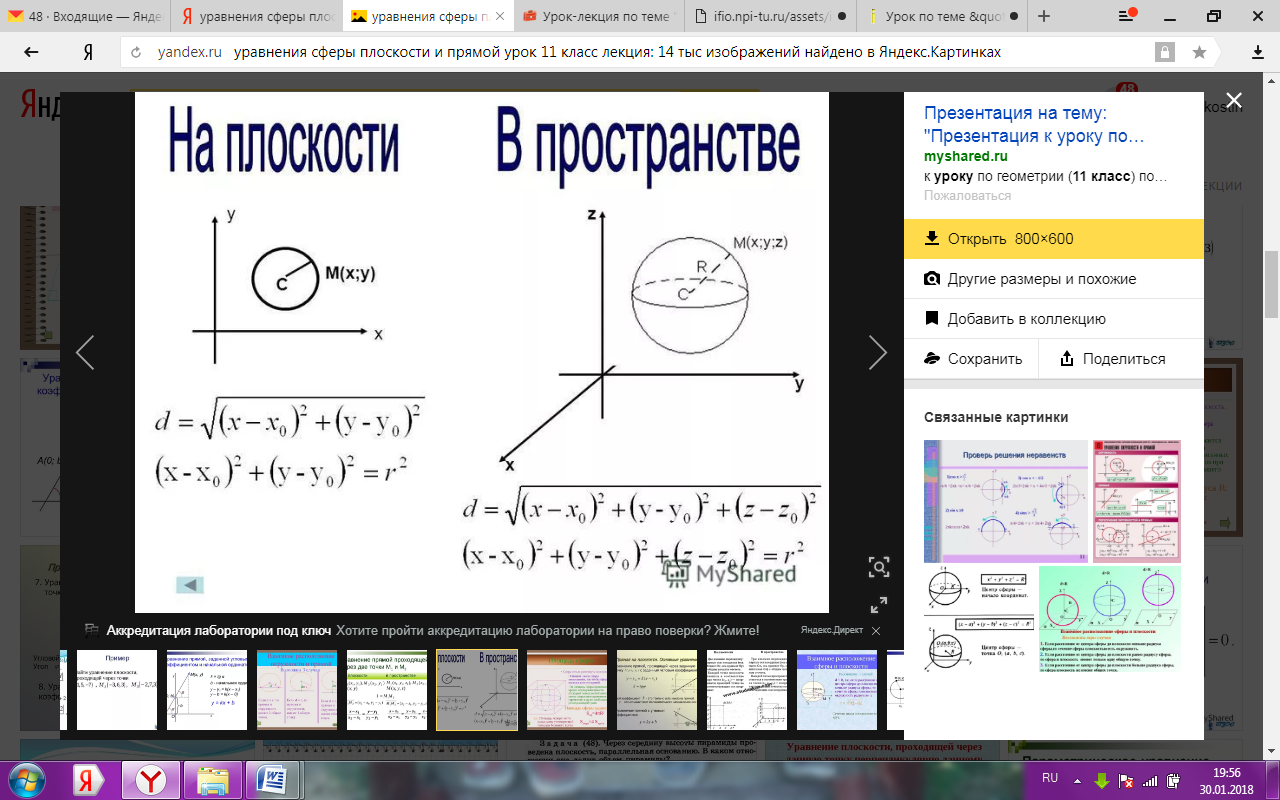

R – радиус сферы, т. О – центр сферы.

Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.

Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .

Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.

1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64

2)найдем радиус: R 2 =64, R=√64=8,

Ответ: О(6, -3, 4), R = 8.

Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6

Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.

Уравнения сферы, плоскости и прямой
презентация к уроку по геометрии (10, 11 класс)

Уравнения сферы, плоскости и прямой

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Понятие сферы и её элементов Уравнение сферы в заданной системе координат СФЕРА УРАВНЕНИЕ СФЕРЫ

Тело вращения — сфера

Определение сферы Элементы сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. т.О — центр сферы ОА – радиус сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы. ВС – диаметр сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы d=2r

? Какие из тел, изображенных на рисунках, являются сферой? 1 2 3 4 5 6

На плоскости В пространстве L М(х;у) х у L Сформулируйте определение линии L на плоскости Уравнение с двумя переменными х и у называется уравнением линии L , если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии Уравнение с тремя переменными х,у, z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности Х z Сформулируйте определение уравнения поверхности в пространстве Х у М(х;у; z ) •

На плоскости В пространстве М(х;у) х у х у z (х;у; z ) С

Частные случаи 1.Уравнение окружности с центром в т.О(0;0) и радиусом r 1.Уравнение сферы с центром в т.О(0;0;0) и радиусом R

Выбрать из предложенных уравнений – уравнение сферы: 1. 2. 3. 4. 5. 6. 7. 8. 1.Ур-е окружности 2.Ур-е сферы 3.Ур-е прямой 4.Ур-е сферы 5.Ур-е параболы 6.Ур-е сферы 7.Ур-е сферы 8. ?

В данных уравнениях определите координаты центра сферы и радиус 1. 2. 3. 4.

Составьте уравнение сферы по следующим данным центра и радиуса сферы: Дано: С(-2;8;1); R =11 Дано: А(3;-2;0); R =0,7 Дано: О(0;0;0); R =1 Проверяем ответы:

Задача Определить принадлежит ли т.А сфере, заданной уравнением если: а) т.А(5;-2;6) б) т.А(-5;2;6) Решение: Равенство верное , следовательно А(5;-2;6) принадлежит сфере Равенство неверное , следовательно А(5;-2;6) не принадлежит сфере

Уравнение плоскости и прямой

совпадают, если существует такое число k , что параллельны, если существует такое число k , что В остальных случаях плоскости пересекаются.

Если известна какая-нибудь точка плоскости M 0 и какой-нибудь вектор нормали к ней , то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: n (A;B;C) M 0

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку M( x ; y ; z ) . Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. Вектор задан по условию. Координаты вектора найдём по формуле : Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Используем формулу A ( x — x 0 )+B(y-y 0 )+C(z-z 0 )=0

Уравнение прямой в пространстве Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве Прямую, проходящую через точку A 0 ( x 0 , y 0 , z 0 ) с направляющим вектором ( a , b , c ) можно задавать параметрическими уравнениями В случае, если прямая в пространстве задается двумя точками A 1 ( x 1 , y 1 , z 1 ), A 2 ( x 2 , y 2 , z 2 ), то, выбирая в качестве направляющего векто­ра вектор ( x 2 — x 1 , y 2 — y 1 , z 2 — z 1 ) и в качестве точки А 0 точку А 1 , получим следующие уравнения

Упражнение 1 Какими уравнениями задаются координатные прямые? Ответ: Ось Ox Ось O y Ось O z

Упражнение 2 Напишите параметрические уравнения прямой, проходящей через точку А (1,-2,3) с направляющим вектором, имеющим координаты (2,3,-1). Ответ:

Упражнение 3 Напишите параметрические уравнения прямой, проходящей через точки А 1 (-2,1,-3), А 2 (5,4,6). Ответ:

Упражнение 4 Напишите параметрические уравнения прямой, проходящей через точку M (1,2,-3) и перпендикулярную плоскости x + y + z + 1 = 0. Ответ:

Упражнение 5 В каком случае параметрические уравнения определяют перпендикулярные прямые? Ответ: Если выполняется равенство a 1 a 2 +b 1 b 2 +c 1 c 2 = 0 .

По теме: методические разработки, презентации и конспекты

Практическая работа «Построение углов между плоскостями, между прямой и плоскостью»

Практическая работа по геометрии ,10 класс. Хотя данную работу можно провести при подготовке к ЕГЭ по математике, при решении задач типа С2. Работа содержит 8 заданий на построение угла между прямой и.

Тест по теме «Параллельность прямых и плоскостей. Перпендикулярность прямых в пространстве» (геометрия 10 класс)

Данный тест можно предложить учащимся как входной перед изучением темы «Многогранники».

Параллельность прямых и плоскостей. Параллельные прямые в пространстве

Урок-презентация по геометрии 10 класс.

Тесты по теме «Прямые в пространстве. Параллельность прямых, прямой и плоскости», «Перпендикулярность прямых, прямой и плоскости»

Тесты предназначены для проверки усвоенияследующих понятий и определений: взаимное расположение прямых в пространстве, определение скрещивающихся прямых, определение параллельных прямых, признак парал.

Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространств.

Расстояние от точки до плоскости, от прямой до плоскости

Материал для практической работы «Расстояние от точки до плоскости, от прямой до плоскости&quot.

Составление уравнений сферы, плоскости, прямой.

Составление уравнений сферы, плоскости, прямой.