Вывод уравнения теплопроводности для стержня и пластины

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 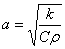— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Электронная библиотека

Рассмотрим однородный стержень (под стержнем в механике понимается тело с одним превалирующим линейным размером, например, столб можно рассматривать как стержень с переменным сечением) постоянного поперечного сечения S и длины l, теплоизолированный с боков, ось которого примем за ось Ох (рис. 4.3). Обозначим через U(x,t) температуру стержня в сечении с абсциссой х в момент времени t (предполагается, что во всех точках любого поперечного сечения стержня температура одна и та же.

Пусть – плотность стержня, – его удельная теплоемкость (это количество калорий, которое необходимо, чтобы единицу массы стержня нагреть на 1 ºС), – коэффициент теплопроводности (он представляет собой количество тепла в калориях, которое будет протекать за единицу времени через сечение стержня, если температура стержня падает на 1 ºС при перемещении вдоль стержня на единицу длины), – интенсивность теплового источника, находящегося в сечении х для момента t, отнесенная к единице массы и единице времени (т.е. количество тепла, создаваемого этим источником тепла за единицу времени и приходящегося на единицу массы; например, лампочку включенную в помещении, аппаратуру, работающую на космическом корабле и др. можно рассматривать как источники тепла;). Температуру же U(x, 0) стержня в начальный момент времени мы считаем известной и обозначим её через :

Тепловой режим на концах стержня может быть весьма разнообразен, т.е. температура может быть и постоянной, и изменяться, например, по законам: и др.). Мы рассмотрим два случая:

1) концы стержня поддерживаются при постоянной нулевой температуре:

2) концы стержня находятся в той же теплоизолирующей оболочке, что и весь стержень. Это означает, что через концы не происходит протекание тепла.

Рассмотрим сечение х нашего стержня и найдем, какое количество Q тепла протечет (слева направо) через это сечение за элементарный промежуток времени . В момент t температура стержня в точке х будет равна . Возьмем отличную от точки х точку x + dx стержня (пусть для определенности dx > 0) согласно закону Фурье количество тепла, протекающего в направлении оси Ох за бесконечно малый промежуток времени dt через сечение S с абсциссой х, будет:

где k – коэффициент теплопроводности ( представляет здесь величину градиента температуры U). Во формуле (4.37) стоит знак минус, так как при , т.е. при росте U вместе с х, поток тепла направлен в противоположную сторону, и наоборот).

Составим тепловой баланс для элемента , заключенную между бесконечно близкими сечениями х и x + dx. Предположим для определенности, что U возрастает в направлении Ох.

Тогда через сечение с абсциссой х тепло выходит, а через сечение с абсциссой x + dx входит. Пусть dQ есть количество тепла, накопленное нашим элементом за время dt. Тогда количество тепла, созданное за dt источниками тепла в элементе равно:

Используя формулу (4.37) будем иметь:

Применяя формулу Лагранжа из дифференциального исчисления с точностью до бесконечно малых высшего порядка малости, получим:

Следовательно, формула (4.39) примет вид:

С другой стороны, есть скорость изменения температуры элемента , и поэтому представляет собой изменение его температуры. Так как масса элемента равна , то накопленное при этом количество тепла будет:

Итак, сравнивая (4.41) и (4.40), после сокращения получим:

или, обозначая (величина а называется коэффициентом температуропроводности), окончательно получим дифференциальное уравнение, описывающее распределение температуры U(x,t) в стержне и носит название уравнения теплопроводности:

Если источники тепла отсутствуют, то уравнение (4.43) принимает вид уравнения свободного теплообмена в стержне:

Аналогичным образом можно вывести уравнения для распространения температуры в пластине:

где – оператор Лапласа (см. разд. 1.4.6).

Вывод: уравнение теплопроводности есть уравнение с частными производными второго порядка, параболического типа, так как ; в процессе вывода уравнения теплопроводности мы пришли к двум математическим задачам:

1) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям (4.36).

2) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям:

т.е. когда концы стержня теплоизолированы (количество тепла, протекающее через них, равно нулю).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Вывод уравнения теплопроводности стержня. Вывод уравнения продольных колебаний стержня. Вывод уравнения малых поперечных колебаний струны. Граничные условия для уравнения колебаний струны. Граничные условия для уравнения колебаний стержня. Граничные условия для уравнения теплопроводности стержня. Уравнения теплопроводности и колебаний и интуиция. Смешанная задача и другие задачи в частных производных

Страницы работы

Содержание работы

1. Введение в предмет ММФ

2.Вывод уравнения теплопроводности стержня 3. .Вывод уравнения продольных колебаний стержня

4. .Вывод уравнения малых поперечных колебаний струны 5.Граничные условия для уравнения колебаний струны

6.Г раничные условия для уравнения колебаний стержня 7. Граничные условия для уравнения теплопроводности стержня 8.Уравнения теплопроводности и колебаний и интуиция 9.Смешаная задача и другие задачи в частных производных

10.Простейшие статические задачи с (ГУ )12 11.Плотность точечной силы и бета ф-ция Дирака-Кирхгофа 12.Статическая задача с точечной силой и ГУ

13. Статическая задача с непрерывно распределённой силой и ГУ11 14.Функция Грина статической задачи с распределённой силой и (ГУ)11 15.Функция свойства Грина статической кравеой задачи с (ГУ)11

16.Простейшие статические задачи для струны в упругой среде 17.Различные формы записи общего решения одного обыкновенного дифференциального решения 18.Статическая задача для струны в упругой среде с точечной силой и (ГУ)11 19.Статическая задача для струны ы упругой среде с непрерывно аспеределённой силой и (ГУ)11.Метод вариации постоянных 20.Функция Грина статической задачи для струны в упругой среде и её свойства 21.Метод разделения переменных 22.Задача Штурма-Леувилля с ГУ11

23.Ортонормированность собственных функций задач Штурама Леувилля 24.Решение задачи Штурма-Леувилля с периодическими ГУ в экспонициальной форме 25.Свойства СФ задачи Штурма-Леувилля с периодическими ГУ 26.Задача Штурама-Лиувилля и смешанная задача 27.Смешанная задача и проблема разложения функции в ряд Фурье 28. Проблема разложения функции в ряд Фурье и размазанная бета функции 29.Явный вид размазаной бета функции,Теорема о поточечной сходимости 30.Экспонициальные и тригонометрические ряды Фурье 31.Синус-ряды Фурье и косинус-ряды Фурье 32.Смешанная задача и вспомогательная задача Коши 33.Решение вспомогательной задачи Коши для УТ 34.Вспомогательная задача Коши для УК 35.Решение проблемы неоднородных ГУ11 для уравнений теплопроводности и колебаний 36. Решение проблемы общих ГУ11 для уравнений теплопроводности и колебаний

37.Задачи на собственные значения для матричных операторов 38.Некоторые свойства матричной задачи на собственные значения 39.Сопряжённые и самосопряжённые ,эрмитово-сопряжённые и эрмитово-сопряжённые и эрмитово-дифференциальные операторы 40.Общий вид самосопряжённого дифференциального оперетора второго порядка с вещественными коэффициентами 41.Эрмитовость сопряжённых дифференциальных операторов и ГУ 42.Свойства собственных функций и собственных значений эрмитовых дифференциальных операторов 43.Приведение дифференциальных операторов к самосапряжённому виду 44.Метод вариации постоянных для эрмитово-дифференциального оператора 45.Функция Грина неоднородной краевой задачи для эрмитово-дифференциального оператора 46.Переход от экспонцениального ряда сФурье к интегральному ряду Фурье 47.Кратные преобразования Фурье 48.Преобразование Фурье и бета-функции 49.Решение однородной задачи Коши для УТ методом преобразования Фурье 50.Функция Грина для однородной задачи Коши для УТ 51.Примеры вычисления преобразований Фурье и свойства функции Грина 52.Решение задачи Коши для однородного уравнения колебаний методом преобразования Фурье 53.Вычисление функции Грина задачи Коши для УК 54.Неоднородная задача Коши для УТ

55. Неоднородная задача Коши для УК 56. Неоднородная задача Коши с ненулевыми НУ 57.Решение неоднородных обыкновенных ДУ методом преобразования Фурье 58.Функция Грина обыкновенных ДУ и их свойства в методе преобразования Фурье 59.Интегралы Фурье для функций Грина и лемма Жордана