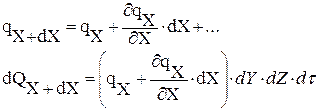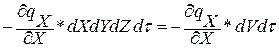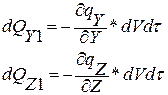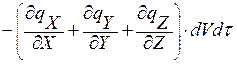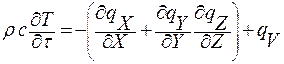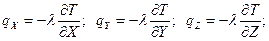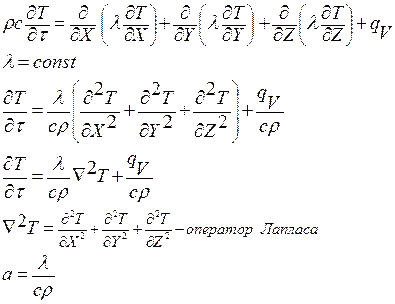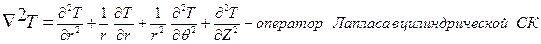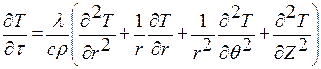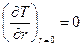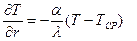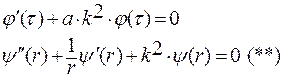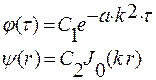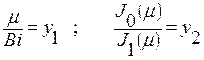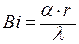Постановка задачи и вывод дифференциального уравнения теплопроводности для сплошного цилиндра. Аналитическое решение.
Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Из всего рассматриваемого объема выделим элементарный объем dV и процесс будем рассматривать в течении элементарного промежутка времени.
· Тепло физические параметры среды постоянны
· Температурной деформацией пренебрегаем
· Внутренний источник тепла , если он есть, распределен по всему объему
dQ1 – количество тепла подведенного к рассматриваемому объему dV за время dτ за счет процессов электропроводности
dQ2 – количество тепловой энергии, которой выделяется на dV за dτ за счет действия внутреннего источника тепла
dQ – изменение внутренней энергии рассматриваемого объема за dτ (изменение энтальпии тела).
Ø Методы переноса тепла: теплопроводность, тепловая конвекция, излучение
Ø Конвективный обмен – возможен только в подвижных средах. Перенос осуществляется только за счет перемещение самого вещества.
Ø Тепловое излучение – перенос тепла происходит в 2 этапа. Сначала тепло преобразуется в тепловую энергию, а затем обратно.
Ø Теплопроводность – перенос тепла в твердых телах, жидкостях или газах, если жидкость и газы неподвижны.
Механизм данного явления объясняется на основании молекулярно — кинетических изменений. Перенос энергии осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.
Теплопроводность в чистом виде существует только в твердых телах. А в подвижных средах теплообмен осуществляется за счет теплопроводности, конвекции и излучения.
По теплопроводности тепло распространяется от нагретых участков к холодным, то есть в сторону убывания температуры.
Температура определяет степень нагретости тела.
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела, поэтому необходимо дать определение температурному полю и градиенту температуры:
— температурным полем называется совокупность значений температуры в каждой точке пространства в данный момент времени
Геометрическое место точек в пространстве имеющих одинаковую температуру, называется изотермической поверхностью
Поскольку любая точка пространства в данный момент времени может иметь только одно значение температуры, то изотермические поверхности не пересекаются →
— температурный градиент – предел отношения изменения температуры ΔТ к расстоянию между изотермами по нормали Δn.
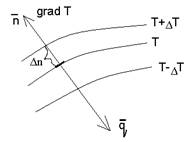
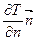
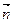
Является вектором, направленным по нормали к изотермической поверхности в сторону возрастания температуры его размерность [ 0 С/м]
Наибольшее изменение температуры может происходить по нормали к изотермическим поверхностям.
· Количества тепла, прошедшего через произвольную изотермическую поверхность за некоторый интервал времени τ – будем обозначать P [Вт]
· Количества тепла, прошедшего через произвольный изотермическую поверхность в единицу времени будем обозначать – тепловой поток Q [Дж].
· Тепловой поток отнесенный к единице поверхности, называется плотностью теплового потока – q [Вт/м 2 ]
· Закон Фурье (связь q и grad T). Фурье экспериментально установил что, количество переданного тепла пропорционально падению температуры, времени и площади сечения, перпендикулярного направлению распространению тепла
· λ – коэффициент теплопроводности – представляет собой количество тепла, которое роходит в единицу времени через один квадратный метр изотремической поверхности при температурном градиенте =1
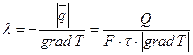
В общем случаи λ зависит от температуры
· С – теплоемкость – количество энергии необходимого для нагрева 1 кг вещества на 1 градус. [Дж/кг 0 С]
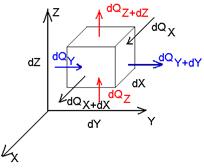
dQX1 = dQX — dQX+dX =
dQ1 = dQX1 + dQY1 + dQZ1 =
dQ2 = qV dV dτ, где qV – количества тепла выделившегося в единице объема в единицу времени (внутренний источник тепла).
dQ = dU = ρ C 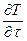
Из закона Фурье:
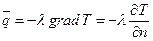
а – коэффициент температура проводность [м 2 / 0 С]
Постановка задачи:
1. рассматриваем сплошной цилиндр
2. процесс изотермический
3. цилиндрическая система координат
4. теплофизические свойства постоянны
5. внутреннего источника тепла нет (qV =0)
Переходим от декартовой системы координат к цилиндрической:
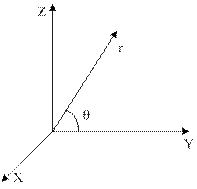 | Цилиндрические (Ц) и декартовые (Д) координаты связаны следующим образом: |
Д ® Ц 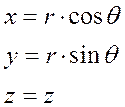 | Ц ® Д 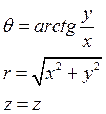 |
Оператор Лапласа для цилиндрической системы координат запишется:
С учетом поставленной задачи получаем:
Охлаждение (нагревание) бесконечного длинного цилиндра.
Цилиндр радиусом г0 отдает теплоту окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды Tcp постоянна. В начальный момент времени при τ = 0 температура является некоторой функцией T (r, 0) = f (r). 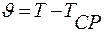
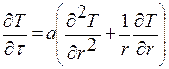
Граничные и начальные условия:
· при τ = 0 и 0 0 и r = 0
· при τ > 0 и r = r0
Сформулированную задачу решим с помощью разделения переменных, т. е.
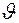
Подставив это выражение в уравнение (*),получим два обыкновенных дифференциальных уравнения вида
Если обозначить kr0 = μ , тогда частное решение уравнения (*) будет иметь вид:
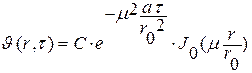
где 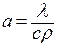
Постоянная μ определяется из граничных условий (r= r0), решение которых приводит к характеристическому уравнению:
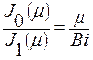
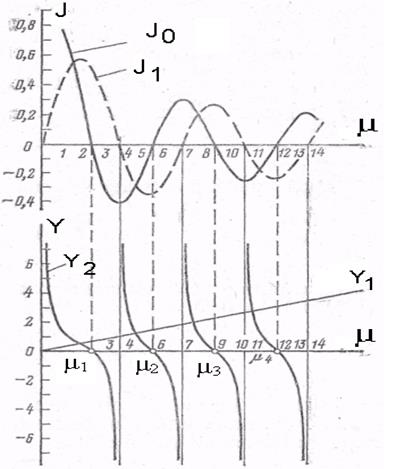
Уравнение (+) является трансцендентным, и его удобно решать графическим способом, обозначив:
· Отметим, что у2 обращается в нуль в тех точках, для которых Jo (μ) = 0.
· В тех точках, в которых функция J1 (μ1) обращается в нуль, функция у2 претерпевает разрыв непрерывности и становится равной ± оо.
Функции Jo (μ) и J1 (μ) являются периодическими затухающими функциями.
— Кривая у2 = напоминает котангенсоиду, но с убывающим периодом.
— Функция у1 графически представляет прямую линию, проходящую через начало координат.
Выполнив построение, как показано на рис, в точках пересечения функции у2 с прямой у1 получим значения корней характеристического уравнения
· Если рассматривать охлаждение цилиндра при условии Bi → 0
(практически Bi 2 = 2Bi.
· Если Fo ≥ 0,25, при вычислении безразмерной температуры 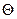
Дата добавления: 2016-04-19 ; просмотров: 2817 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Дифференциальное уравнение теплопроводности
В учебниках по теплопередаче, в том числе и в [1], приводится вывод дифференциального уравнения температурного поля движущейся жидкости, уравнение энергии
 | (1.12) |
где ср, Дж/(кг×К) – изобарная теплоемкость; r, кг/м 3 – плотность; l, Вт/(м×К) – коэффициент теплопроводности; wх, wy, wz – проекции вектора скорости движения жидкости; qv , Вт/м 3 – объемная плотность внутреннего тепловыделения жидкости.
Уравнение (1.12) записано для случая l=const.
Дифференциальное уравнение температурного поля для твердых тел называется дифференциальным уравнением теплопроводности и может быть получено из (1.12) при условии wх= wy= wz=0, ср= сv=с:

где 
Дифференциальное уравнение теплопроводности
 | (1.13) |
описывает нестационарное температурное поле твердых тел с внутренним тепловыделением (с внутренними источниками тепла). Такими источниками тепла могут быть: джоулева теплота, выделяемая при прохождении электрического тока по проводникам; теплота, выделяемая ТВЭЛами ядерных реакторов и т.д.
Дифференциальное уравнение теплопроводности (1.13), записанное в декартовых координатах, можно представить в цилиндрических (r, z, φ) и сферических (r, φ, ψ).
В частности, в цилиндрических координатах (r –радиус; φ – полярный угол; z — аппликата) дифференциальное уравнение теплопроводности имеет вид
 | (1.14) |
Условия однозначности
Дифференциальное уравнение описывает множество процессов теплопроводности. Чтобы выделить из этого множества конкретный процесс, необходимо сформулировать особенности этого процесса, которые называются условиями однозначности и включают в себя:
· геометрические условия, характеризующие форму и размеры тела;
· физические условия, характеризующие свойства участвующих в теплообмене тел;
· граничные условия, характеризующие условия протекания процесса на границе тела;
· начальные условия, характеризующие начальное состояние системы при нестационарных процессах.
При решении задач теплопроводности различают:
· граничные условия первого рода, когда задается распределение температуры на поверхности тела:
· граничные условия второго рода, когда задается плотность теплового потока на поверхности тела:
· граничные условия третьего рода, когда задается температура среды tж и коэффициент теплоотдачи между поверхностью и средой.
В соответствии с законом Ньютона-Рихмана тепловой поток, передаваемый с 1м 2 поверхности в среду с температурой tж,
В то же время этот тепловой поток подводится к 1м 2 поверхности из глубинных слоев тела теплопроводностью
Тогда уравнение теплового баланса для поверхности тела запишется в виде
 | (1.15) |
Уравнение (1.15) является математической формулировкой граничных условий третьего рода.
Система дифференциальных уравнений совместно с условиями однозначности представляет собой математическую формулировку задачи. Решения дифференциальных уравнений содержат константы интегрирования, которые определяются с помощью условий однозначности.
Контрольные вопросы и задания
1. Проанализируйте, какими способами передается теплота от горячей воды к воздуху через стенку батареи отопления: от воды к внутренней поверхности, через стенку, от наружной поверхности к воздуху.
2. Почему в правой части уравнения (1.3) стоит минус?
3. Проанализируйте с помощью справочной литературы зависимость λ(t) для металлов, сплавов, теплоизоляционных материалов, газов, жидкостей и ответьте на вопрос: как изменяется коэффициент теплопроводности с изменением температуры для этих материалов?
4. Как определяется тепловой поток (Q, Вт) при конвективной теплоотдаче, теплопроводности, тепловом излучении?
5. Запишите дифференциальное уравнение теплопроводности в декартовых координатах, описывающее трехмерное стационарное температурное поле без внутренних источников теплоты.
6. Запишите дифференциальное уравнение температурного поля проволоки, которая длительное время находится под напряжением при постоянной электрической нагрузке.
2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
2.1. Теплопроводность плоской стенки
при граничных условиях первого рода
Дано:плоская однородная стенка толщиной δ (рис. 2.1) с постоянным коэффициентом теплопроводности λ и постоянными температурами t1 и t2 на поверхностях.

Температурное поле стенки описывается дифференциальным уравнением теплопроводности (1.3) при следующих условиях:
· 
· 
· 
Температура стенки является функцией только одной координаты х и уравнение (1.13) принимает вид
 | (2.1) |
т.к. коэффициент температуропроводности стенки а ≠ 0.
Граничные условия первого рода:
| при х=0 t= t1 , | (2.2) |
| при х= δ t= t2. | (2.3) |
Выражения (2.1), (2.2), (2.3) являются математической постановкой задачи, решение которой позволит получить искомое уравнение температурного поля t= f (x).
Интегрирование уравнения (2.1) дает
При повторном интегрировании получим решение дифференциального уравнения в виде
| t=с1х+с2. | (2.4) |
Из уравнения (2.4) при условии (2.2) получим
а при условии (2.3)
Подстановка констант интегрирования с1 и с2 в уравнение (2.4) дает уравнение температурного поля
 | (2.5) |
по которому можно рассчитать температуру по толщине стенки на любой координате 0 2 ; t2, t3.
При стационарном режиме и постоянных температурах поверхностей стенки тепловой поток, передаваемый через трехслойную стенку, можно представить системой уравнений:
 | (2.8) |
 | (2.9) |
 | (2.10) |
 | (2.11) |
Сложив левые и правые части уравнений (2.11), получим расчетную формулу для плотности теплового потока, передаваемого через трехслойную стенку
 | (2.12) |
Температуры на границах слоев t2 и t3 можно рассчитать по уравнениям (2.8) – (2.10) после того, как найдена плотность теплового потока (q) по (2.12).
Общий вид уравнения (2.12) для многослойной плоской стенки, состоящей из п однородных слоев с постоянными температурами на наружных поверхностях 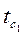

 | (2.13) |
Средний коэффициент теплопроводности многослойной стенки называют эффективным (λэф). Он равен коэффициенту теплопроводности однородной стенки, толщина и термическое сопротивление которой равны толщине и термическому сопротивлению многослойной стенки
 | (2.14) |
2.2. Теплопроводность цилиндрической стенки
при граничных условиях первого рода


(рис. 2.3).
Определить: уравнение температурного поля
t = f (r), тепловой поток, передаваемый через стенку
Q, Вт.
Дифференциальное уравнение теплопроводности в цилиндрических координатах (1.14) для условий данной задачи:


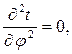
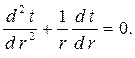 | (2.15) |
Граничные условия первого рода:
| при r=r1 t=t1 , | (2.16) |
| при r=r2 t=t2 . | (2.17) |
Порядок решения системы уравнений (2.15) – (2.17) тот же, что и в случае плоской стенки: находится общий интеграл дифференциального уравнения второго порядка (2.15), который содержит две константы интегрирования
с1 и с2 . Последние определяются с помощью граничных условий (2.16) и (2.17) и после подстановки их значений в решение дифференциального уравнения (общий интеграл) получаем уравнение температурного поля цилиндрической стенки t = f (r) в виде
 | (2.18) |
где r1 

Нетрудно убедиться, что при подстановке в (2.18) r= r1 получим t=t1 , при r=r2 получим t=t2. Распределение температуры по толщине цилиндрической стенки, в соответствии с (2.18) подчиняется логарифмическому закону (рис. 2.3).
Для определения теплового потока воспользуемся законом Фурье:
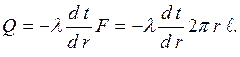 | (2.19) |
Если взять производную 
 | (2.20) |
В технических расчетах часто тепловой поток вычисляется для 1 м длины трубы:
и называется линейной плотностью теплового потока.
Запишем уравнение (2.20) в виде
где 
Для трехслойной цилиндрической стенки (трубы, покрытой двумя слоями тепловой изоляции) с известными постоянными температурами поверхностей (t1 и t4), с известными геометрическими размерами (r1 , r2, r3, r4 , 
 | (2.21) |
Совместное решение системы уравнений (2.21) дает расчетную формулу для теплового потока, передаваемого через трехслойную стенку при заданных температурах на поверхностях,
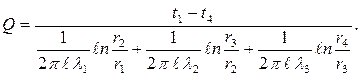 | (2.22) |
Температуры на границах слоев (t2, t3) можно рассчитать по уравнениям (2.21).
Для многослойной цилиндрической стенки, состоящей из п слоев, формулу (2.22) можно записать в общем виде
 | (2.23) |
Эффективный коэффициент теплопроводности для многослойной цилиндрической стенки, как и для многослойной плоской стенки, определяется из равенства суммы термических сопротивлений многослойной стенки термическому сопротивлению однородной стенки той же толщины, что и многослойная. Так, для двухслойной тепловой изоляции трубы
(рис. 2.4) эффективный коэффициент теплопроводности (λэф) определ ится из равенства
2.3. Теплопроводность плоской и цилиндрической стенок
при граничных условиях третьего рода (теплопередача)
Граничные условия третьего рода состоят в задании температуры жидкости (tж) и коэффициента теплоотдачи ( 
Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей.
Примерами теплопередачи служит перенос теплоты от дымовых газов к воде через стенку трубы парового котла, перенос тепла от горячей воды к окружающему воздуху через стенку батареи отопления и т.д.
Теплообмен между поверхностью и средой (теплоносителем) может быть конвективным, если теплоноситель – жидкость (вода, нефть и т.д.) или радиационно-конвективным, когда теплота передается путем конвективного теплообмена и излучением, если теплоноситель – газ (дымовые газы, воздух и т.д.).
Рассмотрим теплопередачу через плоскую и цилиндрическую стенки при условии только конвективного теплообмена на поверхностях. Теплопередача с радиационно-конвективным теплообменом (сложным теплообменом) на поверхностях будет рассмотрена позже.
Плоская стенка(рис. 2.5)

Плотность теплового потока q описывается следующими уравнениями в зависимости от способа передачи теплоты:
– от горячей жидкости к стенке
 | (2.24) |
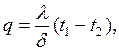 | (2.25) |
– от стенки к холодной жидкости
 | (2.26) |
Записав уравнения (2.24) – (2.26) в виде
 | (2.27) |
и сложив почленно правые и левые части уравнений (2.27), получим формулу для расчета теплопередачи (q, Вт/м 2 ) через плоскую стенку в виде
 | (2.28) |
Величины 
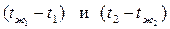
Температуры на поверхностях стенки t1 и t2 можно рассчитать по уравнениям (2.24) – (2.26) после того, как определена плотность теплового потока (q) по уравнению (2.28).
Формулу (2.28) можно записать в виде
 | (2.29) |
где 
Теплопередача через многослойную плоскую стенку рассчитывается по формуле
 | (2.30) |
Цилиндрическая стенка(рис. 2.6)

Для цилиндрической стенки, по аналогии с плоской стенкой, можно записать следующую систему уравнений:
 | (2.31) |
 | (2.32) |
 | (2.33) |
где 
Записав уравнения (2.31) – (2.33) относительно разностей температур, а затем сложив правые и левые части уравнений, получим формулу для расчета теплопередачи (Q, Вт) через цилиндрическую стенку в виде
 | (2.34) |
Температуры на поверхностях стенки t1 и t2 рассчитываются по уравнениям (2.31) – (2.33).
Формулу (2.34) также можно представить в виде
где  – коэффициент теплопередачи цилиндрической стенки. – коэффициент теплопередачи цилиндрической стенки. |
Для металлических труб с 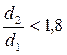


Вопрос 26 дифференциальное уравнение теплопроводности для нестационарного температурного поля в цилиндрических координатах ?
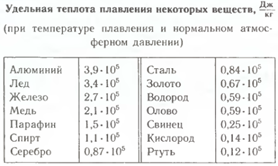
Вопрос 23 чему равна удельная теплота плавления льда
Удельная теплота плавления находится по формуле:
λ=Q/m,
где Q – это количество теплоты, необходимое для того, чтобы расплавить тело массой m.
при отвердевании вещества выделяют такое же количество тепла, которое требовалось затратить на их расплавление. Молекулы, теряя энергию, образуют кристаллы, будучи не в силах сопротивляться притяжению других молекул. И опять-таки, температура тела не будет понижаться вплоть до того момента, пока не отвердеет все тело, и пока не выделится вся энергия, которая была затрачена на его плавление. То есть удельная теплота плавления показывает, как сколько надо затратить энергии, чтобы расплавить тело массой m, так и сколько энергии выделится при отвердевании данного тела.
Для примера, удельная теплота плавления воды в твердом состоянии, то есть, Удельная теплота плавления льда равна 3,4*10^5 Дж/кг
Удельная теплота плавления льда равна 3,4 умножить на 10 в 5 степени джоуль/кг
Обозначают удельную теплоту плавления греческой буквой λ (лямбда), а единицей измерения является 1 Дж/кг
Вопрос 24 Обозначим L1 – удельную теплоту парообразования, L2 – удельную теплоту плавления. Что больше?
Поскольку при парообразовании тело получает энергию, можно сделать вывод, что внутренняя энергия тела в газообразном состоянии больше, чем внутренняя энергия тела той же массы в жидком состоянии. Поэтому, при конденсации пар отдаёт то количество энергии, которое потребовалось для его образования
Удельная теплота парообразования – физическая величина, показывающая количество теплоты, требуемое для превращения в пар 1 кг вещества без изменения его температуры. Коэффициенты «r» для различных веществ, как правило, различны. Они измерены опытным путём и занесены в специальные таблицы
Удельная теплота плавления – физическая величина, показывающая количество теплоты, требуемое для превращения в жидкость 1 кг вещества без изменения его температуры. Коэффициенты «λ» для различных веществ, как правило, различны. Они измерены опытным путём и занесены в специальные таблицы
| Удельные теплоты плавления и парообразования, кДж/кг | |
| Лёд | Вода |
| Железо | Спирт |
| Свинец | Свинец |
Удельная теплота парообразования больше
Вопрос 25 дифференциальное уравнение теплопроводности для двумерного нестационарного температурного поля в декартовых координатах ?
хi= x, y, z – декартовая система координат;
Если вдоль одной из координат температура остается постоянной, то математически это условие записывается (например, для координаты z) следующим образом: дТ/дz=0.
В этом случае поле называется двумерным и записывается:
для нестационарного режима Т=Т(х, у, t);
для стационарного режима Т=Т(х, у).
Уравнения двухмерного температурного поля для режима
Вопрос 26 дифференциальное уравнение теплопроводности для нестационарного температурного поля в цилиндрических координатах ?
хi= r, φ, z – цилиндрическая система координат;
Температурное поле есть совокупность значений температуры во всех точках данной расчетной области и во времени.
Температурное поле измеряют в градусах Цельсия и Кельвинах и обозначают также как и в ТТД : 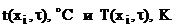
В тепловых расчетах используют следующие системы координат:
хi= r, φ, z – цилиндрическая система координат;
Температурное поле, которое изменяетсяво времени, называют нестационарным температурным полем. И наоборот, температурное поле, которое не изменяетсяво времени, называют стационарным температурным полем.
цилиндрических координатах (г – радиус; φ – полярный угол; z – аппликата) дифференциальное уравнение теплопроводности имеет вид

http://megaobuchalka.ru/8/46137.html
http://poisk-ru.ru/s227t10.html