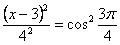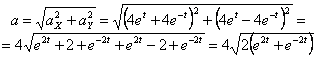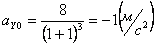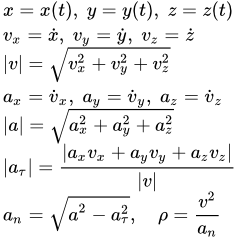Вывод уравнения траектории по уравнениям движения

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

3.1. На проволочной окружности радиусом r надето колечко М, через него проходит стержень ОА, который поворачивается вокруг точки О с постоянной угловой скоростью.

Определить уравнения движения и уравнение траектории колечка М, если бы в начальный момент стержень ОА был вертикален.

Дано: , .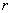

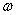
Найти: , , .

Решение: Из рисунка видно, что амплитуда по оси равна радиусу окружности. При повороте стержня на угол , кольцо М проходит по окружности угол , из чего можно сделать вывод, что угловая скорость кольца М по окружности в два раза больше угловой скорости стержня . Координата в начальный момент равна нулю, так как стержень находится в вертикальном положении, поэтому координата изменяется по синусу и его уравнение:

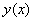
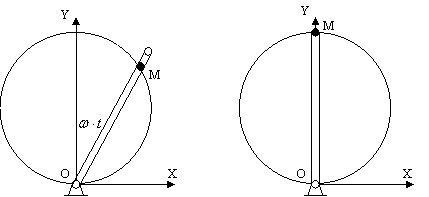
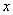
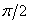
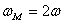
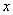
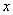
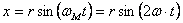
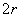
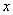
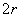
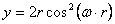
Относительно точки О координата может изменяться от нуля до , поэтому амплитуда по оси равна . В начальный момент координата занимает максимальное значение, поэтому координата изменяется по косинусу и так как ее значение не может быть отрицательно, то, очевидно по квадрату косинуса:

Уравнение траектории – круг с центром в точке (0; r ) будет:

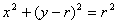
Второй рисунок – начальное положение.

4. 1 . Даны уравнения движения точки.

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при 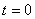и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .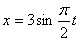

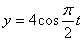
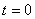
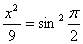
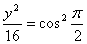
Решение: 1. Из первого уравнения и из второго .

Уравнение траектории получается суммированием полученных уравнений:

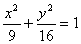
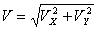
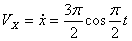
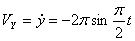
2. Модуль скорости точки определяется по формуле , где

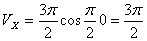
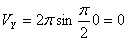
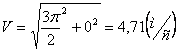
При t =0: , и тогда ,

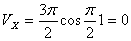
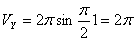
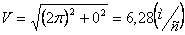
При t =1 c : и и тогда .

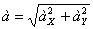
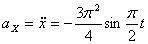
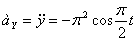
Модуль ускорения точки определяется по формуле , где

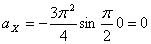
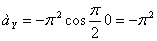
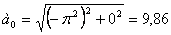
При t =0: , и тогда ,

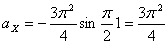
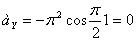
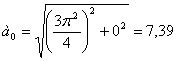
При t =1 c : , и тогда .

3. Траектория представляет собою эллипс с центром в начале координат (0;0) и полуосями 3и 4.

4. 2 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .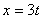

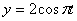
Найти: , , , , .

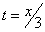
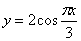
Решение Чтобы найти уравнение траектории точки выведем из уравнения время , подставляя во второе уравнение, получим уравнение траектории:

Скорость точки по осям:

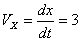
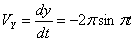
Общая скорость точки:

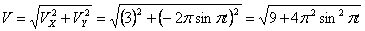
Скорости в заданные моменты времени:

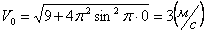
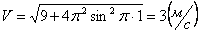
Ускорения точки по осям:

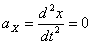
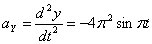
Общее ускорение точки:

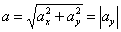
Ускорения в заданные моменты времени:

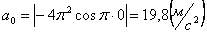
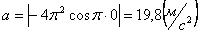
4. 3 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .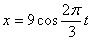

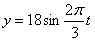
Найти: , , , , .

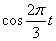
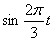
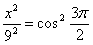
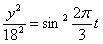
Решение Чтобы найти уравнение траектории точки необходимо из уравнений движения исключить время. Для этого уравнения движения разрешим относительно и и возведем полученные результаты в квадрат:

Тогда уравнение траектории 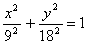— эллипс с полуосями 9 и 18, центр которого в точке (0;0).

Скорость точки по осям:

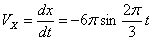
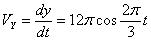
Общая скорость точки:

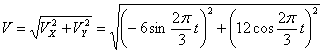
Скорости в заданные моменты времени:

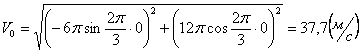
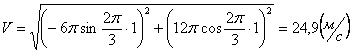
Ускорения точки по осям:

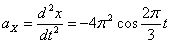
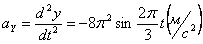
Общее ускорение точки:

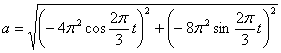
Ускорения в заданные моменты времени:

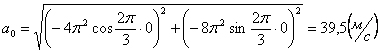
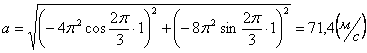
4. 4 . Даны уравнения движения точки.

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при 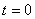и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .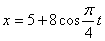

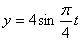
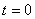
Найти: , , ,

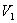
Решение: 1. Из уравнений и выражаем:

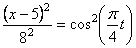
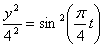
Складывая их получим уравнение траектории точки:

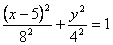
Траектория является эллипсом с полуосями 8 и 4см с центром в точке (5;0).

2. Скорости точки по осям:

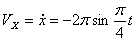
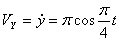
Модуль скорости точки определяется по формуле:

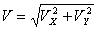
Для момента времени t =0:

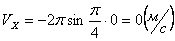
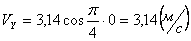
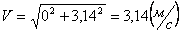
Для момента времени t =1 c :

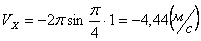
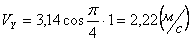
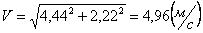
Ускорения по осям:

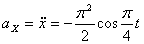
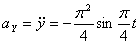
Модуль ускорения точки определяется по формуле:

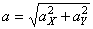
Для момента времени t =0:

, и

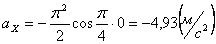
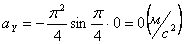
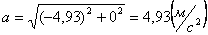
Для момента времени t =1:

, и

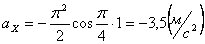
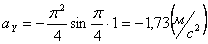
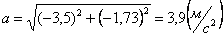
4. 5 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .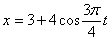

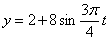
Найти: , , , , .

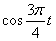
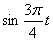
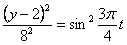
Тогда уравнение траектории 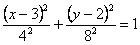— эллипс с полуосями 4 и 8, центр которого в точке (3;2).

Скорость точки по осям:

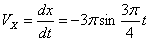
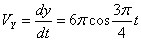
Общая скорость точки:

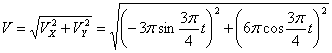
Скорости в заданные моменты времени:

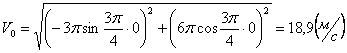
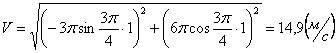
Ускорения точки по осям:

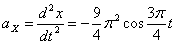
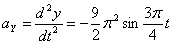
Общее ускорение точки:

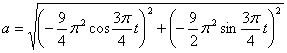
Ускорения в заданные моменты времени:

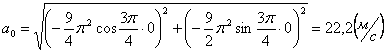
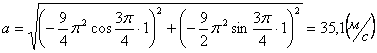
4. 6 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .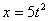

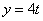
Найти: , , , , .

Решение: Из уравнения выразим время:

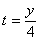
Подставив время в уравнение , получим уравнение траектории :

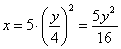
Скорость точки по осям:

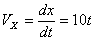
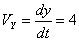
Общая скорость точки:

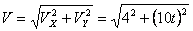
Скорости в заданные моменты времени:

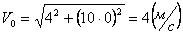
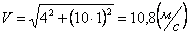
Ускорения точки по осям:

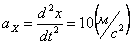
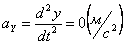
Общее ускорение точки: .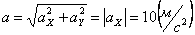

4. 7 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .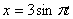

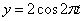
Найти: , , , , .

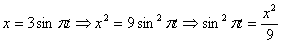
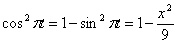
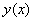
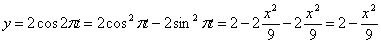
Решение: Из уравнения выразим: , тогда . Из уравнения выражаем уравнение траектории : .

Скорость точки по осям:

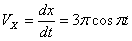
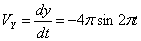
Общая скорость точки:

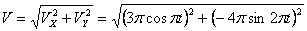
Скорости в заданные моменты времени:

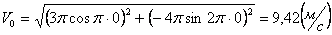
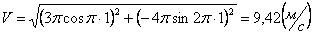
Ускорения точки по осям:

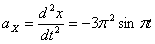
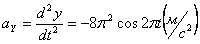
Общее ускорение точки:

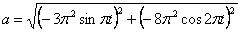
Ускорения в заданные моменты времени:

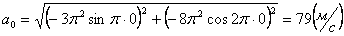
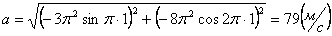
4. 8 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .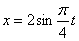

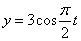
Найти: , , , , .

Решение: Из уравнения выразим:

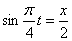
Распишем уравнение :

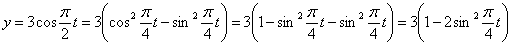
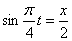
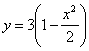
Подставив в уравнение , получим уравнение траектории:

Скорость точки по осям:

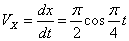
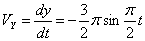
Общая скорость точки:

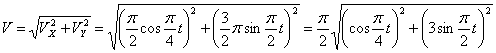
Скорости в заданные моменты времени:

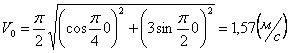
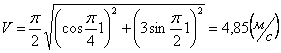
Ускорения точки по осям:

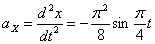
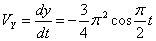
Общая скорость точки:

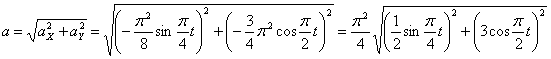
Скорости в заданные моменты времени:

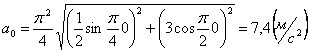
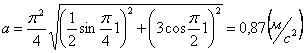
4. 9 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .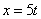

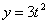
Найти: , , , , .

Решение: Из уравнения выразим время:

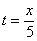
Подставив время в уравнение , получим уравнение траектории :

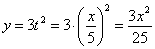
Скорость точки по осям:

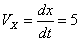
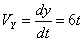
Общая скорость точки:

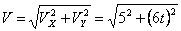
Скорости в заданные моменты времени:

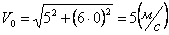
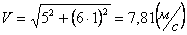
Ускорения точки по осям:

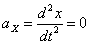
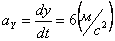
Общее ускорение точки:

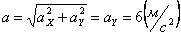
4.1 0 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .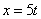

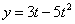
Найти: , , , , .

Решение: Из уравнения выразим время:

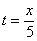
Подставив время в уравнение , получим уравнение траектории :

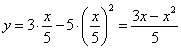
Скорость точки по осям:

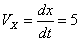
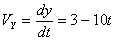
Общая скорость точки:

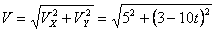
Скорости в заданные моменты времени:

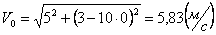
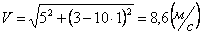
Ускорения точки по осям:

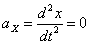
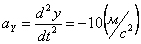
Общее ускорение точки:

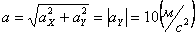
4.1 1 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .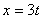

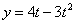
Найти: , , , , .

Решение: Из уравнения выразим время:

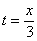
Подставив время в уравнение , получим уравнение траектории :

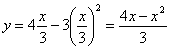
Скорость точки по осям:

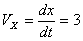
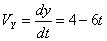
Общая скорость точки:

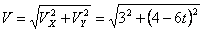
Скорости в заданные моменты времени:

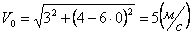
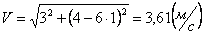
Ускорения точки по осям:

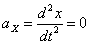
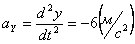
Общее ускорение точки:

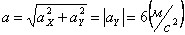
4.1 2 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .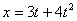

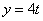
Найти: , , , , .

Решение: Из уравнения выразим время:

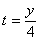
Подставив время в уравнение , получим уравнение траектории :

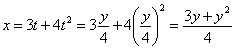
Скорость точки по осям:

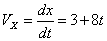
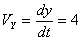
Общая скорость точки:

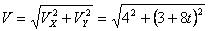
Скорости в заданные моменты времени:

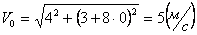
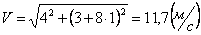
Ускорения точки по осям:

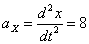
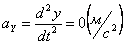
Общее ускорение точки:

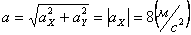
4. 13 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .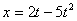

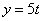
Найти: , , , , .

Решение: Из уравнения выразим время:

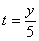
Подставив время в уравнение , получим уравнение траектории :

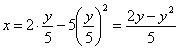
Скорость точки по осям:

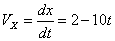
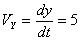
Общая скорость точки:

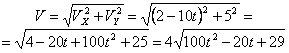
Скорости в заданные моменты времени:

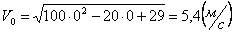
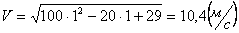
Ускорения точки по осям:

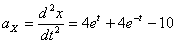
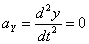
Общее ускорение точки:

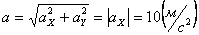
4. 14 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .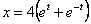

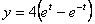
Найти: , , , , .

Решение: Возведем оба уравнения в квадрат и вычтем:

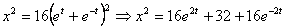
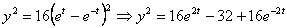
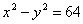
Это уравнение окружности радиусом 8см.

Скорость точки по осям:

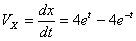
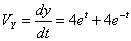
Общая скорость точки:

Скорости в заданные моменты времени:

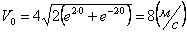
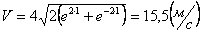
Ускорения точки по осям:

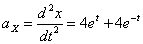
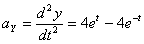
Общее ускорение точки:

Ускорения в заданные моменты времени:

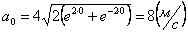
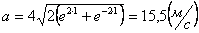
4. 15 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .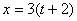

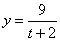
Найти: , , , , .

Решение: Из уравнения выразим:

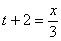
Подставив время в уравнение , получим уравнение траектории :

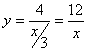
Скорость точки по осям:

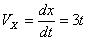
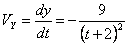
Общая скорость точки:

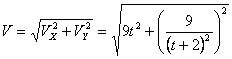
Скорости в заданные моменты времени:

Ускорения точки по осям:

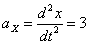
Общее ускорение точки:

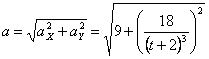
Ускорения в заданные моменты времени:

4. 16 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .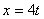

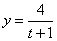
Найти: , , , , .

Решение: Из уравнения выразим время:

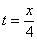
Подставив время в уравнение , получим уравнение траектории :

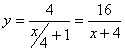
Скорость точки по осям:

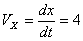
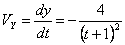
Общая скорость точки:

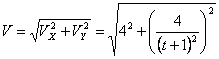
Скорости в заданные моменты времени:

Ускорения точки по осям:

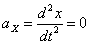
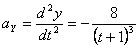
Ускорения в заданные моменты времени:

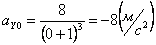
Общее ускорение точки:

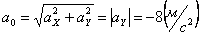
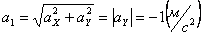
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

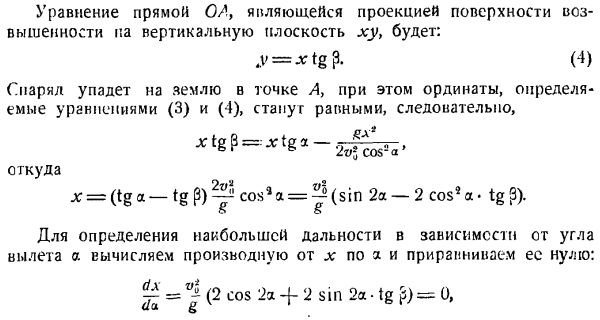
Траектория и уравнения движения точки

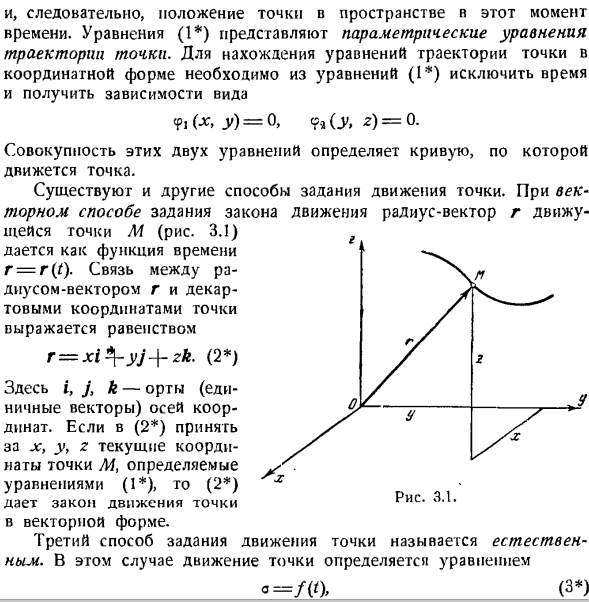
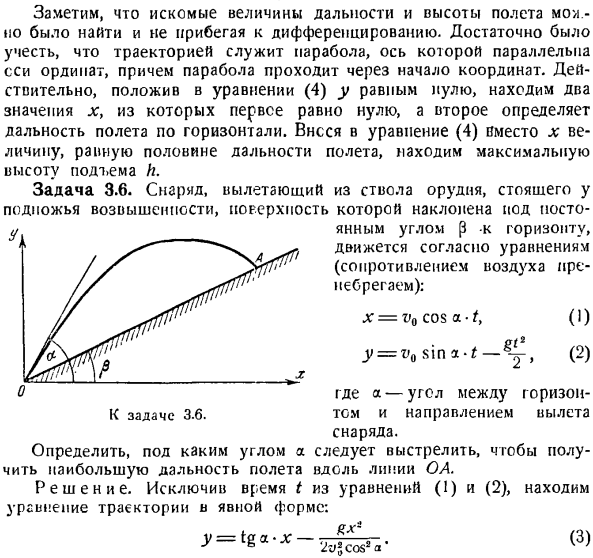
Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.

Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *( Людмила Фирмаль

Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS Людмила Фирмаль

Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря

Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1） г = Б, потому что КТ(2） Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3） решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4） Sin2 е

Или в конце： — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:

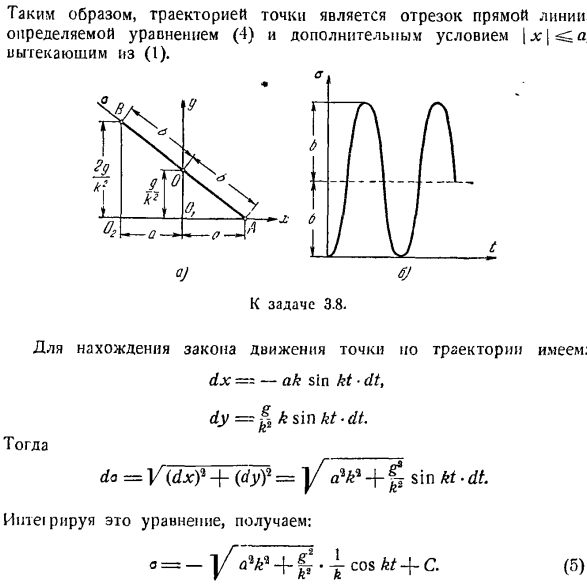
Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис. в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).

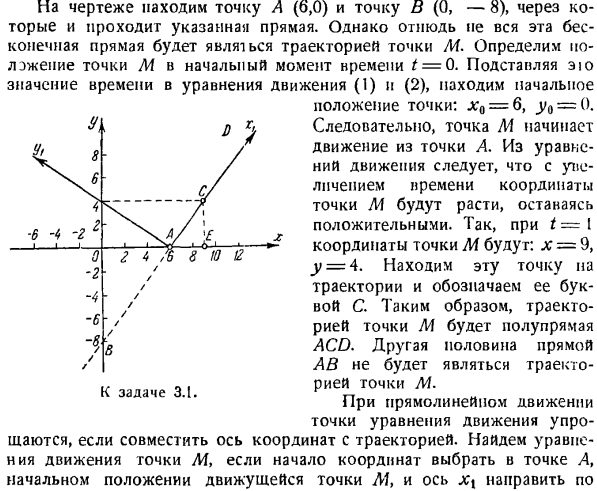
log A x cos2 a следовательно 2 значения x\ Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.

Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * \ — ый + ЗК. (2 ） Где i, j и k-единичные векторы (единичные векторы) осей. (2)

Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /( (). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ？ =?(’) * (5 *）

Уравнение движения для цилиндрических координат： р = п(о> т = м р = РЗ). (си *） м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

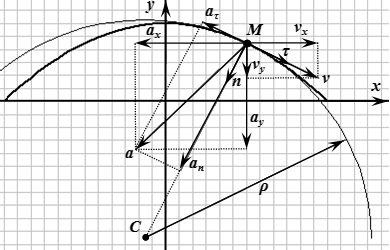
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
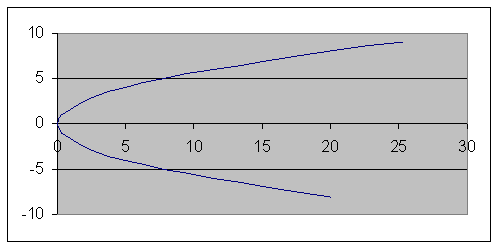
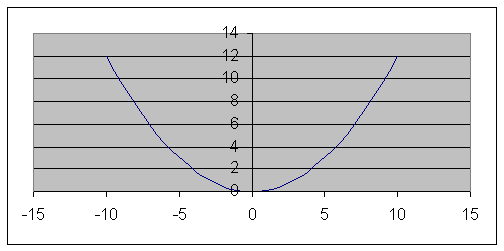
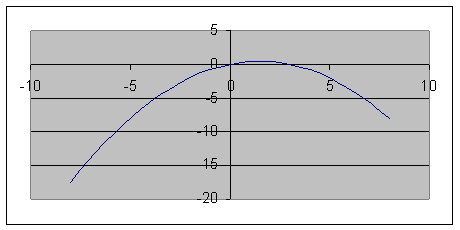
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

источники:

http://lfirmal.com/traektoriya-i-uravneniya-dvizheniya-tochki/

http://1cov-edu.ru/mehanika/kinematika/tochki/koordinatnyj-sposob-zadaniya-dvizheniya/