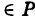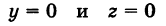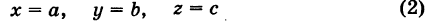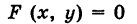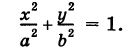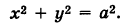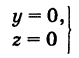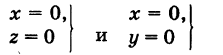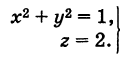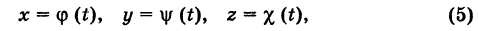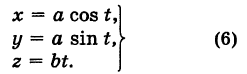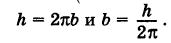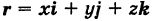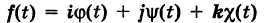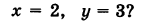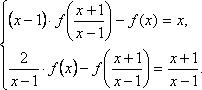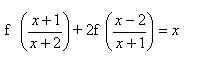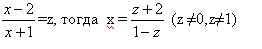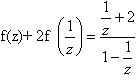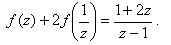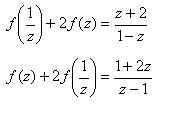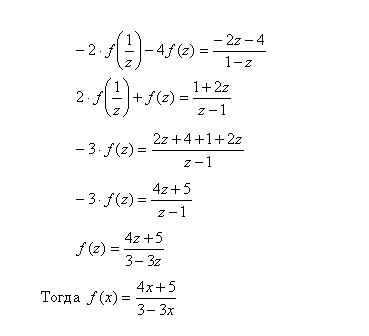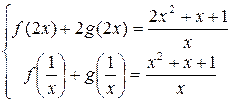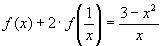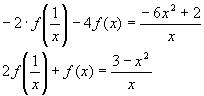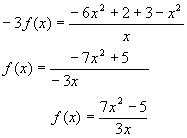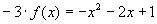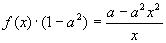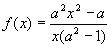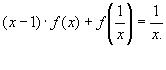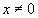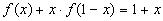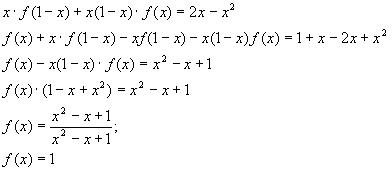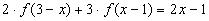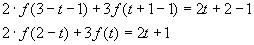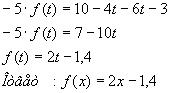X и z удовлетворяют уравнению

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Уравнения поверхности и линии в пространстве

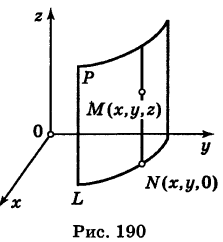
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

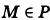
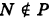
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

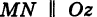
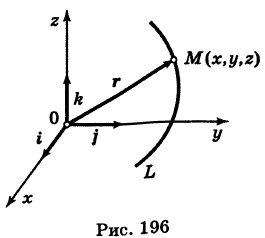
Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой (образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

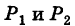
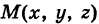
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 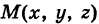, координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

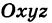
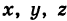
Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

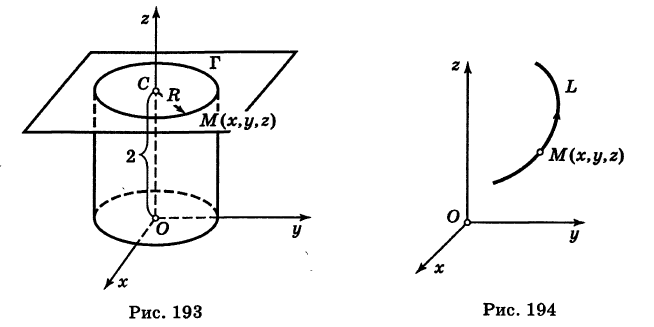
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 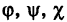— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

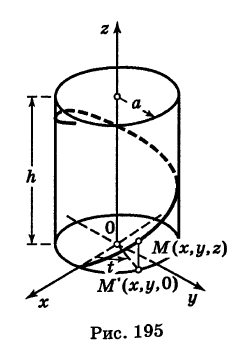
Написать уравнения винтовой линии радиуса а и шага 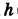(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 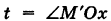и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

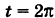
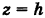
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

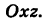
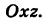
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

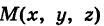
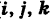
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

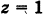
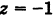
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Решение функциональных уравнений методом подстановки

Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.

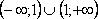
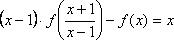
1. Найдите все функции, определённые на множестве , удовлетворяющие соотношению .

Решение:

Придадим x значение . Получим

.

Отсюда .

Получим систему

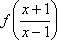
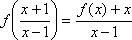
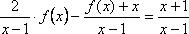
Из уравнения (1) выразим и подставим в уравнение (2).

; ;

Отсюда ;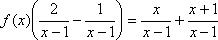

;

.

Проверим, действительно ли функция f(x) удовлетворяет уравнению .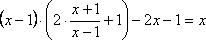

Ответ: .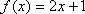

2. Найти функцию, удовлетворяющую уравнению

Решение:

2) Подставим в исходное уравнение, получим

3)Заменим z на 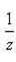получим

или после преобразований в правой части уравнения:

4)Итак, получили два уравнения:

5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:

3.Пусть 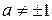— некоторое действительное число. Найти функцию f(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению

,где g – заданная функция, определённая при x ≠ 1.

Решение:При замене

получаем систему

.

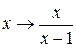
решением которой при a 2 ≠ 1 является функция

Ответ:

4.Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):

Решение:

В первом уравнении сделаем подстановку 2x = 1/z.

и первое уравнение принимает вид:

или

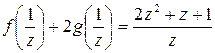
В результате получаем систему уравнений:

решение которой g(x) = 1/x, f(x) = x+1.

Ответ:g(x) = 1/x, f(x) = x+1.

5.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у. (1)

Решение:

Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.

Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у ? R.

6.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у. (2)

Решение:

Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.

7.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению

f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)

Решение:

Поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (3) получаем f(х)= х 2 -х+1 .

Ответ: f(х)= х 2 -х+1.

8.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению

f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (4)

Решение:

Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х 2 +6х+6)у=0 относительно х получаем х₁= -1, х₂= -5. Подстановка любого из этих значений в (4) дает нам f(у)=у 2 -4у.

9.Решите следующие функциональные уравнения.

в) f(x+y)+f(x-y)=2f(x)cos y

Решение:

а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.

б) Положим y=x-1/x , затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим

в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= — f(x). Заменив у на у+π/2, получаем

заменив теперь х- π/2 на х, имеем:

и с учетом предыдущего:

Положив х=0, получаем отсюда и из исходного уравнения:

Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.

10.

Решение: 1) Заменим на , получим или .

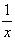
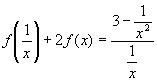
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

11. 2

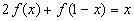
Решение: 1)Заменим в уравнении на , получим 2 .

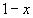
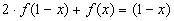
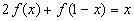
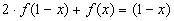
2) Умножим обе части исходного уравнения 2 на (-2) и сложим с уравнением 2 ,

получим:

12.

Решение:

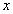
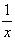
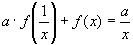
1) Заменим в уравнение на , .

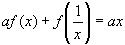
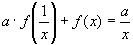
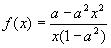
2)Умножим уравнение на и вычтем из уравнения , получим —

, где а

13.

Решение:

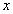
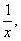
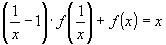
1)Заменим в уравнении на получим .

2)Выразим из исходного уравнения 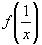, получим

или .

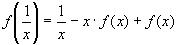
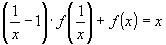
3)Подставим в уравнение , получим .

14.

Решение:

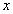
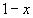
1.Заменим на , получим

2.Умножим обе части уравнения на и вычтем из уравнения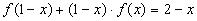

15.

Решение:1)Пусть 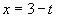, тогда уравнение принимает вид:

2)Пусть 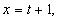тогда исходное уравнение принимает вид:

3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:

16.

Решение:

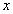
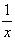
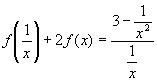
1) Заменим на , получим или .

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Глава 2. Функции комплексного переменного

Множества точек на плоскости

Рассмотрим некоторые вспомогательные геометрические понятия.

$|z|$ — расстояние от точки $z$ до начала координат;

$|z-z_0|$ — расстояние между точками $z$ и $z_0$;

$\$ — окружность с центром в точке $z_0$ и радиусом $R$;

$\^<\delta>(z_0)=\emptyset$, где $K_<0>^<\delta>(z_0): 0 1$ (внешность окружности) представляют собой односвязные области, так как имеют по одной границе.

2. Круговое концентрическое кольцо $D: r 0$, не является областью. Множество содержит точки, заполняющие I и III четверти. Множество является открытом, но нарушено свойство связности, так как точки из I и III четвертей нельзя соединить непрерывной линией, целиком состоящей из точек множества.

5. Кольцо $1 1$), то степень $\alpha^\beta$ имеет ровно $q$ различных значений. Во всех других случаях степень имеет бесконечное множество значений.

Обратные тригонометрические функции

Обратные тригонометрические функции также являются многозначными функциями. $$ \begin \mboxz=-\mathbf i \mbox(z+\sqrt), &\mboxz= -\mathbf i \mbox(\mathbf i z+\sqrt<1-z^2>), \\ \mboxz=-\frac<\mathbf i> <2>\mbox\displaystyle\frac<1+\mathbf i z><1-\mathbf i z>,&\mboxz=-\frac<\mathbf i> <2>\mbox\displaystyle\frac.\\ \end $$ При вычислении арккосинуса и арксинуса приходится извлекать квадратный корень из комплексного числа, то есть записывать два значения, для каждого из которых вычисляется логарифм. Для главного значения обратной тригонометрической функции выбирается то значение квадратного корня из комплексного числа, главное значение аргумента которого $\mbox\xi\in[0,\pi]$. Тогда все остальные значения будут получатся из главного по формуле: $$ \begin \mboxz=\pm\mboxz+2\pi k, k\in Z & \\ \mboxz= \pm\mboxz+2\pi k, k\in Z &.\\ \end $$

Предел и непрерывность функции

В дальнейшем мы будем рассматривать (если не будет специальной оговорки) однозначные функции. Если $w=g(z)$ — многозначная функция, то мы берем однозначную ветвь этой многозначной функции. Например, для $w=\mbox\,z=\mbox\,|z| + \mathbf i \mbox\,z+\mathbf i 2\pi k$ выбираем однозначные ветви: $$ w_0=\mbox\,|z| + \mathbf i \mbox\,z, \,\, w_1=\mbox\,|z| + \mathbf i \mbox\,z ++\mathbf i 2\pi, \dots $$

Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции вещественного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.

Пусть функция $w=f(z)$ определена и однозначна в некоторой окрестности $z_0$, исключая, может быть, саму точку $z_0$.

Конечная точка $A=a+\mathbf i b$ называется пределом функции $w=f(z)=u(x,y)+\mathbf i v(x,y)$ при $z\to z_0=x_0+\mathbf i y_0$, если действительные функции $u(x,y)$, $v(x,y)$ двух переменных $x$, $y$ стремятся соответственно к пределам $a$ и $b$ при $x\to x_0$, $y\to y_0$ $$ \lim\limits_<(x,y)\to(x_0,y_0)>u(x,y) = a, \quad \lim\limits_<(x,y)\to(x_0,y_0)>v(x,y) = b. $$ В этом случае пишут $\lim\limits_f(z)=A=a+\mathbf i b$.

Предел функции не должен зависеть от способа стремления $z$ к $z_0$.

Для комплексных функций имеют место свойства, аналогичные соответствующим свойствам для пределов вещественных функций. Если для двух функций $w_1(z)$ и $w_2(z)$ существуют пределы $B_1=\lim\limits_w_1(z)\neq\infty$, $B_2=\lim\limits_w_2(z)\neq0, \neq\infty$, то существуют пределы: \begin \begin &\lim\limits_(w_1(z)\pm w_2(z))=B_1\pm B_2,\\ &\lim\limits_(w_1(z)\cdot w_2(z))=B_1\cdot B_2,\\ &\lim\limits_\frac=\frac.\\ \end \end

Определение предела можно сформулировать также с помощью понятия окрестности (по Коши):

Если функция $w=f(z)$ определена в некоторой окрестности точки $z_0$ (но не обязательно в самой точке $z_0$) и если для любого $\varepsilon>0$ можно указать такое $\delta(\varepsilon)>0$, что как только точка $z$ попадет в $\delta$–окрестность точки $z_0$: $|z-z_0| 1) , определяем, что $u_x =3x^2-3y^2$, $v_x =6xy$, и, следовательно, сама $$ f'(z)=3x^2-3y^2+6\mathbf i xy=3(x^2+2\mathbf i xy-y^2)=3(x+\mathbf i y)^2=3z^2. $$

О т в е т: $f'(z)=3z^2.$

Аналитические функции

Функция $f(z)$ называется аналитической (или голоморфной, или регулярной) в конечной точке $z_0$, если она дифференцируема в каждой точке некоторой окрестности точки

Функция $f(z)$ однозначная и дифференцируемая в каждой точке области $D$ называется аналитической (иначе регулярной или голоморфной) в этой области.

Точки плоскости $z$, в которых однозначная функция $f(z)$ аналитична, называются правильными точками $f(z)$. Точки, в которых функция $f(z)$ не является аналитической, называются особыми точками этой функции.

Из определений видно, что понятие аналитичности и дифференцируемости в области совпадают,
в то время как условие аналитичности в точке является более жестким, чем условие дифференцируемости в точке.

Пример 1. Аналитической функцией является полином $$ P_n(z)=a_0z^n+a_1z^+\ldots+a_z+a_n,\quad a_0,a_1,\dots,a_n \in \mathbb C_<>, $$ так как он имеет производные во всех точках комплексной плоскости $z$.

Пример 2. Рациональная функция $$ R(z)=\frac, \quad P(z) \mbox < и >Q(z) \mbox< - полиномы>,$$ имеет производную в каждой точке, где $Q(z)\ne 0$. Поэтому $R(z)$ аналитична в области, полученной из плоскости $z$ удалением (выкалыванием) конечного числа точек, в которых $Q(z)=0$.

Пример 3. Функция $f(z)=z\cdot\bar$ не является аналитической ни в одной точке комплексной области. Условия Коши-Римана выполняются только в точке $z=0$, следовательно функция является дифференцируемой только в одной точке и не дифференцируема в окрестности этой точки.

Функция аналитическая во всей комплексной плоскости $ \mathbb C_<> $ называется целой функцией. Например, целыми являются функции $w=e^z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=z^n$, $w=P_n(z)$.

Связь аналитических функций с гармоническими

Пусть дана функция $f(z)=u(x,y) + \mathbf i v(x,y)$, аналитическая в некоторой области $D$. Тогда во всех точках области $D$ функции $u(x,y)$ и $v(x,y)$ удовлетворяют условиям Коши-Римана.

Выясним, любая ли функция двух переменных $x$ и $y$ может служить вещественной или мнимой частями некоторой аналитической функции.

Дифференцируя снова первое из условий по $y$, а второе по

Видим, что функции $u(x,y)$ и $v(x,y)$ должны удовлетворять одному и тому же дифференциальному уравнению с частными производными второго порядка, называемому уравнением Лапласа.

Функции, удовлетворяющие уравнению Лапласа, называются гармоническими функциями.

Функции $\varphi_1(x,y)$, $\varphi_2(x,y)$ удовлетворяющие уравнению Лапласа и условиям Коши-Римана называются взаимно сопряженными.

Итак, вещественная и мнимая часть аналитической функции являются сопряженными гармоническими функциями.

Гармонические функции встречаются во многих задачах физики и механики. Так, например, температура однородной пластинки, находящейся в тепловом равновесии, электрический потенциал плоского проводника, потенциал скоростей плоского установившегося потока однородной, несжимаемой жидкости и т.д. являются гармоническими функциями декартовых координат $x$ и $y$, т.е. удовлетворяют уравнению Лапласа, в соответствующих областях.

При решении многих задач механики и физики вместо того, чтобы искать гармонические функции и оперировать с ними, ищут аналитические функции, вещественными или мнимыми частями которых являются эти гармонические функции.

Восстановление аналитической функции по ее вещественной или мнимой части

Мы всегда можем построить аналитическую функцию (с точностью до постоянного множителя), для которой данная гармоническая функция является или действительной, или мнимой частью. Другую часть (мнимую или действительную) можно восстановить из условий Коши-Римана. Рассмотрим пример восстановления аналитической функции по ее заданной вещественной части, а потом запишем решение подобной задачи в общем виде.

Рассмотрим задачу: Восстановить аналитическую функцию $w=f(z)$, для которой данная функция $u=x^2-y^2+2x$ является вещественной частью.

1. Прежде всего надо помнить, что вещественная $u(x,y)$ и мнимая $v(x,y)$ части аналитической функции должны быть гармоническими, т.е. удовлетворять уравнению Лапласа.

2. Теперь найдем $v(x,y)$, используя условия Коши-Римана. $$ \frac<\partial u><\partial x>=\frac<\partial v> <\partial y>\,\, \Rightarrow $$ $$ v=\int\frac<\partial u> <\partial x>dy = 2xy+2y+C(x). $$ $$ \frac<\partial u><\partial y>=-\frac<\partial v> <\partial x>\,\, \Rightarrow $$ $$ -2y=-(2y+C'(x)) \,\, \Rightarrow C(x)=C_1\in \mathbb R_<>. $$ $$ v=2xy+2y+C_1. $$ $$ f(z)=u+\mathbf i y = x^2-y^2+2x +\mathbf i (2xy+2y+C_1)=z^2+2z+\mathbf i C_1. $$

Запишем решение задачи восстановления аналитической функции в общем виде.

Пусть дана гармоническая функция $u(x,y)$. Требуется найти $v(x,y)$, $f(z)=u+\mathbf i v$. Запишем условия Коши-Римана: $$ \frac<\partial v><\partial x>=-\frac<\partial u><\partial y>=P(x,y),\quad \frac<\partial v><\partial y>=\frac<\partial u><\partial x>=Q(x,y). $$ Составим полный дифференциал функции $v$: $$ dv=\frac<\partial v><\partial x>dx+\frac<\partial v><\partial y>dy=P(x,y)dx+Q(x,y)dy. $$ Он является полным, если $P’_y=Q’_x$, то есть $\displaystyle\frac<\partial^2 u><\partial x^2>+\frac<\partial^2 u><\partial y^2>=0$, что выполнено, так как данная функция $u(x,y)$ является гармонической. Тогда $$ v=\int\limits_<(x_0,y_0)>^ <(x,y)>P(x,y)dx+Q(x,y)dy+C, $$

$$ (x_0,y_0)\in D, \quad (x,y)\in D, $$ $$ f(z)=u(x,y)+\mathbf i v(x,y). $$ Так как дифференциал $dv$ — полный, то интеграл $\int\limits_<(x_0,y_0)>^ <(x,y)>Pdx+dy$ не зависит от пути интегрирования, если $D$ — односвязная область. При вычислении такого криволинейного интеграла удобно идти параллельно координатным осям. Например, сначала от точки $(x_0,y_0)$ вдоль оси $x$ до точки $(x,y_0)$, потом вдоль оси $y$ до точки $(x,y)$: $$ v(x,y)=\int\limits_^x P(x,y_0)dx+\int\limits_^y Q(x,y)dy +C= $$ $$ =-\int\limits_^x\frac<\partial u><\partial y>dx+\int\limits_^y \frac<\partial u><\partial x>dy +C. $$

Если дана гармоническая функция $v(x,y)$ и требуется найти аналитическую функцию $f(z)=u+\mathbf i v$, аналогично придем к криволинейному интегралу: $$ u(x,y)=\int\limits_<(x_0,y_0)>^<(x,y)>\frac<\partial v><\partial y>dx-\frac<\partial v><\partial x>dy +C. $$

Римановы поверхности

Риман предложил рассматривать многозначные функции комплексного переменного как однозначные функции на некоторых многолистных поверхностях.