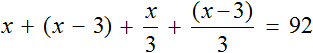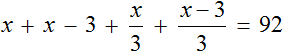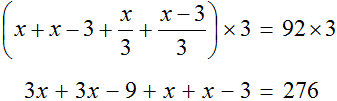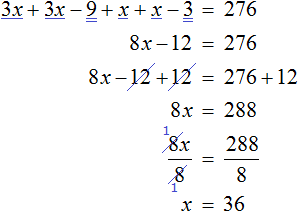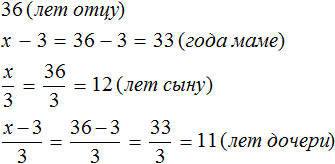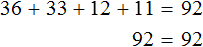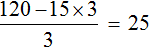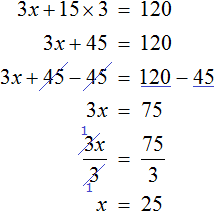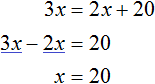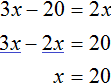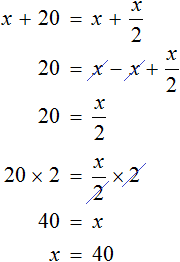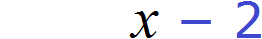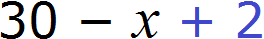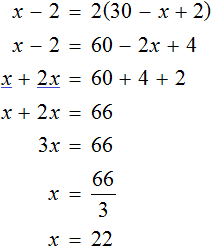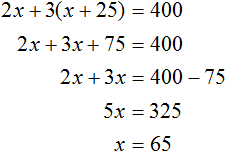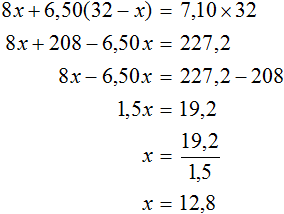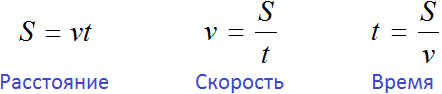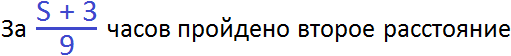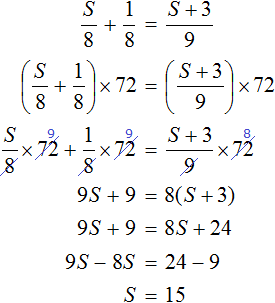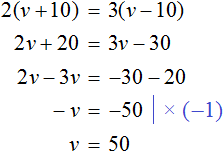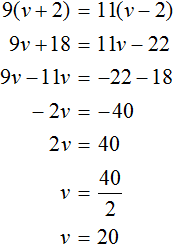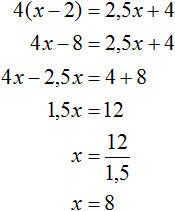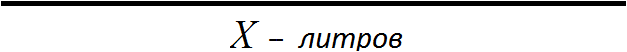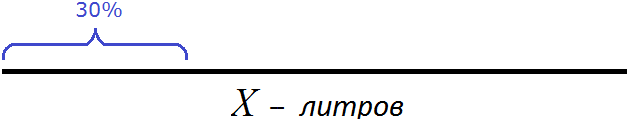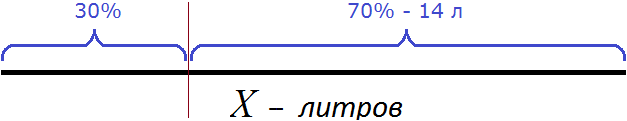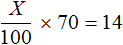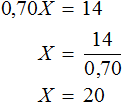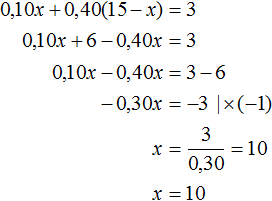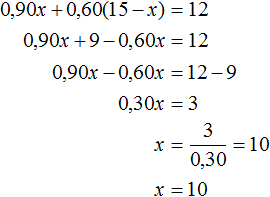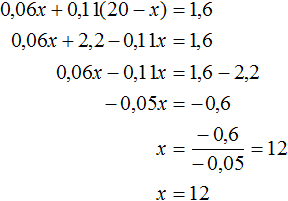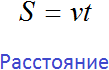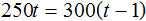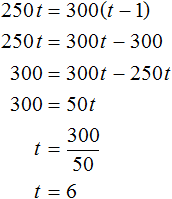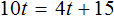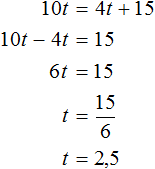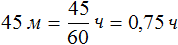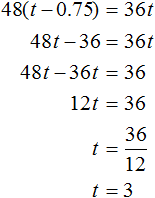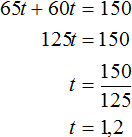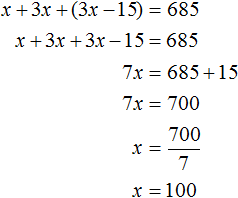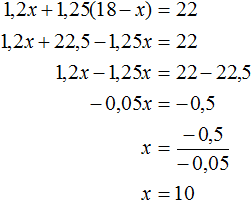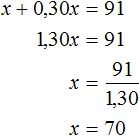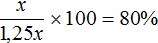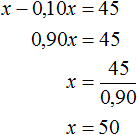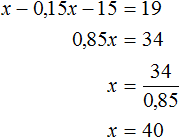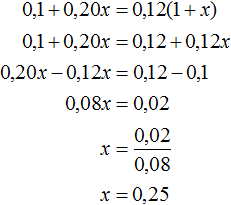Я с помощью уравнений и теорем

Посредством уравнений, теорем Я уйму всяких разрешил проблем. Посредством уравнений, теорем Я уйму всяких разрешил проблем. — презентация

Презентация была опубликована 8 лет назад пользователемДанила Филатов

Похожие презентации

Презентация на тему: » Посредством уравнений, теорем Я уйму всяких разрешил проблем. Посредством уравнений, теорем Я уйму всяких разрешил проблем.» — Транскрипт:

3 Посредством уравнений, теорем Я уйму всяких разрешил проблем. Посредством уравнений, теорем Я уйму всяких разрешил проблем.

4 Является ли уравнением выражение Является ли уравнением выражение (х + 1)(х – 4) = 0? (х + 1)(х – 4) = 0? Каким наиболее рациональным способом мы можем его решить? Каким наиболее рациональным способом мы можем его решить?

6 Тест Виды квадратных уравнений Ф. И. полноенеполноеприведенноенеприведенноеОбщий балл 1. х 2 + 8х +3 = х = 0 3. х 2 – 3х = 0 4. –х 2 + 2х +4 = х + 6х =0

7 Критерий оценивания: Нет ошибок – 5 б. Нет ошибок – 5 б. 1 – 2 ош. – 4б. 1 – 2 ош. – 4б ош. — 3б ош. — 3б ош. – 2б ош. – 2б. Более 6 ош. – 0 б. Более 6 ош. – 0 б.

8 Решение задач с помощью квадратных уравнений Необходимость решать квадратные уравнения еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения вавилоняне умели решать еще около 2000 лет до н. э. правило решения этих уравнений, изложенное в Вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила. 8 материал подготовлен для сайта matematika.ucoz.com

9 Квадратные уравнения в Древнем Египте Наши познания о древнеегипетской математике основаны главным одразом на двух больших папирусах математического характера и и на нескольких небольших отрывках. Это папирусы Ринда (по имени обнаружившего его ученого) и хранится он в Лондоне, другой большой папирус находится в Москве. Содержащиеся в них математические сведения относятся примерно к 2000г. до н.э. Исчисление «аха» Из берлинского папируса эпохи среднего царства ( г. до н.э.) Исчисление «аха» Из берлинского папируса эпохи среднего царства ( г. до н.э.) Квадрат и другой квадрат, сторона которого есть 1/2+1/4 (1) стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это. (2) Возьми квадрат со стороной 1, и возьми ½+1/4 от 1, то есть ½+1/4 в качестве стороны второй площади. Помножь ½+1/4 на самого себя; это дает ½+1/16. поскольку сторона первой площади взята за 1, а второй за ½+1/4, то сложи обе площади вместе; это дает 1+1/2+1/16. возьми корень отсюда: это будет 1+1/4. возьми корень из данных 100: это будет 10. Сколько раз входит 1+1/4 в 10? Это входит 8 раз. [Далее текст прочесть нельзя] Примечание: (1)Древнеегипетские вычислители использовали дроби вида 1/k, где k-целое положительное число и дроби 2/3.3/4. (2) условие задачи можно записать так:

10 Квадратные уравнения в Древнем Вавилоне Вавилоняне умели решать квадратные уравнения около 2000 лет до н.э., когда в Вавилоне правил царь Хаммурапи. Правило решений совпадает по существу с современным, однако неизвестно каким образом они дошли до этого правила. В клинописных текстах отсутствуют понятие отрицательного числа и общий метод решения квадратных уравнений. «Площадь А, состоящая из суммы двух квадратов, составляет сторона одного из квадратов составляет 2/3 стороны другого квадрата, уменьшенные на 10. каковы стороны квадрата?» Это приводит к уравнениям:, решение которых сводится к решению квадратного уравнения, имеющему положительный корень х=30. В действительности решение записано простым перечислением этапов вычисления: «Возведи в квадрат 10, это дает 100, вычти 100 из 1000; это дает 900…» и т.д. Это приводит к уравнениям:, решение которых сводится к решению квадратного уравнения, имеющему положительный корень х=30. В действительности решение записано простым перечислением этапов вычисления: «Возведи в квадрат 10, это дает 100, вычти 100 из 1000; это дает 900…» и т.д.

11 Квадратные уравнения в Древней Греции Математики Древней Греции использовали для решения линейных и квадратных уравнений метод приложения площадей. Примерами таких задач являются: определение сторон правильных вписанных многоугольников, так называемое «золотое сечение» отрезка, выражение ребер правильных многогранников через диаметр описанного шара и т.д. Метод решения зависел от вида квадратного уравнения. Такие методы давали только один положительный корень. Древние математики понимали необходимость так формулировать условие задачи, чтобы они заведомо имели положительные решения.

12 древнегреческий математик из Александрии Он собирал известные и придумывал новые задачи, а позднее объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть пережили хаос Средних веков и стали источником вдохновения для математиков эпохи Возрождения. Остальные семь книг погибли в результате цепочки трагических событий, которые отбросили математику к временам древних вавилонян. В верхней строке записано уравнение Лист из Арифметики

13 . Впервые ввёл термин «квадратное уравнение» немецкий философ — знаменитый немецкий философ, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.

14 Формулы решения квадратных уравнений в Европе были впервые изложены вКниге об абаке, написанной в 1202 году итальянским математиком Леонардо Фибоначчи. Его книга способствовала распространению алгебраических знаний не только в Италии, но и Германии, Франции и других странах Европы. 14

15 – английский математик, который ввёл термин «дискриминант».

16 Но общее правило решения квадратных уравнений, при всевозможных комбинациях коэффициентов b и c было сформулировано в Европе лишь в 1544 году немецким математиком М.Штифелем. 16

17 Тема урока: «Новое свойство квадратных уравнений»

18 Вы решали квадратные уравнения различными способами: выделением квадрата двучлена, по формуле корней, и каждый раз убеждались в том, что уравнение можно решить легче и быстрее. Сейчас мы познакомимся еще с одним способом решения, который позволит устно и быстро находить корни квадратного уравнения. Дорогие ребята!

19 Назовите коэффициенты в каждом уравнении и найдите сумму коэффициентов. 1) х 2 -5х+1=0; 1) х 2 -5х+1=0; 2) 9х 2 -6х+10=0; 2) 9х 2 -6х+10=0; 3) х 2 +2х-2=0; 3) х 2 +2х-2=0; 4) х 2 -3х-1=0; 4) х 2 -3х-1=0; 5) х 2 +2х-3=0; 5) х 2 +2х-3=0; 6) 5х 2 -8х+3=0; 6) 5х 2 -8х+3=0; Сумма коэффициентов 1-5+1= = = = = = = = = = = =0.

20 Найдите закономерность: 1)в корнях этих уравнений; 2)в соответствии между отдельными коэффициентами и корнями; 3)в сумме коэффициентов. Уравнение Сумма коэффициентов Корни х 2 +4х-5=0; 0 1; -5 3х 2 +3х-6=0; 0 1; -2 5х 2 -8х+3=0; 0 1; 0,6 -7х 2 +2х+5=0; 0 1; -5/7 -2х 2 -5х+7=0 0 1; -3,5

21 Как вы думаете, влияет ли сумма коэффициентов на способ решения квадратного уравнения? Если в квадратном уравнении a+b+c=0, то х 1 =1; х 2 =с/а.

22 Запомните! Если сумма коэффициентов квадратного уравнения равна 0, то один из корней этого уравнения равен 1, а второй – отношению коэффициента а к коэффициенту с.

23 Следствие 2: Следствие 2: Если в квадратном уравнении, то один из корней уравнения равен (-1), а другой равен (-с/а). Доказательство: Рассмотрим уравнение Из условия следует, что

24 Из списка уравнений выберите те, которые решаются с помощью этого свойства.

25 Выполните самостоятельно: Вариант 1Вариант 2 Выполните самостоятельно:

26 Проверьте ответы: Вариант и и -1, и -0, и -16 Вариант 2. 1 и и и -1,2 1 и -1,2 1 и -0,12 1 и -0,12 1 и -9 1 и -9

27 Согласны ли вы с тем, что: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнения выяснить, какой из них короче и эффективнее» Сойер У. Сойер У.

28 Домашнее задание: Задание 1. Подумайте ! Каковы корни квадратного уравнения Каковы корни квадратного уравнения ax 2 +bx+c=0, ax 2 +bx+c=0, если a-b+c=0 если a-b+c=0

29 Для составления картины деятельности на уроке ответьте на следующие вопросы: Какое новое свойство квадратных уравнений вы узнали сегодня? Какое новое свойство квадратных уравнений вы узнали сегодня? Чем оно полезно? Чем оно полезно? Что вам понравилось и что не понравилось в сегодняшнем уроке? Что вам понравилось и что не понравилось в сегодняшнем уроке? Какие остались вопросы? Какие остались вопросы?

Эти загадочные уравнения

Окружная научная конференция учащихся

Эти загадочные уравнения

Наумов Виктор, ученик 6 класса

ГБОУ СОШ ж.-д. ст. Погрузная

ГБОУ СОШ ж.-д. ст. Погрузная

с. Красный Яр, 2013 г.

· Введение. Актуальность проблемы изучения способов решения

Глава 1. Исторические сведения…………………………………….4-8

Глава 2. Эти загадочные уравнения………………………………..8-15

2.1. Что мне было известно про уравнение………………………..8-9

2.2. Решение простейших уравнений …………………..……

2.3. Что я нового узнал об уравнениях из школьных учебников……………………………………………………………11-15

Глава 3. Что я нового узнал об уравнении из дополнительной

3.1. Тайное становится явным (исследование)………….……… 15-18

3.2. Способы решения уравнений……………………….……….. 18-20

а) Решение уравнений с помощью правила нахождения неизвестной компоненты…………………………………………………….…………..18

б) Решение уравнений методом весов…………………………..18

в) Решение уравнений методом проб и ошибок………………..19

г) Решением уравнений методом перебора……………. 19

3.3 Математические фокусы…………………………………. 21-23

· Список использованной литературы……………………. 25

· Приложения. Задания для моих одноклассников

Введение. Актуальность проблемы

Уравнение – одно из важнейших понятий математики. В большинстве практических и научных задач, где какую-то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить выражение, которым оно удовлетворяет. Так получают уравнение для определения неизвестной величины. Кто и когда придумал уравнения? Кто ввёл неизвестные величины? Как решаются уравнения? Эти проблемные вопросы, думаю, интересны многим, в том числе и мне. Я высказал гипотезу, что существуют какие-то определенные способы решения уравнений и поставил перед собой цель:

• изучить способы решения уравнений

• углубить математические знания по этой теме

• расширить представления о математике как о языке описания окружающего мира

• изучить литературу и систематизировать материал по данной теме

• исследовать свойства преобразования уравнений

• выявить основные доступные способы решения уравнений

• выработать навыки поисково-исследовательской работы

• систематизация изученного материала

• классификация уравнений по способам их решения

Объект исследования: Уравнения

Предмет исследования: Способы решения уравнений

Слова уравнение и равенство имеют один и тот же корень. Да, и на самом деле, уравнение – это равенство, содержащее неизвестную величину, значение которой нужно найти.

Уравнения в школьном курсе математики занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники.

В начальной школе я научился решать самые простые уравнения, в пятом и шестом классах мы уже решали более сложные уравнения, а в старших классах я научусь решать разные виды уравнений. Существует целая наука алгебра, которая изучает различные виды уравнений и способы их решения. С алгеброй, как учебным предметом, мне предстоит встретиться только в седьмом классе.

Но мне не захотелось ждать седьмого класса. Из дополнительной литературы я решил узнать новое, интересное и загадочное об уравнениях. Поэтому тема моей работы «Эти загадочные уравнения».

Глава 1.Исторические сведения

Кто и когда придумал первое уравнение?

Задачи, которые довольно просто мы сегодня можем решить при помощи уравнений, решали хорошо обученные науке мудрецы, чиновники и жрецы ещё в Древнем Вавилоне и Древнем Египте, Древнем Китае, Древней Индии и Древней Греции. Дошедшие до нас источники свидетельствуют, что древние учёные владели какими-то общими приёмами решения задач с неизвестными. Однако ни в одном папирусе, ни на одной глиняной табличке не дано описание приёмов. Авторы лишь изредка снабжают выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты верно нашёл!» В те времена не было ещё общепринятых теперь обозначений неизвестных буквами, а действий – знаками. Древние египтяне для удобства рассуждений придумали специальное слово, обозначающее неизвестное число, но так как у них не было ещё знаков равенства и знаков действий, то записывать уравнения они, конечно, не умели. Уравнения записывались словами.

Но и в «словесной форме» уравнения существенно облегчали решение задач.

Первым придумал обозначение для

неизвестных греческий математик

Диофант, живший в III веке.

Посредством уравнений, теорем

Он уйму всяких разрешал проблем.

И засуху предсказывал, и ливни –

Поистине его познанья дивны.

Его книга «Арифметика» содержала большое количество интересных задач, её изучали математики всех поколений. Книга сохранилась до наших дней и переведена на русский язык.

Во времена Диофанта языком науки был греческий. Но греки ещё не знали цифр и обозначали числа при помощи букв своего алфавита. Первые девять букв: обозначали числа от 1 до 9; следующие девять:обозначали числа от 10 до 90; наконец, следующие девять: обозначали числа от 100 до 900. чтобы не ошибиться и не принять число за слово, над буквами, обозначающими число, ставилась чёрточка. Букв в алфавите было 28, одна из них была особой – она обозначалась (сигма концевая), ставилась только в конце слов и числового значения не имела. Вот ею-то Диофант и стал обозначать неизвестную величину, так же как мы обычно обозначаем её буквой х.

Придумав это, Диофант стал двигаться дальше. И вместо слова «получится» или «равняется» стал писать — две первые буквы слова («исос» — равный). Диофант придумал знак и для вычитания – им служила буква (пси), только перевёрнутая. А без знака сложения Диофант обходился довольно просто – слагаемые записывал рядом друг с другом. Придумал Диофант и два основных приёма решения уравнений – перенос неизвестных в одну сторону уравнения и приведение подобных членов. С этими приёмами я познакомлюсь при изучении математики в этом году.

Первым руководством по решению уравнений, получившим широкую известность, стал труд арабского учёного IX века Мухаммеда Бен Мус аль -Хорезми. Об аль – Хорезми известно лишь, что он написал ряд трудов по астрономии и географии. И самое главное – он написал сочинение, которое по-арабски называется «Китаб аль-джебр валь-мукабала» (Книга о восстановлении и противопоставлении). Это сочинение оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки – алгебра. Алгебра – часть математики, которая изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями.

Аль-Хорезми одним из первых стал обращаться с уравнениями так, как торговец обращается с рычажными весами. Пусть, например, имеется равенство 5х – 16 = 20 – 4х. Считая, что оно задаёт равновесие некоторых грузов на чашах весов, торговец вправе заключить, что равенство не изменится, если он на обе чаши добавит одно и то же количество:

было 5х – 16 = 20 – 4х,

стало 5х = 36 – 4х.

После этой операции прибавления одинаковых количеств число 16 исчезло из левой части исходного равенства, зато со знаком плюс оно возникло (восстановилось) в правой части. Точно так же на обе чаши весов можно добавить одно и то же количество 4х:

было 5х = 36 – 4х.,

Опять из правой части равенства выражение 4х пропало, а в левой части оно восстановилось со знаком плюс. Из полученного простого равенства 9х = 36 уже легко вычислить, что х = 4.

Взгляд на уравнение как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным. Равные количества можно не только прибавлять к обеим частям уравнения или вычитать из них. Равенство не нарушится и тогда, когда обе части умножаются или делятся на одно и то же число (если оно не нуль). Главный принцип: если над равными количествами произвести одинаковые действия, то в результате снова получатся равные количества – стал своеобразной «волшебной палочкой», которую обнаружили вдумчивые читатели руководства аль-Хорезми.

Новый великий прорыв в решении уравнений связан с именем французского учёного XVI века Франсуа Виета. Он первым из математиков ввёл буквенные обозначения для неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, у или z) мы обязаны соотечественнику Виета – Рене Декарту.

Таким образом, решению уравнений уделялось всегда большое внимание. В древности считалось, что уравнения связаны с тайной, которую нужно разгадать, найдя значение неизвестной величины. Людей, которые могли решать уравнения, считали мудрецами, посвященными в эту тайну, так как уравнения были связаны с решением житейских проблем.

Уравнение – это золотой ключ, открывающий все математические сезамы» С. Коваль

Сезам – заклинание в арабской сказке, силой которого раскрывалась тайная сокровищница.

Глава 2. Эти загадочные уравнения.

2.1.Что мне было известно про уравнение

В учебнике «Математика – 4, часть 2» в разделе «Справочный материал» на странице 92 про уравнение можно прочитать следующее:

« Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Неизвестное число в таком равенстве обозначают латинской буквой (например, х, а, b и др.). Решить уравнение – значит найти такое значение буквы, чтобы равенство стало верным. Например: 15 + х = 18 – уравнение. х = 3 – решение уравнения, так как 15 + 3 = 18 – верное равенство».

В учебнике Виленкина «Математика – 5», в п.10 на страницах 58-59 мы прочтём про уравнение почти то же самое.

Задача. На левой чашке весов лежит арбуз и гиря в 2 кг, а на правой чашке – гиря в5 кг. Весы находятся в равновесии. Чему равна масса арбуза?

Решение. Обозначим неизвестную массу арбуза буквой х. Так как весы находятся в равновесии, то должно выполняться равенство х + 2 = 5.

Нужно найти такое значение х, при котором выполняется это равенство. По смыслу вычитания таким значением будет разность чисел 5 и 2, то есть 3. Значит, масса арбуза равна 3 кг. Пишут: х = 3.

Если в равенство входит буква, то равенство может быть верным при одних значениях этой буквы и неверным при других её значениях.

Например, равенство х + 2 = 5 верно при х = 3 и неверно при х = 4.

Уравнением называют равенство, содержащее букву, значение которой надо найти. Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. (Например, корнем первого уравнения х + 2 = 5 является число3).

Решить уравнение – значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня).

Таким образом, уравнение характеризуется двумя свойствами, которые легко определить на глаз, по внешнему виду: 1) уравнение – это равенство; 2) в этом равенстве есть буква.

2.2. Решение простейших уравнений

Пример 1. Решим уравнение х + 37 = 85.

Решение. По смыслу вычитания неизвестное слагаемое равно разности суммы и другого слагаемого. Поэтому х = 85 – 37 , то есть х = 48.Число 48 является корнем уравнения х + 37 = 85, потому что 48 + 37 = 85.

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Пример 2. Решим уравнение у – 94 = 18.

Решение. По смыслу вычитания у является суммой чисел 18 и 94. Значит, у = 18 + 94, то есть у = 112.Число 112 является корнем уравнения у – 94 = 18, так как верно равенство у – 94 = 18.

Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

Пример 3. Решим уравнение 91 – z = 36.

Решение. По смыслу вычитания число 91 является суммой z и 36 , то есть z + 36 = 91. Из этого уравнения находим неизвестное слагаемое: z = 91 – 36, то есть z = 55.Число 55 является корнем уравнения 91 – z = 36, так как верно равенство 91 – 55 = 36.

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Пример 4. Решим уравнение 35х = 175.

Решение. По смыслу деления имеем: х = 175 : 35, то есть х = 5. Число 5 является корнем уравнения 35х = 175, так как верно равенство 355 = 175.

Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.

Пример 5. Решим уравнение у : 8 = 16.

Решение. По смыслу деления у – произведение множителей 8 и 16. Значит, у = 168, то есть у = 128. Число 128 является корнем уравнения у : 8 = 16, так как верно равенство 128 : 8 = 16.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Пример 6. Решим уравнение 252 : z = 21.

Решение. По смыслу деления число 252 – произведение множителей 21 и z, то есть 21z = 252. Применяя правило нахождения неизвестного множителя, находим: z = 252 : 21, то есть z = 12. Число 12 является корнем уравнения 252 : z = 21, так как верно равенство 252 : 12 = 21.

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Таким образом, при решении этих уравнений я использовал правила нахождения неизвестных компонентов арифметических действий (слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя).

Компонент — слово латинского происхождения, на русский язык переводится как составляющая часть, элемент чего-либо. По этим правилам мы решаем уравнения, начиная со второго класса.

2.3.Что я узнал об уравнениях из школьных учебников

При решении уравнений кроме способа нахождения неизвестного компонента, мы использовали еще второй способ, при котором упрощали выражение, стоящее в левой части уравнения, используя свойства сложения, вычитания и умножения.

Рассмотрю несколько заданий из учебника.

№ 000. Решите двумя способами уравнение:

а) (х + 98) + 14 = 169; б) (35 + у) – 15 = 31 .

Решу первое уравнение двумя способами:

1) сначала найду неизвестное слагаемое х + 98:

а потом найду слагаемое х: х = 155 – 98,

2) сначала упростим выражение, стоящее в левой части уравнения, используя сочетательное свойство сложения

а затем найду неизвестное слагаемое х:

Решу второе уравнение двумя способами:

1) сначала найду неизвестное уменьшаемое 35 + у:

а потом найду слагаемое у: у = 46 – 35,

2) сначала упростим выражение, стоящее в левой части уравнения, используя свойство вычитания: (35 + у) – 15 = 31,

а затем найду неизвестное слагаемое у:

№ 000. Решите уравнение:

а) 3х + 5х + 96 = 1568;

Используя распределительное свойство умножения относительно сложения, упрощу левую часть первого и третьего уравнения, а распределительное свойство умножения относительно вычитания для второго и получу более простые уравнения. а) 8х + 96 = 1568;

б) 208z – 1843 = 11469;

После этого найду неизвестные компоненты: слагаемое, вычитаемое и множитель а) 8х + 96 = 1568,

х = 144. Ответ: 144.

б) 208z – 1843 = 11469,

208z = 11469 + 1843,

у = 167. Ответ: 167.

Еще в пятом классе я научился решать задачи с помощью уравнений.

Решу задачи из нашего учебника.

№ 000. Для школы купили 220 столов и стульев, причем стульев – в 9 раз больше, чем столов. Сколько столов и сколько стульев купили?

Решение. Пусть столов купили х штук, тогда стульев – 9х штук. Всего купили (х + 9х) штук, или 220. Получил уравнение: х + 9х = 220. Решу его. х + 9х = 220,

х = 22. Итак, купили 22 стола, тогда стульев – 229 = 198 .

№ 000(1). Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2, 4.

Решение. Пусть третье число равно х, тогда 2,4х – первое число, а второе х + 0,6 . Среднее арифметическое этих чисел (2,4х + х + 0,6 + х) : 3 по условию задачи равно 2,4. Составлю уравнение и решу его.

(2,4х + х + 0,6 + х) : 3 = 2,4,

4,4х + 0,6 = 2,43,

1,5 –третье число, тогда 1,5 + 0,6 = 2,1 – второе число и 1,52,4 = 3,6 – первое число. Ответ: 3,6; 2,1 и 1,5.

Я провел маленькое исследование и убедился, что в учебнике «Математика – 5» достаточно много заданий, связанных с решением уравнений. Это задания первого вида: «Решите уравнение», «Угадайте корни уравнения» или «Найдите корни уравнения» и задания второго вида: «Решите задачу с помощью уравнения», «Придумайте задачу по уравнению», «Решите задачу».

372, 374, 375, 376, 379, 380, 395, 396, 439, 442, 445, 446, 462, 464, 482, 483, 485, 487, 490, 491, 496, 504, 505, 523, 524, 525 , 551, 568, 569, 570, 574, 576, 592, 593, 614, 615, 635, 639, 647, 660, 707, 727,

878, 1018, 1022, 1036, 1042, 1058, 1107, 1127, 1165, 1210, 1236, 1238, 1251, 1268, 1326, 1329, 1348, 1358, 1362, 1373, 1379, 1389, 1441, 1459, 1489, 1517, 1752, 1817.

373, 377, 397, 410, 440, 447, 484, 486, 489, 512, 526, 571,

572, 577, 578,579, 580, 581, 582, 583, 584, 585, 586, 587, 588, 589, 594, 602, 603, 607, 618, 619, 621, 622, 623, 624, 641, 643, 665, 669, 704, 705, 706, 726, 777, 837, 870, 871, 997, 1126, 1081, 1073, 1105,

1140, 1170, 1253, 1328, 1349, 1350, 1351, 1430,1460, 1461, 1462, 1463, 1490, 1491, 1558, 1559, 15 97, 1647, 1669, 1755, 1756, 1757, 1758, 1760, 1838, 1839, 1840.

То есть, 155 номеров всех заданий учебника, а их 1849, связаны с решением уравнений, то есть = 0, 083 829…. 8,4%. Но если учесть, что в данном учебнике первое задание, связанное с решением уравнения начинается с номера 372, то 1849 – 371 = 1478 и = 0, 10 487… 10%.

Теперь можно сделать вывод, что после изучения темы «Уравнение», каждое 10-е задание учебника требует умений решать уравнения. И это еще раз подчеркивает важность изучения темы «Уравнение»

Глава 3. Что я узнал об уравнении из дополнительной литературы.

3.1.Тайное становится явным (исследование)

Представьте, что в очень лёгком — практиче­ски невесомом — кошельке содержится какое-то количество монет одинакового достоинства. Как узнать, сколько монет в кошельке, не за­глядывая внутрь? Есть очень простой способ: положим кошелёк на одну чашу рычажных ве­сов и уравновесим его монетками на другой чаше. Сколько монет для этого потре­буется — столько же их и в кошельке.

В кошельке семь монет.

Весы — испытанный измерительный инструмент продавцов, химиков и аптекарей приходит на помощь и в чуть более сложном случае.

На левой чаше находящихся в равновесии весов лежат кошелёк с неизвестным числом монет и ещё 5 монет рядом с ним, а на правой чаше — 15 точно таких же монеток. Для того чтобы узнать, сколько монет в кошельке, снимем по 5 монет с обеих чаш — равновесие при этом не нарушится.

Следовательно, внутри кошелька 10 монет

Взгляд на уравнение как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным. В своём сочинении об уравнениях арабский учёный аль – Хорезми замечает, что равные количества можно не только прибавлять к обеим частям уравнения или вычитать из них. Равенство не нарушится и тогда, когда обе части умножаются или делятся на одно и то же число, если оно не равно нулю. Главный принцип: если над равными количествами произвести одинаковые действия, то в результате снова получатся равные количества – стал своеобразной «волшебной палочкой», которую обнаружили вдумчивые читатели руководства аль – Хорезми. Попробую и я воспользоваться этой палочкой, и насколько мне позволяют знания, исследовать и доказать, что аль – Хорезми был прав. Рассмотрю это на простом уравнении.

Проведу исследования и узнаю, на самом ли деле значение х = 19, останется везде одинаковым.

1) Прибавлю к обеим частям уравнения число 12, получу новое уравнение 2х + 28 + 12 = 66 + 12,

воспользуюсь правилом, что два соседних слагаемых можно заменять их суммой, тогда 2х + 40 = 78,

2) Вычту из обеих частей уравнения 16,

чтобы найти неизвестное уменьшаемое (2х + 28) нужно к разности прибавить вычитаемое 2х + 28 = 50 + 16,

1) Умножу обе части уравнения на 3,

(2х + 28) 3= 663,

воспользуюсь правилом, что при умножении суммы на число можно на него умножить каждое слагаемое в отдельности и полученные результаты сложить. 2х 3 + 28 3 = 198, применю правило, что от перестановки множителей произведение не изменяется, и получу 3 2х + 84 = 198,

4) Разделю обе части уравнения на 2,

(2х + 28) : 2 = 66 : 2,

Чтобы разделить сумму на число, можно разделить каждое слагаемое и полученные результаты сложить 2х : 2 + 28 :2 = 66 : 2,

Вывод: значение корня не изменится, если :

— к обеим частям уравнения прибавить или отнять одно и то же число;

— обе части уравнения умножить или разделить на число, неравное нулю.

Эти правила применяются для решения уравнений методом весов.

3.2. Способы решения уравнений.

Из дополнительной литературы я узнал о некоторых способах решения уравнений, с которыми я разобрался, и они оказались мне понятными.

а) Решение уравнений с помощью правила нахождения неизвестного компонента. Решение уравнений этим методом я подробно рассмотрел в главе 2.

б) Решение уравнений методом весов. Решение уравнений методом весов я рассматривал в главе «Исторические сведения».

Решу уравнения таким методом.

а) 4х – 9 = 2х + 11, в) 8х – 10 = 5х + 8,

из обеих частей уравнения из обеих частей уравнения

отнимем по 2х и прибавим 9, отнимем по 5х и прибавим 10,

получим уравнение получим уравнение

х = 20 : 2, х = 18 : 3,

Проверка. 4 10 – 9 = 2 10 + 11, Проверка. 8 6 – 10 = 56 + 8,

40 – 9 = 20 + 11, 48 – 10 = 30 + 8,

Ответ: х = 10. Ответ: х = 6.

Уравнения такого вида мы научимся решать в конце 6 класса, используя правила преобразования выражений, а пока их можно решать методом весов.

в) Решение уравнений методом проб и ошибок

а) Решите уравнение х (х + 3) = 70.

Никакие известные нам правила не помогают найти решение этого уравнения. Попробуем тогда подобрать решение «экспериментально», так называемым методом проб и ошибок.

Нам надо найти такое число х, чтобы значение выражения х(х + 3) было равно 70. Попробуем подставить в это выражение, например, х = 4: 4 (4 + 3) = 28. Мы видим, что выбранное число х слишком мало.

Возьмём теперь х = 6: 6 (6 + 3) = 54, и снова выбранное значение мало, хотя ближе к искомому. А следующая попытка оказывается удачной: при х = 7, имеем 7 (7 + 3) = 70. Значит, при х = 7 данное в условии равенство верно.

Казалось бы, уравнение уже решено, но это не так: ведь может оказаться, что буквенное выражение равно 70 при разных значениях букв. Поэтому нужны некоторые дополнительные рассуждения. Если бы число х было больше 7, то число х + 3 было больше 10, и тогда произведение оказалось бы больше 70. Точно так же число х не может быть меньше 7, иначе произведение будет меньше 70. Следовательно, среди натуральных чисел, есть только одно решение этого уравнения. Ответ: х = 7.

Итак, метод проб и ошибок позволяет найти ответ даже в случае, если уравнение представляет собой новый, не изученный ещё объект. Однако при использовании этого метода следует всегда помнить о том, что подбор одного решения не гарантирует полноты решения. Поэтому требуется дополнительное обоснование того, что найдены все возможные решения, и ни одно не пропущено.

г). Решение уравнений методом перебора.

При решении уравнений методом проб и ошибок мы видели, что простой подбор одного неизвестного числа не даёт уверенности в том, что найдены все искомые значения. В этом состоит существенный недостаток метода проб и ошибок.

Указанного недостатка лишен другой метод решения уравнений – метод полного перебора. При поиске неизвестного числа полным перебором рассматриваются все мыслимые возможности: если мы упустим хотя бы одну, то может оказаться, что именно она и даёт решение уравнение.

Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем просто перебор всех чисел по — порядку.

Например, глядя на уравнение х (х + 3) = 54, можно заметить, что его натуральные корни должны быть делителями числа 54. Значит, х может принимать лишь значения: 1, 2, 3,6, 9, 18, 27, 54. Подставляя эти числа вместо буквы х в уравнение, находим единственный корень х = 6.

Решим еще одно уравнение методом перебора.

Делители числа 20 – 1, 2, 4, 5, 10, 20.

Можно проанализировать и сделать вывод, что среди натуральных решений могут быть только числа большие 3, но меньшие 7. такими числами будут 4 и 5. проверим это.

х = 4, 4( 4 –– 4) = 4 13 = 12.

х = 5, 5(5 – 2)(7 – 5) = 52 2 = 20.

х= 5 – корень уравнения.

Если бы мы не делали анализа, то нам нужно было проверить все 6 чисел. А если число имеет много делителей, то перебор вариантов может оказаться слишком громоздким. Не всегда удаётся подобрать корни уравнения, и тем более доказать единственность решения. Может оказаться, что среди натуральных чисел решения нет, а среди других чисел оно есть.

Именно поэтому математики всегда стремились найти общие решения различных классов уравнений.

3.3. Математические фокусы.

В этом разделе я хочу показать, как с помощью уравнений отгадывать математические загадки и показывать математические фокусы. Основной темой математических фокусов являются угадывание задуманных чисел или результатов действий над ними. Весь секрет фокусов в том, что «отгадчик» знает и умеет использовать особые свойства чисел, а задумавший этих свойств не знает. Математический интерес каждого фокуса и заключается в разоблачении его теоретических основ, которые в большинстве случаев довольно просты, но иногда бывают хитро замаскированы. Рассмотрю один из математических фокусов. Фокусник предложил каждому из публики задумать число. Потом он сказал: «Прибавьте к задуманному числу 5. Теперь из результата вычтите 2. Теперь к результату прибавьте 7». Потом фокусник спросил у желающих, какое число получилось. Услышав ответ, он немедленно объявил каждому, какое число тот задумал. Этот фокус легко разгадать, если умеешь составлять и решать уравнения. Слева запишу задания «фокусника», а справа — выражения, которые он мысленно при этом составляет.

Задумайте число. Обозначаю его буквой х. Прибавьте к нему число 5. Получается число х + 5.

Из результата вычтите 2. Получается (х + 5) – 2.

К результату прибавьте 7. Получается ((х + 5) – 2) + 7. Скажите ваш результат. Допустим, он равен 17.

Приравнивая составленное выражение ((х + 5) – 2) + 7 к 17, получаю уравнение. ((х + 5) – 2) + 7 = 17, Упростим левую часть уравнения, воспользовавшись свойствами сложения и вычитания: ((х + 5) – 2) + 7 = (х + (5 – 2)) + 7 = (х + 3) + 7 = х + (3 + 7) = х + 10. Уравнение теперь получилось совсем простое : х + 10 = 17. Задуманное число х = 17 – 10, х = 7. Такие фокусы нетрудно придумать и самому. Например, эти два фокуса я придумал сам.

· Задумайте число, утройте его. Прибавьте к результату 10, а затем вычтите 1.Скажите, сколько получилось? А я скажу, какое число вы задумали (нужно от названного числа отнять 9 и результат разделить на 3).

· Задумайте число, прибавьте к нему 15, затем вычтите 7 и прибавьте задуманное число. Скажите, сколько получилось? А я скажу, какое число вы задумали (нужно от названного числа отнять 8 и результат разделить на 2).

Удивительной для непосвященных кажется способность отгадывать задуманное другим число. Но если вы узнаете секреты математических фокусов, то сможете не только их показывать, но и придумывать новые. Вы просите товарища задумать любое число, затем отнять от него 1, результат умножить на 2, из произведения вычисть задуманное число и сообщить вам результат. Прибавив к нему число 2, вы отгадаете задуманное. Секрет фокуса становится понятен, если записать предложенные действия в виде алгебраического выражения (x-1)2 – x, где x – задуманное число. Раскрыв скобки, и выполнив действия, мы получим, что это выражение равно x-2. Если ответ равен 23, то задумано число 21. Чтобы угадать задуманное число нужно от результата отнять 2

1.Задумайте число. Умножьте его на 3. К полученному прибавьте полученное разделите на 3. Скажите, сколько получилось?

Решение. (3х + 6) : 3 = х + 2. Чтобы получить задуманное число, нужно от названного числа отнять 2.

2. Задумайте число. Умножьте его на 4. Из полученного вычтите 3. Полученное умножьте на 3, К полученному прибавьте 5. Полученное разделите на 4. К полученному прибавьте 1. Скажите, сколько получилось? Решение. ((4х – 3)3 + 5) : 4 + 1 = (12х – 9 + 5) : 4 + 1 = ( 12х – (9 – 5)) : 4 + +1 = (12х – 4) : 4 + 1 = 3х – 1 + 1 = 3х – (1 – 1) = 3х – 0 = 3х.

Чтобы получить задуманное число, нужно названное число разделить на 3.

3. Задумайте число. Прибавьте к нему 3. Умножьте полученное на 6. Отнимите от полученного 3. Вычтите из полученного результата задуманное число. Полученное разделите на 5. Скажите”, сколько получилось?

Решение (( х + 3) 6 – 3 – х ) : 5 = ( 6х + 18 – 3 – х) : 5 = ( 5х + 15) : 5 = х + 3 . Чтобы получить задуманное число, нужно от названного числа отнять 3.

4. Задумайте любое число. Удвойте его. К полученному прибавьте 3. Полученное число умножьте на задуманное. От полученного результата отнимите задуманное. Полученное разделите на удвоенное задуманное число. Скажите, сколько получилось? Чтобы получить задуманное число, надо от названного числа отнять 1.

Очень эффектно выглядят фокусы на отгадывание даты рождения и возраста зрителей, особенно в малознакомой компании.

Возраст и дата рождения

Порядковый номер месяца рождения нужно умножить на 100 и к получившемуся произведению прибавить число месяца, на которое приходится день рождения. Затем полученную сумму нужно умножить на 2 и к тому, что получится, прибавить 8. Результат нужно умножить на 5, к произведению прибавить 4 и получившуюся сумму умножить на 10. К тому, что получится, остается прибавить полное число лет (возраст), увеличенное на 4. Пусть каждый, выполнивший все эти вычисления, запишет на листочке бумаги свою фамилию, получившееся число и передаст листочек вам. Получив эти листочки, вы по ним каждому можете сказать его возраст и дату рождения. Придется поступать так: из получившегося числа, записанного на листочке, каждый раз вычитайте по 444 и разность разбивайте на грани справа налево по две цифры в каждой. Первая грань справа даст возраст, вторая — число и третья — порядковый номер месяца рождения.

Работа над данной темой помогла узнать мне много нового из истории математики. Мне пришлось рассмотреть дополнительную математическую литературу, чтобы узнать что-то новое про уравнения, и я подтвердил гипотезу, что существуют различные способы решения уравнений.

Просмотрев все учебники по математики с 5 по 11 классы, я убедился в важности выбранной темы. В течение всех лет мы расширяем знания по теме «Уравнения». Я узнал решение более сложных уравнений с помощью правила

нахождения неизвестной компоненты и решение задач на составление уравнений, решал уравнения с применением их свойств, узнал названия уравнений: линейные, квадратные, дробно — рациональные, биквадратные, тригонометрические, иррациональные, показательные и логарифмические уравнений.

Конечно, эти названия мне ни о чём не говорят, но я теперь знаю, какие бывают уравнения, и что со временем я научусь их решать.

Мне было интересно узнать, что уравнения и математические фокусы, которые сейчас могут решать ученики 5-6 класса, в древности были по силам только математикам и мудрецам. И что, используя известные мне свойства сложения и умножения, я смог провести исследования и доказал на простых уравнениях, что значение корня не изменится, если:

— к обеим частям уравнения прибавить или вычесть одно и то же число;

— обе части уравнения умножить или разделить на число, неравное нулю.

Я научился решать более сложные уравнения, используя 4 способа, о них я прочитал в дополнительной литературе. При выполнении работы мне пришлось решить более 120 уравнений. Во время недели математики я показал математические фокусы в 5-х классах и в 3 – 4 классах.

Вместе с моим руководителем мы составили задания для одноклассников. Среди этих заданий есть те, для решения которых достаточно знаний, полученных на уроках. Но есть и такие уравнения, которые решаются новыми способами, о которых я рассказал в работе, то есть требуют дополнительных знаний. Это для тех ребят, кто захочет научиться решать уравнения, используя новые способы.

Я, думаю, что новые знания, которые я получил, пригодятся мне в дальнейшей учёбе. Все цели и задачи, которые я ставил перед собой, я выполнил.

Список использованной литературы

общеобразовательных учреждений. // М.: Мнемозина, 2005.

2. , БеленковаЕ. Ю. Математика 5 класс.

Задания для обучения и развития учащихся.// М.: Интеллект-

3. Математика: Учебник-собеседник для 5 – 6 классов средних школ//

Просвещение, 1989. (Б-ка учителя математики), стр.187

4. , и др. Математика. Учебник для 4 класса нач.

Школы в 2 ч. Ч. 2. (Второе полугодие) – М.: Просвещение, 2005.

5. Энциклопедический словарь юного математика //

Сост. . М.: Педагогика, 1985, стр.345

6. Энциклопедия для детей. Т. 11. Математика // Ред. коллегия:

М. Аксёнова, В. Володин и др. – М.: Аванта, 2005, стр.237

Решение задач с помощью уравнений

Решение задачи обычно свóдится к тому, чтобы путем логических рассуждений и вычислений найти значение какой-нибудь величины. Например, найти скорость, время, расстояние, массу какого-нибудь предмета или количество чего-то.

Такую задачу можно решить с помощью уравнения. Для этого искомое значение обозначают через переменную, затем путем логических рассуждений составляют и решают уравнение. Решив уравнение, производят проверку на то, удовлетворяет ли решение уравнения условиям задачи.

Запись выражений, содержащих неизвестное

Решение задачи сопровождается составлением уравнения к этой задаче. На начальном этапе изучения задач желательно научиться составлять буквенные выражения, описывающие ту или иную жизненную ситуацию. Этот этап не является сложным и его можно изучать в процессе решения самой задачи.

Рассмотрим несколько ситуаций, которые можно записать с помощью математического выражения.

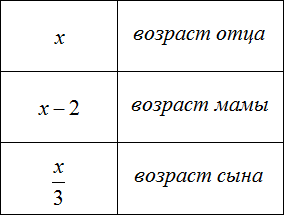
Задача 1. Возраст отца x лет. Мама на два года младше. Сын младше отца в 3 раза. Запишите возраст каждого с помощью выражений.

Решение:

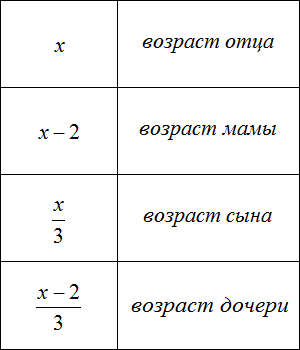
Задача 2. Возраст отца x лет, мама на 2 года младше отца. Сын младше отца в 3 раза, дочь младше матери в 3 раза. Запишите возраст каждого с помощью выражений.

Решение:

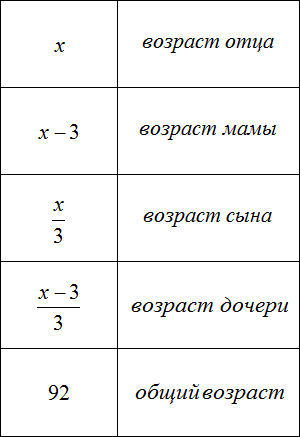
Задача 3. Возраст отца x лет, мама на 3 года младше отца. Сын младше отца в 3 раза, дочь младше матери в 3 раза. Сколько лет каждому, если общий возраст отца, мамы, сына и дочери составляет 92 года?

Решение:

В данной задаче помимо записи выражений, необходимо вычислить возраст каждого члена семьи.

Сначала запишем возраст каждого члена семьи с помощью выражений. За переменную x примем возраст отца, и далее пользуясь этой переменной составим остальные выражения:

Теперь определим возраст каждого члена семьи. Для этого нам нужно составить и решить уравнение. Все компоненты уравнения у нас уже готовы. Осталось только собрать их воедино.

Общий возраст в 92 года получился путем сложения возрастов папы, мамы, сына и дочери:

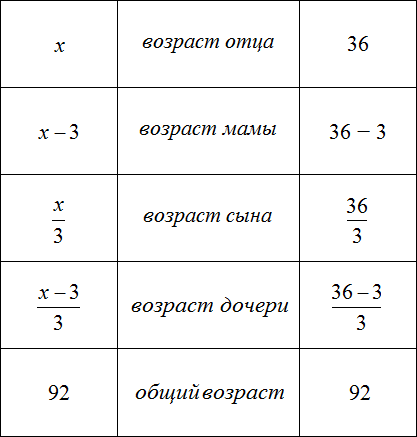
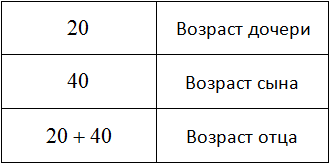
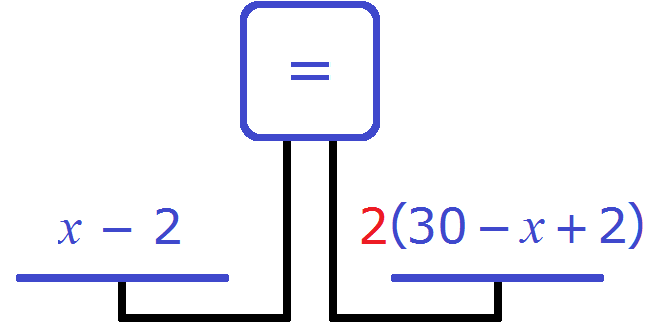
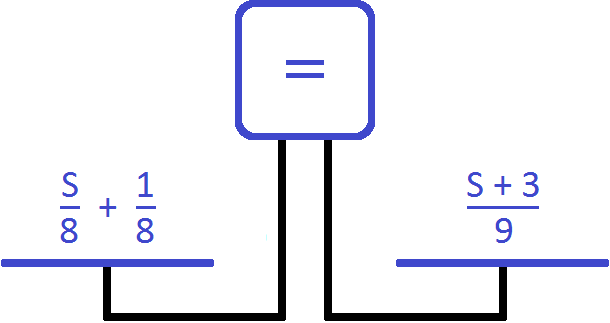
Для каждого возраста мы составили математическое выражение. Эти выражения и будут компонентами нашего уравнения. Давайте соберем наше уравнение согласно данной схеме и таблице, которая была приведена выше. То есть слова папа, мама, сын, дочь заменим на соответствующее им в таблице выражение:

Выражение, отвечающее за возраст мамы x − 3, для наглядности было взято в скобки.

Теперь решим получившееся уравнение. Для начала можно раскрыть скобки там, где это можно:

Чтобы освободить уравнение от дробей, умножим обе части на 3

Решим получившееся уравнение, пользуясь известными тождественными преобразованиями:

Мы нашли значение переменной x . Эта переменная отвечала за возраст отца. Значит возраст отца составляет 36 лет.

Зная возраст отца, можно вычислить возрасты остальных членов семьи. Для этого нужно подставить значение переменной x в те выражения, которые отвечают за возраст конкретного члена семьи.

В задаче было сказано, что мама на 3 года младше отца. Ее возраст мы обозначили через выражение x−3. Значение переменной x теперь известно, и чтобы вычислить возраст мамы, нужно в выражении x − 3 вместо x подставить найденное значение 36

x − 3 = 36 − 3 = 33 года маме.

Аналогично определяется возраст остальных членов семьи:

Проверка:

Задача 4. Килограмм яблок стоит x рублей. Запишите выражение, вычисляющее сколько килограмм яблок можно купить на 300 рублей.

Решение

Если килограмм яблок стоит x рублей, то на 300 рублей можно купить 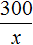килограмм яблок.

Пример. Килограмм яблок стоит 50 рублей. Тогда на 300 рублей можно купить 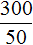, то есть 6 килограмм яблок.

Задача 5. На x рублей было куплено 5 кг яблок. Запишите выражение, вычисляющее сколько рублей стоит один килограмм яблок.

Решение

Если за 5 кг яблок было уплачено x рублей, то один килограмм будет стоит рублей

Пример. За 300 рублей было куплено 5 кг яблок. Тогда один килограмм яблок будет стоит 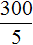, то есть 60 рублей.

Задача 6. Том, Джон и Лео на перемене пошли в столовую и купили по бутерброду и по кружке кофе. Бутерброд стоит x рублей, а кружка кофе — 15 рублей. Определите стоимость бутерброда, если известно, что за всё было уплачено 120 рублей?

Решение

Конечно, данная задача проста как три копейки и ее можно решить не прибегая к уравнению. Для этого из 120 рублей нужно вычесть стоимость трех кружек кофе (15 × 3) , и полученный результат разделить на 3

Но наша цель — составить уравнение к задаче и решить это уравнение. Итак, стоимость бутерброда x рублей. Куплено их всего три. Значит увеличив стоимость в три раза, мы получим выражение описывающее сколько рублей было уплачено за три бутерброда

3x — стоимость трех бутербродов

А стоимость трех кружек кофе можно записать как 15 × 3 . 15 это стоимость одной кружки кофе, а 3 множитель (Том, Джон и Лео), увеличивающий эту стоимость в три раза.

По условию задачи за все уплачено 120 рублей. У нас уже появляется примерная схема, что нужно делать:

Выражения, описывающие стоимость трех бутербродов и трех кружек кофе, у нас уже готовы. Это выражения 3x и 15 × 3 . Пользуясь схемой составим уравнение и решим его:

Итак, стоимость одного бутерброда составляет 25 рублей.

Задача решается верно только в том случае, если уравнение к ней составлено правильно. В отличие от обычных уравнений, по которым мы учимся находить корни, уравнения для решения задач имеют своё конкретное применение. Каждый компонент такого уравнения может быть описан в словесной форме. Составляя уравнение, обязательно нужно понимать для чего мы включаем в его состав тот или иной компонент и зачем он нужен.

Также необходимо помнить, что уравнение это равенство, после решения которого левая часть должна будет равняться правой части. Составленное уравнение не должно противоречить этой идее.

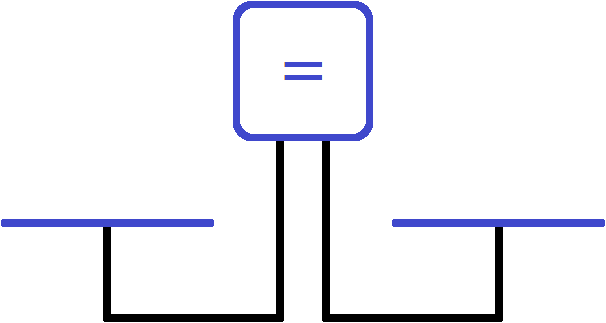
Представим, что уравнение это весы с двумя чашами и экраном, показывающим состояние весов.

В данный момент экран показывает знак равенства. Понятно почему левая чаша равна правой чаше — на чашах ничего нет. Состояние весов и отсутствие на чашах чего-либо запишем с помощью следующего равенства:

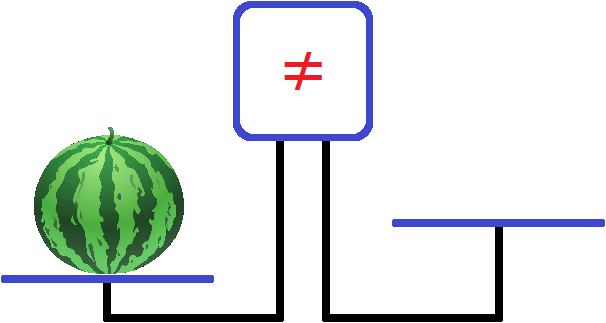
Положим на левую чашу весов арбуз:

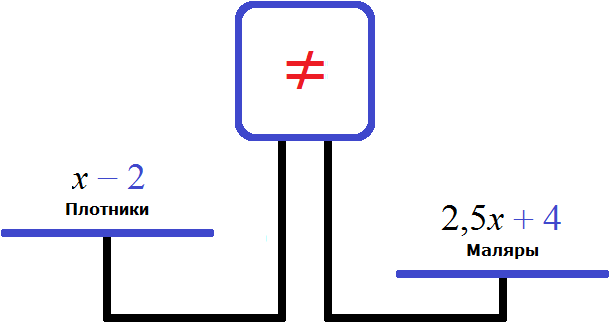
Левая чаша перевесила правую чашу и экран забил тревогу, показав знак не равно ( ≠ ). Этот знак говорит о том, что левая чаша не равна правой чаше.

Теперь попробуем решить задачу. Пусть требуется узнать сколько весит арбуз, который лежит на левой чаше. Но как это узнать? Ведь наши весы предназначены только для проверки равна ли левая чаша правой.

На помощь приходят уравнения. Вспомним, что уравнение по определению есть равенство, содержащее в себе переменную значение которой требуется найти. Весы в данном случае играют роль этого самого уравнения, а масса арбуза это переменная, значение которой нужно найти. Наша цель правильно составить это уравнение. Понимай, выровнять весы так, чтобы можно было вычислить массу арбуза.

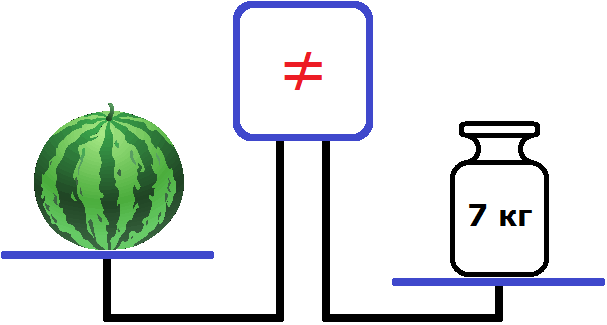
Чтобы выровнять весы, на правую чашу можно положить какой-нибудь тяжелый предмет. Например, положим туда гирю массой 7 кг.

Теперь наоборот правая чаша перевесила левую. Экран по прежнему показывает, что чаши не равны.

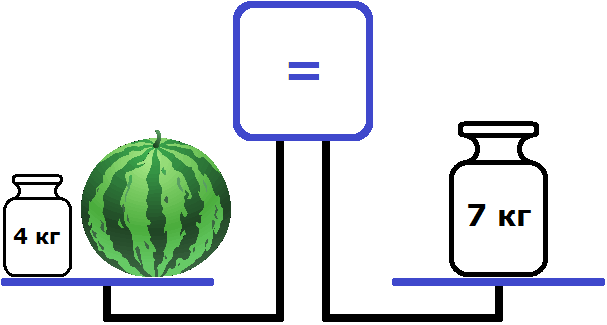
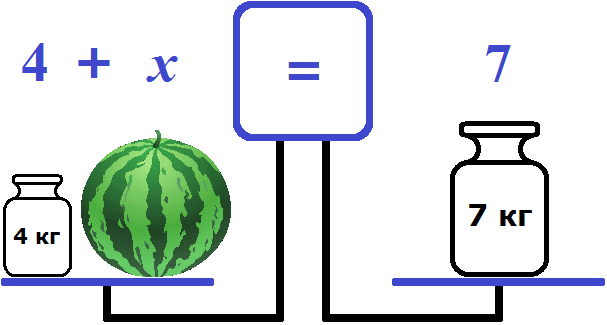
Попробуем на левую чашу положить гирю массой 4 кг

Теперь весы выровнялись. На рисунке видно, что левая чаша на уровне правой чаши. А экран показывает знак равенства. Этот знак говорит о том, что левая чаша равна правой чаше.

Таким образом мы получили уравнение — равенство, содержащее неизвестное. Левая чаша — это левая часть уравнения, состоящая из компонентов 4 и переменной x (массы арбуза), а правая чаша — это правая часть уравнения, состоящая из компонента 7.

Ну и нетрудно догадаться, что корень уравнения 4 + x = 7 равен 3. Значит масса арбуза равна 3 кг.

Аналогично дела обстоят и с другими задачами. Чтобы найти какое-нибудь неизвестное значение, к левой или к правой части уравнения добавляют различные элементы: слагаемые, множители, выражения. В школьных задачах эти элементы бывают уже даны. Остается только правильно структурировать их и построить уравнение. Мы же в данном примере занимались подбором, пробуя гири разной массы, чтобы вычислить массу арбуза.

Естественно, те данные которые даны в задаче сначала нужно привести к виду, при котором их можно включить в уравнение. Поэтому, как говорят «хочешь не хочешь, а думать придётся».

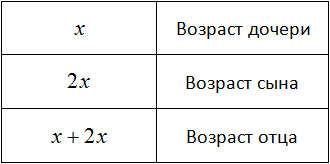
Рассмотрим следующую задачу. Возраст отца равен возрасту сына и дочери вместе. Сын вдвое старше дочери и на двадцать лет моложе отца. Сколько лет каждому?

Возраст дочери можно обозначить через x . Если сын вдвое старше дочери, то его возраст будет обозначаться как 2x . В условии задачи сказано, что вместе возраст дочери и сына равен возрасту отца. Значит возраст отца будет обозначаться суммой x + 2x

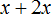
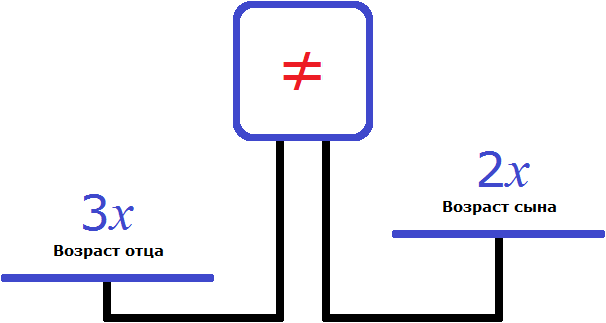
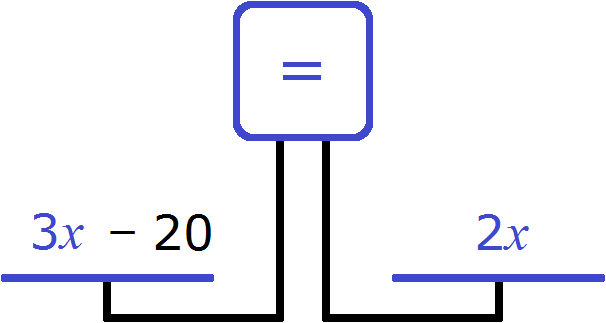
В выражении можно привести подобные слагаемые. Тогда возраст отца будет обозначаться как 3x

Теперь составим уравнение. Нам нужно получить равенство в котором можно найти неизвестное x . Воспользуемся весами. На левую чашу положим возраст отца (3x) , а на правую чашу возраст сына (2x)

Понятно почему левая чаша перевесила правую и почему экран показывает знак ( ≠ ) . Ведь логично, что возраст отца больше возраста сына.

Но нам нужно уравнять весы, чтобы можно было вычислить неизвестное x . Для этого к правой чаше нужно прибавить какое-нибудь число. Какое именно число указано в задаче. В условии было сказано, что сын моложе отца на 20 лет. Значит 20 лет это то самое число, которое нужно положить на весы.

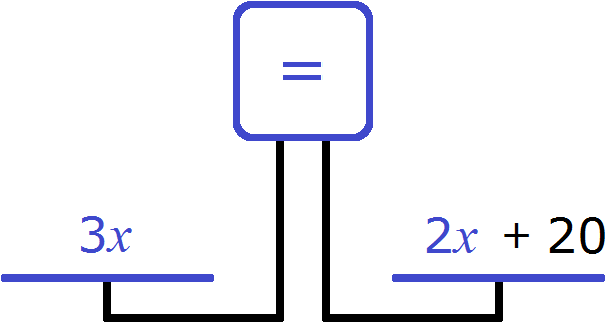
Весы выровнятся, если мы эти 20 лет добавим на правую чашу весов. Иными словами, вырастим сына до возраста отца

Теперь весы выровнялись. Получилось уравнение 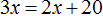, которое решается легко:

В начале решения данной задачи через переменную x мы обозначили возраст дочери. Теперь мы нашли значение этой переменной. Дочери 20 лет.

Далее было сказано, что сын двое старше дочери, значит сыну (20 × 2) , то есть 40 лет.

Ну и наконец вычислим возраст отца. В задаче было сказано, что он равен сумме возрастов сына и дочери, то есть (20 + 40) лет.

Вернемся к середине задачи и обратим внимание на один момент. Когда мы положили на весы возраст отца и возраст сына, левая чаша перевесила правую

Но мы решили эту проблему, добавив на правую чашу еще 20 лет. В результате весы выровнялись и мы получили равенство

Но можно было не добавлять к правой чаше эти 20 лет, а вычесть их из левой. Мы получили бы равенство и в таком случае

В этот раз получается уравнение 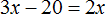. Корень уравнения по прежнему равен 20

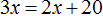
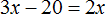
То есть уравнения и являются равносильными. А мы помним, что у равносильных уравнений корни совпадают. Если внимательно посмотреть на эти два уравнения, то можно увидеть что второе уравнение получено путем переноса числа 20 из правой части в левую с противоположным знаком. А это действие, как было указано в предыдущем уроке, не меняет корней уравнения.

Также нужно обратить внимание на то, что в начале решения задачи возрасты каждого члена семьи можно было обозначить через другие выражения.

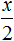
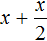
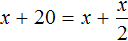
Скажем возраст сына обозначить через x и поскольку он двое старше дочери, то возраст дочери обозначить через (понимай сделать её младше сына в два раза). А возраст отца поскольку он является суммой возрастов сына и дочери обозначить через выражение . Ну и напоследок для построения логически правильного уравнения, к возрасту сына нужно прибавить число 20, ведь отец старше на двадцать лет. В итоге получается совсем другое уравнение . Решим это уравнение

Как видно ответы к задаче не поменялись. Сыну по прежнему 40 лет. Дочери по прежнему 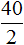лет, а отцу 40 + 20 лет.

Другими словами, задача может решаться различными методами. Поэтому не следует отчаиваться, что не получается решить ту или иную задачу. Но нужно иметь ввиду, что существует наиболее простые пути решения задачи. К центру города можно доехать различными маршрутами, но всегда существует наиболее удобный, быстрый и безопасный маршрут.

Примеры решения задач

Задача 1. В двух пачках всего 30 тетрадей. Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке?

Решение

Обозначим через x количество тетрадей, которое было в первой пачке. Если всего тетрадей было 30, а переменная x это количество тетрадей из первой пачке, то количество тетрадей во второй пачке будет обозначаться через выражение 30 − x . То есть от общего количества тетрадей вычитаем количество тетрадей из первой пачки и тем самым получаем количество тетрадей из второй пачки.

Далее сказано, что если переложить 2 тетради из первой пачки во вторую, то в первой пачке окажется вдвое больше тетрадей. Итак, снимем с первой пачки две тетради

и добавим эти две тетради во вторую пачку

Выражения из которых мы будем составлять уравнение теперь принимают следующий вид:

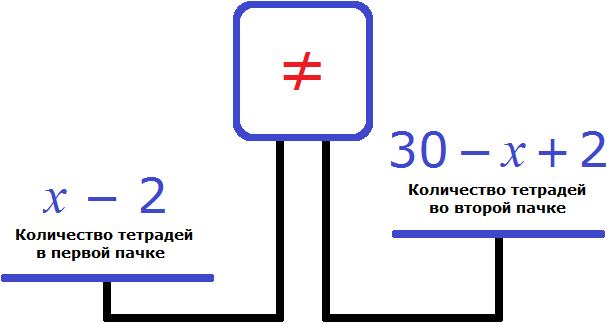
Попробуем составить уравнение из имеющихся выражений. Положим на весы обе пачки тетрадей

Левая чаша тяжелее правой. Это потому, что в условии задачи сказано, что после того как из первой пачки взяли две тетради и положили их во вторую, количество тетрадей в первой пачке стало вдвое больше, чем во второй.

Чтобы выровнять весы и получить уравнение, увеличим правую часть вдвое. Для этого умножим её на 2

Получается уравнение . Решим данное уравнение: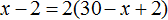

Первую пачку мы обозначали через переменную x . Теперь мы нашли её значение. Переменная x равна 22. Значит в первой пачке было 22 тетради.

А вторую пачку мы обозначали через выражение 30 − x и поскольку значение переменой x теперь известно, то можно вычислить количество тетрадей во второй пачке. Оно равно 30 − 22 , то есть 8 шт .

Задача 2. Два человека чистили картофель. Один очищал в минуту две картофелины, а второй — три картофелины. Вместе они очистили 400 шт. Сколько времени работал каждый, если второй проработал на 25 минут больше первого?

Решение

Обозначим через x время работы первого человека. Поскольку второй человек проработал на 25 минут больше первого, то его время будет обозначаться через выражение

Первый рабочий в минуту очищал 2 картофелины, и поскольку он работал x минут, то всего он очистил 2x картофелин.

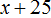
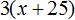
Второй человек в минуту очищал три картофелины, и поскольку он работал минут, то всего он очистил картофелин.

Вместе они очистили 400 картофелин

Из имеющихся компонентов составим и решим уравнение. В левой части уравнения будут картофелины, очищенные каждым человеком, а в правой части их сумма:

В начале решения данной задачи через переменную x мы обозначили время работы первого человека. Теперь мы нашли значение этой переменной. Первый человек работал 65 минут.

А второй человек работал 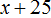минут, и поскольку значение переменной x теперь известно, то можно вычислить время работы второго человека — оно равно 65 + 25 , то есть 90 мин .

Задача из Учебника по алгебре Андрея Петровича Киселева. Из сортов чая составлена смесь в 32 кг. Килограмм первого сорта стоит 8 руб., а второго сорта 6 руб. 50 коп. Сколько килограммов взято того и другого сорта, если килограмм смеси стоит (без прибыли и убытка) 7 руб. 10 коп.?

Решение

Обозначим через x массу чая первого сорта. Тогда масса чая второго сорта будет обозначаться через выражение 32 − x

Килограмм чая первого сорта стоит 8 руб. Если эти восемь рублей умножить на количество килограмм чая первого сорта, то можно будет узнать во сколько рублей обошлись x кг чая первого сорта.

А килограмм чая второго сорта стоит 6 руб. 50 коп. Если эти 6 руб. 50 коп. умножить на 32 − x , то можно узнать во сколько рублей обошлись 32 − x кг чая второго сорта.

В условии сказано, что килограмм смеси стоит 7 руб. 10 коп. Всего же было приготовлено 32 кг смеси. Умножим 7 руб. 10 коп. на 32 мы сможем узнать сколько стоит 32 кг смеси.

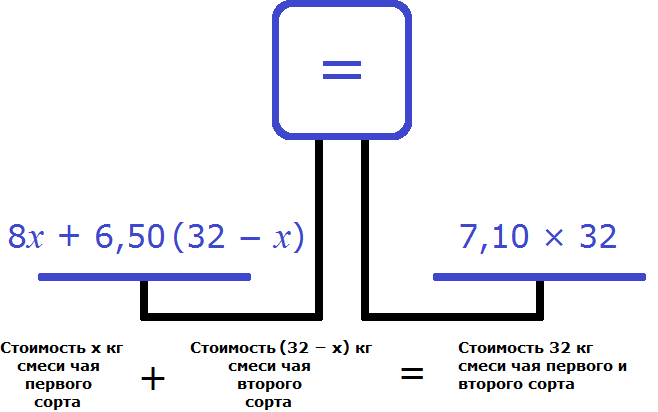
Выражения из которых мы будем составлять уравнение теперь принимают следующий вид:

Попробуем составить уравнение из имеющихся выражений. Положим на левую чашу весов стоимость смесей чая первого и второго сорта, а на правую чашу положим стоимость 32 кг смеси, то есть общую стоимость смеси, в составе которой оба сорта чая:

Получили уравнение 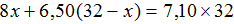. Решим его:

В начале решения данной задачи через переменную x мы обозначили массу чая первого сорта. Теперь мы нашли значение этой переменной. Переменная x равна 12,8. Значит для приготовления смеси было взято 12,8 кг чая первого сорта.

А через выражение 32 − x мы обозначили массу чая второго сорта и поскольку значение переменой x теперь известно, то можно вычислить массу чая второго сорта. Оно равно 32 − 12,8 то есть 19,2 . Значит для приготовления смеси было взято 19,2 кг чая второго сорта.

Задача 3. Велосипедист проехал некоторое расстояние со скоростью 8 км/ч. Возвратиться он должен был другой дорогой, которая была на 3 км длиннее первой, и, хотя возвращаясь, ехал со скоростью 9 км/ч, он употребил времени на минут более. Как длинны были дороги?

Решение

Некоторые задачи могут затрагивать темы, которые человек возможно не изучал. Данная задача относится к такому кругу задач. В ней затрагиваются понятия расстояния, скорости и времени. Соответственно, чтобы решить подобную задачу, нужно иметь представление о тех вещах, о которых говорится в задаче. В нашем случае, надо знать что представляет собой расстояние, скорость и время.

В задаче нужно найти расстояния двух дорог. Мы должны составить уравнение, которое позволит вычислить эти расстояния.

Вспомним, как взаимосвязаны расстояние, скорость и время. Каждая из этих величин может быть описана с помощью буквенного уравнения:

Правую часть одного из этих уравнений мы будем использовать для составления своего уравнения. Чтобы узнать какую именно, нужно вернуться к тексту задачи и обратить внимание на следующий момент:

Следует обратить внимание на момент, где велосипедист на обратном пути употребил времени на минут более. Эта подсказка указывает нам, что можно воспользоваться уравнением , а именно его правой частью. Это позволит нам составить уравнение, которое содержит переменную S .

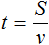
Итак, обозначим длину первой дороги через S . Этот путь велосипедист проехал со скоростью 8 км/ч . Время за которое он преодолел этот путь будет обозначаться выражением , поскольку время это отношение пройденного расстояния к скорости

Обратная дорога для велосипедиста была длиннее на 3 км . Поэтому её расстояние будет обозначаться через выражение S + 3 . Эту дорогу велосипедист проехал со скоростью 9 км/ч . А значит время за которое он преодолел этот путь будет обозначаться выражением .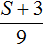

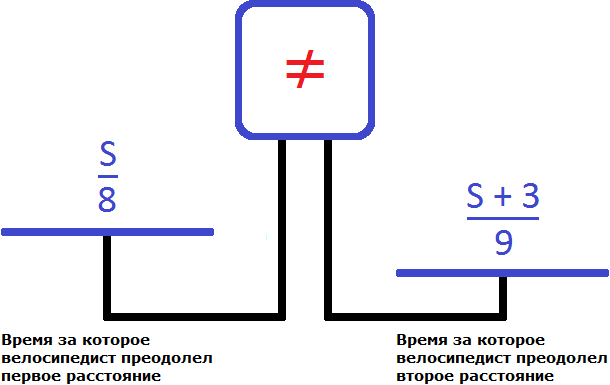
Теперь составим уравнение из имеющихся выражений

Правая чаша тяжелее левой. Это потому, что в задаче сказано, что на обратную дорогу велосипедист затратил времени на больше.

Чтобы уравнять весы прибавим к левой части эти самые минут. Но сначала переведем минуты в часы, поскольку в задаче скорость измеряется в километрах в час, а не в метрах в минуту.

Чтобы минут перевести в часы, нужно разделить их на 60

минут составляют часа. Прибавляем эти часа к левой части уравнения:

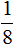
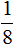
Получается уравнение 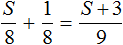. Решим данное уравнение. Чтобы избавиться от дробей, обе части части можно умножить на 72. Далее пользуясь известными тождественными преобразованиями, найдем значение переменной S

Через переменную S мы обозначали расстояние первой дороги. Теперь мы нашли значение этой переменной. Переменная S равна 15. Значит расстояние первой дороги составляет 15 км.

А расстояние второй дороги мы обозначили через выражение S + 3 , и поскольку значение переменной S теперь известно, то можно вычислить расстояние второй дороги. Это расстояние равно сумме 15 + 3 , то есть 18 км .

Задача 4. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2 ч пройдет столько же, сколько вторая за 3 ч. С какой скоростью идут автомашины?

Решение

Обозначим через v скорость каждой машины. Далее в задаче приводятся подсказки: скорость первой машины увеличить на 10 км/ч, а скорость второй — уменьшить на 10 км/ч. Воспользуемся этой подсказкой

Далее говорится, что при таких скоростях (увеличенных и уменьшенных на 10 км/ч) первая машина пройдет за 2 часа столько же расстояния сколько вторая за 3 часа. Фразу «столько же» можно понимать как «расстояние, пройденное первой машиной, будет равно расстоянию, пройденному второй машиной».

Расстояние как мы помним, определяется по формуле 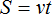. Нас интересует правая часть этого буквенного уравнения — она позволит нам составить уравнение, содержащее переменную v .

Итак, при скорости v + 10 км/ч первая машина пройдет 2(v+10) км , а вторая пройдет 3(v − 10) км . При таком условии машины пройдут одинаковые расстояния, поэтому для получения уравнения достаточно соединить эти два выражения знаком равенства. Тогда получим уравнение 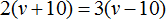. Решим его:

В условии задачи было сказано, что машины идут с одинаковой скоростью. Мы обозначили эту скорость через переменную v . Теперь мы нашли значение этой переменной. Переменная v равна 50. Значит скорость обеих машин составляла 50 км/ч.

Задача 5. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

Решение

Обозначим через v собственную скорость теплохода. Скорость течения реки равна 2 км/ч. По течению реки скорость теплохода будет составлять v + 2 км/ч , а против течения — (v − 2) км/ч .

В условии задачи сказано, что за 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Фразу «тот же путь» можно понимать как «расстояние, пройденное теплоходом по течению реки за 9 часов, равно расстоянию, пройденному теплоходом против течения реки за 11 часов». То есть расстояния будут одинаковыми.

Расстояние определяется по формуле 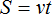. Воспользуемся правой частью этого буквенного уравнения для составления своего уравнения.

Итак, за 9 часов по течению реки теплоход пройдет 9(v + 2) км , а за 11 часов против течения — 11(v − 2) км . Поскольку оба выражения описывают одно и то же расстояние, приравняем первое выражение ко второму. В результате получим уравнение 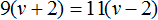. Решим его:

Значит собственная скорость теплохода составляет 20 км/ч.

При решении задач полезной привычкой является заранее определить на каком множестве ищется для неё решение.

Допустим, что в задаче требовалось найти время, за которое пешеход преодолеет указанный путь. Мы обозначили время через переменную t , далее составили уравнение, содержащее эту переменную и нашли её значение.

Из практики мы знаем, что время движения объекта может принимать как целые значения, так и дробные, например 2 ч, 1,5 ч, 0,5 ч. Тогда можно сказать, что решение данной задачи ищется на множестве рациональных чисел Q, поскольку каждое из значений 2 ч, 1,5 ч, 0,5 ч может быть представлено в виде дроби.

Поэтому после того, как неизвестную величину обозначили через переменную, полезно указать к какому множеству эта величина принадлежит. В нашем примере время t принадлежит множеству рациональных чисел Q

Ещё можно ввести ограничение для переменной t , указав что она может принимать только положительные значения. Действительно, если объект затратил на путь определенное время, то это время не может быть отрицательным. Поэтому рядом с выражением t ∈ Q укажем, что её значение должно быть больше нуля:

Если решив уравнение, мы получим отрицательное значение для переменной t , то можно будет сделать вывод, что задача решена неправильно, поскольку это решение не будет удовлетворять условию t ∈ Q , t > 0 .

Ещё пример. Если бы мы решали задачу в которой требовалось найти количество человек для выполнения той или иной работы, то это количество мы обозначили бы через переменную x . В такой задаче решение искалось бы на множестве натуральных чисел

Действительно, количество человек является целым числом, например 2 человека, 3 человека, 5 человек. Но никак не 1,5 (один целый человек и половина человека) или 2,3 (два целых человека и еще три десятых человека).

Здесь можно было бы указать, что количество человек должно быть больше нуля, но числа входящие во множество натуральных чисел N сами по себе являются положительными и большими нуля. В этом множестве нет отрицательных чисел и числа 0. Поэтому выражение x > 0 можно не писать.

Задача 6. Для ремонта школы прибыла бригада в которой было в 2,5 раза больше маляров, чем плотников. Вскоре прораб включил в бригаду еще четырех маляров, а двух плотников перевел на другой объект. В результате маляров в бригаде оказалось в 4 раза больше чем плотников. Сколько маляров и сколько плотников было в бригаде первоначально

Решение

Обозначим через x плотников, прибывших на ремонт первоначально.

Количество плотников является целым числом, большим нуля. Поэтому укажем, что x принадлежит множество натуральных чисел

Маляров было в 2,5 раза больше, чем плотников. Поэтому количество маляров будет обозначаться как 2,5x .

Далее говорится, что прораб включил в бригаду еще четырех маляров, а двух плотников перевел на другой объект. Сделаем для своих выражений тоже самое. Уменьшим количество плотников на 2

А количество маляров увеличим на 4

Теперь количество плотников и маляров будут обозначаться через следующие выражения:

Попробуем составить уравнение из имеющихся выражений:

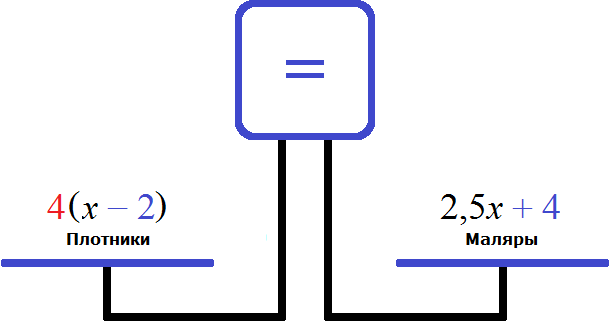
Правая чаша больше, поскольку после включения в бригаду ещё четырёх маляров, и перемещения двух плотников на другой объект, количество маляров в бригаде оказалось в 4 раза больше чем плотников. Чтобы уравнять весы, нужно левую чашу увеличить в 4 раза:

Получили уравнение 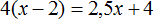. Решим его:

Через переменную x было обозначено первоначальное количество плотников. Теперь мы нашли значение этой переменной. Переменная x равна 8. Значит 8 плотников было в бригаде первоначально.

А количество маляров было обозначено через выражение 2,5 x и поскольку значение переменной x теперь известно, то можно вычислить количество маляров — оно равно 2,5 × 8 , то есть 20 .

Возвращаемся к началу задачи и удостоверяемся, что соблюдается условие x ∈ N. Переменная x равна 8, а элементы множества натуральных чисел N это все числа, начинающиеся с 1, 2, 3 и так далее до бесконечности. В это же множество входит число 8, которое мы нашли.

Тоже самое можно сказать о количестве маляров. Число 20 принадлежит множеству натуральных чисел:

Для понимания сути задачи и правильного составления уравнения, вовсе необязательно использовать модель весов с чашами. Можно использовать и другие модели: отрезки, таблицы, схемы. Можно придумать свою модель, которая хорошо описывала бы суть задачи.

Задача 9. Из бидона отлили 30% молока. В результате в нем осталось 14 л. Сколько литров молока было в бидоне первоначально?

Решение

Искомое значение это первоначальное число литров в бидоне. Изобразим число литров в виде линии и подпишем эту линию как X

Сказано, что из бидона отлили 30% молока. Выделим на рисунке приблизительно 30%

Процент по определению есть одна сотая часть чего-то. Если 30% молока отлили, то остальные 70% остались в бидоне. На эти 70% приходятся 14 литров, указанные в задаче. Выделим на рисунке оставшиеся 70%

Теперь можно составить уравнение. Вспомним, как находить процент от числа. Для этого общее количество чего-то делят на 100 и полученный результат умножают на искомое количество процентов. Замечаем, что 14 литров, составляющих 70% можно получить таким же образом: первоначальное число литров X разделить на 100 и полученный результат умножить на 70. Всё это приравнять к числу 14

Или получить более простое уравнение: 70% записать как 0,70, затем умножить на X и приравнять это выражение к 14

Значит первоначально в бидоне было 20 литров молока.

Задача 9. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?

Решение

Попробуем сначала узнать сколько золота и серебра будет содержáться в 15 кг нового сплава. В задаче сказано, что содержание этих металлов должно быть в отношении 1 : 4, то есть на одну часть сплава должно приходиться золото, а на четыре части — серебро. Тогда всего частей в сплаве будет 1 + 4 = 5, а масса одной части будет 15 : 5 = 3 кг.

Определим сколько золота будет содержáться в 15 кг сплава. Для этого 3 кг умножим на количество частей золота:

Определим сколько серебра будет содержáться в 15 кг сплава:

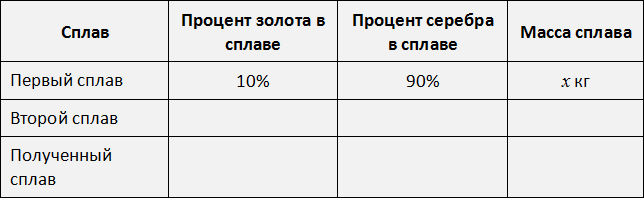
Значит сплав массой 15 кг будет содержать 3 кг золота и 12 кг серебра. Теперь вернёмся к исходным сплавам. Использовать нужно каждый из них. Обозначим через x массу первого сплава, а массу второго сплава можно обозначить через 15 − x

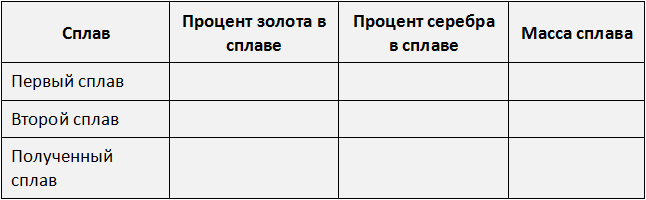
Выразим в процентах все отношения, которые даны в задаче и заполним ими следующую таблицу:

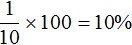
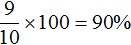
В первом сплаве золото и серебро находятся в отношении 1 : 9. Тогда всего частей будет 1 + 9 = 10 . Из них золота будет , а серебра .

Перенесём эти данные в таблицу. 10% занесём в первую строку в графу «процент золота в сплаве», 90% также занесём в первую строку графу «процент серебра в сплаве», а в последнюю графу «масса сплава» занесём переменную x , поскольку так мы обозначили массу первого сплава:

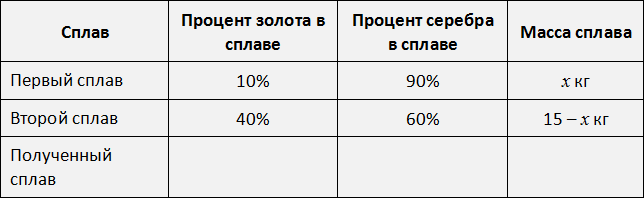
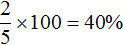
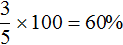
Аналогично поступаем со вторым сплавом. Золото и серебро в нём находятся в отношении 2 : 3. Тогда всего частей будет 2 + 3 = 5. Из них золота будет , а серебра .

Перенесём эти данные в таблицу. 40% занесем во вторую строку в графу «процент золота в сплаве», 60% также занесём во вторую строку графу «процент серебра в сплаве», а в последнюю графу «масса сплава» занесём выражение 15 − x , поскольку так мы обозначили массу второго сплава:

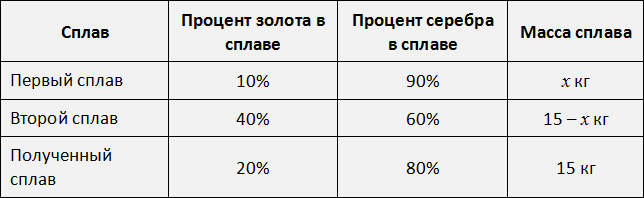
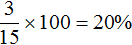
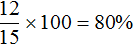
Заполним последнюю строку. Полученный сплав массой 15 кг будет содержать 3 кг золота, что составляет сплава, а серебра будет сплава. В последнюю графу записываем массу полученного сплава 15

Теперь по данной таблице можно составить уравнения. Вспоминаем задачи на концентрацию, сплавы и смеси. Если мы отдельно сложим золото обоих сплавов и приравняем эту сумму к массе золота полученного сплава, то сможем узнать чему равно значение x.

Далее для удобства проценты будем выражать в десятичной дроби.

В первом сплаве золота было 0,10x , а во втором сплаве золота было 0,40(15 − x) . Тогда в полученном сплаве масса золота будет суммой масс золота первого и второго сплавов и эта масса составляет 20% от нового сплава. А 20% от нового сплава это 3 кг золота, вычисленные нами ранее. В результате получаем уравнение 0,10x + 0.40(15 − x) = 3 . Решим это уравнение:

Изначально через x мы обозначили массу первого сплава. Теперь мы нашли значение этой переменной. Переменная x равна 10. А массу второго сплава мы обозначили через 15 − x , и поскольку значение переменной x теперь известно, то можно вычислить массу второго сплава, она равна 15 − 10 = 5 кг .

Значит для получения нового сплава массой 15 кг в котором золото и серебро относились бы как 1 : 4, нужно взять 10 кг первого и 5 кг второго сплава.

Уравнение можно было составить, воспользовавшись и вторым столбцом получившейся таблицы. Тогда мы получили бы уравнение 0,90x + 0.60(15 − x) = 12. Корень этого уравнения тоже равен 10

Задача 10. Имеется руда из двух пластов с содержанием меди в 6% и 11%. Сколько надо взять бедной руды, чтобы получить при смешивании с богатой 20 тонн с содержанием меди 8%?

Решение

Обозначим через x массу бедной руды. Поскольку нужно получить 20 тонн руды, то богатой руды будет взято 20 − x . Поскольку содержание меди в бедной руде составляет 6%, то в x тоннах руды будет содержáться 0,06x тонн меди. В богатой руде содержание меди составляет 11%, а в 20 − x тоннах богатой руды будет содержáться 0,11(20 − x) тонн меди.

В получившихся 20 тоннах руды содержание меди должно составлять 8%. Значит в 20 тоннах руды меди будет содержáться 20 × 0,08 = 1,6 тонн.

Сложим выражения 0,06x и 0,11(20 − x) и приравняем эту сумму к 1,6. Получим уравнение 0,06x + 0,11(20 − x) = 1,6

Решим данное уравнение:

Значит для получения 20 тонн руды с содержанием меди 8%, нужно взять 12 тонн бедной руды. Богатой же будет взято 20 − 12 = 8 тонн.

Задача 11. Увеличив среднюю скорость с 250 до 300 м/мин спортсменка стала пробегать дистанцию на 1 мин быстрее. Какова длина дистанции?

Решение

Длину дистанции (или расстояние дистанции) можно описать следующим буквенным уравнением:

Воспользуемся правой частью этого уравнения для составления своего уравнения. Изначально спортсменка пробегала дистанцию со скоростью 250 метров в минуту. При такой скорости длина дистанции будет описываться выражением 250t

Затем спортсменка увеличила свою скорость до 300 метров в минуту. При такой скорости длина дистанции будет описываться выражением 300t

Заметим, что длина дистанции это величина постоянная. От того, что спортсменка увеличит скорость или уменьшит её, длина дистанции останется неизменной.

Это позволяет нам приравнять выражение 250t к выражению 300t , поскольку оба выражения описывают длину одной и той же дистанции

Но в задаче сказано, что при скорости 300 метров в минуту спортсменка стала пробегать дистанцию на 1 минуту быстрее. Другими словами, при скорости 300 метров в минуту, время движения уменьшится на единицу. Поэтому в уравнении 250t = 300t в правой части время нужно уменьшить на единицу:

Получилось простейшее уравнение. Решим его:

При скорости 250 метров в минуту спортсменка пробегает дистанцию за 6 минут. Зная скорость и время, можно определить длину дистанции:

S = 250 × 6 = 1500 м

А при скорости 300 метров в минуту спортсменка пробегает дистанцию за t − 1 , то есть за 5 минут. Как было сказано ранее длина дистанции не меняется:

S = 300 × 5 = 1500 м

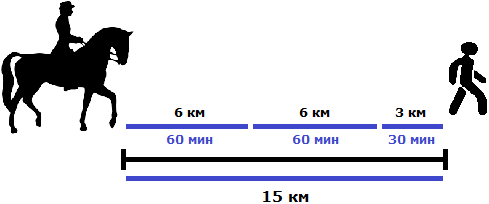
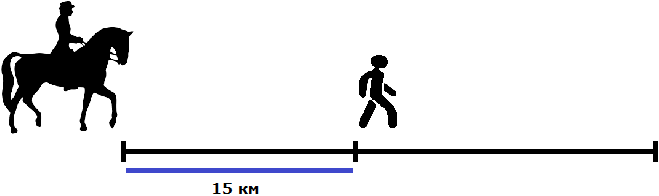
Задача 12. Всадник догоняет пешехода, находящегося впереди него на 15 км. Через сколько часов всадник догонит пешехода, если каждый час первый проезжает по 10 км, а второй проходит только по 4 км?

Решение

Данная задача является задачей на движение. Её можно решить, определив скорость сближения и разделив изначальное расстояние между всадником и пешеходом на эту скорость.

Скорость сближения определяется вычитанием меньшей скорости из большей:

10 км/ч − 4 км/ч = 6 км/ч (скорость сближения)

С каждым часом расстояние в 15 километров будут сокращаться на 6 км. Чтобы узнать, когда оно сократится полностью (когда всадник догонит пешехода), нужно 15 разделить на 6

2,5 ч это два целых часа и половина часа. А половина часа это 30 минут. Значит всадник догонит пешехода через 2 часа 30 минут.

Решим эту задачу с помощью уравнения.

Будем считать, что пешеход и всадник вышли в путь из одного и того же места. Пешеход вышел раньше всадника и успел преодолеть 15 км

После этого вслед за ним в путь вышел всадник со скоростью 10 км/ч. А скорость пешехода составляет только 4 км/ч. Это значит, что всадник через некоторое время догонит пешехода. Это время нам нужно найти.

Когда всадник догонит пешехода это будет означать, что они вместе прошли одинаковое расстояние. Расстояние, пройденное всадником и пешеходом описывается следующим уравнением:

Воспользуемся правой частью этого уравнения для составления своего уравнения.

Расстояние, пройденное всадником, будет описываться выражением 10t . Поскольку пешеход вышел в путь раньше всадника и успел преодолеть 15 км, то расстояние пройденное им будет описываться выражением 4t + 15 .

На момент, когда всадник догонит пешехода, оба они пройдут одинаковое расстояние. Это позволяет нам приравнять расстояния, пройденные всадником и пешеходом:

Получилось простейшее уравнение. Решим его:

Задачи для самостоятельного решения

Решение

Скорости поездов в данной задаче измеряются в километрах в час. Поэтому 45 мин, указанные в задаче, переведем в часы. 45 мин это 0,75 ч

Обозначим время, за которое товарный поезд приезжает в город, через переменную t . Поскольку пассажирский поезд приезжает в этот город на 0,75 ч быстрее, то время его движения будет обозначаться через выражение t − 0,75

Пассажирский поезд преодолел 48(t − 0.75) км, а товарный 36t км. Поскольку речь идет об одном и том же расстоянии, приравняем первое выражение ко второму. В результате получим уравнение 48(t − 0.75) = 36t . Решим его:

Теперь вычислим расстояние между городами. Для этого скорость товарного поезда (36 км/ч) умножим на время его движения t. Значение переменной t теперь известно — оно равно трём часам

Для вычисления расстояния можно воспользоваться и скоростью пассажирского поезда. Но в этом случае значение переменной t необходимо уменьшить на 0,75 поскольку пассажирский поезд затратил времени на 0,75 ч меньше

48 × (3 − 0,75) = 144 − 36 = 108 км

Ответ: расстояние между городами равно 108 км.

Решение

Пусть t время через которое автомобили встретились. Тогда первый автомобиль на момент встречи проедет 65t км, а второй 60t км. Сложим эти расстояния и приравняем к 150. Получим уравнение 65t + 60t = 150

Значение переменной t равно 1,2. Значит автомобили встретились через 1,2 часа.

Ответ: автомобили встретились через 1,2 часа.

Решение

Пусть x рабочих было в первом цехе. Во втором цехе было в три раза больше, чем в первом, поэтому количество рабочих во втором цехе можно обозначить через выражение 3x . В третьем цехе было на 15 рабочих меньше, чем во втором. Поэтому количество рабочих в третьем цехе можно обозначить через выражение 3x − 15 .

В задаче сказано, что всего рабочих было 685. Поэтому можно сложить выражения x, 3x, 3x − 15 и приравнять эту сумму к числу 685. В результате получим уравнение x + 3x + (3x − 15) = 685

Через переменную x было обозначено количество рабочих в первом цехе. Теперь мы нашли значение этой переменной, оно равно 100. Значит в первом цехе было 100 рабочих.

Во втором цехе было 3x рабочих, то есть 3 × 100 = 300 . А в третьем цехе было 3x − 15 , то есть 3 × 100 − 15 = 285

Ответ: в первом цехе было 100 рабочих, во втором — 300, в третьем — 285.

Решение

Пусть x моторов должна была отремонтировать первая мастерская. Тогда вторая мастерская должна была отремонтировать 18 − x моторов .

Поскольку первая мастерская выполнила свой план на 120%, это означает что она отремонтировала 1,2x моторов . А вторая мастерская выполнила свой план на 125%, значит она отремонтировала 1,25(18 − x) моторов.

В задаче сказано, что было отремонтировано 22 мотора. Поэтому можно сложить выражения 1,2x и 1,25(18 − x) , затем приравнять эту сумму к числу 22. В результате получим уравнение 1,2x + 1,25(18 − x) = 22

Через переменную x было обозначено количество моторов, которые должна была отремонтировать первая мастерская. Теперь мы нашли значение этой переменной, она равна 10. Значит первая мастерская должна была отремонтировать 10 моторов.

А через выражение 18 − x было обозначено количество моторов, которые должна была отремонтировать вторая мастерская. Значит вторая мастерская должна была отремонтировать 18 − 10 = 8 моторов.

Ответ: первая мастерская должна была отремонтировать 10 моторов, а вторая — 8 моторов.

Решение

Пусть x рублей стоил товар до повышения цены. Если цена увеличилась на 30% это означает, что она увеличилась на 0,30x рублей. После повышения цены товар начал стоить 91 руб. Сложим x с 0,30x и приравняем эту сумму к 91. В результате получим уравнение x + 0.30x = 91

Значит до повышения цены товар стоил 70 рублей.

Ответ: до повышения цены товар стоил 70 рублей.

Решение

Пусть x — исходное число. Увеличим его на 25%. Получим выражение x + 0,25x . Приведем подобные слагаемые, получим x + 0,25x = 1.25x .

Узнаем какую часть исходное число x составляет от нового числа 1,25x

Если новое число 1,25x считать за 100%, а исходное число x составляет от него 80%, то уменьшив новое число на 20% можно получить исходное число x

Ответ: чтобы получить исходное число, новое число нужно уменьшить на 20%.

Решение

Пусть x — первоначальное число. Увеличим его на 20%. Получим выражение x + 0,20x . Приравняем эту сумму к числу 144, получим уравнение x + 0,20x = 144

Ответ: первоначальное значение числа равно 120.

Решение

Пусть x — первоначальное число. Уменьшим его на 10%. Получим выражение x − 0,10x . Приравняем эту разность к числу 45, получим уравнение x − 0,10x = 45

Ответ: первоначальное значение числа равно 50.

Решение

Пусть x рублей — первоначальная цена альбома. Снизим эту цену на 15%, получим x − 0,15x . Снизим цену ещё на 15 руб., получим x − 0,15x − 15 . После этих снижений альбом стал стоить 19 руб. Приравняем выражение x − 0,15x − 15 к числу 19, получим уравнение x − 0,15x − 15 = 19

Ответ: первоначальная цена альбома составляет 40 руб.

Решение

Если 80% массы теряется, то на оставшиеся 20% будут приходиться 4 т сена. Пусть x тонн травы требуется для получения 4 т сена. Если 4 т будут составлять 20% травы, то можно составить уравнение:

Ответ: для получения 4 т сена, нужно накосить 20 т травы.

Решение

Пусть x кг 20%-го раствора соли нужно добавить к 1 кг 10%-го раствора.

В 1 кг 10%-го раствора соли содержится 0,1 кг соли. А в x кг 20%-го раствора соли содержится 0,20 x кг соли.

После добавления x кг 20%-го раствора в новом растворе будет содержáться 0,12(1 + x) кг соли. Сложим выражения 0,1 и 0,20x , затем приравняем эту сумму к выражению 0,12(1 + x) . В результате получим уравнение 0,1 + 0,20x = 0,12(1 + x)

Ответ: чтобы получить 12%-й раствор соли, нужно к 1 кг 10%-го раствора добавить 0,25 кг 20%-го раствора.

Решение

Пусть x кг первого раствора нужно взять. Поскольку требуется приготовить 25 кг раствора, то массу второго раствора можно обозначить через выражение 25 − x.

В первом растворе будет содержáться 0,20x кг соли, а втором — 0,30(25 − x) кг соли. В полученном растворе содержание соли будет 25 × 0,252 = 6,3 кг. Сложим выражения 0,20x и 0,30(25 − x), затем приравняем эту сумму к 6,3. В результате получим уравнение

Значит первого раствора нужно взять 12 кг, а второго 25 − 12 = 13 кг.

Ответ: первого раствора нужно взять 12 кг, а второго 13 кг.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

44 thoughts on “Решение задач с помощью уравнений”

Вау новый урок. Я рад что вернулись)) После работы обязательно буду учить этот урок.

не смог решить ни одной задачи из примеров решения…