Явная разностная схема для уравнения

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Результаты

Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

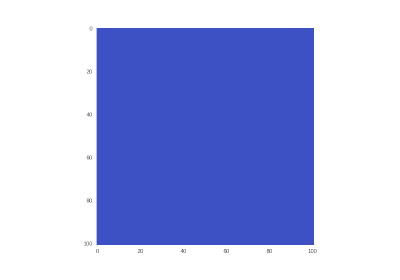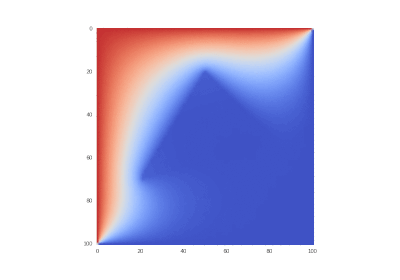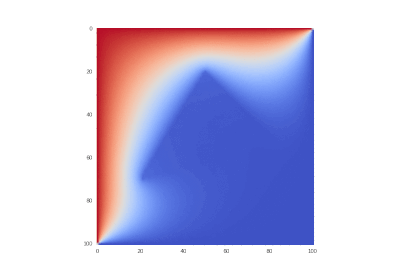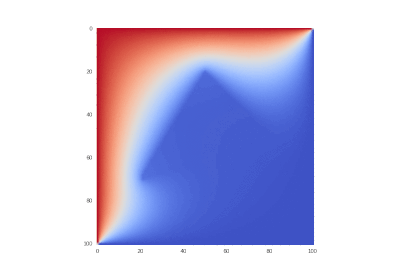
Условие с одним нагревающимся краем:

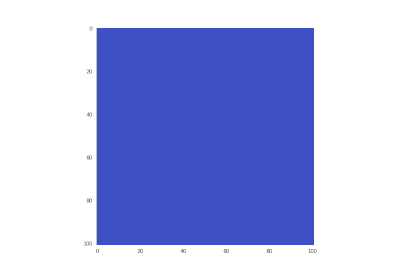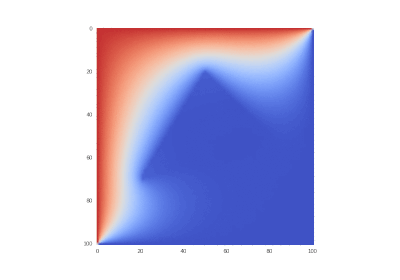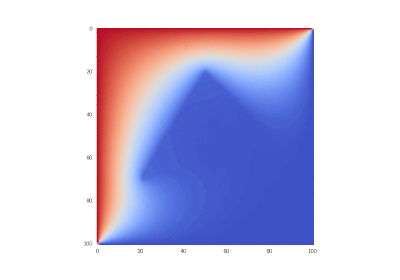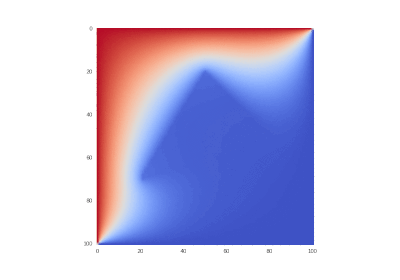
Условие с остыванием изначально нагретой области:

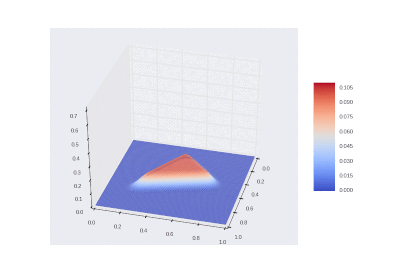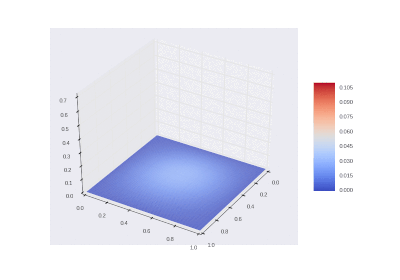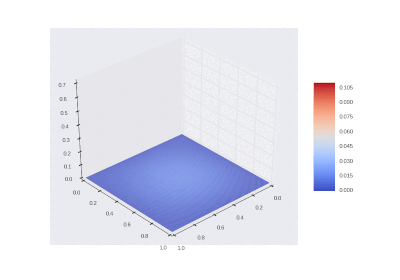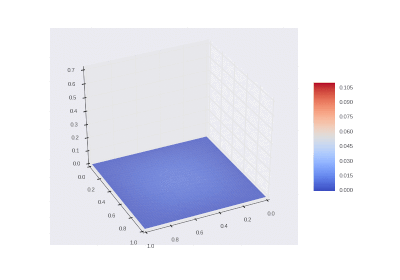
Условие с включением нагрева в области:

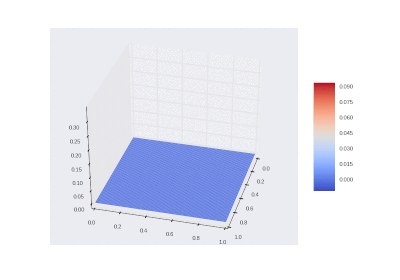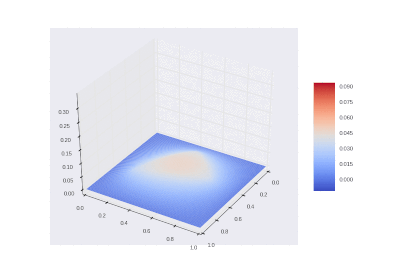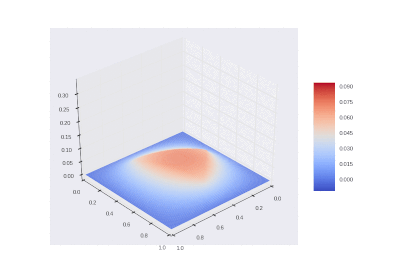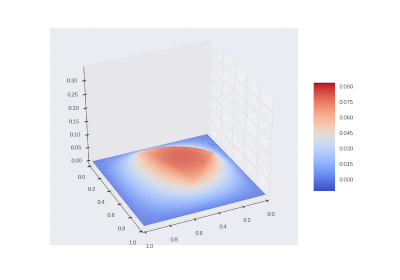
Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

• Intel Core i7 6700HQ 2600 МГц,
• NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

Разностный метод для уравнения колебаний

8.1. Разностный метод для уравнения колебаний

8.1.1. Уравнение колебаний струны. Явная схема

Рассмотрим задачу о малых колебаниях натянутой струны с распределенной по длине нагрузкой f(x, t) (см. рис. 8.1):

(8.11)

(8.12)

(8.13)

Струна совершает плоские колебания, т. е. точки струны перемещаются параллельно плоскости t = 0.

Функция u(x, t) выражает смещение точки x струны в момент времени t от прямолинейной формы.

Начальные условия (8.12) означают следующее. Форма струны в начальный момент времени t = 0 выражается функцией μ(x). Скорость перемещения точки x струны в момент времени t = 0 равна значению функции μ0(x).

Краевые условия (8.13) говорят о том, что левый конец струны с течением времени совершает смещение μ1(t), а правый конец — смещение μ2(t).

Если концы струны закреплены, то μ1(t) = μ2(t) = 0.

Мы предполагаем, что начальные условия (8.12) и краевые условия (8.13) должны быть согласованы между собой в угловых точках, т. е. выполнены условия .

На рис. 8.1 представлен случай, когда , .

Введем сеточную область (рис.8.2, a)). В прямоугольной области зададим точки:

(8.14)

Рассмотрим уравнение (8.11) в точках , , , и заменим производные разностными формулами

, (8.15)

Обозначим через приближенные значения искомой функции в точках . Тогда из уравнения (8.11) получим разностное уравнение (разностную схему), которое аппроксимирует уравнение (8.11) с порядком O(h2 + τ2):

(8.16)

На рис. 8.2 b) изображен шаблон «крест» разностного уравнения (8.16). Разностное уравнение (8.16) связывает значения неизвестной функции на трех слоях (k – 1, k, k + 1).

На слое k = 0 заданы начальные условия (8.12), из которых следует, что

. (8.17)

Чтобы найти значения неизвестной функции на слое k = 1, используем условие для производной ut(x, 0) из (8.12). Для этого построим разложение в ряд Тейлора

. (8.18)

Из уравнения (8.11), учитывая первое условие в (8.12), выразим вторую производную

. (8.19)

Теперь, учитывая условие в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое:

. (8.20)

С учетом (8.13), окончательно получим для приближенных значений искомой функции на первом слое формулы

. (8.21)

Учитывая граничные условия (8.13) из (8.16) выводим формулы для вычисления значений на слоях :

(8.22)

Мы получили явные формулы (8.17), (8.21), (8.22) решения разностной задачи.

Разностная схема называется устойчивой, если она имеет единственное решение и малым изменениям исходных данных отвечают малые изменения решения.

Приведем без доказательства (доказательство можно найти в [9]) следующий факт: для выполнения условия устойчивости разностной схемы (8.16) необходимо и достаточно, чтобы выполнялось условие Куранта cτ 0 находим методом прогонки, последовательными вычислениями в несколько этапов.

2.1. Вычислим правые части (8.26):

(8.29)

2.2. Вычислим прогоночные коэффициенты:

(8.30)

(8.31)

(8.32)

2.3. Вычислим решение ui,k+1:

(8.33)

(8.34)

Отметим преимущества неявной схемы перед явной схемой:

В явной схеме надо выбирать шаги h и τ так, чтобы выполнялось условие устойчивости (условие Куранта) cτ

Явная разностная схема решения одномерного квазилинейного уравнения теплопроводности Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Геренштейн Аркадий Васильевич, Хайрисламов Михаил Зинатуллаевич

Предлагается численный метод решения третьей смешанной задачи для одномерного квазилинейного уравнения теплопроводности параболического типа, основанный на использовании явной разностной схемы . Зависимость коэффициентов уравнения от температуры преодолевается введением новой искомой функции первообразной теплопроводности .

Похожие темы научных работ по математике , автор научной работы — Геренштейн Аркадий Васильевич, Хайрисламов Михаил Зинатуллаевич

EXPLICIT DIFFERENCE SCHEME FOR THE SOLUTION OF ONE-DIMENSIONAL QUASI-LINEAR HEAT CONDUCTIVITY EQUATION

Numerical method for the solution of the third mixed boundary value problem for one-dimensional quasi-linear heat conductivity equation of a parabolic type based on the use of explicit difference scheme is given. Dependence of coefficients on temperature is overcome by the introduction of the new required function that is a primitive integral of conductivity.

Текст научной работы на тему «Явная разностная схема решения одномерного квазилинейного уравнения теплопроводности»

ЯВНАЯ РАЗНОСТНАЯ СХЕМА РЕШЕНИЯ ОДНОМЕРНОГО КВАЗИЛИНЕЙНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ

Л.Б. Геренштеин, М.З. Хаирисламов

Предлагается численный метод решения третьей смешанной задачи для одномерного квазилинейного уравнения теплопроводности параболического типа, основанный на использовании явной разностной схемы. Зависимость коэффициентов уравнения от температуры преодолевается введением новой искомой функции — первообразной теплопроводности.

Ключевые слова: теплопроводность, квазилинейное уравнение теплопроводности, явные разностные схемы, аппроксимация.

В настоящей работе используются идеи, изложенные в работах [1,2], в которых была предложена и обоснована явная устойчивая схема для линейного уравнения теплопроводности.

Рассмотрим следующую постановку третьей смешанной задачи для одномерного однородного квазилинейного уравнения [3]:

Шаблон разностной схемы

йОі(і) .О-і(ґ) — 2О,(і) + Оі+і(і)

і є [0; т], і = 2. N -1.

Аппроксимируем значения (0 и С;+1 (0 с точностью до членов первого порядка малости:

О,- (Г) — 0-1 (0) + ^ (0У, о1+1 (Г) — о1+1 (0) + ^ (0У.

В результате уравнение (3) преобразуется к виду

а 2(иі) ( Оі-і (0) + О,+1(0) + Г &О-І (0) + &О+1 (0) 1 і’

Погрешность аппроксимации оказывается равной О

, даже если производные

(0) вычисляются по формулам первого порядка точности.

Решением уравнения (4) является функция

1 г йО, . + йО,+, > в = О,-1 (0) + О,+1 (0) ‘-2

+ Аі + В, і є [0; т], — А •-

Для обозначения значений сеточной аппроксимации функции С на следующем временном слое будем использовать верхний индекс (+1), а на предыдущем — верхний индекс (-1), на сле-

дующем полуцелом временном слое — I +— I, а на предыдущем полуцелом временном слое —

— (см. рисунок). Запишем теперь разностные аппроксимации для производных ——(0) и

йО ,-1_ (0) = О-12* — О>-12

Окончательно расчетная формула приобретает вид

О(+1 = (О, — В)е п + Ат + В,

1′ «в = О-1 + О+1 — А •- п

Для расчета значений функции С на временном слое і = т, а также для вычисления значений функции в полуцелых слоях по времени можно воспользоваться формулами:

Для применения формул (5)-(7) необходимо по данному значению (7; найти температуру м; та-

кую, что Gj = | с/(д)с/д . В силу монотонности функции С(п) эту задачу можно решить методом 0

деления отрезка пополам (дихотомии).

Аппроксимация краевых условий

Для выполнения краевых условий введены фиктивные узлы с номерами 0 и N +1 (см. рисунок): сначала рассчитываются значения искомой функции во внутренних точках, после чего исходя из краевых условий задаются ее значения в фиктивных узлах.

Перепишем краевое условие на левом конце в задаче (1) с учетом замены искомой функции:

30 =Я1 (и (0, 0) ( — и (0, Г)) + а . (8)

Обозначим через функцию, обратную к функции С, производную ——————-

———, а значение (1(0. і) — полусуммой (1(0. і) = ——. То-

гда условие (8) может быть записано в виде

Обозначив z = G-11 ——— |. из (9) получим уравнение относительно z :

2• G(z)-Л, (z)( -z) = ^ + Qt.

Считаем, что функции q. Для вычисления функций в остальных точках температуры используется ку-сучно-линейная аппроксимация. Поэтому уравнение (10) на каждом промежутке [г;;г;+1],

/’ = 1, т -1 является в общем случае квадратным. Несложные выкладки позволяют записать его в виде

A = q(zi+і) — q(zi) + Mzh±)z¥zA

B = 2 ^ q( zi) zi+1 — q( zi+і) zi Лі (zi+і) -Лі (zt) в + Лі (zi )zi+1 -Лі (z,+1) z,

jWf- q( z, ) z, + q( Z +1) — q (Zi) •

Л (ZI )Zi+1 — Лі (ZI+1)Z± в — — Q

Если г* — корень уравнения (11), принадлежащий промежутку [г,; г1+] \. то искомое значение С0 в фиктивном узле с номером 0 будет равно

Рассуждения для правого конца стержня аналогичны.

Результаты численных расчетов

Для проведения расчетов взята следующая третья смешанная задача:

= Л, (u (0, t)) ( — u (0, t)) + Qt,

= Лг (u(L, t)) (r -u(L, t)) + Qr

где T = 100 c, L = 1 m, % = 22 °C, в, = 1400 °C, Qr = 1400 °C, О, = 105 Дж/(м‘с) , Qr =0 Дж/(м2с), а функции c(u), q(u), Л,(и) и Лг(и) заданы в табл. 1.

Значения входных параметров задачи, являющихся функциями температуры

Параметр Температура, °С

0 100 200 300 400 500 600 700 S00 1000

ф), 10б Дж/(м3-°С) 3,414 3,56S 4,040 4,347 4,S12 5,272 5,SS6 7,2S6 7,21S 7,21S

q(u), Дж/(м3-°С) 22,5 23,4 24,S 2б,7 27,2 27,7 2S,1 2S,6 27 27

Л,(и), Дж/(м2-с-°С) 100 100 110 120 130 140 150 160 170 170

Лг(и), Дж/(м2-с-°С) 100 120 130 140 150 150 150 150 150 150

Результаты численных расчетов по предложенной схеме приведены в табл. 2. В связи с тем, что точное решение задачи (12) неизвестно, проводилось сравнение решения, полученного по предложенной схеме, с решением, полученным по чисто неявной схеме, которая является безусловно сходящейся [3, 5].

Максимальная относительная погрешность решения в сравнении с решением по чисто неявной схеме

Величина шага по времени г, с

Число узлов N 0,01 0,05 0,1 0,5

40 4,7 -10-4 4,5 -10-4 1,52 -10-3 1,72 -10-3

60 1,12 10-3 1,12 10-3 1,19 10-3 2,18 -10-3

80 9,9 -10-4 1,0 10-3 1,06 10-3 2,15 -10-3

100 7,5 -10-4 7,7 -10-4 8,7 -10-4 2,25 -10-3

150 4,2 -10-4 4,7 -10-4 5,9 -10-4 2,43 -10-3

200 2,7 -10-4 3,4 -10-4 5,0 -10-4 2,67 -10-3

1. Геренштейн, А.В. Нагревание круга движущимся теплоисточником / А.В. Геренштейн,

Н. Машрабов // Обозрение прикладной и промышленной математики. — 2008. — Т. 15, №5. -С.870-871.

2. Геренштейн, А.В. Устойчивые явные схемы для уравнения теплопроводности / А.В. Геренштейн, Е.А. Геренштейн, Н. Машрабов // Вестник ЮУрГУ. Серия «Математическое моделирование и программирование». — 2008. — Вып. 1. — № 15(115). — С. 9-11.

3. Самарский, А.А. Теория разностных схем / А.А. Самарский. — М.: Наука, 1989. — 616 с.

4. Годунов, С.К. Разностные схемы / С.К. Годунов, B.C. Рябенький. — М.: Наука, 1977. -440 с.

5. Калиткин, Н.Н. Численные методы / Н.Н. Калиткин; под. ред. А.А. Самарского. — М.: Наука, 1978.- 512 с.

6. Шуп, Т. Решение инженерных задач на ЭВМ / Т. Шуп. — М.: Мир, 1982. — 235 с.

7. Геренштейн, А.В. Расчет температурных полей в цилиндре при действии поверхностных тепловых источников «Тепло 4.0» / А.В. Геренштейн, Н. Машрабов, Е.А. Геренштейн // Государственная регистрация в Отраслевом фонде алгоритмов и программ № 9776, 20.02.2008. — М.: ФГНУ ГКЦИТ, 2008.

8. Машрабов, Н. Расчет температурных полей в цилиндре при действии поверхностных теп-

ловых источников «Тепло 5.0» / Н. Машрабов, А.В. Геренштейн, Е.А. Геренштейн // Свидетельство о государственной регистрации программ для ЭВМ №2008612210, 30.04.2008,

EXPLICIT DIFFERENCE SCHEME FOR THE SOLUTION OF ONE-DIMENSIONAL QUASI-LINEAR HEAT CONDUCTIVITY EQUATION

A.V. Herreinstein1, M.Z. Khayrislamov2

Numerical method for the solution of the third mixed boundary value problem for one-dimensional quasi-linear heat conductivity equation of a parabolic type based on the use of explicit difference scheme is given. Dependence of coefficients on temperature is overcome by the introduction of the new required function that is a primitive integral of conductivity.

Keywords: thermal conductivity, quasi-linear heat conductivity equation, explicit difference schemes, approximation.

1. Herreinstein A.V., Mashrabov N. Nagrevanie kruga dvizhushhimsya teploistochnikom [Circle heating by moving heat source]. Obozrenieprikladnoj ipromyshlennoj matematiki. 2008. Vol. 15, no. 5. pp. 870-871. (in Russ.).

2. Herreinstein A.W., Herreinstein E.A., Mashrabov N. Ustojchivye yavnye skhemy dlya urav-neniya teploprovodnosti [Steady Obvious Schemes for Equation of Heat Conductivity]. Vestnik YuUrGU. Seriya «Matematicheskoe modelirovanie i programmirovanie». 2008. Issue 1. no. 15(115). pp. 9-11. (in Russ.).

3. Samarskij A.A. Teoriya raznostnykh skhem [Theory of difference schemes]. Moscow: Nauka, 1989. 616 p. (in Russ.).

4. Godunov S.K., Ryaben’kij B.C. Raznostnye skhemy [Difference schemes]. M.: Nauka, 1977. 440 p. (in Russ.).

5. Kalitkin N.N. Chislennye metody [Numerical methods]. M.: Nauka, 1978. 512 p. (in Russ.).

6. Shup T. Reshenie inzhenernykh zadach na EVM [The solution of engineering problems with a computer]. Moscow: Mir, 1982. 235 p. (in Russ.).

7. Herreinstein A.V., Mashrabov N., Herreinstein E.A. Raschet temperaturnykh polej v cilindre pri dejstvii poverxnostnykh teplovykh istochnikov «Teplo 4.0» [Calculation of temperature patterns in a cylinder at surface heat sources “Teplo 4.0” effect]. Gosudarstvennaya registraciya v Otraslevom fonde algoritmov iprogramm № 9776. 20.02.2008. Moscow: FGNU GKCIT, 2008. (in Russ.).

8. Mashrabov N., Herreinstein A.V., Herreinstein E.A. Raschet temperaturnykh polej v cilindre pri dejstvii poverkhnostnykh teplovykh istochnikov «Teplo 5.0» [Calculation of temperature patterns in a cylinder at surface heat sources “Teplo 5.0” effect]. Svidetel’stvo o gosudarstvennoj registracii programm dlya EVM №2008612210. 30.04.2008. ROSPATENT [Certificate of state registration of computer program No. 2008612210. 30.04.2008. ROSPATENT], (in Russ.).

Поступила в редакцию 27 декабря 2012 г.

1 Herreinstein Arcady Vasilevich is Cand. Sc. (Physics and Mathematics), Associate Professor, Applied Mathematics Department, South Ural State University.

2 Khayrislamov Mikhail Zinatullaevich is Post-Graduate student, Applied Mathematics Department, South Ural State University.