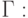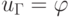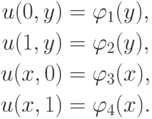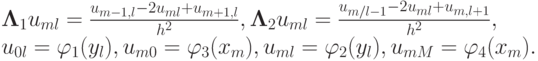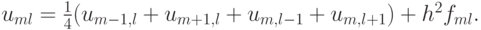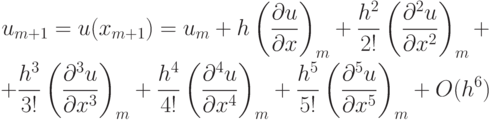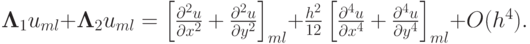Явная схема для уравнения пуассона

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .

6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»

Будем рассматривать двухмерное уравнение Пуассона

в единичном квадрате 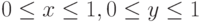с краевыми условиями первого рода на границе расчетной области

( — заданная на границе функция ).

В случае прямоугольной области граничные условия удобно записать в следующем виде:

Для простоты выкладок введем равномерную расчетную сетку с узлами m, y_l> , m, l = 0, 1, . , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию < u_ml >. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.

Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

где h — шаг по координатам, или в операторной форме

Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:

Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.

Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:

Здесь учтено разложение проекции точного решения в ряд Тейлора

и аналогичное разложение для u_{m — 1}.

Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки

Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.

Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.

Уравнение Пуассона и распределение Больцмана (часть 1)

В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:

Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)

Применяя только что введённое понятие градиент, эта формула преобразуется в:

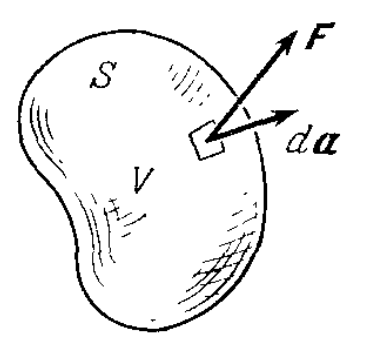
Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно

, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.

Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно

Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:

В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:

Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса

А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):

Комбинируя два последних уравнения, получим:

Вспомним формулу (**) и подставим сюда вместо E потенциал поля

Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен

Перепишем предыдущую формулу в форме лапласиана:

Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не , а коэффициент . Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье

Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.

В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.

20. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений

Ростислав Водосвятский 5 лет назад Просмотров:

1 Варианты заданий 0. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений 0.1. Постановка задачи Рассматривается задача Дирихле для эллиптического уравнения Lu = f(x, ), (x, ) G, (1) u = µ(x, ), (x, ) Γ. () Пусть G = G + Γ = <0 x l x, 0 l >прямоугольник, а Lu = ( p (x, ) u ) + ( q(x, ) u ), (3) x x p (x, ), q(x, ) достаточно гладкие функции, 0 2 так что Lu = L 1 u + L u. Операторы L 1 и L заменим разностными операторами Λ 1 и Λ Здесь Λ 1 u = p i+ 1 j u i+1j u h x u +1 u Λ u = q + 1 h q 1 u u i 1j p i 1 j, (5) h x u u 1 h. (6) Обозначим p i+ 1 j = p(x i + h x /, j ), p i 1 j = p(x i h x /, j ), q + 1 = q(x i, j + h /), q 1 = q(x i, j h /). Λu = Λ 1 u + Λ u, 1 i N x 1, 1 j N 1. Если u(x, ) имеет не менее четырех непрерывных ограниченных в рассматриваемой области G производных по x и по, а p(x, ) и q(x, ) не менее трех, то разностный оператор Λ аппроксимирует дифференциальный L со вторым порядком, т. е. Lu Λu = O( h ), h = h x + h. Итак, решение задачи (1)-() свелось к решению разностной задачи Дирихле (Λ 1 u + Λ u ) = f, 1 i N x 1, 1 j N 1 (7) при граничных условиях u i0 = µ(x i, 0), 0 i N x, u in = µ(x i, l ), 0 i N x, u 0j = µ(0, j ), 0 j N 1, u Nxj = µ(l x, j ), 0 j N 1. (8) 0.3. Метод установления решения задачи Дирихле для уравнения Пуассона Для вычисления решений многих стационарных задач математической физики, описывающих равновесные состояния, рассматриваются последние как результат установления развивающегося во времени процесса, расчет которого оказывается проще, чем прямой расчет равновесного состояния. Рассмотрим вспомогательную нестационарную задачу о распространении тепла u = L 1 u + L u + f(x, ), t (9) u Γ = µ(x, ), u(x,, 0) = u 0 (x, ), где f(x, ) имеет прежний смысл, а u 0 (x, ) произвольно. Поскольку источники тепла f(x, ) и температура на границе µ(x, ) не зависят от времени, то естественно ожидать, что и решение u(x,, t) с течением времени будет меняться все медленнее, распределение температур в пределе при t превратится в равновесное распределение температуры u(x, ), описываемое исходной задачей (1)-(). Надо решать задачу до тех пор, пока ее решение не перестанет меняться в пределах интересующей нас точности. Рассмотрим вначале разностную схему, с помощью которой могла бы решаться задача (7)-(8), но на практике ее не применяют по указанным в п. 0. причинам. 0.. Двухслойная схема с весами Аппроксимируем задачу (9) разностной схемой u k τ = Λ(σ + (1 σ)u k ) + f(x i, j ), 1 (10) 1 При решении стационарных задач методом установления k номер итерации, а τ итерационный параметр, который выбирается из соображений точности аппроксимации и быстроты сходимости.

3 i = 1. N x 1, j = 1. N 1, k = 0, 1. i0 = µ(x i, 0), 0 i N x, in = µ(x i, l ), 0 i N x, 0j = µ(0, j ), 1 j N 1, N xj = µ(l x, j ), 1 j N 1. Решение при k = 0 находится из начального условия в (9) (11) Рассмотрим два варианта значений параметра σ. u 0 = u 0 (x i, j ), i = 0, 1. N x, j = 0, 1. N. а) При σ = 0 получаем явную схему и решение во внутренних узлах сетки вычисляется по формуле = u k + τ(λ 1 u k + Λ u k ) + τf(x i, j ), (1) i = 1. N x 1, j = 1. N 1, k = 0, 1. Схема (1) условно устойчива при τ Ah. Общее число действий при переходе со слоя на слой пропорционально числу узлов сетки, т. е. O(N x N ) схема экономичная. б) При σ = 1 получаем неявную схему. Она устойчива при любых h и τ. Для определения на каждом слое линейную систему получаем τ(λ 1 + Λ ) = u k + τf(x i, j ), (13) i = 1. N x 1, j = 1. N 1, k = 0, 1. Матрица этой системы пятидиагональная и решать систему можно методом матричной прогонки или методом исключения Гаусса, который при учете специального вида матрицы требует O(N xn ) действий, т. е. схема не является экономичной Схема переменных направлений Эта схема сочетает лучшие качества явной схемы экономичность и неявной устойчивость. Наряду с основными значениями u k и uk+1 вводится промежуточное значение /, которое формально можно рассматривать как значение при t = t k+ 1 = t k + τ. Решение задачи в этом случае сводится к решению двух систем вида (1)-(15) с трехдиагональными матрицами. u k+ 1 u k τ/ = Λ 1 u k+ 1 + Λ u k + f(x i, j ), (1) 1 i N x 1, 1 j N 1. 3

4 u k+ 1 τ/ = Λ 1 u k+ 1 + Λ + f(x i, j ), (15) 1 i N x 1, 1 j N 1. k = 0, 1. В граничных узлах решение должно принимать заданные в (11) значения. Схема (1) неявна по направлению x и явна по направлению, а схема (15) явна по направлению x и неявна по направлению, что позволяет использовать для нахождения решения одномерные прогонки. Система (1) с учетом граничных условий (11) может быть записана в следующем виде: u k+ 1 0j = µ(0, j ), где A u k+ 1 i 1j B u k+ 1 + C u k+ 1 i+1j = G k+ 1, 1 i N x 1, u k+ 1 N xj = µ(l x, j ) (16) G k+ 1 = u k τ (Λ u k + f(x i, j )), (17) 1 j N 1. В итоге при каждом 1 j N 1 получили линейную замкнутую систему (N x + 1)-го порядка относительно u k+ 1 0j, u k+ 1 1j. u k+ 1 N xj. Матрица системы 3-х диагональная и решать систему следует методом прогонки. Прогонки осуществляются вдоль строк (рис. ). u k u k+ 1 l Рис. l x x При j = 0, j = N решения находятся из (11): u k+ 1 i0 = µ(x i, 0, t k+ 1 ), 0 i N x, u k+ 1 in = µ(x i, l, t k+ 1 ), 0 i N x. Система (15) с учетом граничных условий (11) может быть записана в следующем виде: i0 = µ(x i, 0), A 1 B + C +1 = G k+1, 1 j N 1, in = µ(x i, l ), где (18) (19) G k+1 = u k+ 1 τ (Λ 1u k+ 1 + f(x i, j )), (0) 1 i N x 1,