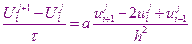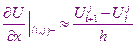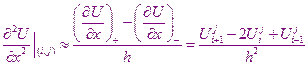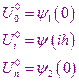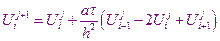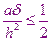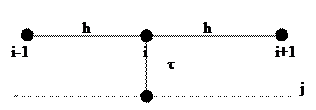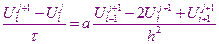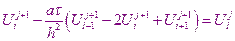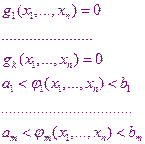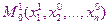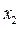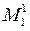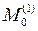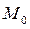Явная схема уравнения теплопроводности что это

Явная разностная схема для уравнения теплопроводности.

Используя шаблон для каждого внутреннего узла области решения апроксимируется уравнение теплопроводности

Используя начальные и граничные условия, находят значения 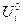сеточной функции во всех узлах на нулевом временном уровне.

Затем с помощью соотношений

находятся значения этих функций во всех внутренних узлах на первом временном уровне, после чего находим значение на граничных узлах

В результате мы находим значение функций во всех узлах на первом временном уровне. После этого с помощью этих соотношений находим все остальные значения и т.д.

В рассматриваемой разностной схеме значения искомой функции на следующем временном уровне находится непосредственно, явно с помощью формулы

Поэтому рассматриваемая разностная схема, использующая этот шаблон, называется явной разностной схемой. Точность её имеет порядок .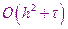

Данная разностная схема проста в использовании, однако она обладает существенным недостатком. Оказывается, что явная разностная схема обладает устойчивым решением только в том случае, если выполняется условие:

Явная разностная схема является условно устойчивой. Если условие не выполняется, то небольшие погрешности вычислений, например, связанные с округлением данных компьютера приводит к резкому изменению решения. Решение становится неприемлемым для использования. Это условие накладывает весьма жесткие ограничения на шаг по времени, что может оказаться неприемлемым из-за значительного увеличения времени счета решения этой задачи.

Рассмотрим разностную схему, использующую другой шаблон

Метод 36

Неявная разностная схема для уравнения теплопроводности.

Подставим в уравнение теплопроводности:

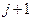
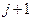
Это соотношение записывается для каждого внутреннего узла на временном уровне и дополняется двумя соотношениями, определяющими значения в граничных узлах. В результате получается система уравнений для определения неизвестных значений функции на временном уровне.

Схема решения задачи следующая:

С помощью начальных и граничных условий находится значение функции на нулевом временном уровне. Затем с помощью этих соотношений и граничных условий строится система линейных алгебраических уравнений для нахождения значения функции на первом временном уровне, после чего опять с помощью этих соотношений строится система, и находятся значения на втором временном уровне и т.д.

Отличие от явной схемы — значения на очередном временном уровне вычисляются не непосредственно с помощью готовой формулы, а находится путем решения системы уравнений, т.е. значения неизвестных находятся неявно путем решения СЛАУ. Поэтому разностная схема называется неявной. В отличие от явной неявная является абсолютно устойчивой.

Тема №9

Задачи оптимизации.

Эти задачи являются одними из важнейших задач прикладной математики. Под оптимизацией понимают выбор наилучшего варианта из всех возможных решений данной задачи. Для этого необходимо сформулировать решаемую задачу как математическую, придав количественный смысл понятиям лучше или хуже. Обычно в процессе решения необходимо найти оптимизируемые значения параметров. Эти параметры называют проектными. А число проектных параметров определяет размерность задачи.

Количественная оценка решения производится с помощью некоторой функции зависящей от проектных параметров. Эта функция называется целевой. Она строится таким образом, чтобы наиболее оптимальное значение соответствовало максимуму(минимуму).

— целевая функция.

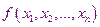
Наиболее просты случаи, когда целевая функция зависит от одного параметра и задаётся явной формулой. Целевых функций может быть несколько.

Например, при проектировании самолёта требуется одновременно обеспечить максимальную надежность, минимальные вес и стоимость и т.д. В таких случаях вводится система приоритетов. Каждой целевой функции ставится в соответствие некоторый целевой множитель в результате получается обобщенная целевая функция(функция компромиссов).

Обычно оптимальное решение ограничено рядом условий связанных с физической функцией задачи. Эти условия могут иметь вид равенств или неравенств

Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследований одного из разделов прикладной математики – математического программирования.

Если целевая функция линейна относительно проектных параметров и ограничения, накладываемые на параметры также линейны, то возникает задача линейного программирования. Рассмотрим методы решения одномерной задачи оптимизации.

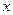
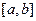
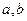
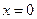
Требуется найти значения на при которых целевая функция имеет максимальное значение. Если целевая функция задана аналитически и может быть найдено выражение для её производных, то оптимальное решение будет достигаться либо на концах отрезка, либо в точках в которых производная обращается в ноль. Это критические точки и . Необходимо найти значения целевой функции во всех критических точках и выбрать максимальное.

В общем случае для нахождения решения применяют различные методы поиска. В результате происходит сужение отрезка содержащего оптимальное решение.

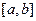
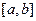
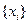
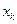
Рассмотрим некоторые из методов поиска. Предположим, что целевая функция на промежутке имеет один максимум. В этом случае, разбив узловыми точками , число которых , вычисляют целевую функцию в этих узловых точках. Предположим, что максимальное значение целевой функции будет в узле , тогда можно считать, что оптимальное решение находится на интервале . В результате произведено сужение отрезка, содержащего оптимальное решение. Полученный новый отрезок вновь разбивают на частей и т.д. При каждом разбиении отрезок, содержащий оптимальное решение уменьшаются в раз.

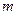
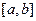
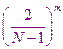
Предположим, что произведено шагов сужения. Тогда исходный отрезок уменьшается в раз.

То есть, делаем пока выполняется (*)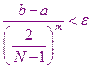

При этом производится вычислений целевой функции.

Требуется найти такое значение, чтобы выражение (*) было получено при наименьшем

числе вычислений .

Метод 37

Метод половинного деления.

Рассмотрим метод поиска при . Он называется методом половинного деления, так как на каждом шаге отрезок, содержащий оптимальное решение уменьшается в два раза.

Эффективность поиска можно повысить путём специального выбора точек, в которых вычисляется целевая функция на определённом шаге сужения.

Метод 38

Метод золотого сечения.

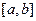
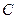
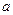
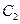
Одним из эффективных способов является метод золотого сечения. Золотым сечением отрезка называется точка для которой выполняется условие

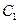
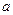
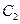
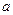
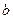
Таких точек две: =0,382 +0,618

=0,618 +0,382 .

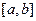
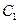
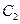
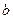
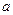
Отрезок делится точками и а после находится точка, целевая функция в которой максимальна. В результате чего находится изменённый отрезок длинною 0,618( — ) .

Одно значение золотого отрезка для суженного отрезка уже известно, поэтому на каждом последующем шаге требуется вычисление целевой функции только в одной точке (второй точки золотого сечения ).

Метод 39

Метод покоординатного подъёма (спуска).

Перейдём к рассмотрению задачи оптимизации в случае, когда целевая функция зависит от нескольких значений параметров. Простейшим методом поиска является метод покоординатного подъёма (спуска).

Задаётся исходная точка . Затем фиксируются все координаты, кроме первой, в результате получаем целевую функцию, зависящую от одного проектного параметра

.

Для этой функции находится максимальное значение и точка, в которой этот максимум достигается.

Затем фиксируем все координаты, кроме , и получаем целевую функцию, зависящую также только от одного параметра. . Затем находим таким же способом остальные значения, пока не найдём . Это будет означать окончание первого итерационного шага и получение точки . Затем мы повторяем процедуру, пока не достигнем заданной точности.

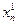
Метод 40

Метод градиентного подъёма (спуска).

Более эффективен метод градиентного подъёма (спуска).

Нужно выбрать начальную точку и вычисляют значение градиента целевой функции в этой точке. Градиент определяет направление наибыстрейшего возрастания целевой функции из точки . Затем делают небольшой шаг в этом направлении и приходят в точку . В этой точке процедуру повторяют и т.д.

Уравнение теплопроводности

Ранее (см. разд. 2.1.2, 2.1.3) уже были построены и исследованы разностные схемы решения смешанной задачи для одномерного уравнения теплопроводности:

(2.75)

Были получены две двухслойные схемы — явная (2.3) и неявная (2.4). В явной схеме значения сеточной функции на верхнем (j + 1)-ом слое вычисляли с помощью решения на нижнем слое [соотношение (2.13)]. Для нахождения решения на (j + 1)-м слое по неявной схеме была получена трехдиагональная система линейных алгебраических уравнений (2.22), которую решают методом прогонки.

Неявная схема безусловно устойчива, явная схема устойчива при выполнении условия

Обе схемы сходятся к решению исходной задачи со скоростью .

Схемы (2.3), (2.4) построены для случая, когда значения искомой функции (температуры) Uна границах х = 0, х = 1определяются заданными функциями . Однако граничные условия в смешанной задаче (2.75) могут быть и иными, в них может входить производная искомой функции. Например, если конец стержня х=0 теплоизолирован, то условие имеет вид

В этом случае, как и при решении волнового уравнения, данное условие нужно записывать в схемах (2.3), (2.4) в разностном виде.

Перейдем теперь к построению разностных схем для уравнения теплопроводности с двумя пространственными переменными. Примем для простоты а = 1. Тогда это уравнение можно записать в виде

(2.76)

Пусть при t=0 начальное условие задано в виде

(2.77)

В отличие от волнового уравнения, требующего два начальных условия, в уравнение теплопроводности входит только первая производная по t, и необходимо задавать одно начальное условие.

Часто задачи теплопроводности или диффузии, описываемые двумерным уравнением (2.76), решаются в ограниченной области. Тогда, кроме начального условия (2.77), нужно формулировать граничные условия. В частности, если расчетная область представляет прямоугольный параллелепипед (рис. 2.24), то нужно задавать граничные условия на его боковых гранях. Начальное условие (2.77) задано на нижнем основании параллелепипеда.

Рис. 2.24. Расчетная область

Введем простейшую сетку с ячейками в виде прямоугольных параллелепипедов, для чего проведем три семейства плоскостей: хi= ih1(i=0,1. I), (j=0,1. J), . Значение сеточной функции в узлах обозначим символом . С помощью этих значений можно построить разностные схемы для уравнения (2.76).

Рассмотренные выше схемы для одномерного уравнения легко обобщаются на двумерный случай.

Построим явную разностную схему, шаблон которой изображен на рис. 2.25. Аппроксимируя производные отношениями конечных разностей, получаем следующее сеточное уравнение:

Рис. 2.25. Шаблон двумерной схемы

Отсюда можно найти явное выражение для значения сеточной функции на (k + 1)-ом слое:

(2.78)

Условие устойчивости имеет вид

(2.79)

При получается особенно простой вид схемы (2.78):

(2.80)

Полученная схема сходится со скоростью

Формулы (2.78) или (2.80) представляют собой рекуррентные соотношения для последовательного вычисления сеточной функции во внутренних узлах слоев k = 1,2. К. На нулевом слое используется начальное условие (2.77), которое записывается в виде

(2.81)

Значения в граничных узлах вычисляют с помощью граничных условий.

Алгоритм решения смешанной задачи для двумерного уравнения теплопроводности изображен на рис. 2.26. Здесь решение хранится на двух слоях: нижнем (массив ) и верхнем (массив ). Блоки граничных условий необходимо сформировать в зависимости от конкретного вида этих условий. Результаты выводят на каждом слое, хотя можно ввести шаг выдачи (см. рис. 2.13).

Рис. 2.26. Алгоритм решения двумерного уравнения теплопроводности

Построим теперь абсолютно устойчивую неявную схему для решения уравнения (2.76), аналогичную схеме (2.4) для одномерного уравнения теплопроводности. Аппроксимируя в (2.76) вторые производные по пространственным переменным на (k + 1)-ом слое, получаем следующее разностное уравнение:

(2.82)

Это уравнение можно записать в виде системы линейных алгебраических уравнений относительно значений сеточной функции на каждом слое:

(2.83)

К этой системе уравнений нужно добавить граничные условия для определения значений сеточной функции в граничных узлах (т.е. при i= 0, I; j = 0, J). На нулевом слое решение находится из начального условия (2.77), представленного в виде (2.81).

Система (2.83), полученная для двумерного уравнения теплопроводности, имеет более сложный вид, чем аналогичная система (2.22) для одномерного случая, которую можно решить методом прогонки. Таким образом, распространение неявной схемы на многомерный случай приводит к значительному усложнению вычислительного алгоритма и увеличению объема вычислений.

Недостатком явной схемы (2.78) является жесткое ограничение на шаг по времени τ, вытекающее из условия (2.79). Существуют абсолютно устойчивые экономичные разностные схемы, позволяющие вести расчет со сравнительно большим значением шага по времени и требующие меньшего объема вычислений. Две из них будут рассмотрены в разд. 2.3.3.

Разностная аппроксимация начально-краевой задачи для уравнения теплопроводности. Понятие явной и неявной схемы.

Владислав Грузинский 5 лет назад Просмотров:

1 Разностная аппроксимация начально-краевой задачи для уравнения теплопроводности. Понятие явной и неявной схемы. 1 Разностная аппроксимация уравнения теплопроводности Рассмотрим различные варианты разностной аппроксимации линейного одномерного по пространству уравнения теплопроводности: где T > 0 некоторая константа. u t = u + fx, t, x 0, l, t 0, T ], 1.1 x Введем в области D = <0 x l, 0 t T >равномерную сетку с шагом по координате и шагом по времени: x =, = 0, 1. = l; t j = j, j = 0, 1. M, M = T. Уравнение 1.1 содержит как производные по пространственной переменной x, так и по времени t, поэтому для построения его разностной аппроксимации придется использовать узлы сетки, соответствующие различным j. Все узлы сетки, отвечающие фиксированному j, называют j-м временным слоем. Свойства разностных схем для уравнения 1.1 зависят от того, на каком слое j по времени аппроксимируется выражение u x. Рассмотрим возможные варианты. Вариант 1: явная схема. Для аппроксимации оператора L = t x приведенный на рис. 1. в уравнении 1.1 используем шаблон, 1

2 Рис. 1: Шаблон явной схемы для уравнения теплопроводности. Соответствующий разностный оператор L 0 u имеет вид: L 0 ux, t + ux, t ux +, t ux, t + ux, t u =. Далее для краткости будем использовать следующие стандартные обозначения: u = ux, t; û = ux, t +. Тогда: u t = û u, L 0 u = u t u xx. Найдем погрешность аппроксимации разностным оператором L 0 исходного дифференциального оператора L в точке x, t. В случае достаточно гладкой функции ux, t при достаточно малых шагах и имеем: u t = ux, t + ux, t = ux, t t + O, 1. Следовательно, разностный оператор L 0 аппроксимирует дифференциальный оператор L с погрешностью O + в точке x, t: L 0 u xx = ux, t x + O. 1.3 ux, t u = t ux, t x > << >L[ux,t] +O +. Введем сеточную функцию ϕ = ϕx, t j, аппроксимирующую правую часть fx, t уравнения 1.1 на всех внутренних узлах x, t j сетки с погрешностью O +. В качестве ϕ можно взять, например ϕx, t j = fx, t j. Тогда разностное уравнение L 0 y = ϕ будет аппроксимировать исходное дифференциальное уравнение теплопроводности 1.1 с первым порядком погрешности по и вторым по.

3 Вариант. Чисто неявная схема. Используем для аппроксимации оператора L = t x приведенный на рис.. в уравнении 1.1 шаблон, Рис. : Шаблон неявной схемы для уравнения теплопроводности. Тогда разностная аппроксимация оператора L уравнения теплопроводности будет выглядеть следующим образом: L 1 ux, t + ux, t ux +, t + ux, t + + ux, t + u = = u t û xx. Рассмотрим погрешность аппроксимации разностным оператором L 1 исходного дифференциального оператора L в точках x, t, x, t +. Так как для достаточно гладкой функции ux, t справедливы равенства û xx = ux, t + x + O = ux, t x + O +, 1.4 то с учетом 1. получаем, что оператор L 1 аппроксимирует дифференциальный оператор L в уравнении 1.1 с погрешностью O + в точках x, t и x, t + : L 1 ux, t u = t ux, t x > << >L[ux,t] +O + ux, t + = ux, t + +O +. > t << x >L[ux,t+] Беря в качестве сеточной аппроксимации правой части уравнения 1.1, например, функцию ϕx, t j = fx, t j+1, получим разностное уравнение L 1 y = ϕ, аппроксимирующее 1.1 с погрешностью O +. 3

4 Вариант 3. Неявная схема с весами. Используем шаблон, приведенный на рис. 3, и линейную комбинацию операторов L 0 и L 1 для аппроксимации дифференциального оператора L: L σ u = σl1 u+1 σl0 u = σu t σû xx +1 σu t 1 σu xx = u t σû xx + 1 σu xx, где σ 0, 1. Рис. 3: Шаблон неявной схемы с весами для уравнения теплопроводности. Пользуясь равенствами 1., 1.3 и 1.4, получаем, что оператор L σ аппроксимирует исходный дифференциальный оператор L с погрешностью O + в точках x, t, x, t+ при любом σ. По определению погрешность ψx, t = L σ u Lu 1.5 аппроксимации выражения Lu разностным выражением L σ u может вычисляться в любой точке x, t, а не обязательно в каком-либо узле сетки, так как в соотношении 1.5 функция ux, t это произвольная достаточно гладкая функция непрерывных аргументов x и t. Поэтому рассмотрим погрешность аппроксимации оператором L σ дифференциального оператора L в центральной точке x, t шаблона, приведенного на рис. 3. Пользуясь для достаточно гладкой функции ux, t разложением в ряд Тейлора в окрестности точки x, t + 0.5, при малых и получаем: ux, t + ux, t u t = = u t + O, x,t+0.5 û xx = u x + O = u x,t+ x + 3 u x,t+0.5 t x + O +, x,t+0.5 u xx = u x + O = u x,t x x,t u t x + O +. x,t+0.5 4

5 Следовательно, при σ = 0.5 в точке x, t оператор L 0.5 в силу своей симметрии аппроксимирует L со вторым порядком погрешности аппроксимации по и : L σ u = ux, t + t ux, t + x > << >L[ux,t+ ] 3 ux, t + σ 1 + O +. > <<>x t 0 при σ=0.5 Для того, чтобы получить разностное уравнение, аппроксимирующее дифференциальное уравнение u t = u + fx, t x с погрешностью O + в точке x, t +, достаточно взять в качестве сеточной аппроксимации правой части fx, t этого уравнения функцию ϕx, t j = fx, t j Итак, разностное уравнение L 0.5 y = ϕ, где ϕx, t j = fx, t j + 0.5, аппроксимирует уравнение 1.1 со вторым порядком погрешности по и. Реализация явной, неявной и симметричной разностных схем для начально-краевой задачи для уравнения теплопроводности на отрезке. Пример.1. Постройте явную разностную схему для следующей начально-краевой задачи на отрезке x [0, 1]: u t = u + x, 0 6 задаче с однородными граничными условиями: v t = v, 0 7 Итак, первый вариант явной разностной схемы для задачи.1, обладающей погрешностью аппроксимации O +, имеет вид: y j = yj 1 yj + yj +1 + x, = 1. 1, j = 0, 1. M 1, y 0 3πx = sn, = 0, 1. 4 y j 0 = 0, y j yj 1 = t j, j = 0, 1. M. Рассмотрим алгоритм решения системы.4. При j = 0 значения y j известны из начального условия. Следовательно, при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Найти их можно следующим образом: 1 при = 1. 1 из первого уравнения системы.4 находим = y j + y j +1 yj + yj 1 + x ; при = 0 и = пользуемся граничными условиями, учитывая, что 1 и 1 уже известны: 0 = 0, = yj t j+1; 3 переходим на новый слой по времени, увеличивая j на единицу и повторяем действия 1 и. На рис.4-6 приведены результаты решения системы.4 для = 50 и M = Рис. 4: Аналитическое решение задачи.1. Если мы хотим, чтобы явная схема аппроксимировала исходную задачу с погрешностью O +, то можно использовать тот же прием, который применялся ранее для ап- 7

8 Рис. 5: Численное решение задачи.1 с помощью явной схемы. Рис. 6: Погрешность численного решения задачи.1 с помощью явной схемы. проксимации граничного условия, содержащего производную, в краевой задаче для обыкновенного дифференциального уравнения на отрезке. Пусть ux, t решение задачи.1. Рассмотрим выражение: u x = ux, t ux, t ux, t = ux, t + O = x x ux, t = ux, t x + O. x t Заменяя в нем производную u t конечной разностью: ux, t t = ux, t ux, t + O, 8

9 получим ux, t ux, t = ux, t x ux, t ux, t x + O +. Переходя в полученном равенстве к пределу при x 1 и учитывая, что по условию u x = t, x=1 находим, что при t = t j+1 имеет место равенство: u j+1 uj+1 1 = t j+1 u j+1 uj 1 + O +. Следовательно, разностное уравнение yj+1 1 = t j+1 yj 1.5 аппроксимирует граничное условие Неймана при x = 1 с погрешностью O +. Таким образом, меняя в схеме.4 уравнение.3 на.5, мы получим схему, аппроксимирующую исходную задачу на ее решении с погрешностью O +. Уравнение.5 удобно переписать в виде: 1 = t j yj, j = 0, 1. M 1, и использовать при уже найденных 1, yj для завершения перехода на слой j + 1. Результаты расчетов по соответствующей явной схеме на той же сетке, что и в предыдущем случае, приведены на рис Рис. 7: Численное решение задачи с помощью явной схемы с граничным условием.5. 9

10 Рис. 8: Погрешность решения задачи с помощью явной схемы с граничным условием.5. Также для получения схемы, имеющей погрешность аппроксимации O +, можно аппроксимировать граничное условие Неймана при x = 1 с помощью трехточечной первой разностной производной: 3 4yj yj+1 Переписывая это уравнение в виде = t j+1, j = 0, 1. M 1. = 4 3 yj yj+1 + t j+1 3,.6 мы можем использовать его для завершения перехода на слой j + 1 при уже найденных 1 и yj+1. Погрешность вычислений по схеме с условием.6 приведена на рис. 9. Рис. 9: Погрешность решения задачи с помощью явной схемы с граничным условием.6. 10

11 Пример.. Постройте чисто неявную разностную схему для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Используем ту же сетку, что и в предыдущем примере с той лишь разницей, что соотношение шагов и теперь может быть любым. Разностная аппроксимация уравнения в соответствии с неявной схемой имеет вид: y j = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1..7 Дополним разностное уравнение.7 начальными и граничными условиями на сетке. Как и в случае явной схемы, начальное условие и граничное условие Дирихле при x = 0 аппроксимируются точно: y 0 3πx = sn, = 0, 1. ; 0 = 0, j = 1. M 1. Для аппроксимации граничного условия при x = 1 используем те же три способа, что и в случае явной схемы, разобранной в предыдущем примере. Первый вариант аппроксимации граничного условия Неймана при x = 1: yj+1 1 = t j+1, j = 1. M 1. Получающаяся при этом неявная разностная схема: y 0 3πx = sn, = 0, 1. 0 = 0, j = 0, 1. M 1, y j yj+1 1 = yj+1 1 yj x, = 1. 1, j = 0, 1. M 1, = t j+1, j = 0, 1. M 1.8 имеет погрешность аппроксимации O +. Значения сеточной функции y j на нулевом слое по времени известны из начального условия, поэтому при каждом фиксированном j = 0, 1. M 1 неизвестными являются. Система уравнений, которым они удовлетворяют, имеет вид: 0 = 0, yj = yj t j+1, + yj+1 +1 = y j + x, = 1. 1,.9 11

12 то есть является системой с трехдиагональной матрицей: 0 = κ µ 1, A 1 C + B +1 = F, = 1. 1, = κ 1 + µ,.10 где κ 1 = 0, µ 1 = 0, A = B =, C = 1 +, F = y j + x, κ = 1, µ = t j+1. Очевидно, что достаточные условия устойчивости прогонки: A > 0, B > 0, C A + B, C A + B, = 1. 1, 0 κ p 1, p = 1, для системы.9 выполнены. Решая систему.9 методом прогонки и последовательно увеличивая значения j на единицу, мы полностью решим систему.8. Результаты вычислений по неявной схеме.8 в случае = M = 50 приведены на рис Рис. 10: Численное решение задачи.1 с помощью неявной схемы.8. Рис. 11: Погрешность численного решения задачи.1 с помощью неявной схемы.8. 1

13 Второй вариант аппроксимации граничного условия Неймана при x = 1: 1 = t j yj, j = 0, 1. M В этом случае для неизвестных при каждом фиксированном j получаем трехдиагональную систему вида.10, где κ = 1 1 +, µ = κ t j yj Погрешность расчетов по соответствующей неявной схеме в случае = M = 50 приведена на рис. 1.. Рис. 1: Погрешность решения задачи.1 с помощью неявной схемы с граничным условием.11. Третий вариант аппроксимации граничного условия Неймана при x = 1: = 4 3 yj yj+1 + t j+1 3 Для того, чтобы получить для неизвестных.1 систему с трехдиагональной матрицей при каждом фиксированном j, исключим из уравнения.1 неизвестное. Для этого воспользуемся уравнением.7 при = 1: yj yj yj+1 = F 1. Следовательно, = + 1 yj+1 F 1, 13

14 и уравнение.1 принимает вид: = 1 В результате для неизвестных.10, где κ = 1, 1 + F 1 + t j+1. приходим к системе с трехдиагональной матрицей вида µ = F 1 + t j+1. Погрешность расчетов по соответствующей схеме в случае = M = 50 приведена на рис. 13. Рис. 13: Погрешность численного решения задачи.1 с помощью неявной схемы с граничным условием.1. Пример.3. Постройте симметричную разностную схему схему с весом σ = 0.5 для начально-краевой задачи.1. Сравните численное решение с аналитическим и исследуйте зависимость погрешности от шагов сетки. Решение. Аппроксимация уравнения u t = u x + x в соответствии с симметричной разностной схемой имеет вид: y j = 1 y j+1 1 yj yj 1 yj + yj +1 + x,.13 где = 1. 1, j = 0, 1. M 1. Разностное уравнение.13 аппроксимирует исходное дифференциальное уравнение теплопроводности с погрешностью O + на всех внутренних узлах сетки. 14

15 Начальное условие и условие Дирихле при x = 0 аппроксимируются так же, как и в двух рассмотренных ранее случаях. Граничное условие Неймана при x = 1 можно аппроксимировать как с первым, так и со вторым порядком по. Если в качестве аппроксимации условия при x = 1 берется разностное уравнение yj+1 1 = t j+1, j = 1. M 1, то схема будет иметь погрешность аппроксимации O +. Соответствующая система для неизвестных будет трехдиагональной: 0 = 0, A 1 C + B +1 = F, = 1. 1, = yj t j+1,.14 где A = B =, C = 1 + A, F = y j + x + yj 1 yj + yj +1. Достаточные условия устойчивости прогонки для системы.14 выполнены. Погрешность решения задачи по схеме.14 для = M = 50 приведена на рис. 14. Рис. 14: Погрешность численного решения задачи.1 с помощью симметричной схемы. Построим аппроксимацию граничного условия Неймана при x = 1 с погрешностью O +. Рассмотрим равенство: ux, t ux, t = ux, t x ux, t t x + O,.15 где ux, t решение исходной задачи.1. Положим в равенстве.15 t = t j Так как ux, t j ux, t j =

16 и получаем: 1 = 1 u j uj 1 + uj+1 ux, tj ux, t j ux, t t t=tj +0.5 u j+1 1 = ux, t x + ux, t j+1 ux, t j+1 + O = ux, t j+1 ux, t j x,t j O, u j+1 u j x + O +. Перейдем в полученном равенстве к пределу при x 1 то есть при, учитывая граничные условия задачи: 1 u j uj 1 + uj+1 uj = t j Следовательно, разностное уравнение y j yj 1 + yj+1 yj+1 1 = t j +0.5 будет аппроксимировать условие u x = t x=1 yj u j+1 uj с погрешностью O +. Соответствующая система для вид: где 0 = 0, 1 1 A 1 C + B +1 = F, = 1. 1, = κ 1 + µ, 1 κ = 1 +, µ = κ 1 + yj + O +., j = 0, 1. M 1.16 при фиксированном j имеет + t j + y j + yj Погрешность, получаемая при численном решении задачи с использованием граничного условия.16, для = M = 50 приведена на рис. 15. Такой же порядок погрешности аппроксимации можно получить, используя граничное условие = 4 3 yj yj+1 + t j Исключим из этого уравнения неизвестное, используя уравнение.13 при = 1: Так как yj yj+1 = F 1. = + 1 yj+1 F 1, 16

17 Рис. 15: Погрешность численного решения задачи.1 с помощью симметричной схемы с граничным условием.16. уравнение.18 можно переписать в виде: = F 1 + t j+1. В результате мы снова придем к системе с трехдиагональной матрицей вида.17 для неизвестных при каждом фиксированном j = 0, 1. M 1, где теперь κ = 1, µ = F 1 + t j+1. Погрешность решения по предложенной схеме при = M = 50 приведена на рис. 16. Рис. 16: Погрешность решения задачи с помощью симметричной схемы с граничным условием

18 3 Задачи для самостоятельного решения Решите аналитически и численно при помощи явной, неявной и симметричной схем начальнокраевую задачу для уравнения теплопроводности на отрезке: u t = u a + fx, t, x 0, l, t 0, T ], x ux, 0 = u 0 x, u γ 0 x + δ 0u = g 0 t, x=0 u γ 1 x + δ 1u = g 1 t, x=l где: x а a =, f = cos e t, u 0 = π x, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 0, l = π; б a = 1, f = e t x / 1, u 0 = 1 + e t x /, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 0, g 1 = e t, l = 1; в a = 0.5, f = e t, u 0 = 1 + sn 3x, γ 0 = 0, δ 0 = 1, γ 1 = 1, δ 1 = 0, g 0 = e t, g 1 = 0, l = π/; 3πx г a = 1, f = 0, u 0 = 3 x + cos, γ 0 = 1, δ 0 = 0, γ 1 = 0, δ 1 = 1, g 0 = 1, g 1 = 1, l = ; 4 д a = 0.1, f = 0, u 0 = cosπx + x + x, γ 0 = 1, δ 0 = 0, γ 1 = 1, δ 1 = 0, g 0 = 1, g 1 = 5, l =. Сравните результаты численного решения по разным схемам между собой и с аналитическим решением задачи. 18