Явная схема уравнения теплопроводности онлайн

Решение уравнения теплопроводности

Дата добавления: 2013-12-23 ; просмотров: 3588 ; Нарушение авторских прав

Решение алгебраических уравнений методом Ньютона

Достаточно популярным методом решения уравнений является метод касательных, или метод Ньютона. В этом случае уравнение вида f(x) = 0 решается следующим образом. Сначала выбирается нулевое приближение (точка x₀). В этой точке строится касательная к графику y = f(x). Точка пересечения этой касательной с осью абсцисс является следующим приближением для корня (точка x₁). В этой точке снова строится касательная и т.д. Последовательность точек x₀, x₁, x₂… должна привести к истинному значению корня. Условием сходимости является .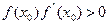

Так как уравнение прямой, проходящей через точку x₀, f(x₀) (а это и есть касательная), записывается в виде

а в качестве следующего приближения x₁ для корня исходного уравнения принимается точка пересечения этой прямой с осью абсцисс, то следует положить в этой точке y = 0:

,

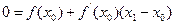
откуда немедленно следует уравнение для нахождения следующего приближения через предыдущее:

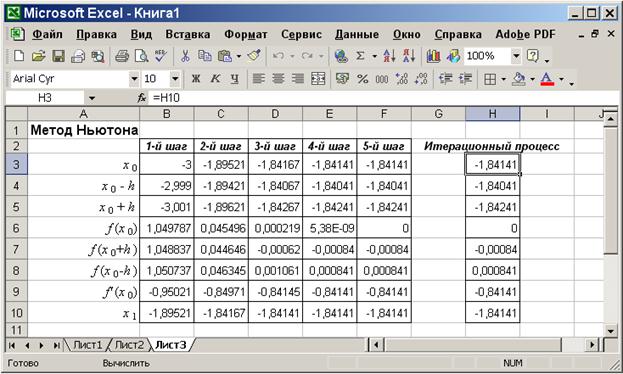
На Рис. 3 показана реализация метода Ньютона средствами Excel. В ячейку B3 вводится начальное приближение (x₀ = -3), а затем остальных ячейках столбца вычисляются все промежуточные величины вплоть до вычисления x₁. Для выполнения второго шага в ячейку C3 вводится значение из ячейки B10 и процесс вычислений повторяется в столбце C. Затем, выделив ячейки C2:C10 можно, потянув за маркер в правом нижнем углу выделенной области, распространить его на столбцы D:F. В итоге в ячейке F6 получено значение 0, т.е. значение в ячейке F3 есть корень уравнения.

Этот же результат можно получить, используя циклические вычисления. Тогда после заполнения первого столбца и получения первого значения x₁ следует ввести в ячейку H3 формулу =H10. При этом вычислительный процесс будет зациклен и для того, чтобы он выполнялся, в меню Сервис | Параметры на вкладке Вычисления необходимо установить флажок Итерации и указать предельное число шагов итерационного процесса и относительную погрешность (установленное по умолчанию число 0,001 явно недостаточно во многих случаях), по достижении которой вычислительный процесс остановится.

Как известно, такие физические процессы, как перенос тепла, перенос массы в процессе диффузии, подчиняются закону Фика

,

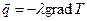
где l — коэффициент теплопроводности (диффузии), а T – температура (концентрация), а 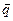– поток соответствующей величины. Из математики известно, что дивергенция потока равна объемной плотности источника Q этой величины, т.е.

или, для двухмерного случая, когда исследуется распределение температуры в одной плоскости, это уравнение может быть записано в виде:

(4)

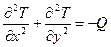
Решение этого уравнения аналитически возможно только для областей простой формы: прямоугольник, круг, кольцо. В остальных ситуациях точное решение этого уравнения невозможно, т.е. невозможно и определить распределение температуры (или концентрации вещества) в сложных случаях. Тогда приходится использовать приближенные методы решения таких уравнений.

Приближенное решение уравнения (4) в области сложной формы состоит из нескольких этапов: 1) построение сетки; 2) построение разностной схемы; 3) решение системы алгебраических уравнений. Рассмотрим последовательно каждый из этапов и их реализацию с помощью пакета Excel.

Построение сетки. Пусть область имеет форму, показанную на рис. 4. При такой форме точное аналитическое решение уравнения (4), например, методом разделения переменных, невозможно. Поэтому будем искать приближенное решение этого уравнения в отдельных точках. Нанесем на область равномерную сетку, состоящую из квадратов со стороной h. Теперь, вместо того, чтобы искать непрерывное решение уравнения (4), определенное в каждой точке области, будем искать приближенное решение, определенное только в узловых точках сетки, нанесенной на область, т.е. в углах квадратов.

Построение разностной схемы.Для построения разностной схемы рассмотрим произвольный внутренний узел сетки Ц (центральный) (рис.5). С ним соседствуют четыре узла: В (верхний), Н (нижний), Л (левый) и П (правый). Напомним, расстояние между узлами в сетке равно h. Тогда, используя выражение (2) для приближенной записи вторых производных в уравнении (4), можно приближенно записать:

,

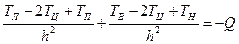
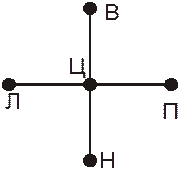
откуда легко получить выражение, связывающее значение температуры в центральной точке с ее значениями в соседних точках:

(5)

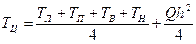
Выражение (5) позволяет нам, зная значения температуры в соседних точках, вычислить ее значение в центральной точке. Такая схема, в которой производные заменяются конечными разностями, а для поиска значений в точке сетки используются только значения в ближайших соседних точках, называется цетрально-разностной схемой, а сам метод – методом конечных разностей.

Нужно понимать, что уравнение, аналогичное (5), мы получаем ДЛЯ КАЖДОЙ точки сетки, которые, таким образом, оказываются связанными друг с другом. То есть мы имеем систему алгебраических уравнений, в которой число уравнений равно числу узлов сетки. Решать такую систему уравнений можно различными методами.

Решение системы алгебраических уравнений. Метод итераций. Пусть в граничных узлах температура задана и равна 20, а мощность теплового источника равна 100. Размеры нашей области заданы и равны по вертикали 6, а по горизонтали 8, так что сторона квадрата сетки (шаг) h = 1. Тогда выражение (5) для вычисления температуры во внутренних точках принимает вид

(6)

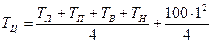
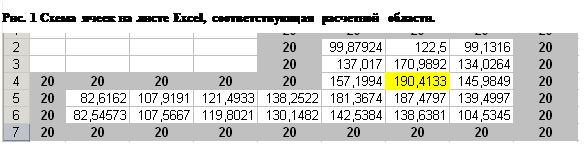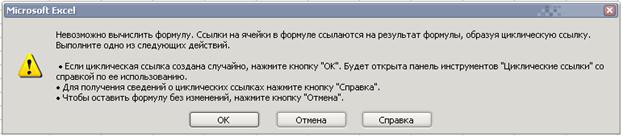
Поставим в соответствие каждому УЗЛУ ячейку на листе Excel. В ячейках, соответствующих граничным точкам, введем число 20 (на рис. 6 они выделены серым цветом). В остальных ячейках запишем формулу (6). Например в ячейке F2 она будет выглядеть следующим образом: =(F1 + F3 + E2 + G2)/4 + 100*(1^2)/4. Записав эту формулу в ячейку F2, можно ее скопировать и вставить в остальные ячейки области, соответствующие внутренним узлам. При этом Excel будет сообщать о невозможности проведения вычислений из-за зацикливания результатов:

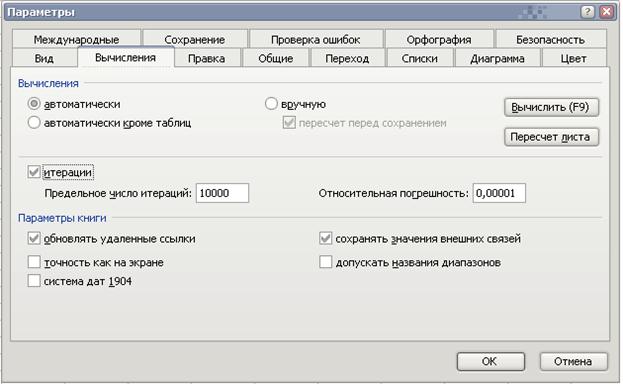
Нажмите «Отмена» и перейдите в окно Сервис|Параметры|Вычисления, где установите флажок в разделе «Итерации», указав при этом в качестве относительной погрешности величину 0,00001, а в качестве предельного количества итераций 10000:

Такие значения обеспечат нам малую СЧЁТНУЮ погрешность и гарантируют, что итерационный процесс дойдет до заданной погрешности.

Однако эти значения НЕ ОБЕСПЕЧИВАЮТ малую погрешность самого метода, так как последняя зависит от погрешности при замене вторых производных конечными разностями. Очевидно, что эта погрешность тем меньше, чем меньше шаг сетки, т.е. размер квадрата, на котором строится наша разностная схема. Это означает, что точно ВЫЧИСЛЕННОЕ значение температуры в узлах сетки, представленное на рис. 6, на самом деле может оказаться совсем не соответствующим действительности. Существует единственный метод проверить найденное решение: найти его на более мелкой сетке и сравнить с предыдущим. Если эти решения отличаются мало, то можно считать, что найденное распределение температуры соответствует действительности.

Уменьшим шаг вдвое. Вместо 1 он станет равным ½. Число узлов у нас соответственно изменится. По вертикали вместо 7 узлов (было 6 шагов, т.е. 7 узлов) станет 13 (12 квадратов, т.е. 13 узлов), а по горизонтали вместо 9 станет 17. При этом не следует забывать, что величина шага уменьшилась вдвое и теперь в формуле (6) вместо 1 2 нужно в правой части подставлять (1/2) 2 . В качестве контрольной точки, в которой будем сравнивать найденные решения, возьмем точку с максимальной температурой, отмеченную на рис. 6 желтым цветом. Результат вычислений показан на рис. 9:

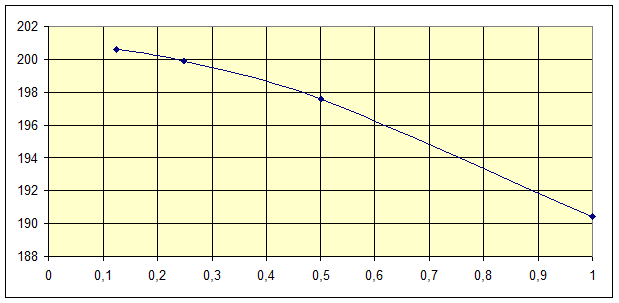
Видно, что уменьшение шага привело к существенному изменению значения температуры в контрольной точки: на 4%. Для повышения точности найденного решения следует ещё уменьшить шаг сетки. Для h = ¼ получим в контрольной точке 199,9, а для h = 1/8 соответствующее значение равно 200,6. Можно построить график зависимости найденной величины от величины шага:

Из рисунка можно сделать вывод, что дальнейшее уменьшение шага не приведет к существенному изменению температуры в контрольной точке и точность найденного решения можно считать удовлетворительной.

Используя возможности пакета Excel, можно построить поверхность температуры, наглядно представляющую ее распределение в исследуемой области:

Уравнение теплопроводности в tensorflow

Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:

Линейная начально-краевая задача для двумерного уравнения теплопроводности:

Хотя правильнее было бы назвать это уравнением диффузии.

Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.

Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.

Численный алгоритм

Разностная схема:

Чтобы проще было расписывать, введем операторы:

Явная разностная схема:

В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.

Неявная разностная схема:

Перенесем в левую сторону все связанное с , а в правую и домножим на :

По сути мы получили операторное уравнение над сеткой:

что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:

Заменив на нашу оценку , запишем функционал ошибки:

где — ошибка в узлах сетки.

Будем итерационно минимизировать функционал ошибки, используя градиент.

В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.

Реализация на tensorflow

Кратко о tensorflow

В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.

tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).

Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.

По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.

Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.

Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.

Запуск:

Результаты

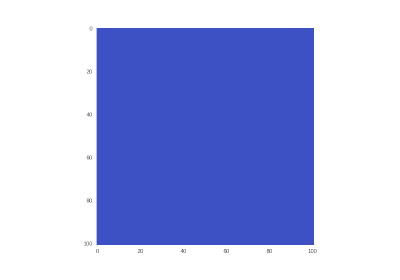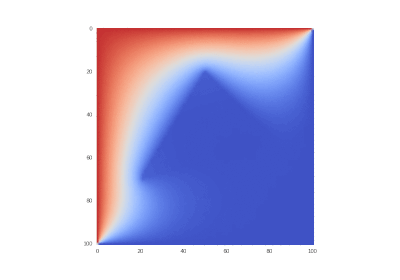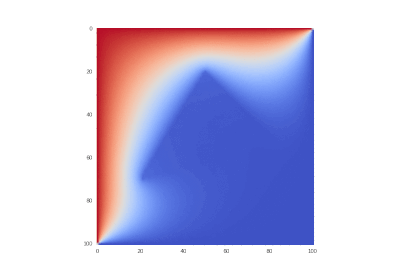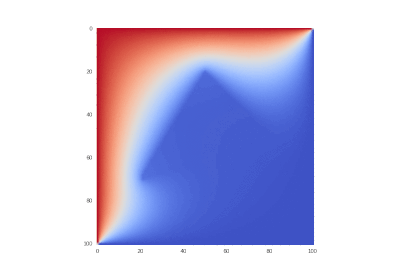
Условие как и оригинальное, но без в уравнении:

Что легко правится в коде:

Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.

Условие с одним нагревающимся краем:

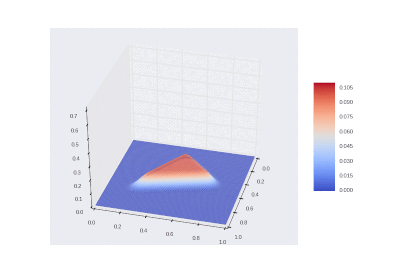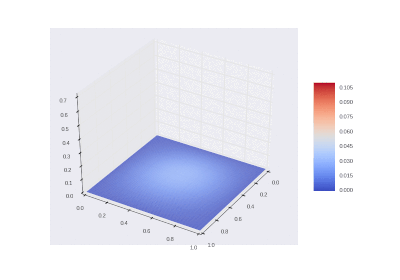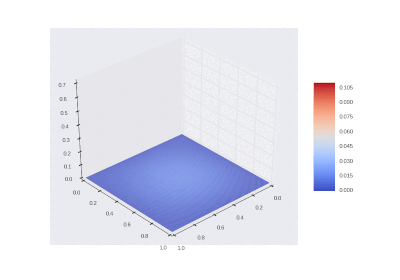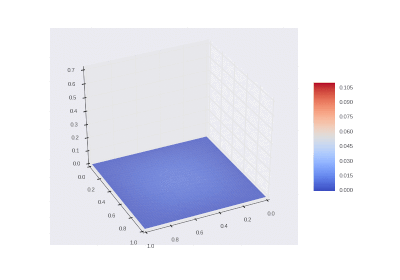
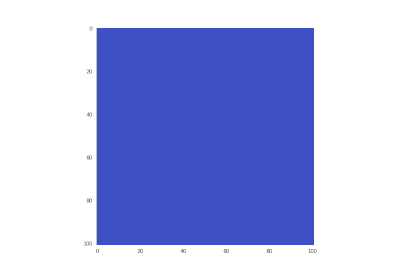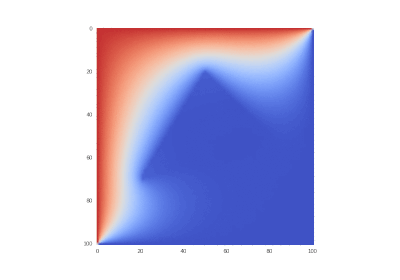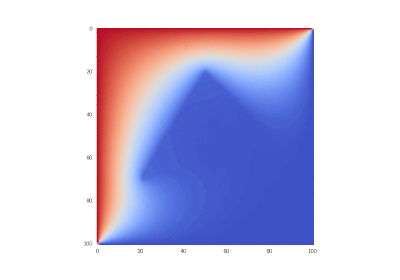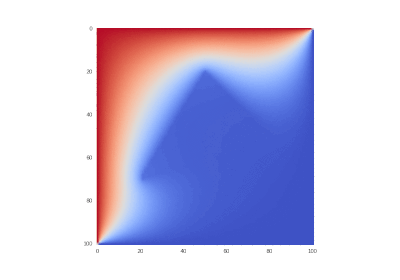
Условие с остыванием изначально нагретой области:

Условие с включением нагрева в области:

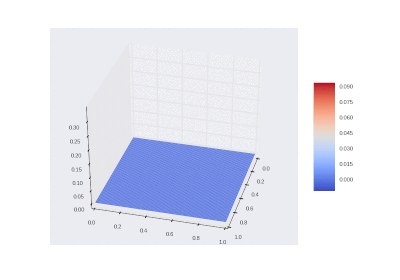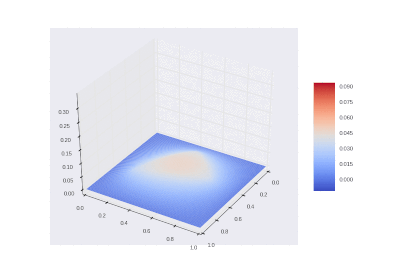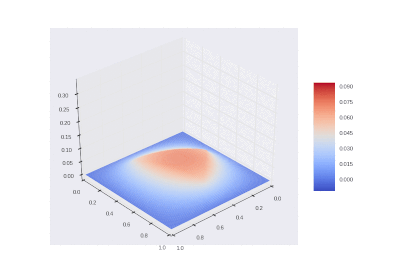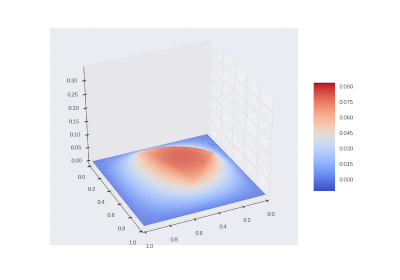
Рисование гифок

Функция рисования 3D-гифки:

В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame

Функция рисования 2D-гифки:

Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.

• Intel Core i7 6700HQ 2600 МГц,
• NVIDIA GeForce GTX 960M.

Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:

Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.

Лабораторная работа №7

Решение уравнений в частных производных методом сеток.

Решить одномерное уравнение теплопроводности методом сеток.

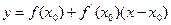
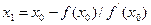
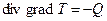
Используя явную схему метода сеток, проинтегрировать одномерное уравнение теплопроводности со следующими начальными и граничными условиями: , , , , .

Наиболее простой конечно-разностной схемой, применяемой для численного решения уравнений с частными производными, является явная схема. В случае одномерного уравнения теплопроводности она записывается следующим образом:

, j = 1, . , n , ( 10 )

где , n — число узлов cетки по x. ( 11 )

1. В первой строке введем названия параметров: n , l , c , Dx, g, m, Dt, a, b, а под ними в соответствующих ячейках — числовые значения (n=10, l=1, c=1). Для Dx вводим соответствующую формулу =B2/A2 (Dx=l/n). Исходя из условий устойчивости явной схемы, выбираем m=0,5 и выражаем Dt через m из уравнения ( 11 ) (=$D$2*$D$2*0,5).Для параметров функций, задающих краевые и начальные условия, выбираем следующие значения: g=8, a=10000, b=250.

2. В столбце А, как мы уже делали в предыдущих работах, разместим вычисление значений x, соответствующих узлам сетки. В третьей строке разместим формулы, вычисляющие значения узлов по времени. В столбце Вразместим формулы, вычисляющие начальное распределение температуры по длине стержня =EXP($E$2*A4-$E$2*A4*A4), а в четвертой и четырнадцатой строках, начиная со столбца С, -формулы, вычисляющие значения температуры на концах стержня: =EXP(-$H$2*C$3*C$3+$I$2*C$3).

3. В ячейку С5вводим формулу, реализующую конечно-разностное уравнение ( 10 ) —=B5+$F$2*(B6-2*B5+B4). Распространяем эту формулу на всю область, ограниченную краевыми и начальными условиями.

4. Результирующая таблица и построенная с использованием данных из блока A3:J14 диаграмма представлены на рис. 24 и 25.

Рис. 24. Решение одномерного уравнения теплопроводности с использованием явной схемы метода сеток.

Рис. 25. Графическое изображение решения одномерного уравнения теплопроводности.

Литература

1. Фигурнов В. Э. IBM PC для пользователя. 6-е изд. — М.: ИНФРА-М, 1995.

2. Шиб Й. Windows 3.1 (русская версия ) : Пер. с нем. — М. : БИНОМ, 1995.

3. Николь Н., Альбрехт Р. Электронные таблицы Excel 5.0: Практ. пособ. / Пер. с нем. — М.: ЭКОМ.,1995.

4. Наймершайм Дж. Excel 5.0 for Windows: Учебное пособие / Пер. с англ. — М.: Междунар. отношения, 1995.

5. Осейко Н. Н. Excel 5.0 для пользователя: — К.: Торгово — издательское бюро ВНV, 1994.

6. Альтхаус М. Excel. Секреты и советы / Пер. с нем. М.: БИНОМ, 1995.

7. Основы работы с Excel 5.0 : Методические указания / ИГХТА. — Иваново, 1996.

8. Численные методы : Методические указания / ИХТИ. — Иваново, 1988.

9. Методические указания и задания к практическим занятиям по вычислительной математике : Методические указания / ИХТИ. — Иваново, 1988.

10. Моделирование сложных изотермических реакций, описываемых линейными дифференциальными уравнениями : Методические указания / ИХТИ. — Иваново, 1992.

Оглавление

Лабораторная работа № 1. Основные элементы работы в EXCEL . . . 3

Лабораторная работа № 2. Построение графиков и диаграмм . . . . . . 7

Лабораторная работа № 3. Вычисление определенных интегралов . . 15

Лабораторная работа № 4. Решение систем линейных уравнений . . . 17

Лабораторная работа № 5. Обработка экспериментальных данных . 20

Лабораторная работа № 6. Решение обыкновенных дифференциаль-

ных уравнений и систем обыкновенных дифференциальных уравне-

Лабораторная работа № 7. Решение уравнений в частных производ-

ных методом сеток . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

Дата добавления: 2015-02-09 ; просмотров: 18 ; Нарушение авторских прав