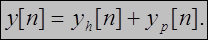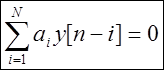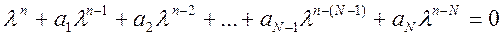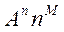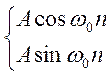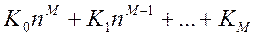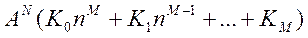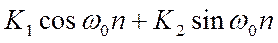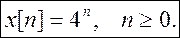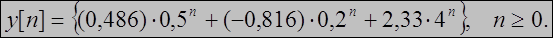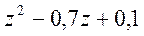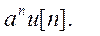РАЗНОСТНЫЕ УРАВНЕНИЯ. Z-ПРЕОБРАЗОВАНИЕ И ЕГО ПРИМЕНЕНИЯ
- Мария Мосальская 5 лет назад Просмотров:
1 Министерство образования ресублики Беларусь Учреждение образования «Могилевский государственный университет родовольствия» РАЗНОСТНЫЕ УРАВНЕНИЯ Z-ПРЕОБРАЗОВАНИЕ И ЕГО ПРИМЕНЕНИЯ Учебно-методическое особие для обесечения уравляемой самостоятельной работы студентов сециальности Автоматизация технологических роцессов и роизводств Могилѐв 014
2 УДК ББК 1611 Г 65 Рецензенты: дф-мн, зав кафедры высшей математики УО МГУП АМ Гальмак, ктн, доцент кафедры АТПП УО МГУП ЕЛ Волынская Рекомендовано кафедрой высшей математики УО МГУП, научнометодическим советом УО МГУП Составители: СВ Подолян ИВ Юрченко Разностные уравнения Z-реобразование и его рименения: учебнометодическое особие / сост СВ Подолян, ИВ Юрченко Могилев: МГУП, с ISBN В учебно-методическом особии изложены теоретические сведения о теме «Разностные уравнения Z-реобразование и его рименения» учебной рограммы о дисцилине «Высшая математика» для студентов сециальности Автоматизация технологических роцессов и роизводств Приведены римеры, иллюстрирующие основные методы решения разностных уравнений и осуществления рямого и обратного Z-реобразования Рассмотрено рименение Z-реобразования к анализу выходных роцессов линейных дискретных стационарных динамических систем Включены рактические задания для самостоятельного выолнения и ответы к ним Пособие редназначается для студентов сециальности в качестве методического обесечения УСРС УДК ББК 1611 ISBN Учреждение образования «Могилевский государственный университет родовольствия», 014
3 1 Решетчатые функции Содержание 11 Понятие решетчатой функции 4 1 Конечные разности решетчатых функций 5 13 Разностные уравнения 6 14 Решение линейных однородных разностных уравнений 7 Z-реобразование 1 Понятие о Z-реобразовании 10 Основные свойства Z-реобразования 1 3 Нахождение оригинала о изображению 1 3 Применения Z-реобразования 31 Решение линейных разностных уравнений с остоянными коэффициентами и их систем 15 3 Применение Z-реобразования к анализу выходных роцессов линейных дискретных стационарных динамических систем 18 Задачи для самостоятельного решения 1 Сисок литературы Приложения 3 3
4 1 Решетчатые функции 11 Понятие решетчатой функции Рассмотрим функцию f(t), которая оределена в отдельных изолированных точках (дискретных) t 1, t,, t, некоторого ромежутка Т Следует обратить внимание, что еременная величина t не является нерерывно изменяющейся на ромежутке Т, а ринимает на нем только отдельные изолированные значения Наример, функция f(t) = t 3, где еременная величина t ринимает на ромежутке [ ; ] значения: t = ; 1,5; 1; 0; 1; 1,5; Изобразим на рисунке 11 график этой функции (значения функции отметим точками) Рисунок 11 График функции f(t) Для дальнейшего рассмотрения обозначим f(t ) = f, где f оследовательность чисел, значений функции f(t) ри t = t 1, t,, t, t + 1, ; t + 1 > t Функции f(t ), у которых аргумент t является целым числом, t Z, целесообразно обозначить через f() Такие функции называются решетчатыми функциями Предлагается самостоятельно остроить графики следующих решетчатых функций: а) f() = С = const, Z; б) f() =, Z; с) f() = ln, N 4
5 1 Конечные разности решетчатых функций Пусть дана решетчатая функция f(), = 0, 1,, Функция f() = f( + 1) f() (11) называется конечной разностью ервого орядка или ервой (конечной) разностью Функция f() = ( f()) называется конечной разностью второго орядка или второй (конечной) разностью Вторая (конечная) разность оределяется следующим выражением: f() = f( + 1) f() = f( + ) f( + 1) (f( + 1) f()) = = f( + ) f( + 1) + f() (1) Рекуррентно -я (конечная) разность оределяется следующим образом: k f() = k 1 f( + 1) k 1 f() = f( + k) C k 1 f( + k 1) + C k f( + k ) + ( 1) i C k i f( + k i) + + ( 1) k f(), (13) где C k i = k! i!( k i)! биномиальные коэффициенты, 0 f() = f() Формулы (11) (13) выражают разности решетчатой функции через значения этой функции в целочисленных точках Рассмотрим, как можно выразить значения самой решетчатой функции f() через ее разности различных орядков откуда Из (11) олучим f( + 1) = f() + f() На основе олученного равенства и равенства (1) находим По индукции находим f() = f( + ) f() f(), f( + ) = f() + f() + f() f( + k) = f() + C k 1 f() + C k f() + + k f() (14) Если оложить в (14) = 0,олучим f(k) = f(0) + C k 1 f(0) + C k f(0) + + k f(0) (15) Формулы (14), (15) оределяют значения решетчатой функции через ее конечные разности до орядка k включительно и редставляют собой дискретный аналог формул Тейлора для нерерывной функции Пример 11 Вычислить разности k f(), = 1. если f() = е Решение Последовательно находим: 5
6 f() = е ( +1) е = е (е 1); f() = е ( + 1) (е 1) е (е 1) = (е 1) е (е 1) = е (е 1) По индукции находим k f() = е (е 1) k, k = 1,, 13 Разностные уравнения 131 Основные онятия о разностных уравнениях Разностным уравнением k-го орядка называют любое соотношение, связывающее неизвестную решетчатую функцию f() и ее разности до орядка k включительно Разностное уравнение k-го орядка заисывают в виде или в силу формулы (13) F(n, f(), f(), f(),, k f()) = 0 (131) F(n, f(), f( + 1), f( + ),, f( + k)) = 0 (13) Заметим, что ри необходимости неизвестную решетчатую функцию можно обозначать через х(), у(), (n), По аналогии с теорией обыкновенных дифференциальных уравнений од решением уравнений (131) или (13) онимают всякую решетчатую функцию f(), которая ри одстановке ее в уравнение риводит к верному равенству для = 0, 1,, 13 Линейные разностные уравнения Целесообразно рассмотреть одробнее линейные разностные уравнения, которыми оисываются линейные дискретные системы (системы с дискретным воздействием) Линейное разностное уравнение k-го орядка с остоянными коэффициентами имеет вид С 0 k x() + С 1 k 1 x() + + С k x() = φ(n), (133) где С i = const (вещественные), i = 0, 1,, k; C 0 0, x() неизвестная решетчатая функция Уравнение (133) можно заисать в виде а 0 x( + k) + a 1 x( + k 1) + + a k x() = φ(n), (134) где а i = const, i = 0, 1, ; а 0 0, а k 0 Если решетчатая функция φ(n) 0, то уравнения (133), (134) называются однородными; в ротивном случае неоднородными Для уравнений (133), (134) о аналогии с обыкновенными дифференциальными уравнениями может быть сформулирована задача Коши: 6
7 найти решетчатую функцию x(), удовлетворяющую уравнению (134) и условиям x( 0 ) = х 0, x( 0 + 1) = х 1,, x( 0 + k 1) = х k 1, (135) где 0 некоторое начальное значение аргумента ; х 0, х 1,, х k 1, заданные числа Условия (135) называются начальными условиями Если x i 0, i = 0, 1,, k 1, то условия называют нулевыми Заметим, что в случае заиси разностного уравнения в виде (133), начальные условия задаются в виде i ( 0 ) = α i, α i = const, i = 0, 1,, k 1 По аналогии с теорией обыкновенных дифференциальных уравнений имеют место следующие в ункте 14 утверждения 14 Решение линейных однородных разностных уравнений Рассмотрим линейное однородное разностное уравнение k-го орядка с остоянными коэффициентами а 0 x( + k) + a 1 x( + k 1) + + a k 1 x( + 1) + a k x() = 0, (141) где а 0 0, a k 0 Разностное уравнение (141) имеет ровно k линейно независимых частных решений х 1 (), х (),, х k () Общее решение уравнения (141) имеет вид где С 1, С,, С k const х 0 () = С 1 x 1 () + С x () + + С k x k (), Линейно независимые частные решения этого уравнения будем искать в виде х() = λ, где λ 0 некоторое неизвестное число Неосредственной одстановкой редолагаемого решения в уравнение (141) убеждаемся, что это число λ удовлетворяет равенству а 0 λ k + a 1 λ k a k 1 λ + a k = 0, (14) которое называется характеристическим уравнением для разностного уравнения (141) Итак, решетчатая функция х() = λ является решением разностного уравнения (141), если число λ корень характеристического уравнения (14) При этом возможны три случая: 1) характеристическое уравнение (14) имеет ровно k различных действительных корней; ) корни характеристического уравнения различны, но среди них имеются комлексные; 3) среди корней характеристического уравнения имеются кратные 7
8 Рассмотрим эти случаи 1 Пусть λ 1, λ,, λ k действительные и различные корни характеристического уравнения (14) Им отвечают k следующих линейно независимых частных решений (фундаментальная система решений): х 1 () = 1, х () =,, х k () = 8 k (143) В этом случае общее решение линейного разностного уравнения (141) заисывается в виде линейной комбинации фундаментальной системы решений: C i = const, i = 1. k х 0 () = С 1 + С + + С k, (144) 1 Пример 141 Решить разностное уравнение второго орядка x( + ) 5x( + 1) + 6x() = 0 Решение Характеристическое уравнение λ 5λ +6 = 0 имеет корни λ 1 = и λ = 3 Тогда, согласно равенствам (143), частными линейно независимыми решениями уравнения являются функции х 1 () = и х () = 3, а общим решением решетчатая функция х 0 () = С 1 + С 3, C 1, C const Пусть среди различных корней характеристического уравнения (14) имеются комлексно-соряженный корень вида λ = α ± βi Как и в теории линейных дифференциальных уравнений, можно оказать, что если комлекснозначная функция х() = U() + iv(n) является решением линейного однородного разностного уравнения, то функции U() и V(n) также решения этого уравнения Далее нетрудно доказать, что решетчатые функции х 1 () = r n cosnφ; х () = r n sinnφ (145) являются линейно независимыми решениями линейного однородного разностного уравнения (141), отвечающими комлексно-соряженному корню α ± βi характеристического уравнения (14) Общее решение заисывается в виде их линейной комбинации Пример 14 Решить разностное уравнение третьего орядка x( + 3) 4x( + ) + 6x( + 1) 4х()= 0 Решение Характеристическое уравнение имеет корни λ 1 = и λ,3 = 1 ± i Так как λ 3 4λ + 6λ 4 = (λ )(λ λ + ) = 0 λ = 1 + i = 3 i е 4 k 3 3 = cos i sin, 4 4 то согласно формулам (145) числам λ,3 отвечают действительные решения
9 х () = 3 cos 4 Числу λ 1 = отвечает решение х 1 () = и х3 () = 3 sin 4 Итак, общее решение исходного уравнения имеет вид х 0 () = С 1 + С 3 3 cos С3 sin, = 0, 1, Пусть λ корень кратности т характеристического уравнения (14) Тогда ему отвечает т следующих линейно независимых решений: х 1 () =, х () =, х 3 () =,, х т () = Общее решение заисывают в виде их линейной комбинации т1 (146) Пример 143 Найти решение разностного уравнения третьего орядка x( + 3) 3x( + ) + 3x( + 1) + x()= 0 Решение Характеристическое уравнение λ 3 + 3λ + 3λ + 1 = (λ + 1) 3 имеет трехкратный корень λ 1 = λ = λ 3 = 1 Тогда с учетом формулы (146) олучим общее решение исходного разностного уравнения в виде х 0 () = (С 1 + С + С 3 )( 1) Пример 144 Решить начальную задачу: x( + ) x( + 1) 3x() = 0; х(0) = 1; х(1) = 1 Решение Характеристическое уравнение λ λ 3 = 0 имеет корни λ 1 = 1, λ = 3 Тогда общее решение исходного уравнения имеет вид Так как х(0) = С 1 ( 1) 0 + С 3 0 = С 1 + С, х(1) = С 1 ( 1) 1 + С 3 1 = С 1 + 3С, х() = С 1 ( 1) + С 3 то, исходя из начальных условий, олучаем систему из которой С 1 = 1, С = 1 С1 С 1, С1 3С 1, 9
10 Тогда искомым частным решением будет решетчатая функция Z-реобразование 1 Понятие о Z-реобразовании х() = 1 1 ( 1) 3 Пусть
11 является убы- Итак, 1 1 Здесь восользовались фактом, что ри > 1 сумма 1 n 0 вающей геометрической рогрессией Сумма членов убывающей геометрической рогрессии b 1 + b 1 q + b 1 q + b 1 q 3 +, где q ае α > а е α Итак, а ри α = 0: F() = 0 а е = n ае = 0 а е α В частности, если а = 1, олучим е α а ae e a 1 ае 1 ; = ae, Пример 13 Пусть f(n) = а, тогда! F() = а 0! (Исользовали формулу x = е х ) 0! Итак, если > а а n! = е 0! а, = е 11
12 Основные свойства Z-реобразования Рассмотрим лишь основные свойства, которые будут исользованы ри решении задач 1 Свойство линейности Пусть f i (n) F i (), i = 1. k; c i = const, i = 1. k k Тогда ci f i1 i k ( n) cifi ( ) i1 Свойство зааздывания (смещения) Пусть f(n) F(), тогда где f(n k) = 0 ри n k R Если f(n) F(), то df ( ) f(n) d Свойства Z-реобразования: умножение изображений, свертка оригиналов, теорема о редельных значениях можно найти в литературе (см, наример, [] гл 5, 53) 3 Нахождение оригинала о изображению В ростейших случаях восстановить решѐтчатую функцию о ее изображению можно исользуя таблицу основных Z-реобразований и его свойства Рассмотрим сособы нахождения оригинала о его изображению для некоторых ростейших случаев Всомогательные утверждения: 1) точки, в которых нарушается аналитичность функции F(), называются особыми точками; 1
13 ) особые точки, для каждой из которых существует такая ее окрестность, в которой нет других особых точек функции F(), называются изолированными особыми точками; 3) изолированная особая точка 0 ( 0 комлексное число), функции F() называется олюсом, если lim F() = ; 0 P( ) 4) если F() =, где P() и Q() многочлены, то особыми точками Q( ) являются нули знаменателя, то есть корни многочлена Q() Простому (не кратному) корню соответствует ростой олюс, кратному кратный олюс Первый сособ Пусть 1. k особые точки функции F(), лежащие внутри круга = R 1 Тогда решѐтчатая функция f(n) может быть найдена о формуле i n1 k n f(n) = Re s( F( ) 1 ), (31) i1 i n1 i i где Re s( F( ) ) = lim [( ) F( ) ], если i, i = 1. k, ростые олюсы Если F() имеет олюс 0 кратности т, то m1 n1 1 d m n1 Re s ( F( ) ) = lim [( 0) F( ) ] (3) 1 0 ( 1)! m т 0 d Пример 31 Найти решѐтчатую функцию f(n), если ее Z-реобразование F() = ( )( 3)( 1) Решение Функция F() имеет ростые олюсы 1 = 3, = 1, 3 = Значит, на основании формулы (31) имеем: n1 n1 n1 f(n) = Re s ( F( ) ) + Re s ( F( ) ) + Re s ( F( ) ) = 1 n1 = lim [( 3) F( ) ] + lim[( 1) F( ) ] + lim[( ) F( ) ] = = 3 lim 3 ( )( 1) n1 + 1 lim 1 ( )( 3) 3 n1 n1 + lim ( 3)( 1) n1 n1 1 n 1 ( 3) 0 Итак, 3 + n 4 5 f(n) = 1 n 1 ( 3) 0 + n
14 Пример 3 Найти решѐтчатую функцию f(n), если ее Z-реобразование F() = 3 3 ( ) Решение Точка = олюс третьего орядка для функции F() С учетом формулы (3) олучим f(n) = lim ( ) n 1 n1 = ( 3) = 3 ( ) 1 n1 n 1 n n3 = n 3( n 1) = n ( n 1) 3( n 1)( n ) = n( n 1) n 3n( n 1)( n ) n3 = + = ( ) 4 Итак, f(n) = 5( 1) ( 6 5 ) 4 Второй сособ P( ) Пусть F() =, P() и Q() многочлены, стеень числителя меньше Q( ) стеени знаменателя, корни знаменателя ростые Тогда, разложив F() на сумму ростых дробей, наример, методом неоределенных коэффициентов, найдем решѐтчатые функции для каждого слагаемого и восользуемся свойством линейности Z-реобразования Пример 33 Найти решѐтчатую функцию f(n) о известному ее 1 Z-реобразованию F() = 3 Решение Так как = ( + 1)( + ), то функция F() имеет ростые олюсы 1 =, = 1 Разложим F() на сумму ростых дробей: 1 А В = Методом неоределенных коэффициентов находим А =, В = 3 Тогда 1 1 F() = Для нахождения оригинала f(n) восользуемся таблицей, свойствами смещения и линейности Так как а а, а R, то как а = (свойство зааздывания) а а Значит, 1 1 = ( 1) 1 ;
15 Таким образом, F() = 1 = 1 ( ) ( 1) ( ) 1, 1 f(n) = ( 1) ( ) 1 Третий сособ P( ) Пусть F() = равильная дробь и корни знаменателя 1. k Q( ) ростые Тогда решѐтчатая функция f(n) может быть найдена о формуле k Р( i ) n1 f(n) = i (33) i1 Q( i ) Пример 34 Найти решѐтчатую функцию f(n), если F() = Решение Обозначим Р() = +, Q() = = ( + 3)( 1)( ), Q () = 3 7 Так как корни знаменателя ростые (у функции F() ростые олюсы), то n1 n1 n1 f(n) = ( 3) = n 1 = ( 3) 0 Итак, 3 n n 1 5 = 1 n 1 ( 3) n f(n) = 1 n 1 ( 3) 0 + n Применения Z-реобразования 31 Решение линейных разностных уравнений с остоянными коэффициентами и их систем Рассмотрим задачу Коши для линейного разностного уравнения k-го орядка с остоянными коэффициентами: а 0 x( + k) + a 1 x( + k 1) + + a k 1 x( + 1) + a k x() = f(n), (311) х(0) = х 0, х(1) = х 1,, х(k 1) = х k 1, (31) где а i i = 0, 1,, k остоянные коэффициенты, f(n) заданная решѐтчатая функция Требуется найти решение уравнения (311) решѐтчатую функцию x(), удовлетворяющую условиям (31) Будем редолагать, что входящие в уравнение (311) решѐтчатые функции имеют Z-реобразования Построение решения задачи (311), (31) ро- 15
16 ведем о схеме рименения реобразования Лаласа к решению задачи Коши для линейного дифференциального уравнения с остоянными коэффициентами Алгоритм решения задачи 1 Применяем Z-реобразование с учетом его свойств к обеим частям уравнения (311), обозначив x() Х() Решаем олученное алгебраическое уравнение (оераторное) относительно изображения Х() 3 Применяем к Х() обратное Z-реобразование, находим оригинал решѐтчатую функцию x() Замечание Задача Коши для системы линейных разностных уравнений формулируется и решается аналогично Пример 311 Найти решение задачи Коши: х( + ) 4х( + 1) + 4х() =, х(0)=1, х(1) = 6 3 Решение Задано уравнение второго орядка Пусть x() Х(), (из таблиц) ( ) По свойству оережения найдем х( + 1) Х() x(0) = Х() ; х( + ) Х() x(0) x(1) = Х() 6 3 На основании свойства линейности олучим оераторное уравнение относительно функции Х(): Х() 3 4Х() Х() = 6 ( ) Решим оераторное уравнение относительно изображения Х(): Х()( 4 + 4) = + 1, ( ) 6 Х() = 4 + ( ) ( ) 6( ) Найдем оригинал (решѐтчатую функцию) соответствующую Х(): 1 ( )( 1) 4 ( ) 4 6 а (Исользовали формулу таблицы m1 ( a) ( ) т m n n a C, а =, т = 3) ( + 1) (формула 8 таблицы); 16
17 1 6 ) 1 1 (формула 7 таблицы) 6 ( Итак, ( )( 1) 1 x() = + ( + 1) 1 = ( + 1) Пример 31 Найти решение задачи Коши для системы линейных разностных уравнений ервого орядка: (5 1)Х() Y() = 10, 6Х() + (5 13)Y() = 5 Решая систему алгебраических уравнений относительно Х() и Y(), олучим: 5х( + 1) = 1x() + у(), 5у( + ) = 6x() + 13у(), x(0) =, у(0) = 1 Решение Пусть x() Х(), у() Y() х( + 1) Х(), у( + 1) Y() Построим систему оераторных уравнений: 5Х() 10 = 1Х() + Y(), 5Y() 5 = 6Х() + 13Y(), или 3 Х() = +, Y() = 3 ( )( 3) Найдем оригиналы 1, = 3 ; (восользовались формулой а k 1 3 k ); ( a) = ( )( 3) k Р( i ) n1 (восользовались формулой f(n) = i, где P() = ; i1 Q( i ) Q() = ( )( 3)) Итак, x() = + 3, у() =
18 3 Применение Z-реобразования к анализу выходных роцессов линейных дискретных стационарных динамических систем Одной из задач теории автоматического регулирования и уравления является задача изучения реакции динамической системы на входной сигнал, то есть нахождение выходного сигнала В зависимости от формы, в которой оисывается математическая модель динамической системы, выделяют динамические системы: — нерерывные, которые оисываются дифференциальными уравнениями; — дискретные оисываются разностными уравнениями; — линейные и нелинейные оисываются линейными и нелинейными уравнениями; — стационарные и нестационарные оисываются уравнениями с остоянными или еременными коэффициентами; — одномерные и многомерные у многомерных суммарное число входов и выходов больше двух Для решения задач анализа линейных нерерывных одномерных и многомерных стационарных динамических систем рименяется реобразование Лаласа (изучено нами ранее, см [3], [4]) Рассмотрим рименение Z-реобразования для решения задач анализа линейных дискретных одномерных стационарных динамических систем Постановка задачи: 1) задан входной сигнал g(n), n = 0, 1,, ; ) задана одномерная линейная дискретная стационарная динамическая система, оведение которой оисывается в общем случае разностным уравнением вида а k x( + k) + a k 1 x( + k 1) + + a 0 x() = = b m g( + m) + b m 1 g( + m 1) + + b 0 g(); (31) 3) заданы начальные условия х(0) = х 0, х(1) = х 1,, х(k 1) = х k 1, (3) здесь a 0, a 1,, a k ; b 0, b 1,, b m числа, заданные коэффициенты, k m Требуется найти выходной сигнал x() Будем редолагать, что входной сигнал g() и выходной сигнал x(), n = 0, 1. являются оригиналами Применим Z-реобразование к обеим частям уравнения (31) с учетом свойств линейности и оережения Получим оераторное уравнение (a k k + + a 0 )Х() x 0 (a k k + a k 1 k a 1 ) x 1 (a k k 1 + +a ) x k 1 a k = (b m m + + b 0 )G() g(0)(b m m + + b 1 ) g(m 1)b m, (33) где x() Х(), g() G() Обозначим D() = a k k + + a 0, M() = b m m + + b 0, D Н () = x 0 (a k k + + a 1 ) + x 1 (a k k 1 + +a ) + + x k 1 a k ; D g () = g(0)(b m m + + b 1 ) + g(1)(b m m b ) g(m 1)b m 18
19 Тогда уравнение (33) может быть заисано в виде D()Х() = M()G() + D Н () D g () Из оследнего уравнения находим Z-реобразование выходного сигнала: D Х() = Н ( ) D g ( ) + W() G(), (34) D( ) D( ) где функция m М ( ) bm b0 W() = = (35) k D( ) ak a0 является ередаточной функцией Выходной сигнал x() оределяем из уравнения (34) с омощью обратного Z-реобразования Замечание 31 В уравнении (34) ервое слагаемое оисывает движение од действием ненулевых начальных условий и нулевом входном сигнале (свободное движение); второе и третье слагаемые движение од действием входного сигнала ри нулевых начальных условиях (вынужденное движение) Если начальные условия нулевые, выходной сигнал оределяется вынужденным движением Если т = 0, функция D g () = 0, D Х() = M ( ) + W() G() D( ) Если т = 0 и начальные условия нулевые Х() = W() G() Замечание 3 Если ри решении задачи нет необходимости в анализе, розвучавшем в замечании 31, то Z-реобразование выходного сигнала можно найти неосредственным разрешением уравнения (33) относительно Х() Итак, ри решении задач анализа выходных роцессов следует ридерживаться следующего алгоритма: 1) найти Z-реобразование входного сигнала G() = Z
20 Построим ередаточную функцию W() Так как k = 1, m = 0, a 1 = 1, a 0 = 4, b 0 = 4, то M() = 4, D() = 4, то 4 W() = 4 3 Так как х 0 = 0, m = 0, то D Н () = 0, D g () = 0, то 4 Х() = W()G() = 4 ( 1) Найдем выходной сигнал, рименяя обратное Z-реобразование к остроенному изображению Х() Для этого редставим Х() в виде суммы ростых дробей: Х() = 4 = 4 ( 1) ( 1) 1 Исользуя свойства линейности и таблицу, находим x() = 9 4 (4 3 1) Ответ: x() = 9 4 (4 3 1), = 0,, Пример 3 Найти реакцию дискретной динамической системы, оисываемой уравнением x( + ) 5x( + 1) + 6x() = g( + ) 3g( + 1) + g(), на входной сигнал g() = 1 ри начальных условиях x(0) = 1, x(1) = Решение Очевидно, k =, m =, a = 1, a 1 = 5, a 0 = 6, b = 1, b 1 = 3, b 0 = 1 Найдем Z-реобразование входного сигнала: G() = Z <1>= 1 Построим ередаточную функцию W(): b b1 b0 3 ( 1)( ) 1 W() = = = = a a1 a0 5 6 ( )( 3) 3 Оределим D Н () = 3, D() = 5 + 6, D g () = g(0)(b + b 1 ) + g(1)b = 3 + =, g(0) = g(1) = 1 3 Найдем Z-реобразование выходного сигнала о формуле (34): 3 1 Х() = + = (выолнили действия над дробями в равой части соотношения) 4 Найдем выходной сигнал: Ответ: x() =, = 0,, 0
21 Задачи для самостоятельного решения Применяя Z-реобразование, найти решение задач 1 x( + ) 3x( + 1) + x() = 0, x(0) =, x(1) = 3 x( + ) 5x( + 1) + 6x() = 0, x(0) = 1, x(1) = 3 x( + 3) 5x( + ) + 8x( + 1) 4x() = 0, x(0) = 0, x(1) =, x() = 1 4 x( + ) 5x( + 1) + 6x() = g(), g() = 1, x(0) = 0, x(1) = 0 5 х( 1) х( ) у( ), у( 1) 3х( ) 4у( ), x(0) = 3, y(0) = 4 6 х( 1) х( ) 3у( ), у( 1) х( ) у( ), x(0) = 3, y(0) = 1 7 х( 1) у( ) 1, у( 1) 4х( ) 0, x(0) = y(0) = 0 8 x( + ) 5x( + 1) + 6х() = g( + 1) 3g(), g() = 1, x(0) = 1, x(1) = Решить задачу анализа выходных роцессов 9 х( 1) 4х( ) у( ) g( n), g( n) 1, у( 1) х( ) у( ), 7 13 x(0) =, у(0) = 4 4 х( 1) х( ) у( ) 3 10 у( 1) х( ) 3, x(0) = 3, y(0) = 0 Ответы: 1 x() = 1 + ; x() = ; 3 x() = ;, 1
22 4 x() = ; 5 x() = , у() = ; 6 x() = 3 sin + 3 cos, 3 3 y(k) = cos 3 + sin 3 7 x() = ( ) , y() = ( ) 8 x() = ; 9 x() = , у() = x() = ( 1), у() = ( ) + ( 1) 3, = 0, 1, Сисок литературы 1 Жевняк РМ, Карук АА Высшая математика: учебн особие для втузов Ч 4 Минск: Выш шк, с Пантелеев АВ, Якимова АС Теория функции комлексного еременного и оерационное исчисление в римерах и задачах: учебн особие М: Высшая школа с 3 Араманович ИГ, Лунц ГЛ, Эльсгольц ЛЭ Функции комлексного еременного Оерационное исчисление Теория устойчивости М: Наука, Деч Г Руководство к рактическому рименению реобразования Лаласа и Z-реобразования М: Наука, 1971
23 Приложение А Таблица А1 Основные Z-реобразования f(n) F() ( 1) 1 3 е α e 4 a n a 5 a n е α аe а 6! 7 a n 1 ( a) 8 ( + 1)a n ( a) 9 a n sin βn a sin a cos а 10 a n cos βn ( a cos ) a cos а 11 n ( 1) 1 n ( 1) ( 1) 13 n f ( k) F( ) k 0 ( 1) 14 k C n, k = 1,, 1 ( 1) k k а 15 Cn a n т1 ( а) F ( ) 16 f(n k) k a е т 3
24 Продолжение таблицы А1 f(n) F() 17 f(n + k) F( ) i k k nf(n) F () 19 a n f(n) F(a) 0 f(n)*g(n) F()G() f ( i) ki 4
25 Учебное издание РАЗНОСТНЫЕ УРАВНЕНИЯ Z-ПРЕОБРАЗОВАНИЕ И ЕГО ПРИМЕНЕНИЯ Учебно-методическое особие Составители: Подолян Светлана Владимировна Юрченко Ирина Викторовна Редактор АА Щербакова Технический редактор ТВ Багуцкая Подисано в ечать 01 Формат Бумага офсетная Гарнитура Таймс Ризография Услечл Уч-изд Тираж экз Заказ Учреждение образования «Могилевский государственный университет родовольствия» ЛИ 0330/630 от Пр-т Шмидта, 3, 107, Могилев Отечатано в учреждении образования «Могилевский государственный университет родовольствия» Пр-т Шмидта, 3, 107, Могилев 5
Преобразование Лапласа дискретного сигнала. Z-преобразование. Разностное уравнение дискретного фильтра
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
В предыдущих разделах мы подробно рассмотрели расчет аналоговых фильтров с заданными характеристиками. Пришло время переходить к анализу цифровых фильтров. Необходимо разделить понятия дискретного и цифрового фильтра.
Дискретным мы будем называть фильтр, импульсная характеристика которого является дискретной, а коэффициенты передаточной функции рассчитаны точно без ошибок округления.
Под цифровым фильтром мы будем понимать дискретный фильтр, коэффициенты передаточной характеристики которого рассчитаны не точно, а с ошибками округления вызванными конечной разрядностью представления числа.
На практике все рассчитанные фильтры являются цифровыми, так как разрядность представления числа ограничена. Однако использование компьютера позволяет производить операции с 64-битными числами с плавающей точкой, что минимизирует ошибки округления, поэтому можно предполагать, что рассчитанные с такой разрядностью фильтры «почти дискретные».
Важно отметить, что округление коэффициентов устойчивого дискретного фильтра, даже самое незначительное, может привести к неустойчивому цифровому фильтру. Поэтому при расчете фильтров, особенно фильтров высокого порядка, всегда необходимо проверять их устойчивость.
В цифровых системах сигналы представляют собой последовательности отсчетов, взятые, как правило, через равные промежутки времени . Ранее мы уже рассматривали модель дискретного сигнала :
Графически процесс дискретизации сигнала показан на рисунке 1.
Рассмотрим преобразование Лапласа дискретного сигнала :
Важное замечание. Если , то получаем дискретно-временное преобразование Фурье дискретного сигнала, при этом является периодической функцией частоты с периодом , кроме того, если , то
Кружочками условно показаны нули образа , а крестиками — полюсы.
Важно отметить, что периодичность дискретного преобразования Лапласа соответствует периодичности преобразования Фурье дискретного сигнала . Однако, как мы знаем из теории дискретного преобразования Фурье, на каждом периоде повторения спектр дискретного сигнала может быть искажен эффектом алиасинга, т.е. наложением «хвостов» исходной спектральной плотности из высших зон Найквиста (заполненная точками область на карте нулей и полюсов образа соответствует высшим зонам Найквиста).
В случае дискретного преобразования Лапласа эффект алиасинга сохраняется, и периодический образ на каждом периоде отличается от исходного образа . Так например, мы можем наблюдать алиасинг полюсов из высших зон Найквиста при неверном выборе частоты дискретизации. Если все полюсы исходного образа попадают в первую зону Найквиста, то при дискретизации они периодически разможатся, как это показано на рисунке 2.
Положение нулей дискретного преобразования Лапласа , как правило отличается от положения нулей исходного образа в результате эффекта алиасинга.
Рассмотрим процесс фильтрации дискретного сигнала . Согласно свойству преобразования Лапласа, процесс фильтрации во временно́й области сводится к умножению образа исходного сигнала на передаточную характеристику фильтра , которая в свою очередь, представляет преобразование Лапласа импульсной характеристики фильтра . Тогда преобразование Лапласа сигнала на выходе фильтра можно записать:
Первый случай. — образ дискретного сигнала, удовлетворяет (3), а — передаточная характеристика непрерывного фильтра, и свойство (3) не выполняется, значит также не удовлетворяето (3). Тогда можно сделать вывод о том, что при прохождении дискретного сигнала через аналоговый фильтр, выходной сигнал получается аналоговым. Аналоговый фильтр производит восстановление непрерывного сигнала по имеющемуся дискретному.
Второй случай. удовлетворяет (3), также удовлетворяет (3) (импульсная характеристика фильтра является дискретной), причем интервалы дискретизации сигнала и фильтра одинаковые и равны . Тогда в результате произведения также удовлетворяет (3). Таким образом, при прохождении дискретного сигнала через дискретный фильтр, выходной сигнал получается дискретным, с той же частотой дискретизации.
Третий случай. и удовлетворяют (3), но интервал дискретизации сигнала равен , а интервал дискретизации импульсной характеристики фильтра (исходный сигнал и и импульсная характеристика фильтра дискретизированы с разной частотой). В этом случае , в частных случаях, может удовлетворять (3), но период дискретизации выходного сигнала , будет равен «наименьшему общему кратному» периодов и . Заметим, что термин «наименьшее общее кратное» взят в кавычки, потому что и могут быть вещественными числами, в том числе и иррациональными. Тогда понимается как вещественное число, которое делится нацело как на , так и на . Например, если , а , то . Данный на практике не встречается, так как требует реализации цифровых схем, работающих на разных тактовых частотах. Разработка таких схем сопряжена с трудностями синхронизации при переходе данных из модулей, работающих на различных тактовых частотах.
Основное правило — для дискретных и цифровых фильтров интервалы дискретизации сигнала и фильтра должны быть равны.
Таким образом, для того чтобы на выходе фильтра получить дискретный сигнал, необходимо чтобы импульсная характеристика фильтра также была дискретной, а значит передаточная характеристика дискретного фильтра может быть представлена как результат дискретного преобразования Лапласа:
Если у дискретного фильтра количество коэффициентов ограничено, то такой фильтр называют фильтром с конечной импульсной характеристикой (КИХ-фильтром) [1] , а если количество коэффициентов бесконечно, то такой фильтр называют фильтром с бесконечной импульсной характеристикой (БИХ-фильтр) [2] .
При переходе от аналогового фильтра к цифровому, происходит периодическое размножение передаточной характеристики вдоль оси . При этом, переменная в образах дискретного преобразования Лапласа всегда присутствует только в показателе экспоненты, для обеспечения периодичности передаточных характеристик дискретных систем [1, стр 155].
В результате периодизации также происходит периодическое размножение нулей и полюсов, что доставляет некоторые неудобства. Для облегчения анализа вводят переменную вида:
Отображение не является конформным [2, стр. 145], потому что множество точек плоскости отображается в одну точку плоскости .
Графически отображение -плоскости в комплексную -плоскость показано на рисунке 3.
Рассмотрим некоторые особенности отображения (7).
Если , где , то для всех этих точек .
Если чисто вещественно, то и также вещественное, причем 0″/>. Заметим, что при , (внутри единичной окружности), а при величина (вне единичной окружности).
При , точка на мнимой оси плоскости отображается в точку , расположенную на единичной окружности и повернутой на угол рад. Таким образом, вся мнимая ось плоскости отображается в единичную окружность плоскости . Причем, один оборот единичной окружности соответствует от до рад/c.
Левая полуплоскость комплексной плоскости отображается внутрь единичной окружности плоскости . Действительно если , то представляет вектор длины повернутый на угол рад. При , длина вектора .
Правая полуплоскость комплексной плоскости отображается вне единичной окружности плоскости .
При переходе из комплексной -плоскости в комплексную -плоскость все бесконечно-повторяющиеся нули и полюса дискретного фильтра в -плоскости отображаются в конечное количество нулей и полюсов в -плоскости. Тогда выражение для передаточной характеристики дискретного фильтра может быть представлено при помощи подстановки (7) через конечное количество нулей и полюсов в -плоскости как:
Таким образом, главный вывод, который мы должны сделать заключается в следующем: при переходе от аналогового фильтра к дискретному, образ по Лапласу становится периодическим по мнимой оси, а количество нулей и полюсов фильтра бесконечным. Но при переходе в комплексную –плоскость мы получаем снова конечное количество нулей и полюсов, и соответственно конечное количество коэффициентов дискретного фильтра.
Рассмотрим некоторые свойства -преобразования. При этом мы будем рассматривать свойства относительно индексов отсчетов в предположении . В результате мы можем опустить период дискретизации в выражениях -преобразования.
Линейность. -образ суммы двух сигналов равен сумме -образов этих сигналов. Действительно, пусть есть два дискретных сигнала и , . Найдем -преобразование их суммы :
Можно показать, что данное свойство также справедливо и для циклической задержки ограниченной выборки сигнала:
Теорема о свертке. Пусть дано два сигнала ограниченной длительности и , . Найдем -преобразование их циклической свертки :
При выводе было использовано свойство циклической задержки -преобразования. Таким образом циклическая свертка сигналов соответствует произведению их -образов.
Аналогично, используя свойство задержки, можно показать, что -образ линейной свёртки сигналов равен произведению их -образов:
Ранее мы говорили о том, что пассивные аналоговые цепи описываются интегро-дифференциальными уравнениями непрерывного времени . При этом математический аппарат преобразования Лапласа позволяет перейти к алгебраическим уравнениям комплексной переменной при описании характеристик комплексных сопротивлений двухполюсников и передаточных функций четырехполюсников.
Ограничение количества пассивных элементов аналогового фильтра приводит к ограничению порядков интегро-дифференциальных уравнений и, соответственно, полиномов переменной при описании передаточных характеристик.
Прохождение сигнала через аналоговый фильтр описывается интегралом свертки входного сигнала и непрерывной импульсной характеристики , которая в свою очередь не может иметь произвольную форму при ограничении порядка аналогового фильтра, потому что является результатом решения интегро-дифференциальных уравнений ограниченного порядка.
Дискретные системы, в свою очередь, описываются разностными уравнениями дискретного времени . По аналогии с аналоговыми фильтрами, мы не можем требововать бесконечных порядков разностных уравнений, потому что это потребует бесконечных вычислительных ресурсов. Таким образом, мы должны ограничить порядки разностных уравнений, которые связывают выходной сигнал дискретного фильтра с входным сигналом , а также со значениями выходного сигнала на предыдущих тактах .
Заметим, что здесь мы также ведем рассмотрение относительно индексов отсчетов сигналов, в предположении c.
Общее разностное уравнение линейного цифрового фильтра имеет вид:
Временной индекс изменяется от до бесконечности, т.к. предполагается, что фильтр после включения может работать неограниченно долго.
Рассмотрим -преобразование разностного уравнения (16). -образ выходного сигнала равен:
Решение обыкновенных линейных разностных уравнений с постоянными коэффициентами
Страницы работы
Содержание работы
Решение обыкновенных линейных разностных уравнений
с постоянными коэффициентами
Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами
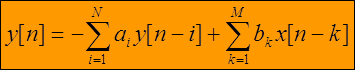
где y[n]— выходной сигнал в момент n,
x[n] — входной сигнал в момент n,
Для решения таких уравнений могут использоваться два метода
- Прямой метод,
- Метод Z – преобразования.
Вначале рассмотрим решение линейного разностного уравнения с помощью прямого метода.
Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения
Общее решение однородного разностного уравнения (zero-input response) yh[n]
определяется в виде
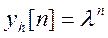
Подставляя это решение в однородное уравнение, получаем
или 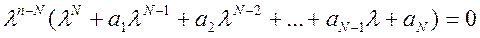
Такой полином называют характеристическим полиномом системы. Он имеет N корней 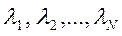
Если корни 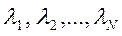
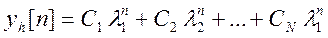
где коэффициенты 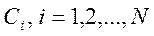
Если некоторый корень, например, λ1 имеет кратность m, то соответствующий ему член решения приобретает форму
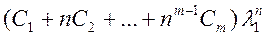
Если все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням 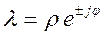
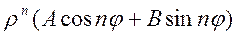
Вид частного решения yp[n] уравнения зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице
Таблица 1. Вид частного решения для различного характера правой части
Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности и временного сдвига. В результате получается линейное алгебраическое уравнение относительно Z — изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.
Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.
Пример. Определим отклик (выходной сигнал) системы, описываемой линейным разностным уравнением 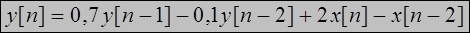
1. Прямой метод решения уравнения.
Однородное уравнение 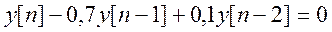
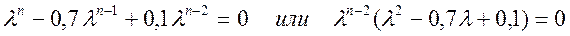
Корни полинома 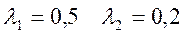
Решение однородного уравнения 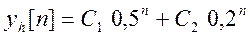
Поскольку ,то частное решение определяем в виде 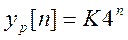
Подставляем его в уравнение
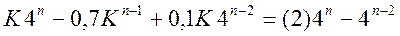
Для нахождения константы К примем n = 2. Тогда
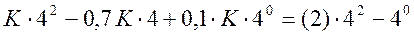
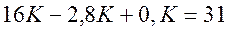
Отсюда частное решение 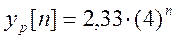
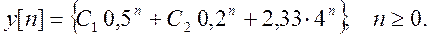
Найдем константы С1 и С2. Для этого положим n = 0, тогда из исходного разностного уравнения получаем 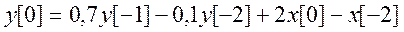
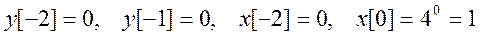
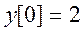
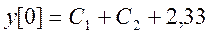
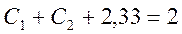
Далее положим n = 1, при этом из уравнения следует 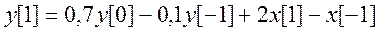
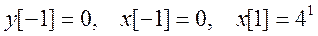
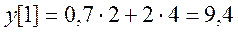
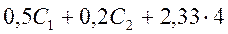
Получаем следующие два уравнения для С1 и С2
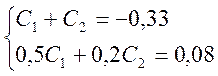
Решение этой системы дает следующие значения: С1 =0,486 и С2 = -0,816.
Следовательно, общее решение данного уравнения
2. Решение методом Z – преобразования.
Возьмем Z – преобразование от исходного разностного уравнения 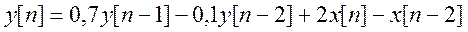
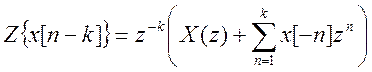
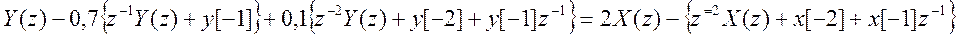
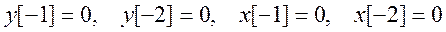
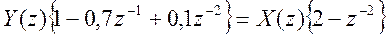
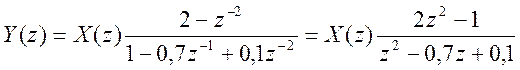
Для данного случая 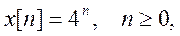
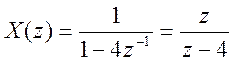
Подставляя его в предыдущее выражение, получаем решение уравнения в Z – области
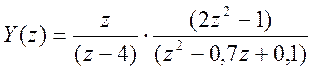
Найдем корни полинома
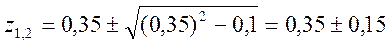
Для получения решения уравнения во временной области представим Y(z) в виде суммы элементарных дробей
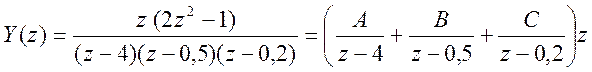
Определим коэффициенты A, B, C
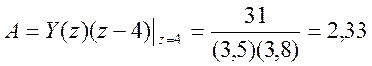
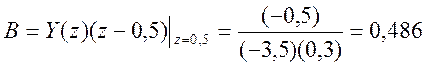
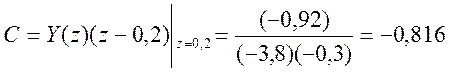
Поэтому представление Y(z) как суммы элементарных дробей имеет вид
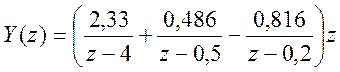
Обратное Z – преобразование от 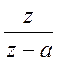
Следовательно, решение уравнения во временной области имеет вид

http://ru.dsplib.org/content/filter_ztransform/filter_ztransform.html
http://vunivere.ru/work11372