Задача дирихле для уравнения пуассона в круге

Численные методы решения уравнений эллиптического типа

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

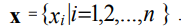
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

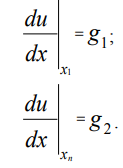
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

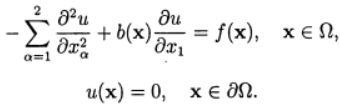
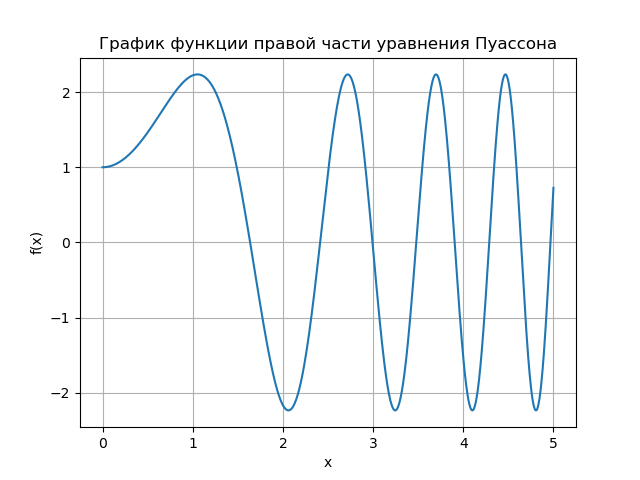
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

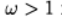
На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

Лекция 10. Метод функций Грина решения задачи Дирихле

Метод функций Грина решения задачи Дирихле основывается на формулах Грина. На плоскости эта формула имеет следующий вид: если функции U = U(x,y) и V = V(x,y) имеют непрерывные частные производные второго порядка в ограниченной области D и непрерывны в замкнутой области , то

где и — производные по направлению внешней нормали к D, а кривая Г — положительно ориентирована (то есть направление интегрирования таково, что область D при интегрировании остается слева). Из этой формулы легко выводится обобщенная формула Грина

где С — замкнутая кривая, лежащая внутри кривой Г,а D — область, заключенная между Г и С (см. рис. 20). Кривая С также положительно ориентирована, а n₁ — направление внешней нормали к D.

Аналогичная формула имеется и в случае пространства, однако мы ее не приводим, поскольку в дальнейшем метод функций Грина подробно излагается только для плоских областей. Для искомой гармонической функции U , удовлетворяющей условию Дирихле , и функции V = G(P, P_o) — функции Грина — формула (43) будет иметь вид:

где С — окружность радиуса ε с центром в точке P_o (см. рис.20). Остальные слагаемые в данном случае будут равны нулю, так как и в D. Вычислим интеграл Для этого введем полярные координаты (r, φ) с полюсом в точке P_o. Тогда на окружности C расстояние r = ε и dl = εdφ. Поэтому

Из определения функции Грина вытекает, что где g(P, P_o) — гармоническая функция всюду в области D. Это означает, что g(P, P_o) и ее производная по нормали n₁ ограничены в D, следовательно

Кроме того, функция U и ее производная — также ограничены в D. Поэтому

где α(ε) и β(ε) — ограниченные величины при

Переходя к пределу при , получим

Таким образом, из формулы (44) с учетом граничного условия вытекает

Эта формула дает решение задачи Дирихле для ограниченной области на плоскости, если известна функция Грина G.

В пространстве доказывается аналогичная формула, дающая интегральное представление решения задачи Дирихле, если известна соответствующая функция Грина. Она имеет вид

где Г — положительно ориентированная поверхность, ограничивающая область D в пространстве, и ,f(s) — граничные значения гармонической функции.

Замечание. Метод функций Грина позволяет получать решения многих задач в областях различной формы. Однако для каждой области (а точнее, для каждого оператора, стоящего в левой части граничного условия) и для каждого уравнения нужно находить свою функцию Грина, что является часто непростой задачей. В том случае, когда функция Грина известна, например, для круга, шара или других простых областей (см. лекцию 9), решение соответствующей задачи выводится несложными вычислениями.

С помощью формулы (45) легко получается интегральная формула Пуассона для круга. Для этого нужно вычислить производную функции Грина для круга. Рассмотрим сначала круг радиуса R с центром в начале координат (см. рис.17). Функция G(P, P_o) для этого круга имеет вид (формула 42):

Так как направление внешней нормали к Г совпадает с направлением полярного радиуса ρ , то

На границе Г расстояние поэтому

Подставим полученное выражение для производной в формулу (45):

Так как точка может быть произвольной внутри круга, обозначим ее координаты через — полярная система координат с полюсом в точке О. Тогда окончательно формула (46) примет вид:

Из формулы (47) нетрудно получить интегральную формулу Пуассона для произвольного круга радиуса R с центром (х_о , у_о). Для этого преобразуем данный круг с помощью замены переменных в круг того же радиуса, но с центром в начале координат, запишем для него формулу (47), а затем вернемся к прежним переменным. В результате будем иметь формулу

Функция называется ядром Пуассона для круга. Отметим некоторые свойства ядра Пуассона.
1. Ядро Пуассона положительно при ρ

Свойство 1 очевидно, так как . На луче α = φ ядро Пуассона имеет вид

Свойства 2 и З проверяются непосредственно с помощью вычислений. Однако свойство 3 можно доказать и более красивым способом. А именно, если рассмотреть задачу Дирихле в круге радиуса R с граничным условием , то решение такой задачи определяется формулой Пуассона (47):

С другой стороны, функция также является решением задачи Дирихле в круге с тем же граничным условием. В силу единственности решения задачи Дирихле получаем равенство (48).