Задача дирихле и неймана для уравнения лапласа

Граничные условия. Задачи Дирихле и Неймана

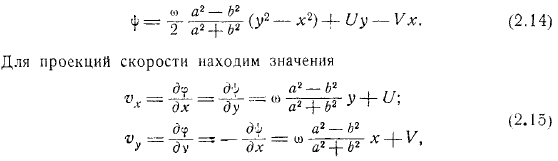
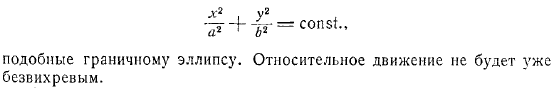
Граничные условия. Задачи Дирихле и Неймана

Поиск комплексного потенциала, определяющего планарное невращательное движение несжимаемой жидкости гидромеханики, можно свести к поиску функции потока, поскольку потенциал связан с известными условиями Коши. Римана, из известной функции можно определить в виде квадратуры. Функция потока, которая считается непрерывной во всех точках течения несжимаемой жидкости, удовлетворяет уравнению Лапласа в этих точках, а на определенных границах течения-некоторым известным условиям. Формат зависит от реализации квартиры.

Показаны простейшие случаи, без цели исчерпывающей классификации различных типов граничных условий. Рассматривая плоское течение бесконечно статичной бесконечной жидкости о движении тела в идеальной жидкости, возникающее при движении цилиндра, граничные условия для функции потока однозначно следующие — поскольку скорость в этих точках должна быть равна нулю. В каждой точке контура движущегося тела, нормальная проекция скорости должны совпадать.

• Угол между элементом линии потока и осью, а соотношение между позволяет выразить рассматриваемое условие. И если в жидкости еще есть неподвижный объект, то по их контуру понятно, что обычная составляющая скорости соседних частиц жидкости должна быть равна нулю, другими словами, сам неподвижный контур должен находиться в контакте с текущей линией. В этом случае необходимо добавить граничное условие к предыдущему условию. Для точки фиксированного контура.

Если тело движется поступательно со скоростью, направленной вдоль оси, то условие равно. Принять форму, или все точки контура, после того как цилиндрический объект совершает какое-либо движение. При наличии поступательного потока с бесконечно большой скоростью расстояние до удаленной точки равно, ориентированной вдоль оси и обтекающей неподвижный объект. Граничное условие, очевидно, выглядит так: для бесконечности показанные нами граничные условия в основном используются при исследовании стационарного движения, но остаются справедливыми для нестационарного потенциала.

В этом случае предыдущее выражение вводит только время в качестве параметра. Параметры зависят от. Известное значение функции на контуре области называется задачей Дирихле, хотя это задача определения функции, удовлетворяющей уравнению Лапласа в области. Таким образом, мы видим, что определение плоского невращательного движения несжимаемой жидкости, вызванного движением контура, ограничивающего область течения, приводит к решению конкретной задачи Дирихле.

При решении гидродинамических задач можно также сначала найти все потенциалы скорости. Он также должен удовлетворять уравнению Лапласа в области течения. Но является ли граничное условие схемы необходимым для функции? Другой само определение потенциала скорости является вертикальной проекцией в скорости частицы жидкости, прилегающие к контуру, и, следовательно, граничное условие для функции принимает форму an является нормальной проекции скорости точки контура. В частности, в терминах фиксированных границ, мы получим условие.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Людмила Фирмаль

В области, задача определения функции, которая удовлетворяет уравнению Лапласа по известному значению нормальной производной функции на контур области называется задачей Неймана. Поэтому гидродинамические задачи приводят к решению некоторых задач Неймана. Вы можете использовать функцию для определения функции и наоборот. Поэтому ясно, что задача Неймана может быть сведена к задаче Дирихле, или наоборот. Факт, запомните состояние Коши-Римана и проследите за цифрой некоторое время.

Направление нормали в направлении оси, и направление касательной в направлении оси, получаем следующие соотношения сразу, вы можете перейти к задаче Неймана из задачи Дирихле, если есть проблема Неймана, то есть, если вы знаете значение на схеме, это будет следующим образом. Переходим к границе области течения, и поэтому Дирихле. В случае задачи многосвязной области с границей на контуре предыдущее выражение отображает значение аддитивной постоянной для каждой схемы. По значению одной из этих аддитивных констант движение определяется значением производной функции, поэтому его можно выбрать.

Любые константы в будут отображаться. Дана циркуляция скоростей по контуру, которые неприводимы друг к другу. Это полностью совпадает с замечанием о том, что вращательные движения, сделанные в конце раздела главы движение кругового цилиндра , полностью определяются задачей. И цикл только в том случае, если настройка циклическая. В качестве простого примера рассмотрим задачу о невращательном движении несжимаемой жидкости, заключенной в эллиптический цилиндр. Пусть эллиптическое уравнение.

• Его движение характеризуется проекцией на координатную ось скорости и угла поворота скорости его центра. Тогда функция потока должна удовлетворять уравнению в эллипсе и граничному условию самого эллипса. Полином порядка. Я ищу функцию в виде. Уравнение представляет собой отношение. Уравнение из условия является результатом. Это означает связь между для проекции скорости найдите значение, вы можете получить оттуда легко.

Простейший случай чистого поступательного движения цилиндра, когда, выглядит так: то есть жидкость движется вместе со всем цилиндром. Для чистого вращения, когда, это выглядит так: линия потока абсолютного движения гиперболическая. Подчеркнем, что полученная нами формула определяет абсолютное движение жидкости, но относится к движущимся координатным осям.

Движение жидкости относительно этих движущихся координатных осей определяется вычитанием проекции переносной скорости из проекции абсолютной скорости. В результате проекция относительной скорости выглядит следующим образом и представляет собой эллипс, аналогичный граничному эллипсу. Относительное движение больше не является вихревым.

В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Карташов Эдуард Михайлович

Описан новый подход в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости . В основе метода лежит построение «усеченной» функции Грина , что является достаточным для записи аналитического решения задачи.

Похожие темы научных работ по математике , автор научной работы — Карташов Эдуард Михайлович

A new approach in method of green’s functions to the solution of dirichlet and newmann boundary value problems for the laplace equation

A new approach to the application of method of Green»s functions in the Solution of D/r/chlet and Newmann Boundaгу Value Problems for the 2D Laplace equation.

Текст научной работы на тему «О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа»

О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа

Московский государственный университет тонких химических технологий им. М.В. Ломоносова, Москва, 119571, Россия

Описан новый подход в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости. В основе метода лежит построение «усеченной» функции Грина, что является достаточным для записи аналитического решения задачи.

Ключевые слова: уравнение Лапласа на плоскости, задачи Дирихле и Неймана, функция Грина, интегральные записи аналитических решений.

Введение. Уравнения эллиптического типа, к которому относится уравнение Лапласа, играют важную роль в приложениях. К ним приводят задачи о потенциальном движении несжимаемой жидкости, потенциале электростатического поля, стационарных тепловых и диффузионных процессах, потенциальном поле тяготения, а также задачи аэромеханики, теории упругости, электромагнетизма, дифракции и др.

Для линейных эллиптических уравнений второго порядка и, в частности, для уравнения Лапласа задачи Дирихле и Неймана являются основными краевыми задачами. Они детально разобраны в многочисленных руководствах по математической физике, в монографиях по теории ньютоновского потенциала, публикациях, касающихся применения соответствующих интегральных соотношений к изучению конкретных физических процессов. Для нахождения точных решений указанных задач существуют различные аналитические подходы, в основе которых лежат: теория потенциала и метод интегральных уравнений, метод отражения, метод конформных отображений, метод разделения переменных, метод интегральных преобразований, основанный на теории спектральных задач, метод разложения искомого решения в соответствующие ряды, функции единичных источников и диполей 4. И как это ни странно, но в столь, казалось, завершенной области математической физики еще остались «математические резервы» для переосмысления основ некоторых развитых аналитических подходов, в частности, метода функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа на плоскости. Следствием последнего является существенное сокращение технических трудностей, связанных с нахождением

точных аналитических решений классических краевых задач Дирихле и Неймана для уравнения Лапласа. Последнее касается ряда областей, наиболее часто встречающихся в практических приложениях: бесконечная или полубесконечная полоса, полуплоскость или ее четверть, прямоугольник, круг или его внешность, части круга, кольцо, области в параболической, эллиптической и биполярной системах координат. Следует подчеркнуть, что двумерные задачи Дирихле и Неймана могут быть точно решены только для сравнительно простых областей [6]. Полученные в настоящей статье результаты позволяют предвидеть интересные перспективы в дальнейшем развитии аналитической теории краевых задач для уравнений эллиптического типа.

Постановка задачи. Пусть Б — конечная или частично ограниченная выпуклая область изменения М(х, у); Г — кусочно-гладкий контур, ограничивающий область Б; п — внешняя нормаль к Г, вектор, непрерывно меняющийся на Г. В области Б ищется гармоническая функция Т(х,у)е С2 (Б)пС0 (Б), §гаёЫ Т(Ы)е С0 (Б)х

х(( = Б + Г), удовлетворяющая уравнению Лапласа внутри Б

а на границе Г граничным условиям вида (задача Дирихле)