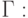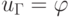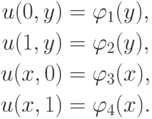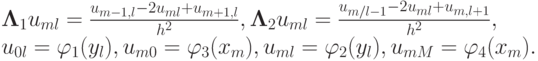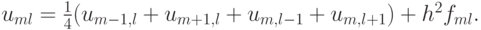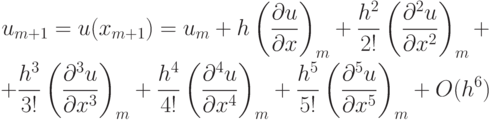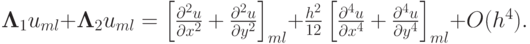Задача коши для эллиптического уравнения

Численные методы решения уравнений эллиптического типа

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

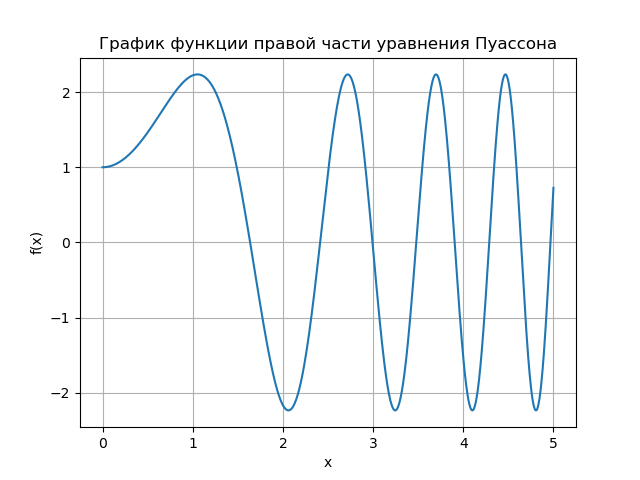
Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

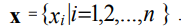
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

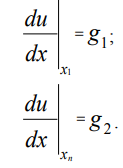
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

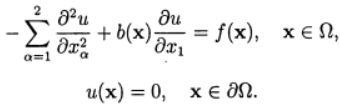
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

Задача Коши для одного класса эллиптических уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Кибирев Владимир Васильевич

Доказаны две теоремы о решении задачи Коши в целом и для одного специального класса уравнений за счет того, что уравнение рассматривается в комплексной области.

Похожие темы научных работ по математике , автор научной работы — Кибирев Владимир Васильевич

Cauchy problem for one class elliptic equations

Two theorems have been proved on the solution of Cauchy problem on the whole and for one special class equations due to the fact that the equation is considered in the complex domain.

Текст научной работы на тему «Задача Коши для одного класса эллиптических уравнений»

ЗАДАЧА КОШИ ДЛЯ ОДНОГО КЛАССА ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ

Доказаны две теоремы о решении задачи Коши в целом и для одного специального класса уравнений за счет того, что уравнение рассматривается в комплексной области.

Ключевые слова: задача Коши, голоморфные функции, полицилиндрическая область, аналитические коэффициенты.

CAUCHY PROBLEM FOR ONE CLASS ELLIPTIC EQUATIONS

Two theorems have been proved on the solution of Cauchy problem on the whole and for one special class equations due to the fact that the equation is considered in the complex domain.

Keywords: Cauchy problem, holomorphic functions, polycylindrical domain, analytic coefficients.

Классическая теорема Коши-Ковалевской дает существование и единственность решения задачи Коши для дифференциального уравнения в частных производных с аналитическими коэффициентами. Однако существование решения гарантируется только в малом. Здесь будет изучаться задача Коши для одного узкого класса уравнений, но решение будет получено и в целом. Решение в целом получается за счет того, что уравнение рассматривается в комплексном пространстве.

где L(u) = (х1. xm)-, причем при вещественных значе-

ниях переменных x1, x2. , xm коэффициенты Ajl вещественны и уравнение (1) эллиптично. Все коэффициенты Л>1 аналитичны в некоторой области голоморфности В из пространства Cm m независимых комплексных переменных x1,x2. xm . Точку x1,x2. xm пространства Cm иногда для краткости обозначаем Х.

Задачу Коши будем изучать в следующей постановке: найти голоморфное решение и уравнения (1), удовлетворяющее условиям

и|,=0 = I (X), £1.=0 = Е (X), (2)

где I и е — функции, голоморфные в некоторой области голоморфности А ^ В из пространства Ст : <. = 0>.

Доказательство основных теорем

Пусть область голоморфности начальных данных (2) А является полицилиндром В : <| /2п(п + 1)М1 )2п.М,

Из оценки (7) следует, что ряды (5) сходятся абсолютно и равномерно в круге

Порядок суммирования и интегрирования здесь можно менять в силу тех же соображений, что и в случае уравнения Лапласа. Функции О и Н относительно переменных г, х1. хт являются решениями уравнения (1).

Так как эти функции удовлетворяют соотношению О =-, области их

Точно таким же образом получается следующее представление для решения задачи Коши в случае, когда вместо кругового полицилиндра О областью голоморфности начальных данных/и g является произвольная полицилиндрическая область Р:

где В — остов границы Р.

Для решения задачи Коши можно дать формулу другого вида. Пусть А — произвольная, ограниченная область пространства С и функция / е Ь2(А), т.е. интегрируема с квадратом модуля по области А. Всякую голоморфную в А функцию / е Ь (А) можно представить как

где К(X, Т) — керн-функция области А, а da — элемент объема в

Воспользовавшись формулой (11), точно так же, как выше использовалась интегральная формула Коши, для решения задачи Коши получим следующее представление:

и(г, X) = ||р(г, X, ШТ) + 8Р&£,Т) /(Т)^, (12)

Р (г, X ,Т ) = у (-1)» __ Ь» (К (X, Т)), «=0 (2» +1)!

т.е. Р (г, X, Т) является решением уравнения (1), удовлетворяющим условиям

Р(0, X, Т)=о, др (^ X ,Т) | ^=о = к (X ,Т).

В частности, для полицилиндра D имеем

_ Г2 Г2 Ш 7 2″+1 1

F ( 7, X, T ) = У (-1)n —-Ln (—)

nm tT (2n +1)! \rx — xltl). (rm -xmtmУ

а для гипершара —

m!R2 » _ 72n+1 г — n»m_1

F ( 7, X, T ) = — у (-1)n —- Ln ( nm n=0 (2n +1)!

Таким образом, воспользовавшись формулой (10), получим две теоремы.

Теорема 1. Существует область голоморфности H(D) из пространства Cm+1 такая, что каковы бы ни были начальные данные fug, голоморфные в полицилиндре D и непрерывные в замкнутом полицилиндре D , решение задачи Коши голоморфно в области H(D).

Теорема 2. Если начальные данные аналитически продолжимы из D, то решение задачи Коши аналитически продолжимо из области H(D). Для каждой точки Х границы В области H(D) существует решение уравнения (1), голоморфное в H(D), удовлетворящее начальным данным, голоморфным в D, и имеющее особенность в точке Х.

Итак, нами получено решение задачи Коши в целом для некоторого класса эллиптических уравнений за счет того, что уравнение рассматривается в комплексной области.

1. Бицадзе А.В. Краевые задачи для эллиптических уравнений второго порядка. — М.: Наука, 1966. — 204 с.

2. Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. — М.: Гостехиздат, 1950. — 436 с.

3. Фукс Б.А. Специальные главы теории аналитических функций многих комплексных переменных. — М.: Наука, 1962. — 420 с.

4. Янушаускас А. К задаче Коши для уравнения Лапласа с тремя независимыми переменными // Сиб. матем. журнал. — 1975. — Т. 16, №6. — С. 1352-1363.

5. Янушаускас А. К теории вырождающихся эллиптических уравнений // Сиб. матем. журнал. — 1974. — Т. 15, №6. — С. 1394-1405

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .

6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»

Будем рассматривать двухмерное уравнение Пуассона

в единичном квадрате 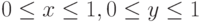с краевыми условиями первого рода на границе расчетной области

( — заданная на границе функция ).

В случае прямоугольной области граничные условия удобно записать в следующем виде:

Для простоты выкладок введем равномерную расчетную сетку с узлами m, y_l> , m, l = 0, 1, . , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию < u_ml >. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.

Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

где h — шаг по координатам, или в операторной форме

Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:

Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.

Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:

Здесь учтено разложение проекции точного решения в ряд Тейлора

и аналогичное разложение для u_{m — 1}.

Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки

Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.

Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.