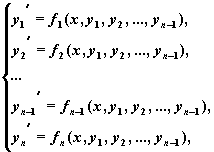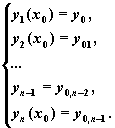Задача коши система уравнений mathcad
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
 |  |
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
 |
 |
 |
| подробная информация о функции odesolve, примеры |
| подробная информация о функциях, примеры |
ODESOLVE
Встроенная функция odesolve предназначена для решения дифференциальных уравнений, линейных относительно старшей производной. В отличие от других функций библиотеки Differential Equation Solving, odesolve решает дифференциальные уравнения, записанные в общепринятом в математической литературе виде.
- Функция odesolve решает для уравнений вида
a(x) y(n) + F(x, y, y’ , . y (n-1) )=f(x)
задачу Коши
y(x0 )=y0 , y'(x0 )=y0,1 , y»(x0 )=y0,2 , . y (n-1) (x0 )=y0,n-1
или простейшую граничную задачу
y (k) (a)=ya,k , y (m) (b)=yb,k , 0 + ), а для записи производных можно использовать как оператор дифференцирования, так и знак производной, например, вторую производную можно вводить в видеили в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.
- Для того чтобы вывести в рабочий документ значения решения в любой точке промежутка интегрирования, достаточно ввести имя функции Y, указать в скобках значение аргумента и знак равенства.
- Значения решения в любой точке промежутка интегрирования можно использовать в дальнейших вычислениях, достаточно ввести в нужном месте имя функции Y, указав в скобках значение аргумента.
Полную информацию о правилах использования функции odesolve можно получить во встроенном справочнике Mathcad в разделе Overview fnd Tutorials.
Функции для решения систем, записанных в нормальной форме
Встроенные функции Mathcad, предназначенные для решения задачи Коши и граничных задач, решают их для нормальных с и с т е м обыкновенных дифференциальных уравнений. Задачи для уравнений высших порядков сводятся к соответствующим задачам для нормальных с и с т е м.
Рассмотрим задачу Коши:
Численное решение этой задачи состоит в построении таблицы приближенных значений
yi,1 , yi,2 , . yi,N
решения y1 (x), y2 (x), . yN (x)
на отрезке [x0 , xN ] в точках
x1 , x2 , . xN, которые называются узлами сетки.
Обозначив
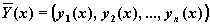
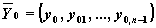
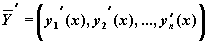
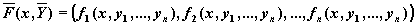
где 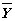
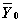
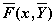
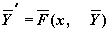
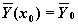
В Mathcad решить задачу Коши для такой системы можно с помощью следующих функций:
- rkfixed(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с постоянным шагом;
- Rkadapt(y, x1, x2, npoints, D) —решение задачи на отрезке методом Рунге—Кутты с автоматическим выбором шага;
- rkadapt(y, x1, x2, acc, npoints, D, kmax, save) —решения задачи в заданной точке методом Рунге-Кутты с автоматическим выбором шага;
- Bulstoer(y, x1, x2, npoints, D) —решение задачи на отрезке методом Булирша-Штера;
- bulstoer(y, x1, x2, acc, npoints, D, kmax, save) —решение задачи в заданной точке методом Булирша—Штера;
- Stiffr(y, x1, x2, acc, D, J) — решение задачи для жестких систем на отрезке с использованием алгоритма Розенброка;
- stiffr(y, x1, x2, acc, D, J, kmax, save) —решения задач для жестких систем на отрезке с использованием алгоритма Розенброка;
- Stiffb(y, x1, x2, acc, D, J) —решение задачи для жестких систем на отрезке с использованием алгоритма Булирша—Штера;
- stiffb(y, x1, x2, acc, D, J, kmax, save) —решение задач для жестких систем в заданной точке с использованием алгоритма Булирша—Штера.
Смысл параметров для всех функций одинаков и определяется математической постановкой задачи:
y — вектор начальных условий 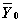
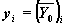
x1, x2 — начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 — начальная точка, x2 — заданная точка;
npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку;
D — имя вектор-функции D(x,y) правых частей 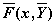
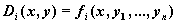
J — имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей: 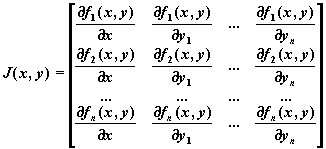
acc — параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение не станет меньше save );
kmax — максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке, максимальное число строк в результате;
save — наименьшее допустимое значение шага неравномерной сетки.
Результат работы функции — матрица, содержащая n+1; ее первый столбец содержит координаты узлов сетки, второй столбец — вычисленные приближенные значения решения y1 (x) в узлах сетки, (k+1) -й — значения решенияyk (x) в узлах сетки.
При решении задачи Коши для дифференциального уравнения первого порядка результат вычислений всех приведенных выше функций — матрица, в первом столбце которой содержатся координаты узлов сетки x0 , x1 , . xN, а во втором — значения приближенного решения в соответствующих узлах.
При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию можно получить рассматривая интегральные и фазовые кривые системы.
При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию о свойствах решений можно получить, построив векторное поле системы.
Запишем автономную систему второго порядка
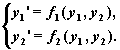
Эта система полностью определяется заданием векторного поля 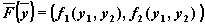
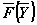
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
http://kafiitbgau.narod.ru/Metod/Mathcad/mathcad-4.htm
http://old.exponenta.ru/soft/Mathcad/learn/ode/ode.asp







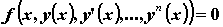 , которое связывает независимую переменную x , искомую функцию y = y ( x ) и ее производные
, которое связывает независимую переменную x , искомую функцию y = y ( x ) и ее производные 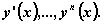
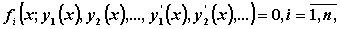 которая связывает независимую переменную x , искомые функции
которая связывает независимую переменную x , искомые функции 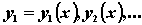 и их производные.
и их производные.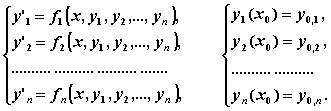
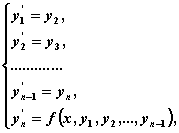
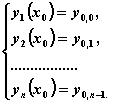
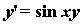 , удовлетворяющее начальным условиям y ( 0)= 1, и построим график найденного решения. Решим задачу численно, используя алгоритм Рунге-Кутты с фиксированным шагом на сетке из 20 равноотстоящих узлов.
, удовлетворяющее начальным условиям y ( 0)= 1, и построим график найденного решения. Решим задачу численно, используя алгоритм Рунге-Кутты с фиксированным шагом на сетке из 20 равноотстоящих узлов. в панели графиков
в панели графиков  и введите в качестве переменной на оси абсцисс Y ( c толбец координат узлов сетки), а на оси ординат — Y (столбец значений решения в узлах сетки). Чтобы ввести номер столбца, введите имя матрицы, щелкните по кнопке
и введите в качестве переменной на оси абсцисс Y ( c толбец координат узлов сетки), а на оси ординат — Y (столбец значений решения в узлах сетки). Чтобы ввести номер столбца, введите имя матрицы, щелкните по кнопке 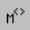 в панели
в панели  и введите в помеченной позиции номер столбца.
и введите в помеченной позиции номер столбца.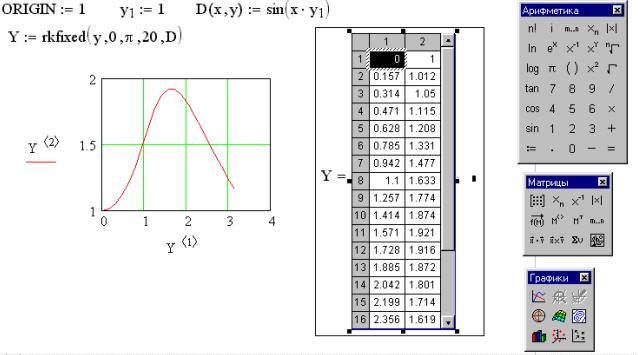
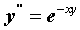 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 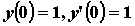 , и построим график найденного решения.
, и построим график найденного решения.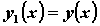 и
и 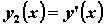 . Поскольку
. Поскольку 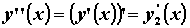 , то получим
, то получим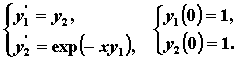
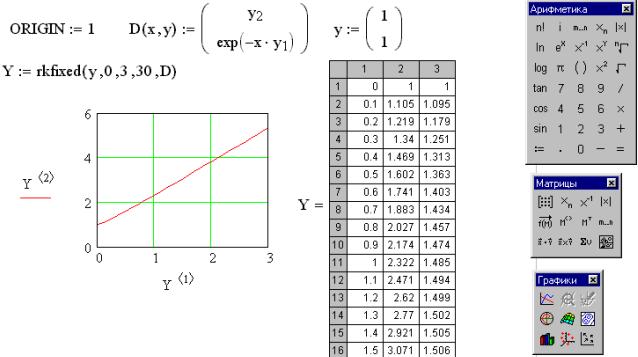
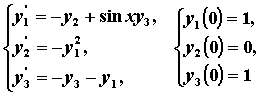
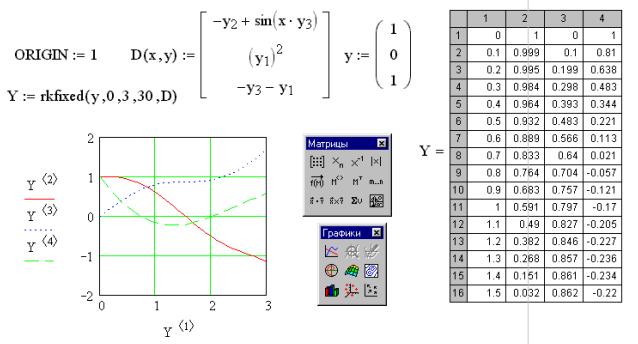
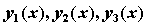 ), введите в качестве переменной на оси абсцисс Y ( c толбец координат узлов сетки), а на оси ординат введите, разделяя запятой, Y , Y , Y (столбцы, содержащие соответственно значения
), введите в качестве переменной на оси абсцисс Y ( c толбец координат узлов сетки), а на оси ординат введите, разделяя запятой, Y , Y , Y (столбцы, содержащие соответственно значения 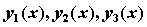 в узлах сетки).
в узлах сетки).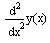 или в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.
или в виде y»(x). При этом необходимо обязательно записывать аргумент искомой функции.