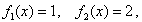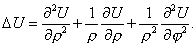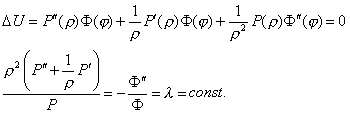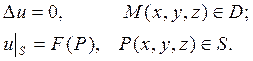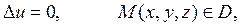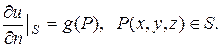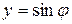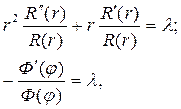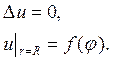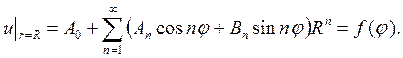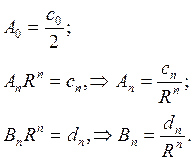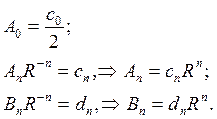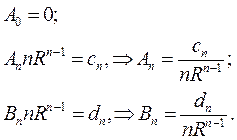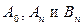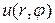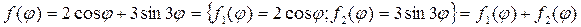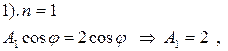Задача неймана для уравнения лапласа вне круга
На этой странице нашего сайта размещены учебно-методические пособия по уравнениям математической физики (классический курс) в форме презентаций, которые использовались при проведении дистанционных занятий со студентами МФТИ в марте-мае 2020 года во время самоизоляции, вызванной коронавирусной инфекцией.
Каждое из учебно-методических пособий содержит теоретические сведения и примеры решения типовых задач по изучаемому разделу уравнений математической физики. Практически все разобранные в учебно-методических пособиях задачи ранее предлагались для решения студентам МФТИ в заданиях для самостоятельной работы и на письменных экзаменационных контрольных работах. В справочной форме приводится необходимая для решения задач теория.
Мы надеемся, что эти учебные материалы будут полезными не только студентам МФТИ, осваивающим классический курс уравнений математической физики, но и студентам других ВУЗов.
Дистанционное занятие на тему «Функция Грина оператора Штурма-Лиувилля»
Дистанционное занятие посвящено решению задач, связанных с построением функции Грина оператора Штурма-Лиувилля.
Содержание
- Оператор Штурма-Лиувилля
- Задача Штурма-Лиувилля
- Построение функции Грина оператора Штурма-Лиувилля
- Сведение задачи Штурма-Лиувилля к интегральному уравнению
- Примеры решения задач
 | Учебно-методическое пособие на тему «Функция Грина оператора Штурма-Лиувилля» |
Дистанционное занятие на тему «Уравнения Лапласа и Пуассона в круговых областях»
Дистанционное занятие посвящено решению задач Дирихле и Неймана в круговых областях на плоскости.
Содержание
- Уравнения Лапласа и Пуассона на плоскости
- Задача Дирихле для уравнений Лапласа и Пуассона в круге
- Задача Дирихле для уравнений Лапласа и Пуассона вне круга
- Задача Дирихле для уравнений Лапласа и Пуассона в кольце
- Задача Неймана для уравнений Лапласа и Пуассона в круге. Необходимое условие разрешимости
- Задача Неймана для уравнений Лапласа и Пуассона вне круга. Необходимое условие разрешимости
- Задача Неймана для уравнений Лапласа и Пуассона в кольце. Необходимое условие разрешимости
- Общий вид гармонических функций в круговых областях
- Примеры решения задач
 | Учебно-методическое пособие на тему «Уравнения Лапласа и Пуассона в круговых областях» |
Дистанционное занятие на тему «Сферические функции»
Дистанционное занятие посвящено решению задач Дирихле и Неймана в сферически симметричных областях в пространстве.
Содержание
- Уравнения Лапласа и Пуассона в пространстве
- Краевые задачи для уравнений Лапласа и Пуассона в сферически симметричных областях в пространстве
- Оператор Лапласа в сферических координатах
- Оператор Лапласа-Бельтрами
- Сферические функции
- Полиномы Лежандра
- Присоединенные полиномы Лежандра
- Общий вид сферических функций
- Общий вид гармонических функций в сферически симметричных областях в пространстве
- Примеры решения задач
 | Учебно-методическое пособие на тему «Сферические функции» |
Дистанционное занятие на тему «Функция Грина задачи Дирихле»
Дистанционное занятие посвящено решению задач на построение методом отражений функций Грина задач Дирихле и решению задачи Дирихле для уравнения Пуассона в пространстве при помощи функции Грина.
Содержание
- Определение функции Грина задачи Дирихле
- Применение функции Грина для решения задачи Дирихле
- Примеры решения задач. Метод отражений
 | Учебно-методическое пособие на тему «Функция Грина задачи Дирихле» |
Дистанционное занятие на тему «Объемный потенциал»
Дистанционное занятие посвящено двум способам вычисления объемного потенциала: по определению и при помощи использования свойств объемного потенциала.
Содержание
- Определение объемного потенциала
- Физический смысл объемного потенциала
- Свойства объемного потенциала
- Пример вычисления объемного потенциала для шара двумя способами: по определению и при помощи использования свойств объемного потенциала
 | Учебно-методическое пособие на тему «Объемный потенциал» |
Дистанционное занятие на тему «Потенциалы простого и двойного слоя»
Дистанционное занятие посвящено двум способам вычисления потенциалов простого и двойного слоя: по определению и при помощи использования свойств потенциалов простого и двойного слоя.
Граничные условия. Задачи Дирихле и Неймана








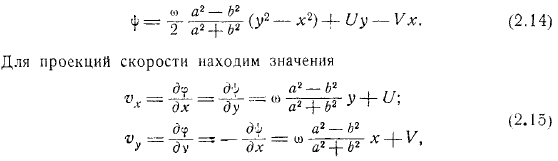

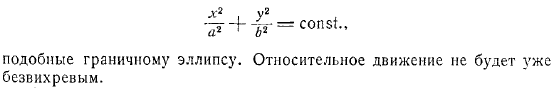
Граничные условия. Задачи Дирихле и Неймана
Поиск комплексного потенциала, определяющего планарное невращательное движение несжимаемой жидкости гидромеханики, можно свести к поиску функции потока, поскольку потенциал связан с известными условиями Коши. Римана, из известной функции можно определить в виде квадратуры. Функция потока, которая считается непрерывной во всех точках течения несжимаемой жидкости, удовлетворяет уравнению Лапласа в этих точках, а на определенных границах течения-некоторым известным условиям. Формат зависит от реализации квартиры.
Показаны простейшие случаи, без цели исчерпывающей классификации различных типов граничных условий. Рассматривая плоское течение бесконечно статичной бесконечной жидкости о движении тела в идеальной жидкости, возникающее при движении цилиндра, граничные условия для функции потока однозначно следующие — поскольку скорость в этих точках должна быть равна нулю. В каждой точке контура движущегося тела, нормальная проекция скорости должны совпадать.
- Угол между элементом линии потока и осью, а соотношение между позволяет выразить рассматриваемое условие. И если в жидкости еще есть неподвижный объект, то по их контуру понятно, что обычная составляющая скорости соседних частиц жидкости должна быть равна нулю, другими словами, сам неподвижный контур должен находиться в контакте с текущей линией. В этом случае необходимо добавить граничное условие к предыдущему условию. Для точки фиксированного контура.
Если тело движется поступательно со скоростью, направленной вдоль оси, то условие равно. Принять форму, или все точки контура, после того как цилиндрический объект совершает какое-либо движение. При наличии поступательного потока с бесконечно большой скоростью расстояние до удаленной точки равно, ориентированной вдоль оси и обтекающей неподвижный объект. Граничное условие, очевидно, выглядит так: для бесконечности показанные нами граничные условия в основном используются при исследовании стационарного движения, но остаются справедливыми для нестационарного потенциала.
В этом случае предыдущее выражение вводит только время в качестве параметра. Параметры зависят от. Известное значение функции на контуре области называется задачей Дирихле, хотя это задача определения функции, удовлетворяющей уравнению Лапласа в области. Таким образом, мы видим, что определение плоского невращательного движения несжимаемой жидкости, вызванного движением контура, ограничивающего область течения, приводит к решению конкретной задачи Дирихле.
При решении гидродинамических задач можно также сначала найти все потенциалы скорости. Он также должен удовлетворять уравнению Лапласа в области течения. Но является ли граничное условие схемы необходимым для функции? Другой само определение потенциала скорости является вертикальной проекцией в скорости частицы жидкости, прилегающие к контуру, и, следовательно, граничное условие для функции принимает форму an является нормальной проекции скорости точки контура. В частности, в терминах фиксированных границ, мы получим условие.
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Людмила Фирмаль
В области, задача определения функции, которая удовлетворяет уравнению Лапласа по известному значению нормальной производной функции на контур области называется задачей Неймана. Поэтому гидродинамические задачи приводят к решению некоторых задач Неймана. Вы можете использовать функцию для определения функции и наоборот. Поэтому ясно, что задача Неймана может быть сведена к задаче Дирихле, или наоборот. Факт, запомните состояние Коши-Римана и проследите за цифрой некоторое время.
Направление нормали в направлении оси, и направление касательной в направлении оси, получаем следующие соотношения сразу, вы можете перейти к задаче Неймана из задачи Дирихле, если есть проблема Неймана, то есть, если вы знаете значение на схеме, это будет следующим образом. Переходим к границе области течения, и поэтому Дирихле. В случае задачи многосвязной области с границей на контуре предыдущее выражение отображает значение аддитивной постоянной для каждой схемы. По значению одной из этих аддитивных констант движение определяется значением производной функции, поэтому его можно выбрать.
Любые константы в будут отображаться. Дана циркуляция скоростей по контуру, которые неприводимы друг к другу. Это полностью совпадает с замечанием о том, что вращательные движения, сделанные в конце раздела главы движение кругового цилиндра , полностью определяются задачей. И цикл только в том случае, если настройка циклическая. В качестве простого примера рассмотрим задачу о невращательном движении несжимаемой жидкости, заключенной в эллиптический цилиндр. Пусть эллиптическое уравнение.
- Его движение характеризуется проекцией на координатную ось скорости и угла поворота скорости его центра. Тогда функция потока должна удовлетворять уравнению в эллипсе и граничному условию самого эллипса. Полином порядка. Я ищу функцию в виде. Уравнение представляет собой отношение. Уравнение из условия является результатом. Это означает связь между для проекции скорости найдите значение, вы можете получить оттуда легко.
Простейший случай чистого поступательного движения цилиндра, когда, выглядит так: то есть жидкость движется вместе со всем цилиндром. Для чистого вращения, когда, это выглядит так: линия потока абсолютного движения гиперболическая. Подчеркнем, что полученная нами формула определяет абсолютное движение жидкости, но относится к движущимся координатным осям.
Движение жидкости относительно этих движущихся координатных осей определяется вычитанием проекции переносной скорости из проекции абсолютной скорости. В результате проекция относительной скорости выглядит следующим образом и представляет собой эллипс, аналогичный граничному эллипсу. Относительное движение больше не является вихревым.
В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Людмила Фирмаль




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Краевые задачи для уравнения лапласа в круговом цилиндре
Краевые задачи для уравнения лапласа в круговом цилиндре
Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.
Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.
Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.
Краевые задачи для уравнения лапласа в круговом цилиндре
3.3. Задача Дирихле для уравнения Лапласа в кольце
Найти функцию U, удовлетворяющую уравнению
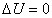 внутри кольца. внутри кольца. | (1) |
Необходимо поставить краевые условия на каждой из границ:
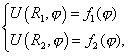 | (2) |
где 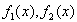

Для простоты вычислений возьмем 
тогда краевые условия примут вид
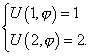 | (2*) |
Запишем уравнение (1) в полярных координатах
Решим уравнение методом разделения переменных, то есть будем искать решение уравнения (1) вида
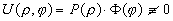
Тогда уравнение (1) примет вид
Отсюда получим два обыкновенных дифференциальных уравнения.
 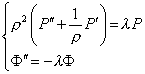 |
Необходимо определить знак 

и при 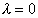
Удовлетворим краевым условиям (2*). Необходимо выяснить, какие из коэффициентов являются лишними.
Решения краевых задач для уравнения Лапласа в круге


Уравнением Лапласа описываются различные физические процессы и в каждой задаче искомое решение должно удовлетворять уравнению в некоторой области D, а также некоторому дополнительному условию на границе S этой области D.
В зависимости от вида граничного условия различают следующие основные виды граничных задач:
1) найти решение уравнения Лапласа, удовлетворяющее граничным условиям первого рода: 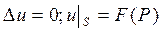
2) найти решение уравнения Лапласа, удовлетворяющее граничным условиям второго рода: 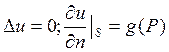
3) найти решение уравнения Лапласа, удовлетворяющее граничным условиям третьего рода: 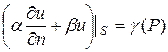
где 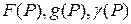
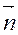
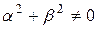
Краевые задачи могут быть внутренними или внешними. Они различаются в зависимости от того, в какой области внутренней или внешней относительно поверхности S ищется решение.
Внутренняя задача Дирихле формулируется следующим образом: Найти непрерывную в замкнутой области 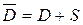
Внутренняя задача Неймана формулируется так: найти внутри области D решение и(М) уравнения Лапласа
непрерывное в замкнутой области 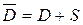
Рассмотрим теперь краевые задачи для уравнения Лапласа внутри круга и вне его. Пусть существует область, представляющая собой круг радиуса R. Запишем двухмерное уравнение Лапласа в полярных координатах, полагая, что 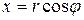
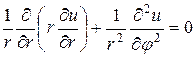
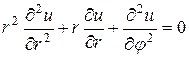
Для нахождения частных решений уравнения (18.12) используем метод Фурье и представим эти решения в виде
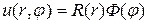
После подстановки решения (18,13), первой и второй производной от этой функции по r, а также второй производной от нее по φ в исходное уравнение (18.12), получим
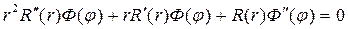
Разделим в этом уравнении переменные
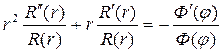
Это равенство выполняется тогда и только тогда, если обе его части равны одной и той же постоянной, например, λ
Тогда для каждой функции 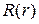
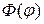
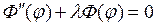
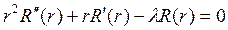
Рассмотрим сначала уравнение (18.15) для функции 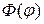
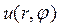
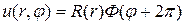
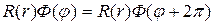
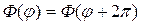
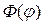
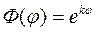
После подстановки которого в уравнение (18.15) получим характеристическое уравнение
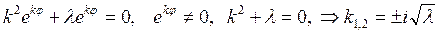
Корни характеристического уравнения являются исключительно мнимыми, поэтому общее решение уравнения (18.15) при 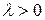
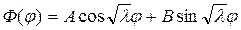
и в силу периодичности функции 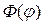
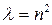
В самом деле, из равенства
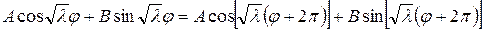
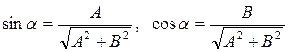
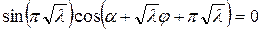
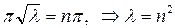
Следовательно, частные решения уравнения (18.15) при различных значениях n можно записать в виде
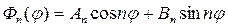
Исходя из (18.18) следует, что уравнение (18.16) можно записать в виде
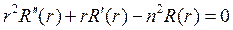
Уравнение (18.20) в случае, когда 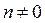
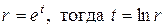
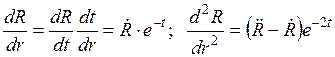
Следовательно, подставив эти производные в уравнение (18.19) получим обыкновенное линейное и однородное дифференциальное уравнение с постоянными коэффициентами
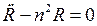
Решение этого уравнения будем искать в виде
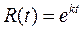
Вычислим от этой функции производные и подставим в уравнение (18.21)
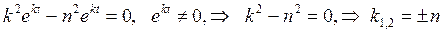
следовательно общее решение уравнения (18.21) имеет вид
и возвращаясь к переменной r, получим
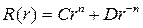
Если в уравнении (18.20) 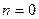
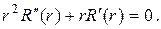
Это уравнение также является уравнением Эйлера, поэтому, производя замену 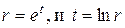
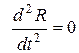
решение которого будет иметь вид
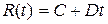
и возвращаясь к переменной r, получим
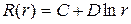
решение уравнения (18.20) при 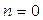
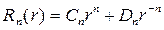
Подставляя (18.19) и (18.25) в решение (18.13) получим набор частных решений
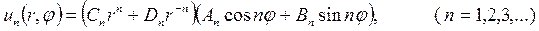
используя принцип суперпозиции, а также вследствие линейности и однородности уравнения Лапласа можно утверждать, что сумма частных решений также будет его решением, следовательно, общее решение уравнения Лапласа будет иметь вид
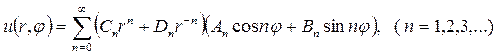
Пользуясь этой формулой и задавая граничные условия первого, второго и третьего рода можно решать как внутренние, таки внешние граничные задачи – Дирихле, Неймана и смешанную задачу.
I.Рассмотрим внутреннюю задачу Дирихле для уравнения Лапласа в круге радиуса R
Для решения этой задачи используем формулу (18.26), учитывая при этом, что функция 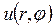
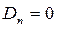
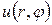
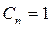
получим решение уравнения Лапласа
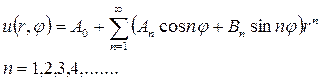
Удовлетворим в этом решении поставленным граничным условиям
Разложим функцию f(φ) в ряд Фурье на интервале от 0 до 2π
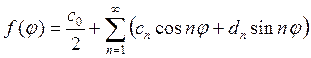
следовательно, можно записать
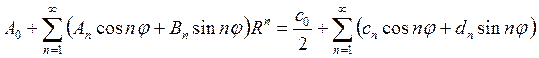
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
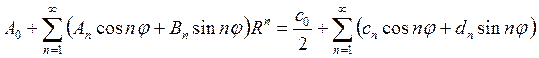
найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.27), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
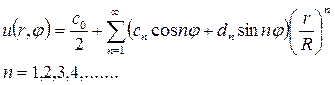
где cn и dn коэффициенты, заданные поставленными граничными условиями.
Решение задачи Дирихле также можно получить и используя формулу Пуассона
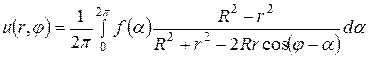
которая при непрерывной функции 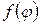
II.Рассмотрим внешнюю задачу Дирихле для уравнения Лапласа в круге радиуса R
Для решения этой задачи используем формулу (18.26), учитывая при этом, что функция 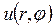
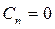
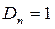
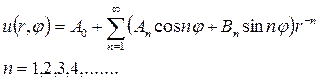
Удовлетворим в этом решении поставленным граничным условиям
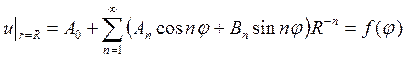
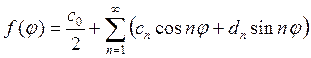
Следовательно, можно записать
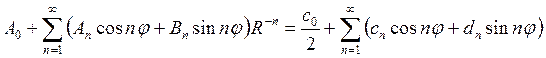
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
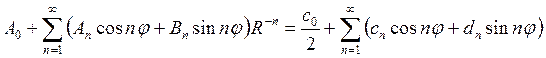
найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.30), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
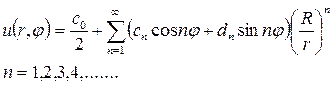
где cn и dn коэффициенты, заданные поставленными граничными условиями.
III.Рассмотрим внутреннюю задачу Неймана:
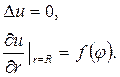
Для решения этой задачи вычислим производную от решения (18.27)
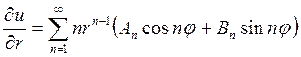
И запишем граничные условия
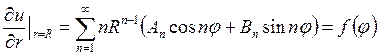
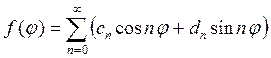
Следовательно, можно записать
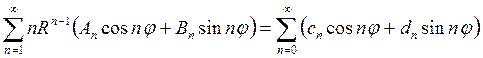
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства, найдем значения искомых коэффициентов An и Bn
Подставляя найденные коэффициенты в решение (18.33), получим окончательное решение внутренней задачи Неймана для уравнения Лапласа в круге
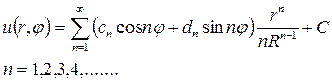
где С – произвольная постоянная.
Необходимо отметить, что решение задачи Неймана существует только при условии
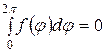
и определяется с точностью до произвольной постоянной.
Смешанная граничная задача для уравнения Лапласа в круге радиуса R решается аналогично задачам рассмотренным выше.
Пример 18.1. Найти решение уравнения Лапласа для внутренней части круга радиуса R, удовлетворяющее краевому условию
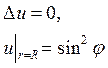
▲ Здесь задана задача Дирихле, где правая часть граничного условия (П18.1.1) 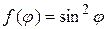
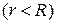
Для этого подставим само решение (18.28) в левую часть граничного условия (П18.1.1) при 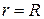
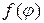
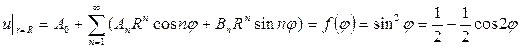
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами и при свободном члене в левой и правой частях полученного равенства (П18.1.2)
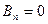
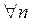
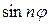
а также все остальные 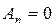
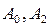
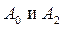
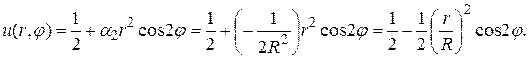
Пример 18.2. Найти решение уравнения Лапласа внутри круга радиуса R 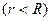
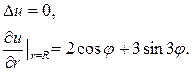
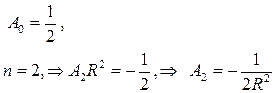
▲ Здесь задана задача Неймана, где правая часть граничного условия (П18.2.1) 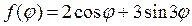
и для каждой из них найдем решение. Прежде чем решать поставленную задачу проверим выполнение условия (18.32)
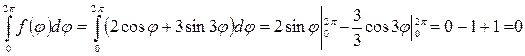
так как условие (18.32) выполнено, то для решения поставленной задачи воспользуемся, описанном выше алгоритмом (III.)
Вычислим производную от решения (18.27)
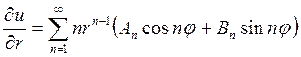
и запишем граничные условия сначала для функции
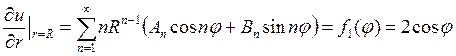
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.2):
а все остальные 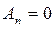
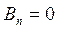
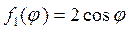
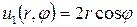
Затем запишем граничные условия сначала для функции
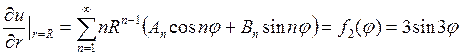
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.3):
а все остальные 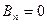
Следовательно, решение, соответствующее функции 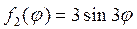
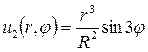
Таким образом, решение исходной задачи будет определяться формулой
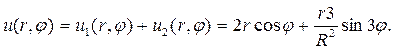
http://lfirmal.com/granichnye-usloviya-zadachi-dirihle-i-nejmana/
http://medwegonok.ru/kraevye-zadachi-dlya-uravneniya-laplasa-v-krugovom-tsilindre/