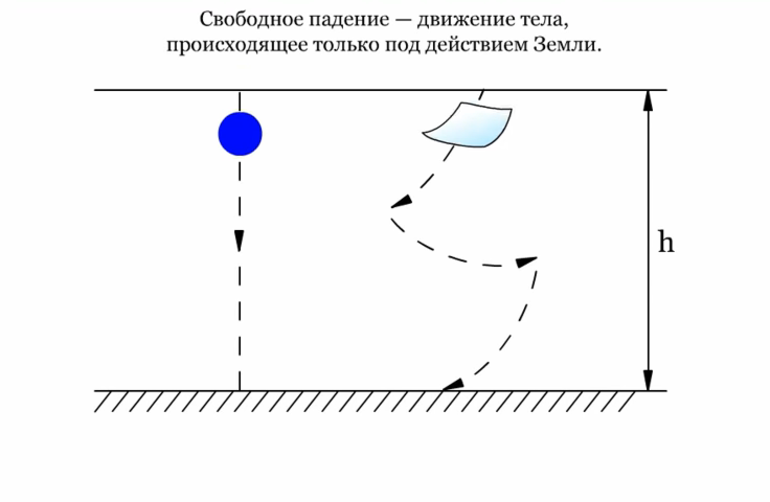
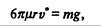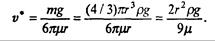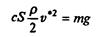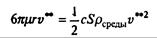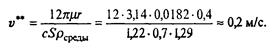СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение Fcoпp = k1v, где k1 определяется свойствами среды и формой тела. Например, для шарика k1 = 6πμr — это формула Стокса, где μ -динамическая вязкость среды, r — радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм.μ = 0,0182 Н∙с∙м -2 , для воды 1,002 Н∙с∙м -2 , для глицерина 1480 Н∙с∙м -2 .
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
Пусть r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). При падении в воздухе v* ≈ 960 м/с, в воде v*≈ 17 м/с, в глицерине v* ≈ 0,012 м/с.
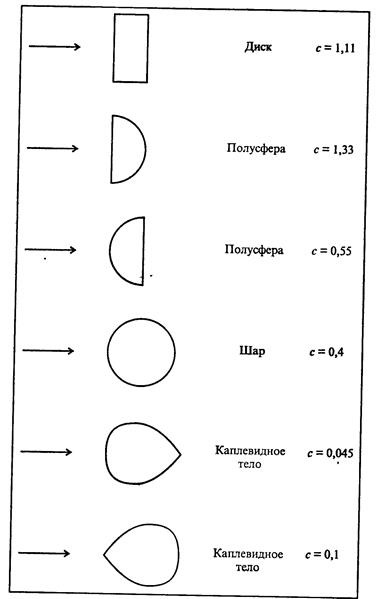
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: Fcoпp = k2v 2 . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если k2v 2 >> k1v, то вкладом k1v можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды ρсреды и зависит от формы тела. Обычно представляют k2 = 0,5сSρсрeды, где с — коэффициент лобового сопротивления — безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис. 7.6.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичнойзависимости силысопротивления от скорости.
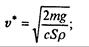
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
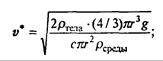
Примем r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). Тогда для движения в воздухе (ρвозд= 1,29 кг/м 3 ) получаем v* ≈ 18 м/с, в воде (ρводы ≈ 1∙10 3 кг/м 3 ) v* ≈ 0,65 м/с, в глицерине (ρглицерина = 1,26∙10 3 кг/м 3 ) v* ≈ 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения — уравнение второго закона Ньютона с учетом двух сил, действующих на тело; силы тяжести и силы сопротивления среды:
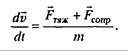
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
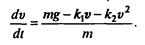
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7.7), заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, dv/dt = 0, и соответствующую установившуюся скорость 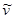
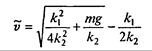
(второй — отрицательный — корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от v0 до 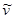
Однако, даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. II хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны (один из лучших помощников в их поиске — справочник Камке). Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций — а как найти закон изменения во времени перемещения? — Формальный ответ прост:
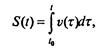
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно стандартна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т.е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых, специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс -а именно это есть цель моделирования.
В достижении этой цели компьютер — незаменимый помощник. Независимо от того, какой будет процедура получения решения — аналитической или численной, -задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения v и S, найденные компьютером, следует записывать в результирующую таблицу (табл. 7.2).
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
| t(c) | s(m) | v (м/с) | t(с) | S(м) | v (м/с) |
| 0 | 200,1 | 35,6 | |||
| 4,8 | 9,6 | 235,9 | 36,0 | ||
| 18,7 | 17,9 | 272,1 | 36,3 | ||
| 40,1 | 24,4 | 308,5 | 36,4 | ||
| 66,9 | 28,9 | 345,0 | 36,5 | ||
| 97,4 | 31,9 | 381,5 | 36,6 | ||
| 130,3 | 33,8 | 418.1 | 36,6 | ||
| 164,7 | 35,0 | 454,7 | 36,6 |
Кроме таблицы необходимы графики зависимостей v(t) и S(t); по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественноепонимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске — приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом — скажем, через каждый метр или каждые 100 метров — смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений
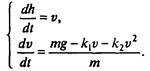
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно — будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он — опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не «солдатиком», а лицом вниз, «лежа», раскинув руки в стороны. Рост человека возьмем средний — 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния — это приблизительно 0,4 м. Для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с = 1,2 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь: S = 1,7∙0,4=0,7 (м 2 ).
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость v**. Тогда
Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге — Кутта, одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. — эти сугубо математические проблемы здесь не обсуждаются. Программа, реализующая метод Рунге — Кутта четвертого порядка, может быть взята из примера, приведенного в следующем параграфе или из какого-нибудь стандартного пакета математических программ.
Отметим, что существует немало программ, моделирующих простые физические процессы типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как сугубо иллюстративные.
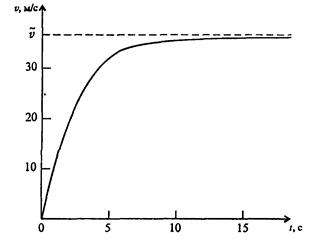
Вычисления производились до тех пор, пока «безпарашютист» не опустилсянаводу. Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до приземления (рис. 7.7). Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости, изображенный на рисунке, заменился бы касательной к нему в начале координат.
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
В некоторых случаях для ускорения процесса работы над какой-либо задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором). Покажем это на примере рассматриваемой задачи. В табл. 7.3 представлен небольшой фрагмент из табличного процессора Excel. Решение находится с помощью, так называемого, исправленного метода Эйлера — одного из возможных вариантов метода Рунге — Кутта второго порядка.
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага вычислений, массы «безпарашютиста», величины mg. Это связано с тем, что все константы также удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы. Достаточно записать
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
| А | В |
| t | v |
| 0 | |
| =СУММ(АЗ; D2) | =B3+D2/2* ( (D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4) |
| =СУММ(А4; D2) | =B4+D2/2* ( (D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4) |
| =СУММ(А5; D2) | =B5+D2/2*( (D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4) |
| =СУМM(А6; D2) | =B6+D2/2* ( (D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4) |
| =СУММ(А7; D2) | =B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4) |
формулу правильно один раз, а затем скопировать в остальные ячейки, при этом, как известно, она «настраивается» на соответствующую ячейку.
Свободное падение тел — формулы, законы и задачи
Общие сведения
Основоположником создания учения о движении стал Аристотель. Он утверждал, что скорость падения тела зависит от его веса. Значит, тяжёлый предмет сможет долететь до Земли быстрее, чем лёгкий. Если же на объект не будут воздействовать какие-либо силы, его движение невозможно.
Но Галилео Галилей, известный итальянский изобретатель и физик, изучая падение различных предметов и их инерцию, смог опровергнуть догадки Аристотеля. Результаты его исследований были революционными в науке. При этом даже была выпущена книга «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению», в которой были изложены основные размышления Галилея.
За дату рождения кинематики как науки можно принять 20 января 1700 года. В это время проходило заседание Академии наук, на котором Пьер Вариньона не только дал определения понятиям скорость, ускорение, но и описал их в дифференциальном виде. Уже после Ампер использовал для изучения процессов вариационное исчисление. Наглядные опыты провёл Лейбниц, а потом. профессор МГУ Н. А. Любимов смог продемонстрировать появление невесомости при свободном падении.
Под невесомостью понимают состояние тела, при котором силы взаимодействия с опорой, существующие из-за гравитационного притяжения, не оказывают никакого влияния. Такое положение имеет место, когда воздействующие на тело внешние силы можно охарактеризовать массовостью, например, тяготения.
В этом случае силы поля сообщают всем частицам предмета в любом из его положений равные по модулю и направлению ускорения, либо при движении возникают одинаковые по модулю скорости всех частиц тела. Например, поступательное движение. Состояние невесомости особо ярко проявляется в начальный момент при падении тела в атмосфере. Это связано с тем, что сопротивление воздуха ещё невелико.
Таким образом, для существования свободного падения нужно выполнение как минимум двух условий:
- малость или отсутствие сопротивления среды;
- действие лишь одной силы тяжести.
Что интересно, движение вверх тоже считается свободным падением, несмотря на обратное интуитивное восприятие, поэтому траектория движения может иметь форму как участка параболы, так и отрезка прямой. Например, камень, брошенный с небольшой высоты или поверхности под любым углом.
Опыт Галилея
Падение относится к реальному движению. Любое взаимодействие с Землёй приводит к изменению скорости из-за чего возникает ускорение. В 1553 году итальянец Джованни Бенедетти заявил, что 2 тела с разной массой, но одинаковой формы, брошенные в одной среде за одинаковое время пролетят равные расстояния. Это утверждение нуждалось в доказательстве, так как противоречило общепринятому на тот момент времени пониманию процессов. В частности, высказываниям Аристотеля.
Одним из экспериментаторов стал Галилей. Для проведения опыта учёному понадобилось:
- стофунтовое ядро;
- однофунтовый шар.
Существует мнение, что вместо шара учёный использовал мушкетную пулю. Эксперимент заключался в следующем. Подняв 2 предмета на Пизанскую башню, Галилей сбросил их одновременно. Наблюдающие люди воочию смогли убедиться, что 2 тела упали на землю одновременно. Когда же один из учеников Аристотеля упрекнул итальянца, что на такой малой высоте невозможно оценить достоверно разницу, экспериментатор ответил: «Проделайте опыт самостоятельно, вы найдёте, что более тяжёлый предмет опередит тот, что легче на 2 пальца, поэтому, когда первый упадёт на землю, то второй будет от него на расстоянии толщины двух пальцев».
В своих работах Галилей рассуждал, что если связать верёвкой 2 тела разной тяжести, то с большим весом, по мнению Аристотеля, предмет будет лететь быстрее. Причём лёгкий объект начнёт замедлять падение тяжёлого. Но так как система в целом тяжелее, чем отдельно взятые тела, падать она должна быстрее самого тяжёлого тела. Другими словами, возникает противоречие, значит, предположение о влиянии веса на скорость падения неверно.
Сегодня эксперимент, подтверждающий доводы Галилея, может провести самостоятельно, пожалуй, каждый интересующийся. Такой опыт часто демонстрируют в средних классах общеобразовательной школы. Для этого нужно взять 2 трубки, длиной более метра и поместить в них 2 шарика разной массы. Затем создать внутри вакуум и одновременно их перевернуть. Если все условия соблюдены верно, то 2 тела опустятся на дно ёмкостей одновременно.
Если же опыт повторить не в вакууме, на шары будет действовать сила сопротивления, поэтому время падения уже не будет совпадать. Причём зависеть оно будет от формы предмета и его плотности.
Закон ускорения
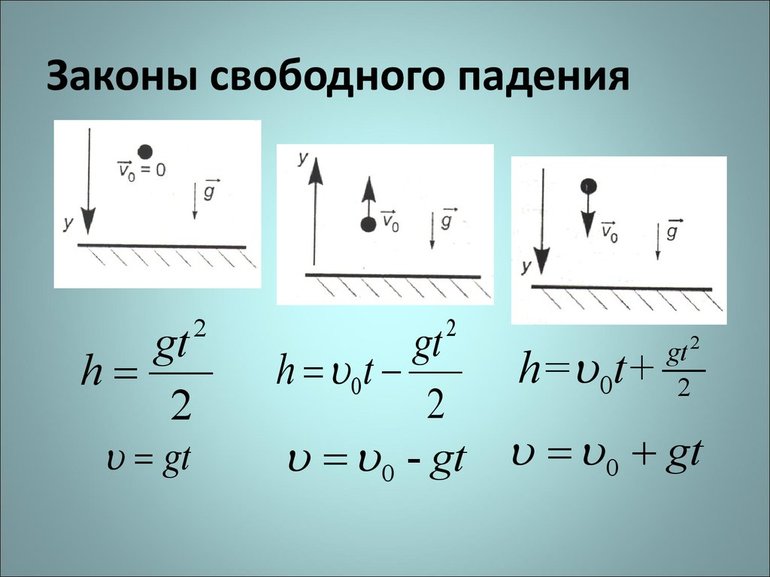
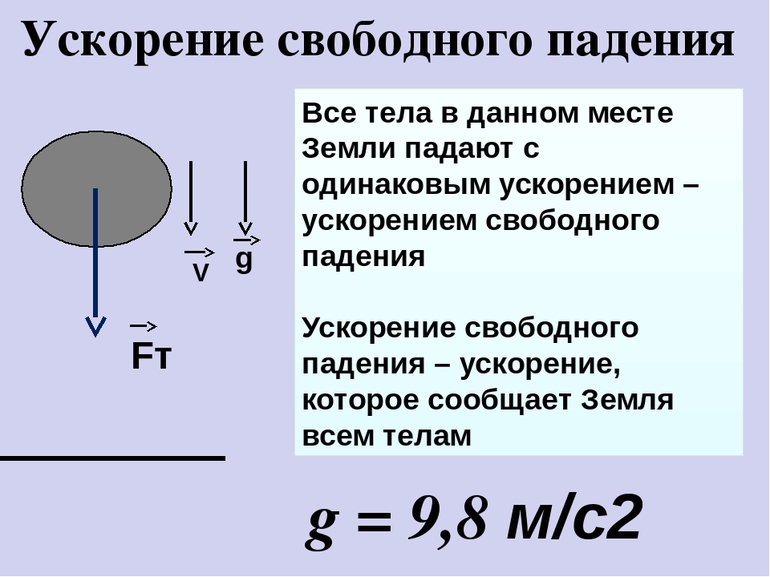
Формула для свободного падения была выведена из выражения, определяющего силу тяжести: F = m * g. В соответствии с законом, падение предметов выполняется с одним и тем же ускорением вне зависимости от массы тела. По сути, это частный случай равноускоренного движения, обусловленное силой тяжести.
Для количественного анализа нужно ввести систему координат, взяв начало у поверхности Земли. Тогда можно рассмотреть падение тела массой m с высоты y0. Причём вращением планеты и сопротивлением воздушной среды нужно пренебречь.
Дифференциальное уравнение будет иметь вид: my = — mg, где: g — ускорение свободного падения. Само же дифференцирование выполняется по времени. При заданных начальных условиях y = y0 и беря во внимание проекцию скорости на вертикальную ось после интегрирования, зависимость переменных от t примет вид:
- v = v0 + gt;
- y = y0 + v0t — (gt 2 / 2).
Из полученных формул становится понятно, почему свободное падение не зависит от массы тела. При этом если начальная скорость будет равна нулю, то есть при падении предмету не сообщается импульс, текущее движение пропорционально времени, а пройденный путь определяется его квадратом.
Как показали эксперименты, если сопротивления воздуха нет, ускорение для любых летящих предметов по отношению к Земле составит 9,8 м / с 2 . Формулы, которые используются при расчёте величин, совпадают с выражениями, справедливыми для любого равноускоренного движения. Например, если тело падает без начальной скорости, его скорость можно найти по формуле: V 2 = g * t, а высоту падения определить так: h = (gt 2 / 2).
Следует отметить, что при удалении предмета от Земли значение свободного движения уменьшается. Причём из-за формы планеты на экваторе оно будет составлять 9,78 м / с 2 , а с противоположной стороны — 9,832 м / с 2 . Чтобы определить значение в любом месте, используют нитяной маятник. Его период колебаний определяется по формуле: T = 2p√(l / g), где l — длина нити.
Значения силы тяжести также зависит от строения земной коры и содержащихся в недрах полезных ископаемых. С учётом этого рассчитываются гравитационные аномалии: Δg = g — gср. Например, если g > gcp, то с большой вероятностью в земле содержатся залежи железной руды, в ином случае — нефти или газа.
Решение задач
Свободно двигаться, то есть не испытывать действие сторонних сил, могут любые тела в вакууме. Но в реальности на них оказывается воздействие как атмосферными явлениями, так и сопротивлением среды. При решении задач учитывается только сила тяжести, а вот остальными явлениями пренебрегают, считая их ничтожно малыми.
Вот некоторые из типовых задач, используемые при обучении в среднеобразовательных школах:
- Деревянная бочка падает с 30 метров. Какова будет её скорость перед столкновением с Землёй? Так как рассматривается свободное падение, для решения нужно использовать формулу: v 2 = 2 * g * h. Отсюда, v = √(2 * g * h) = (2 * 9,81 м / с 2 * 30 м) = 24,26 м/с.
Тело вылетает вертикально вверх со скоростью 45 м/с. Какой высоты оно достигнет перед изменением направления полёта и сколько для этого понадобится времени. Для начала следует записать формулу скорости: v = v0 — gt. Отсюда можно рассчитать время полёта: t = v0 / g = 45 / 9,8 = 4,6 c. Теперь можно определить максимальную высоту: h = vot — (gt 2 / 2) = 45 м / с * 4,6 с — 9,8 м / с 2 * (4,6 c) 2 / 2 = 207 м — 103,7 м = 103,3 м.
Камень летит со скоростью 30 м/с. Найти время, за которое он достигнет 25 метров. Система уравнений, описывающая движение, будет выглядеть так: h = v0t — (gt 2 / 2); 25 = 30t — 5t 2 . Полученные уравнения в системе называются квадратными, поэтому нужно выразить одно из другого и определить корни: t 2 — 6t + 5 = 0. В результате должно получиться время, равное одной секунде.
Рассмотренные задания довольно простые. Но есть и повышенной сложности, требующие не только знания формул, но и умения выполнять анализ. Вот одно из таких.
Мяч бросили с горки под углом к горизонту. Через время, равное t = 0,5 c он достигнет наибольшей высоты, а t2 = 2,5 он упадёт. Определить высоту горки, ускорение падения принять равное g = 10 м / с 2 . Скорость движущегося предмета можно представить в координатной плоскости x и y. В горизонтальном направлении сил, оказывающих воздействие, нет. Движение равномерное. Наибольшая высота будет достигнута при h = H + v0y * t1 — (gt 2 1 / 2).
Вертикальную составляющую можно вычислить, руководствуясь геометрическими принципами: v0y = v0 * sin (a). Учитывая, что h = (gt 2 / 2), для высоты горки можно записать: H = (g * (t 2 1 + t 2 2) / 2) — t1 * v0 sin (a). Так как gt1 = v0 sin (a), то рабочая формула примет вид: H = (g * (t 2 1 + t 2 2) / 2) — gt 2 1. После подстановки данных в ответе должна получиться высота равная 30 метров. Задача решена.
Scilab в свободном падении
На днях с удивлением обнаружил, что на Хабре почти нет статей по Scilab. Между тем это достаточно мощная система компьютерной математики, открытая и кроссплатформенная, покрывающая широкий спектр инженерных и научных задач. В ряде ВУЗов (к примеру, УрФУ, ИТМО) ее используют для обучения студентов. Одной из самых насущных инженерных задач является решение дифференциальных уравнений (далее — ДУ). В данной статье я покажу как при помощи Scilab решать системы обыкновенных ДУ на примере моделирования знаменитого стратосферного прыжка Феликса Баумгартнера.
Как известно, свободное падение — это равнопеременное движение под действием силы тяжести, когда другие силы, действующие на тело отсутствуют или пренебрежимо малы. В быту часто свободным падением также называют движение в атмосфере Земли, когда на ускорение тела не влияют никакие силы, кроме силы сопротивления воздуха и силы тяжести. Именно таким расширенным пониманием мы и будем пользоваться в дальнейшем.
Задача
Составить диф.уравнения (ДУ), описывающие существенные свойства полета Баумгартнера, решить их средствами Scilab и получить в явном виде зависимости дистанции и скорости от времени свободного падения.
Исходные данные
Т.к. основная задача статьи — все-таки показать, как Scilab умеет решать ОДУ, а не получить идеально точную модель, увлекаться анализом экспериментальных данных (телеметрии), погрешностей и подгонкой мы особенно не будем. Однако для проверки адекватности модели несколько значений все же необходимо взять. Итак:
- Высота прыжка — 39000м.
- Дистанция свободного падения — 36402.6м.
- Время свободного падения — 4 мин 20 сек.
- За первые 20сек Баумгартнер набрал скорость 194 м/сек, через 50сек падения (на высоте 8447м) он развил рекордную скорость в 377м/сек, а к моменту раскрытия парашюта (т.е. через 260 сек полета) скорость падения снизилась до 77 м/сек.
Модель-1 (без учета сопротивления воздуха)
Начнем с простейшей модели, в которой есть только одна сила — сила притяжения Земли. Полагаем, что падение идет строго вертикально, начало координат размещено в точке начала прыжка, ось-y направлена вниз.
Ускорение экстремала, соответственно, равно ускорению свободного падения.
При этом по определению скорости:
Получили систему из двух обыкновенных ДУ. Решаем.
Воспользуемся функцией ode(), входящей в стандартный дистрибутив Scilab-а.
Согласно документации, ode решает явные обыкновенные дифференциальные уравнения, определенные как:
Прямо как в нашем случае. Слева должны быть производные 1го порядка.
Если же ДУ содержит производную 2го, 3го и пр. порядков, то нужно ввести замену(ы) и преобразовать одно уравнение с систему нескольких. Как мы на самом деле и сделали. Ведь ускорение — это 2я производная координаты по времени, от которой мы перешли к 1й производной, введя замену — переменную «скорость» равную dy/dt. Т.е.
от перешли к
Наконец-то переходим к коду (ссылка на github). Его можно писать в предлагаемом средой редакторе SciNotes, равно как и в любом другом текстовом редакторе. Можно также запустить оболочку без графики и вводить команды в консоли. На мой взгляд SciNotes удобнее подсветкой кода и интеграцией в среду разработки.
Первым делом нам нужно описать ДУ в виде функции на языке Scilab.
Затем задаем начальные условия.
После чего вызываем функцию-решатель ode(), передав ей на вход все созданное выше.
В матрице result в итоге окажуться значения искомых функций-решений данной системы ДУ, соответствующие точкам оси времени из указанного в t диапазона.
Посмотрим на то, что получилось в графической форме, а заодно выведем в консоль пару контрольных точек.
Получилась ожидаемая квадратичная зависимость координаты от времени.
Сверимся с практикой:
Cкорость через 50сек = 1762 км/ч (а должно быть 1357 км/ч).
Пройденный путь за 4мин.20сек = 331.3 км (а должно быть 36.4 км.).
Если со скоростью на начальном этапе прыжка, поморщившись, еще можно смириться, то итоговое пройденное расстояние превышено на порядок. Это объясняется тем, что неучтенное нами сопротивление воздуха на начальном участке полета действительно мало из-за разряженности стратосферы и наша простейшая модель худо-бедно справляется, но по мере снижения плотность атмосферы заметно увеличивается, ощутимо падает скорость падения и практика начинает категорически расходиться с теорией.
Если построить более подробный график, на который нанести также экспериментальные точки, то усугубляющееся со временем несоответствие данной модели и реальности станет еще более наглядным. В частности, скорость линейно возрастает, тогда как на практике она должна с определенного момента начать снижаться.
Исправим ситуацию, введя в модель силу сопротивления воздуха.
Модель-2 (с учетом сопротивления воздуха)
Атмосфера будет действовать на летящего с силой
где
с — коэффициент сопротивления
S — наибольшая площадь сечения, перпендикулярного направлению полета
density — плотность воздуха
v — скорость движения
Формула взята отсюда, где также можно почитать аналитическое решение
Нас интересует ускорение (хотя лучше было бы сказать замедление), которое Fair будет сообщать летящему вниз экстремалу, чтобы добавить поправку в первое уравнение системы.
По 2му закону Ньютона
С учетом данной поправки наша система примет вид
Решаем аналогичным образом. Описываем систему ДУ как Scilab-функцию.
Поскольку плотность атмосферы изменяется в зависимости от высоты, нам потребуется написать соответствующую функцию. Таблицу можно взять отсюда. А вообще есть ГОСТ 4401-81 Атмосфера стандартная. Параметры (с Изменением N 1).
Задаем начальные условия и решаем.
Построим график и посмотрим, что получилось.
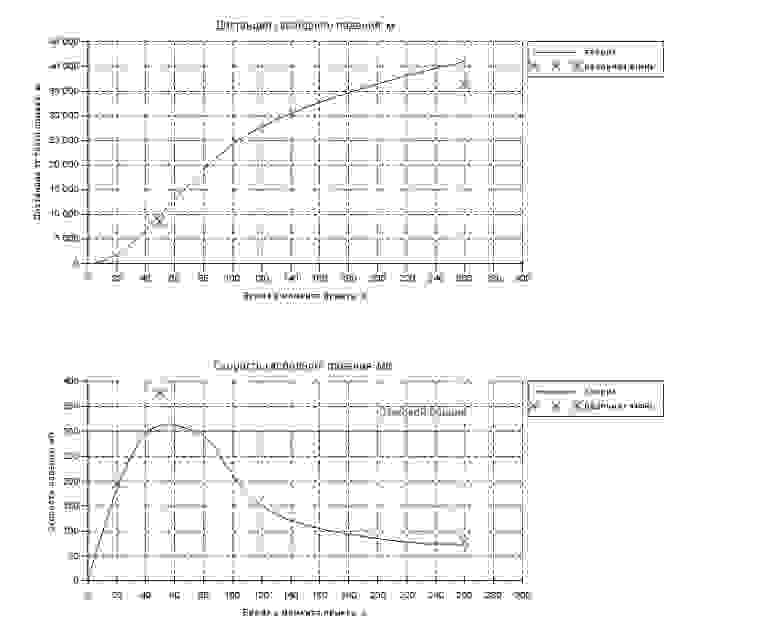
Видим, что между 40-й и 70-й секундами пробьем звуковой барьер, в районе 50й секунды скорость достигнет максимума, после чего начнет снижаться. Набранной скорости не хватит, чтобы сгореть в атмосфере (на Хабре обсуждалось), кроме того к концу полета скорость снизится до величины, позволяющей безопасно открыть парашют. Что соответствует реальности.
Скорость — сравнение теории с экспериментом в контрольных точках
| Время св.падения, с | Расчетная скорость, м/с | Фактическая скорость, м/с |
|---|---|---|
| 20 | 183 | 194 |
| 50 | 312 | 377 |
| 260 | 73 | 77 |
Дистанция св.падения — сравнение теории с экспериментом в контрольных точках
| Время св.падения, с | Расчетная дистанция, м | Фактическая дистанция, м |
|---|---|---|
| 50 | 9853 | 8447 |
| 260 | 41049 | 36403 |
По скорости ошибка в среднем 27 м/с (7% от фактического рекорда), по дистанции свободного падения 3026 м (8% от фактически пройденной в св.падении дистанции). Для наших учебно-демонстрационных целей вполне приемлемо.
Заключение
Таким образом, мы на примере простой, но наглядной, мат. модели рассмотрели как при помощи Scilab решать ДУ, интерполировать, строить графики. Надеюсь эта статься будет полезна начинающим изучать Scilab, а кого-то быть может и подвигнет на дальнейшее применение Scilab в своей практической деятельности.
http://nauka.club/fizika/svobodnoe-padenie-tel.html
http://habr.com/ru/post/327142/