Задачи на каноническое уравнение плоскости

4.2.10. Примеры решения задач по теме «Уравнение плоскости в пространстве»

Составить уравнение плоскости, проходящей через точки А=<5; -1; 3>,

Для того, чтобы составить уравнение плоскости, нужно знать координаты

Точки, лежащей в этой плоскости, и координаты нормали, то есть вектора, перпендикулярного плоскости.

Векторы АВ = (-3; 3; -3) и АС = (-6; 2; -2) параллельны данной плоскости, поэтому их векторное произведение или любой вектор, коллинеарный ему, является нормалью к плоскости.

Выберем в качестве нормали П = (0; 1; 1), а точкой <Х0; У0; Z0> будем считать точку В. Тогда уравнение плоскости имеет вид:

Составить канонические уравнения прямой

Для того, чтобы составить канонические или параметрические уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты направляющего вектора, то есть вектора, коллинеарного прямой.

Прямая является линией пересечения двух плоскостей, поэтому ее направляющий вектор А параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям П1 и П2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [N1, N2].

Будем искать точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить единственным образом из системы уравнений, задающей пересекающиеся плоскости. Выберем для удобства вычислений Z0 = 0, тогда для точки М=<Х0; У0; 0>

Теперь составим канонические уравнения данной прямой:

Ответ:

Составить уравнение плоскости, проходящей через прямую L:

Точка А= <-3,5,-1>принадлежит плоскости, соответственно вектор параллелен плоскости. Кроме того, поскольку данная прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. Следовательно, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Поскольку прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. При T = 0 из уравнений прямой получаем:

Координаты точки А, принадлежащей прямой и соОтВетственно плоскости.

Тогда вектор АМ = (5; -8; 2) параллелен Плоскости. Следовательно, нормаль

П к плоскости коллинеарна векторному произведению [A, AM] = (-6; -9; — 21).

Выберем N = (2; 3; 7) и составим уравнение плоскости, проходящей через

Найти кратчайшее расстояние между прямыми

Координаты направляющих векторов данных прямых A1 = <3; 2; -2>и

A2 = <1; 1; 4>не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составьте уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости; если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A.

Координаты направляющих векторов данных прямых A1 = <3; 2; -2>и

A2 = <1; 1; 4>не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составим уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости (рис.9); если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A (рис.10).

[A1, A2] = (10; -14; 1) = N, точка А= <5; 0; -25>лежит на прямой L1, следова-тельно, она лежит и в плоскости A. Тогда уравнение плоскости A имеет вид:

Точка В= <1; 2; 13>принадлежит прямой L2. Проверим, лежит ли эта точка в плоскости A:

Тогда искомой величиной будет расстояние от В до A. Его можно найти, составив нормальное уравнение плоскости A:

Ответ: .

Найти точку, симметричную точке А(5; -10; 4) относительно плоскости

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ.

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ. Составим уравнения прямой АВ. Эта прямая перпендикулярна A, поэтому ее направляющим вектором можно считать нормаль к плоскости A: A = N = (1; -3; 1).

Параметрические уравнения прямой АВ имеют вид:

Точка О принадлежит и прямой АВ, и плоскости A, поэтому ее координаты должны удовлетворять и уравнениям прямой, и уравнению плоскости. Подставим в уравнение плоскости A параметрические выражения для X, Y, Z из уравнений прямой АВ:

T + 5 – 3(-3T – 10) + T + 4 – 6 = 0; 11T + 33 = 0; T = -3.

Итак, координаты точки О:

Поскольку точка О – середина отрезка АВ, то

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

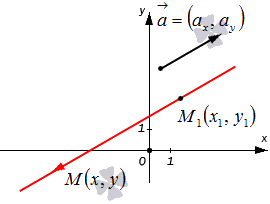
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M 1 ( x 1 , y 1 ) , а также ее направляющего вектора a → = ( a x , a y ) . Попробуем составить уравнение, которое описывало бы эту прямую.

Возьмем плавающую точку M ( x , y ) . Тогда вектор M 1 M → можно считать направляющим для исходной прямой. Его координаты будут равны x — x 1 , y — y 1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).

Множество произвольно взятых точек M ( x , y ) будут определять нужную нам прямую с направляющим вектором a → = ( a x , a y ) только в одном случае – если векторы M 1 M → и a → = ( a x , a y ) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

M 1 M → = λ · a → , λ ∈ R

Если преобразовать полученное равенство в координатную форму, то мы получим:

x — x 1 = λ · a x y — y 1 = λ · a y

При условии, что a x ≠ 0 и a y ≠ 0 , получим:

x — x 1 = λ · a x y — y 1 = λ · a y ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x — x 1 a x = y — y 1 a y также называют уравнением прямой в каноническом виде.

Таким образом, с помощью уравнения x — x 1 a x = y — y 1 a y можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a → = ( a x , a y ) и проходит через точку M 1 ( x 1 , y 1 ) .

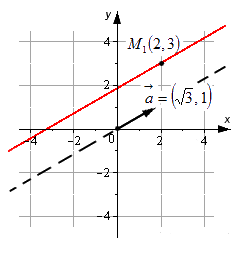
Примером уравнения подобного типа является, например, x — 2 3 = y — 3 1 . Прямая, которая задана с его помощью, проходит через M 1 ( 2 , 3 ) и имеет направляющий вектор a → = 3 , 1 . Ее можно увидеть на рисунке:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

1. Если прямая, имеющая направляющий вектор a → = ( a x , a y ) , проходит через две точки – M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , то уравнение для нее может быть записано как в виде x — x 1 a x = y — y 1 a y , так и x — x 2 a x = y — y 2 a y .

2. Если заданная прямая имеет направляющий вектор с координатами a → = ( a x , a y ) , то множество всех ее векторов можно обозначить как μ · a → = ( μ · a x , μ · a y ) , μ ∈ R , μ ≠ 0 . Таким образом, любое уравнение прямой в каноническом виде x — x 1 μ · a x = y — y 1 μ · a y будет соответствовать этой прямой.

Разберем важный пример задачи на нахождение канонического уравнения.

В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M 1 ( 2 , — 4 ) и имеет направляющий вектор с координатами a → = ( 1 , — 3 ) . Запишите каноническое уравнение, описывающее данную прямую.

Решение

Для начала вспомним общий вид нужного нам канонического уравнения – x — x 1 a x = y — y 1 a y . Подставим в него имеющиеся значения x 1 = 2 , y 1 = — 4 , a x = 1 , a y = — 3 и подсчитаем:

x — x 1 a x = y — y 1 a y ⇔ x — 2 1 = y — ( — 4 ) — 3 ⇔ x — 2 1 = y + 4 — 3

Получившееся в итоге равенство и будет нужным ответом.

Ответ: x — 2 1 = y + 4 — 3

Канонические уравнения прямой на плоскости с a x или a y , равными нулю

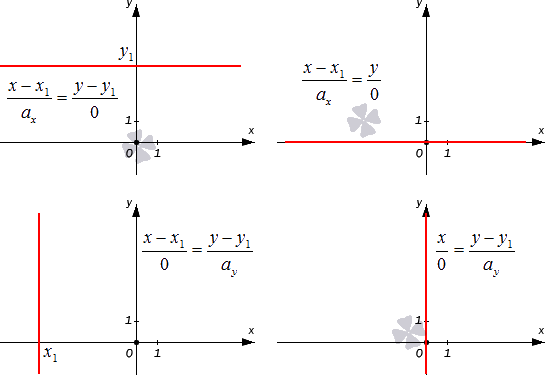
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x — x 1 a x = y — y 1 a y условной и понимать ее как равенство a y ( x — x 1 ) = a x ( y — y 1 ) .

Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x — x 1 0 = y — y 1 a y при a x = 0 , а исходная прямая будет проходить через M 1 ( x 1 , y 1 ) . В таком случае она является параллельной оси ординат (если x 1 = 0 , то она будет с ней совпадать). Докажем это утверждение.

Для этой прямой вектор a → = ( 0 , a y ) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j → = ( 0 , 1 ) .

Если же нулевым является значение второго параметра, то есть a y = 0 , то мы получаем равенство вида x — x 1 a x = y — y 1 0 . Это уравнение описывает прямую, проходящую через M 1 ( x 1 , y 1 ) , которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a → = ( a x , 0 ) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i → = ( 1 , 0 ) .

Проиллюстрируем два частных случая канонического уравнения, описанные выше:

На плоскости задана прямая, параллельная оси O y . Известно, что она проходит через точку M 1 2 3 , — 1 7 . Запишите каноническое уравнение для нее.

Решение

Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j → = ( 0 , 1 ) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:

x — 2 3 0 = y — — 1 7 1 ⇔ x — 2 3 0 = y + 1 7 1

Ответ: x — 2 3 0 = y + 1 7 1

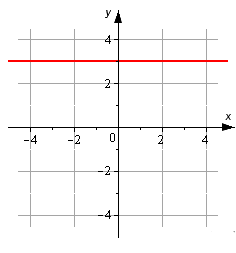
На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Мы видим, что исходная прямая проходит параллельно оси O x через точку M 1 ( 0 , 3 ) . Мы берем координатный вектор i → = ( 1 , 0 ) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.

x — 0 1 = y — 3 0 ⇔ x 1 = y — 3 0

Ответ: x 1 = y — 3 0

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Стандартной форме записи канонического уравнения x — x 1 a x = y — y 1 a y можно поставить в соответствие систему параметрических уравнений на плоскости x = x 1 + a x · λ y = y 1 + a y · λ . Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ . После этого надо выполнить разрешение получившихся равенств относительно переменных x и y :

x — x 1 a x = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y = λ ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Покажем на примере, как именно выполняется это действие с конкретными числами.

У нас есть прямая, заданная на плоскости с помощью канонического уравнения x + 2 3 = y — 1 11 . Запишите параметрические уравнения исходной прямой.

Решение

Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x + 2 3 = λ y — 1 11 = λ .

Далее можно перейти к формулированию необходимых параметрических уравнений:

x + 2 3 = λ y — 1 11 = λ ⇔ x + 2 = 3 · λ y — 1 = 11 · λ ⇔ x = — 2 + 3 · λ y = 1 + 11 · λ

Ответ: x = — 2 + 3 · λ y = 1 + 11 · λ

Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись a b = c d можно представить в виде a · d = b · c с сохранением смысла. Значит, что x — x 1 a x = y — y 1 a y ⇔ a y ( x — x 1 ) = a x ( y — y 1 ) ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 .

Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров a y = A , — a x = B , — a y x 1 + a x y 1 = C .

Прямая на плоскости описана с помощью канонического уравнения x — 1 2 = y + 4 0 . Вычислите общее уравнение этой прямой.

Решение

Делаем указанные выше действия по порядку.

x — 1 2 = y + 4 0 ⇔ 0 · ( x — 1 ) = 2 · ( y + 4 ) ⇔ y + 4 = 0

Ответ: y + 4 = 0 .

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

На плоскости задана прямая с помощью уравнения x + 3 3 = y — 2 2 . Запишите уравнение этой же прямой в отрезках.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

x + 3 3 = y — 2 2 ⇔ 2 · ( x + 3 ) = 3 · ( y — 2 ) ⇔ 2 x — 3 y + 6 + 2 3 = 0

Далее переходим к формулировке уравнения прямой в отрезках.

2 x — 3 y + 6 + 2 3 = 0 ⇔ 2 x — 3 y = — 6 + 2 3 ⇔ ⇔ 2 — ( 6 + 2 3 ) x — 3 — ( 6 + 2 3 ) y = 1 ⇔ x — 6 + 2 3 2 + y 6 + 2 3 3 = 1 ⇔ x — 3 + 3 + y 3 3 + 2 = 1

Ответ: x — 3 + 3 + y 3 3 + 2 = 1

Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – A x + B y + C = 0 . При условии A ≠ 0 мы можем перенести B y вправо с противоположным знаком. Получим A x + C = — B y . Теперь выносим A за скобки и преобразуем равенство так:

Получившееся уравнение мы записываем в виде пропорции: x + C A — B = y A .

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

А как сделать преобразование, если B ≠ 0 ? Переносим все слагаемые, кроме A x , вправо с противоположными знаками. Получаем, что A x = — B y — C . Выносим — B за скобки:

Формируем пропорцию: x — B = y + C B A

Есть общее уравнение прямой x + 3 y — 1 = 0 . Перепишите его в каноническом виде.

Решение

Оставим с левой стороны только одну переменную x . Получим:

Теперь вынесем — 3 за скобки: x = — 3 y — 1 3 . Преобразуем равенство в пропорцию и получим необходимый ответ:

Ответ: x — 3 = y — 1 3 1

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Прямая на плоскости описана с помощью системы параметрических уравнений x = 3 + 0 · λ y = — 2 — 4 · λ . Запишите каноническое уравнение для этой прямой.

Решение

Для начала преобразуем исходные уравнения в систему x = 3 + 0 · λ y = — 2 — 4 · λ . Следующим шагом будет выражение параметра в каждом уравнении:

x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

На плоскости задана прямая, каноническое уравнение которой имеет вид x — 1 2 = y + 1 2 — 3 . Выясните, лежат ли на ней точки M 1 3 , — 3 1 2 и M 2 ( 5 , — 4 ) .

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

3 — 1 2 = — 3 1 2 + 1 2 — 2 ⇔ 1 = 1

Результат говорит нам, что точка M 1 3 , — 3 1 2 принадлежит исходной прямой.

Точно так же поступим и с координатами второй точки:

5 — 1 2 = — 4 + 1 2 — 3 ⇔ 2 = 7 6

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Есть две точки M 1 ( 2 , 4 ) и M 2 ( — 1 , 3 ) . Будет ли прямая, которая задана в той же плоскости с помощью уравнения x — 2 0 = y — 3 2 , проходить через них?

Решение

Вспомним, что запись x — 2 0 = y — 3 2 можно понимать как 2 · ( x — 2 ) = 0 · ( y — 3 ) ⇔ x — 2 = 0 . Подставим координаты заданных точек в это равенство и проверим.

Начнем с первой точки M 1 ( 2 , 4 ) : 2 — 2 = 0 ⇔ 0 = 0

Равенство верное, значит, эта точка расположена на заданной прямой.

Подставляем данные второй точки: — 1 — 2 = 0 ⇔ — 3 = 0 .

Равенство неверное, значит, точка M 2 ( — 1 , 3 ) не лежит на исходной прямой.

Ответ: через точку M 1 ( 2 , 4 ) прямая проходит, а через M 2 ( — 1 , 3 ) нет.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Прямая на плоскости проходит через точку M 1 ( 0 , — 3 ) и через точку M 2 ( 2 , — 2 ) . Сформулируйте для этой прямой канонической уравнение.

Решение

Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M 1 M 2 → = 2 , 1 . По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:

x — 0 2 = y — ( — 3 ) 1 ⇔ x 2 = y + 3 1

Также можно использовать координаты второй точки. Тогда мы получим: x — 2 2 = y — ( — 2 ) 1 ⇔ x — 2 2 = y + 2 1

Ответ: x 2 = y + 3 1

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Известно, что точка M 1 ( 1 , 3 ) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x 2 = y — 5 . Запишите каноническое уравнение первой прямой.

Решение

Для первой прямой можно определить направляющий вектор a → = 2 , — 5 . Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x — 1 2 = y — 3 — 5

Ответ: x — 1 2 = y — 3 — 5

Через точку M 1 ( — 1 , 6 ) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2 x — 4 y — 7 = 0 . Запишите каноническое уравнение первой прямой.

Решение

Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2 , 4 . Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:

x — ( — 1 ) 2 = y — 6 4 ⇔ x + 1 1 = y — 6 2

Типовые задачи с плоскостями

Составление уравнений плоскостей

Разнообразие видов уравнений плоскостей порождается многообразием геометрических способов их задания. По любому набору геометрических данных, однозначно определяющих плоскость, можно составить уравнение этой плоскости, причем геометрические данные будут отражены в коэффициентах уравнения. И наоборот, коэффициенты любого уравнения плоскости имеют геометрический смысл, соответствующий способу задания плоскости.

Для удобства решения типовых задач, связанных с плоскостями, все основные типы уравнений плоскостей и соответствующие геометрические способы задания этих плоскостей отражены в таблице 4.1.

Примеры составления плоскостей по геометрическим данным указанны в таблице 4.1.

Таблица 4.1. Основные типы уравнений плоскостей

Метрические приложения уравнений плоскостей

Перечислим формулы для вычисления длин отрезков (расстояний) и величин углов по уравнениям образующих их плоскостей.

1. Расстояние от точки до плоскости вычисляется по формуле:

2. Расстояние между параллельными плоскостями и находится как расстояние от точки , координаты которой удовлетворяют уравнению до плоскости пo формуле:

3. а) Угол между двумя плоскостями и находится по формуле:

где и — нормали к плоскостям и соответственно.

находится величина того двугранного угла, образованного плоскостями и в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями.

При решении задач свойства 1-3 используются наряду с метрическими приложениями векторной алгебры.

Пример 4.12. В координатном пространстве заданы вершины треугольной пирамиды Требуется:

а) составить общее уравнение плоскости, содержащей грань ;

б) найти расстояние от вершины до плоскости грани ;

в) найти величину угла между плоскостями граней и ;

г) найти величину двугранного угла, образованного гранями и пирамиды.

Решение. а) По формуле (4.21) составим уравнение плоскости проходящей через три точки

Разлагая определитель по первой строке, получаем

Итак, искомое уравнение составлено.

б) Для нахождения расстояния составим уравнение плоскости, проходящей через точки (см. пункт «а»):

Расстояние находим по формуле пункта 1 (см. метрические приложения) для

в) Острый угол между плоскостями и находим по формуле пункта 3,»а»:

г) Двугранный угол , образованный гранями и пирамиды либо равен острому углу между плоскостями граней, либо дополняет его до Вычисляя угол по формуле пункта 3,»б», получаем тот же результат, что и в пункте «в»: т.е. острому углу принадлежат точки, принадлежащие разноименным полупространствам. Выясним, в каких полупространствах (одноименных или разноименных) относительно плоскостей граней и лежит пирамида. Для этого достаточно проверить одну точку пирамиды, не принадлежащую граням и Возьмем точку — середину ребра (рис.4.23). Вычислим значения линейных четырехчленов в этой точке:

Следовательно, точка принадлежит одноименным полупространствам. Поэтому двугранный угол при ребре не острый, а тупой, т.е.

Системы линейных уравнений с тремя неизвестными

Системой линейных алгебраических уравнений с тремя неизвестными называется система уравнений вида

Числа называются коэффициентами системы; — свободными членами; — неизвестными.

Решением системы называется такая упорядоченная тройка чисел что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство. На системы с тремя неизвестными переносятся все термины, применяемые к системам с двумя неизвестными.

Матричная запись неоднородной системы уравнений (4.29) имеет вид

где — матрица системы, — столбец свободных членов, – столбец неизвестных.

Рангом системы уравнений (4.29) называется ранг матрицы системы: т.е. максимальное число линейно независимых строк матрицы (максимальное число линейно независимых уравнений системы).

Рассматривается случай, когда все уравнения системы первой степени, т.е. коэффициенты при неизвестных каждого уравнения не равны нулю одновременно. Поэтому матрица системы ненулевая, более того, все ее строки ненулевые.

Поскольку матрица системы (4.29) ненулевая и содержит три столбца, то ее ранг Ранг может быть равен либо единице ( если все строки матрицы пропорциональны), либо двум ( если имеются две линейно независимые строки), либо трем ( , если имеются три линейно независимые строки).

Выясним геометрический смысл и свойства решений системы уравнений (4.29).

Пусть в пространстве задана аффинная система координат Множество точек координаты которых удовлетворяют линейному уравнению с тремя неизвестными

представляет собой плоскость. Поэтому множество решений системы уравнений является пересечением плоскостей

Рассмотрим примеры пересечения плоскостей .

1. Если ранг системы (4.29) равен 1, то коэффициенты при неизвестных всех уравнений пропорциональны. В этом случае любые две плоскости параллельны (система уравнений несовместна (рис.4.24,а)) или совпадают (в этом случае вся система (4.29) равносильна одному, например, первому ее уравнению (рис.4.24,б)).

2. Если ранг системы равен 2, то в системе имеются два линейно независимых уравнения. Плоскости, соответствующие этим уравнениям, пересекаются, например, по прямой (рис. 4.24,в,г). Поэтому множеством решений системы (4.29) является либо эта прямая (система совместна, все плоскости проходят через прямую т.е. все плоскости принадлежат собственному пучку плоскостей (рис. 4.24,в)), либо пустое множество (система несовместна (рис.4.24,г)).

3. Если ранг системы равен 3, то в системе имеются три линейно независимых уравнения. Плоскости, соответствующие этим уравнениям, пересекаются в одной точке, например, в точке (рис. 4.24,д,е). Поэтому множеством решений системы (4.29) является либо одна точка (система совместна, все плоскости проходят через точку т.е. все плоскости принадлежат собственной связке плоскостей (рис. 4.24,д)), либо пустое множество (система несовместна (рис. 4.24,е)).