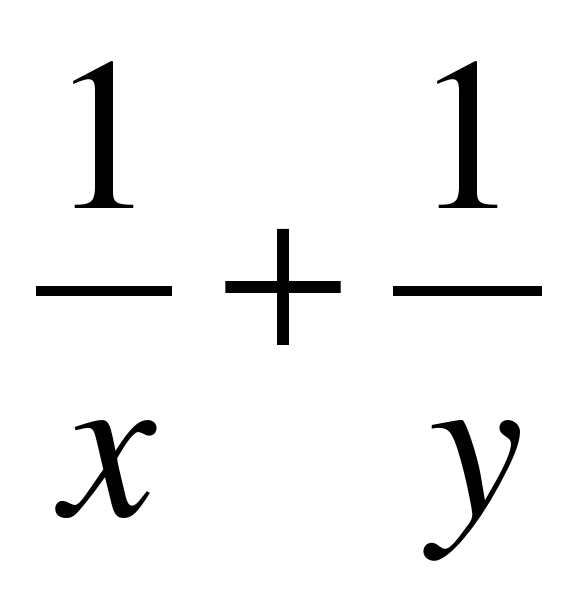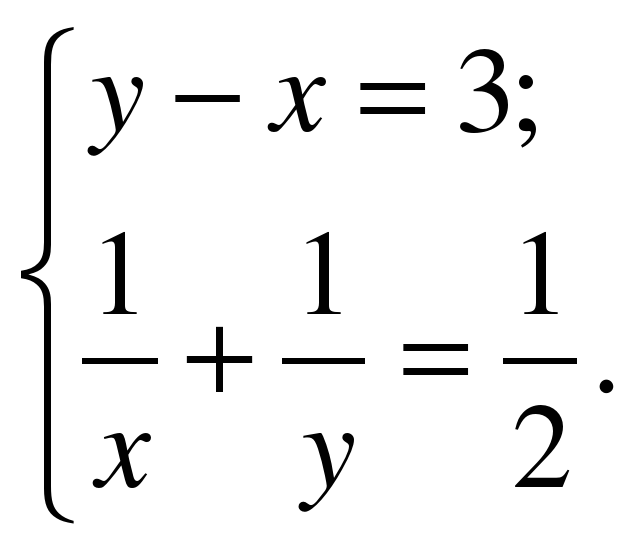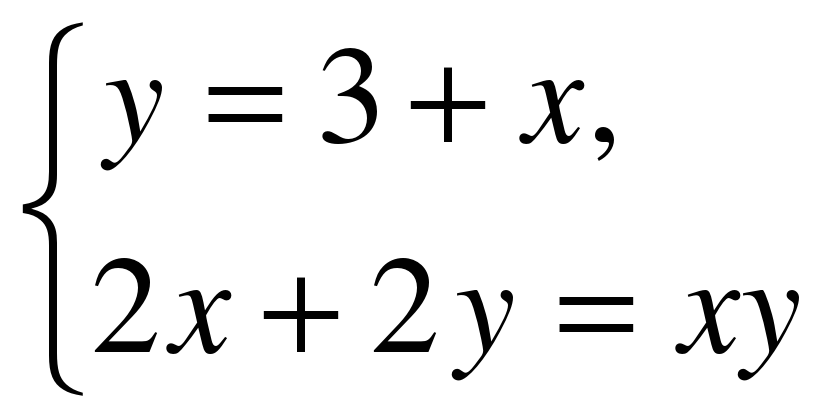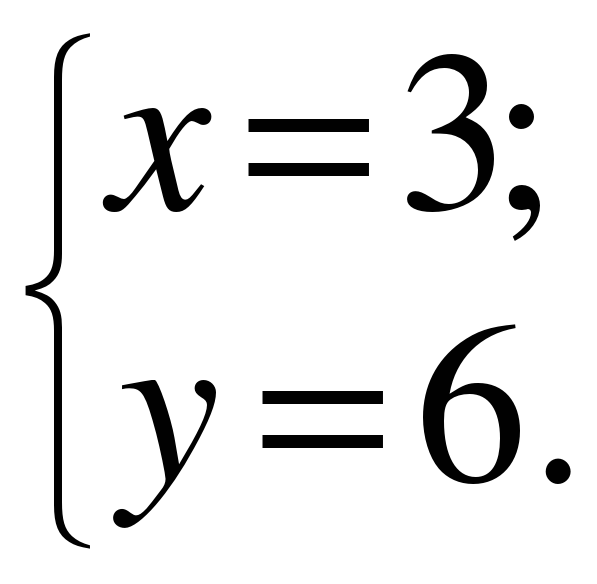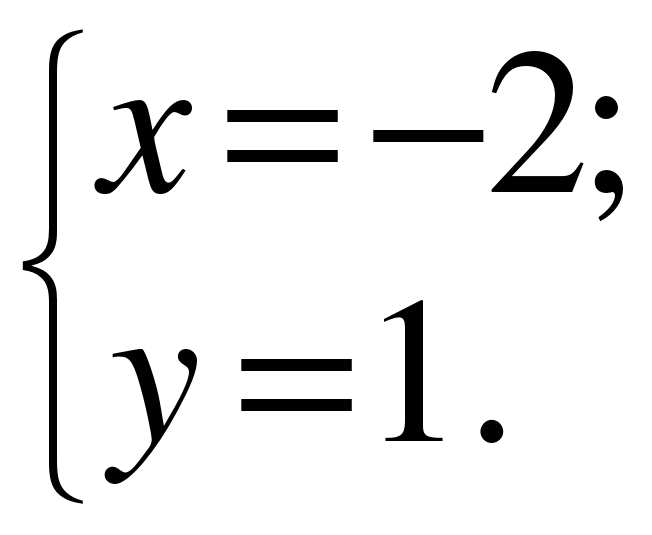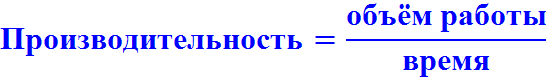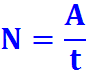Задачи на составление системы уравнений на работу

Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?

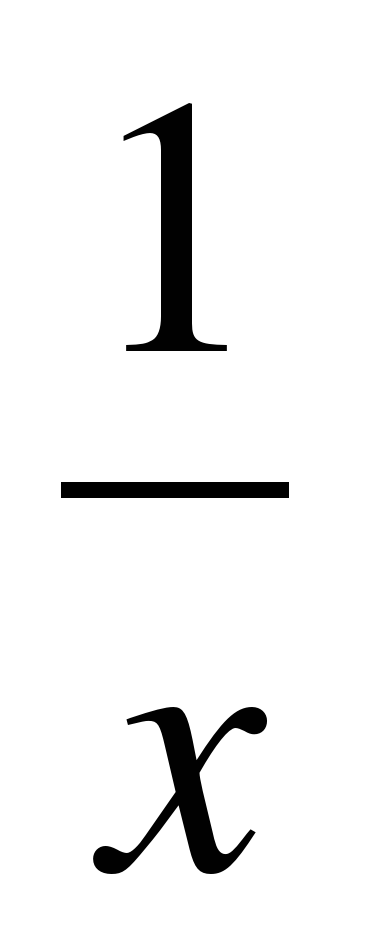
Пусть первый оператор может выполнить данную работу за x часов, а второй за y часов. За один час первый оператор выполняет часть всей работы, а второй . Составим систему уравнений:

Ответ: первый оператор за 12 ч, второй оператор за 24 ч.

На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?

Предположим, что ученик делает x деталей в час, . Тогда мастер делает детали в час.

Составим таблицу по данным задачи:

Производительность (дет/ч)	Время (ч)	Объём работ (дет)
Ученик	x		231
Мастер			462

Так как ученик потратил на работу на 11 часов больше, можно составить уравнение:

Решим уравнение, предварительно разделив обе части на 11:

Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.

Практикум по алгебре по теме «Задачи на работу»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практикум по алгебре по теме «Задачи на работу»

Данная методическая разработка посвящена проблеме под готовки обучающихся к сдаче ЕГЭ. В разработке представлен ряд задач по теме «Задачи на работу». Разработка представляет теоретическую и практическую пользу для обучающихся 10-11 классов и для учителей математики поскольку содержит примеры решения основных типов задач, а также набор задач для самостоятельного решения с ответами. Актуальность разработки состоит в том, что задачи на данную тему включены в КИМы профильного ЕГЭ по математике.

Текстовые задачи являются традиционным разделом школьного курса математики. Как правило, основная трудность при решении текстовой задачи состоит в переводе её условий на математический язык .

Любая задача состоит из трёх частей: условие, объект, вопрос задачи.

Приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования, каковы условия, исходя из которых надо её решать. Всё это называется анализом задачи .

Стандартная схема решения таких задач включает в себя:

1 .Выбор и обозначение неизвестных.

2. Составление уравнений (возможно неравенств) или системы уравнений с использованием неизвестных и всех условий задачи.

3 .Решение полученных уравнений (неравенств).

4. Отбор решений по смыслу задачи.

Задачи на работу содержат в себе информацию о выполнении некоторой работы несколькими субъектами (рабочими, механизмами и т. п.). К задачам на работу относят также задачи на заполнение резервуаров (так называемые задачи на трубы и бассейны). В качестве произведенной работы рассматривают объем перекачанной жидкости.

Задачи этого типа аналогичны задачам на движение. Вся работа играет роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения. Представим это в виде таблицы:

Время движения — t

Время работы — t

Производительность (скорость работы)

При этом мы понимаем, что работа есть, например, изготовление деталей, заполнение бассейна и т.п.

Производительность труда -это та же самая скорость работы, то есть часть работы, выполненная за единицу времени. Например, сколько деталей было изготовлено за час или на какую часть был заполнен бассейн за час и т.д.

Производительность может быть выражена в числах (10 деталей в час) или частью от всей работы (четверть поля в день, четверть бассейна в час).

Все эти задачи решаются по одной формуле: A = p t , то есть объем произведенной работы – это производительность (часть работы, выполненная за единицу времени), умноженная на время работы. Эта формула полностью аналогична формуле пройденного пути:

Из формулы A = p t можно выразить производительность (скорость работы): или время работы: .

1. Для начала внимательно читаем условие, стараемся выяснить всю информацию, содержащуюся в задаче.

2. Определяем, какую величину обозначить переменной x . Используя формулы A = p t , или , выражаем другие величины.

3. Единицы измерения, в которых записываются работа, время и производительность, должны быть согласованы.

4. Переводим условие задачи на математический язык, то есть составляем уравнение или систему уравнений.

5. Решаем полученную математическую модель. Из полученных решений выбираем те, которые подходят по смыслу задачи.

Разберем несколько задач.

Писатель собрался напечатать на компьютере 300 страниц текста. Если бы он печатал на 5 страниц в день больше, чем запланировал, то смог бы завершить работу на 3 дня раньше. Какое количество страниц в день запланировал печатать писатель?

Из условия понятно, что в задаче рассматриваются две ситуации: запланированная и произошедшая фактически.

В этой задаче объем работы известен, он явный и равен в том и в другом случае тремстам страницам.

Какую величину удобнее всего обозначить за x ? То, что требуется найти, то есть скорость работы по плану. Так и сделаем. Пусть скорость работы по плану равна x страниц в день, где x тогда фактическая скорость работы равна ( x страниц в день, потому что она по условию на 5 страниц в день больше.

Чтобы найти время работы, нужно воспользоваться формулой , то есть объем работы разделить на скорость работы. То есть время работы по плану равно дней, а фактическое время работы равно дней. Занесем эти данные в таблицу, в результате чего она примет вид:

Объем работы А (количество страниц)

Производительность работы P (количество страниц в день)

Теперь составить уравнение для решения задачи уже несложно. Используем то условие, что по факту работа была выполнена на 3 раньше запланированного срока. То есть запланированное время работы минус фактическое время работы равно 3 дням:

(можно составить такие уравнения: или ).

Решим первое уравнение.

Приведем дроби в левой части к одному знаменателю. Получим:

Умножим обе части уравнения на выражение x ( x при условии, что Получим: 3 x ( x .

Выполним преобразования и получим: 3 x 2 .

Разделим обе части уравнения на 3: x 2 .

Мы получили квадратное уравнение. Находим дискриминант по формуле D = b 2 – 4 ac .

D = 25 + 2000 = 2025. Находим корни по формуле = .

Ясно, что значение переменной 25 не подходит по смыслу задачи, производительность не может быть отрицательной.

Итак, писатель планировал печатать 20 страниц в день.

Ответ: 20 страниц в день.

Решение задач на трубы и бассейны не имеет никаких специфических черт по сравнению с другими задачами на совместную работу. Только рабочим будут соответствовать трубы или насосы разной производительности, а объему работы — объем бассейна (резервуара). Под производительностью трубы или насоса будем понимать объем воды, пропускаемой ими за единицу времени. Рассмотрим такую задачу.

Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько

литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?

Давайте обозначим переменной x производительность второй трубы, где x тогда первая труба за одну минуту пропускает ( x литров воды в минуту, причем x Объем работы каждой трубы мы знаем и можем выразить время работы каждой трубы:

минут – время работы 1 трубы, минут – время работы 2 трубы.

Объем работы А (литры)

Производительность P (литры в минуту)

По условию задачи известно, что время работы второй трубы на 10 минут меньше, чем первой .

Получим уравнение: = + 10; = 10;

Приводим левую часть уравнения к общему знаменателю: = 10;

После домножения обеих частей уравнения на уравнение примет вид:

D = 1225 + 3000 = 4225; = 7,5; = 25.

= 7,5 не соответствует смыслу задачи, производительность не может быть отрицательной. Значит, мы нашли, что вторая труба пропускает в минуту 25 литров воды.

Ответ : 25 литров воды в минуту.

Важно знать следующее:

1. Во многих задачах на работу точный объем работы неизвестен (тракторист вспахивает поле, бассейн заполняется трубами и т.п.). В этом случае удобно принять объем всей работы за единицу и измерять части такой работы в долях от единицы.

2. Если работа выполняется совместно несколькими объектами (так называемая совместная работа), то их общая производительность является суммой производительностей отдельных объектов.

Рассмотрим несколько задач на совместную работу.

В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?

Можно обойтись арифметическим способом, не прибегая к введению переменной.

Производительность (скорость работы) у первого насоса равна литров в минуту, а у второго насоса — литров в минуту. Скорость совместной работы насосов + ) л/мин = л/мин. Применим формулу для того, чтобы узнать время, за которое оба насоса вместе перекачают 25 литров воды.

Вот еще одна задача.

Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня – на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?

Так как количество вопросов теста неизвестно, обозначим их количество переменной x , где x .

Тогда время, необходимое Пете, равно часа, а время, необходимое Ване, равно часа. Петя потратил на выполнение теста на 20 минут, то есть на часа больше, чем Ваня. Поэтому получим такое уравнение: = . Приведем левую часть к общему знаменателю: = , откуда

Ответ: тест содержит 24 вопроса.

Один рабочий может выполнить задание на 5 ч. быстрее другого. Оба вместе они выполняют это задание за 6 ч. За сколько часов каждый из них выполнит задание?

Проведем анализ задачи. Во-первых, объем работы в задаче не определен, поэтому обозначим его за 1. Обозначим переменной x часов — время работы первого рабочего, причем x , тогда время работы второго рабочего будет равно ( x часов.

Выразим производительность каждого рабочего, используя формулу .

– производительность первого рабочего (часть задания, выполняемого им за 1 час),

– производительность второго рабочего,

+ – их совместная производительность (часть задания, выполняемого ими вместе за 1 час). Заполним таблицу:

При составлении уравнения можно рассуждать так: + – совместная производительность двух рабочих, то есть такую часть задания они выполняют за 1 час, работая вместе. На выполнение всего задания им потребуется 6 часов. Воспользуемся формулой A = p t и получим уравнение: ( + ) 6 = 1

Решим полученное уравнение.

После домножения обеих частей уравнения на уравнение примет вид:

Поскольку время – величина положительная, то x = 10.

За 10 часов выполнит задание первый инструктор, а второй – за 10+5=15 (часов).

Ответ: 10 ч, 15 ч.

Решая эту задачу на этапе составления уравнения можно поступить так:

так как все задание оба инструктора вместе выполняют за 6 часов, то — их совместная производительность (часть задания, которую они выполняют вместе за 1 час). С другой стороны, она выражена как + . Тогда получается следующее уравнение:

Далее приходим к квадратному уравнению x 2 x 30 = 0

Ответ: 10 ч, 15 ч.

При решении задач на совместную работу можно вводить не одну, а две переменные и получать систему уравнений.

Задача 6 . Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому.

Пусть объем всей работы равен 1.

Пусть х часов – время работы первого по выполнению всей работы, а у часов – время работы второго рабочего.

По условию второму рабочему для выполнения всей работы понадобится на 1 час больше, чем первому, то получим, что х=у– 1, и первое уравнение составлено.

Тогда – производительность труда первого рабочего, – производительность труда второго рабочего.

Так как они работали 45 мин или часа совместно, то

(– объем работы, выполненной рабочими за 45 минут.

Так как второй рабочий работал один 2 часа 15 минут = 2 часа = часа, то

– объем работы, выполненной вторым рабочим за 2 часа 15 минут.

Так как вся работа складывалась из часа совместной работы и часа работы второго рабочего, то получим второе уравнение:

Таким образом, мы получили систему двух уравнений:

Решим ее, для этого выражение для х из первого уравнения подставим во второе:

Из двух значений для у выберем то, которое подходит по смыслу задачи: , то есть 45 минут, но 45 минут рабочие работали вместе, а потом второй рабочий работал еще отдельно, поэтому не подходит по смыслу задачи. Для полученного у ₂ = 4 найдем из первого уравнения первоначальной системы значение х :

Ответ: первый рабочий выполнит работу за 3 часа, второй – за 4 часа.

Замечание : эту задачу можно было решить, не вводя вторую переменную у , а выразить время работы второго рабочего через х , тогда нужно было составить одно уравнение и решить его.

Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько может выполнить ту же работу первый рабочий самостоятельно, если он за два дня выполняет ту же часть работы, что и второй за три дня?

1. Поскольку в задаче работа никак численно не охарактеризована, то есть речь не идет об определенном количестве деталей или литров, то удобно весь объем работы принять за единицу: А = 1.

2. В качестве переменных удобно брать производительность труда. Обозначим производительность первого рабочего x , это будет часть работы, выполняемая первым рабочим за один день; y – соответственно, производительность второго рабочего.

3. Можем составить первое уравнение исходя из того, что вместе рабочие выполняют работу за 12 дней. Их общая производительность равна сумме двух производительностей, то есть x + y – это часть работы, выполняемая двумя рабочими за один день. По условию задачи, работая вместе, оба рабочих могут выполнить работу за 12 дней. Получим уравнение: 12 ( x + y ) = 1.

Заметим, что производительности труда рабочих складывать можно, а время работы нельзя, то есть, если один выполняет работу за 20 часов, а второй – за 30 часов, то вдвоем они выполнят ее не за 50 часов, а намного быстрее.

4. Составляем второе уравнение: 2 x = 3 y , оно соответствует фразе: за два дня первый выполняет ту же часть работы, что и второй за три дня. Первый выполняет за один день x , тогда очевидно, что за два дня выполнит в два раза больше, то есть 2 x ; аналогично, второй за три дня выполняет 3 y , и эти величины по условию задачи равны.

5. Получим систему двух уравнений с двумя неизвестными:

Вычтем из первого уравнения второе. Получим: и отсюда: 20;

Так, мы нашли производительность труда первого рабочего, она составляет , это та часть работы, которую первый рабочий выполняет за день.

Чтобы найти, за сколько дней первый рабочий выполнит самостоятельно всю работу, составляем уравнение:

где – время первого рабочего. Отсюда = 20.

Так, всю работу первый рабочий самостоятельно выполнит за 20 дней, что и требовалось найти.

Ответ: за 20 дней.

Два экскаватора разной мощности, работая совместно, выполняют работу за 6 часов. Если первый проработает 4 часа, а затем второй 6 часов, то они выполнят 80% всей работы. За какое время каждый экскаватор отдельно может выполнить всю работу?

Объем работы неизвестен, поэтому примем его за 1.

Пусть х – производительность первого экскаватора (часть работы, которую выполняет первый экскаватор за 1 час), а у – производительность второго экскаватора (часть работы, которую выполняет второй экскаватор за 1 час).

х + у – совместная производительность (часть работы, которую выполняют оба экскаватора вместе за 1 час).

Так как экскаваторы работают совместно 6ч с производительностью х + у и при этом выполняют всю работу, то составим уравнение: ( х + у ) 6 = 1.

Первый экскаватор работает 4ч с производительностью х , а затем 6ч второй экскаватор с производительностью у , и выполняют 0,8 всей работы, то 4 х + 6 у = 0,8. Решим систему уравнений:

Вычтем из первого уравнения второе. Получим уравнение с одной переменной: 2 х= 0,2. Отсюда х = 0,1.

Подставим в первое уравнение вместо переменной х значение 0,1:

Поскольку время, необходимое для выполнения всей работы, и производительность связаны соотношением и , то = 10, а 1 : = 15.Значит, первый экскаватор может выполнить всю работу за 10 часов, а второй – за 15 часов. Ответ: 10ч, 15ч.

Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики подкрасят забор, работая втроем?

Обозначим выполняемую мальчиками работу по покраске забора за 1.

Пусть Игорь красит забор за х часов, Паша за у часов, а Володя – за z часов. Тогда их производительности будут такими: у Игоря – , у Паши – , а у Володи — то есть такую часть забора может покрасить каждый из них за 1 час.

По условию задачи Игорь и Паша красят забор за 9 часов , значит, вместе они за 1 час покрасят забора. Получим уравнение: + = .

Составим и решим систему уравнений.

Сложим почленно все уравнения системы, получим:

Разделим полученное уравнение на 2:

Пусть искомое время, за которое мальчики покрасят забор, работая втроем, равно t . Воспользуемся формулой A = P t и получим уравнение:

Итак, мальчики покрасят забор, работая втроем, за 8 часов.

За один час Игорь и Паша красят забора, Паша и Володя красят забора, а Володя и Игорь красят забора. Работая вместе, за один час два Игоря, два Паши и два Володи покрасили бы

+ + = = забора. Значит, весь забор они покрасили бы за 4 часа. Но поскольку каждый из мальчиков был учтен два раза, то в реальности они могут покрасить забор за 8 часов.

Ответ: за 8 часов.

За сколько часов может выполнить работу каждый из трех рабочих, если производительность труда третьего рабочего равна полусумме производительностей труда первого и второго? Известно, что если бы третий рабочий проработал один 48 ч., то для окончания работы первому требовалось бы 10ч., а второму 15ч.

1) Обозначим объем работы за 1.

Пусть x – производительность первого рабочего, а y — производительность второго рабочего. В соответствии с условием задачи — производительность третьего рабочего.

48() + 10 x = 1 — работа, выполненная первым и третьим рабочими.

48() + 15 y = 1 — работа, выполненная вторым и третьим рабочими.

Составим и решим систему уравнений:

Вычитаем из первого уравнения второе, получаем = 0.

2) Таким образом, — производительность первого рабочего, — производительность второго рабочего.

( : 2 = = — производительность третьего рабочего.

3) Осталось найти время работы каждого рабочего.

1: = 50 (ч) – время первого рабочего,

1: = 75 (ч) – время второго рабочего,

1: = 60 (ч) – время первого рабочего.

Ответ: 50 ч; 75 ч; 60 ч.

Задачи для самостоятельного решения

1. В помощь садовому насосу, перекачивающему 8 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 36 литров воды?

2. Олег и Алексей выполняют одинаковый тест. Олег отвечает за час на 10 вопросов теста, а Алексей – на 12. Они одновременно начали отвечать на вопросы теста, и Олег закончил свой тест позже Алексея на 29 минут. Сколько вопросов содержит тест?

3. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 638 литров она заполняет на 7 минут быстрее, чем первая труба заполняет резервуар объемом 812 литров?

5. Коля и Петя красят забор за 16 часов, Петя и Андрей красят этот же забор за 20 часов, а Андрей и Коля — за 48 часов. За сколько часов мальчики покрасят забор, работая втроем?

6. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

7. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

8. Аквариум наполняется водой через две трубки за 3 часа. За сколько часов может наполниться аквариум через первую трубку, если для этого потребуется на 2,5 часа меньше, чем для наполнения аквариума через вторую трубку?

9. Плиточник должен уложить 175 м 2 плитки. Если он будет укладывать на 10 м 2 в день больше, чем должен, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день должен укладывать плиточник?

10. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

11. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

12. Двое рабочих, работая вместе, могут выполнить работу за 18 дней. За сколько дней, работая отдельно, выполнит эту же работу второй рабочий, если он за 6 дней делает столько же, сколько первый за 4 дня?

13. Для разгрузки баржи имеется три крана. Первому крану для разгрузки всей баржи требуется времени в четыре раза меньше, чем второму, и на 9 часов больше, чем третьему. Три крана, работая вместе, разгрузили бы баржу за 18 часов, но по условиям эксплуатации одновременно могут работать только два крана. Определите наименьшее время (в часах) необходимое для разгрузки баржи.(Производительность каждого крана постоянна в течении всей работы)

14. Заказ по выпуску машин завод должен выполнить за 20 дней, но уже за 18 дней завод перевыполнил план на 6 машин, так как ежедневно выпускал на 3 машины сверх плана. Сколько машин выпустил завод?

15. Два слесаря получили заказ. Сначала 1ч работал первый слесарь, затем 4ч они работали вместе. В результате было выполнено 40% заказа. За сколько часов мог выполнить заказ каждый слесарь, если первому для этого понадобилось бы на 5 ч больше, чем второму?

16. При одновременной работе двух насосов разной мощности бассейн наполняется водой за 8 часов. После ремонта насосов производительность первого из них увеличилась в 1,2 раза., а второго – в 1,6 раза, и при одновременной работе насосов бассейн стал наполняться за 6 часов. За какое время наполнится бассейн при работе только первого насоса после ремонта?

Ответы к задачам на работу для самостоятельного решения

1. Ответ: 7 минут

2. Ответ: 29 вопросов

3. Ответ: 10 деталей в час

4. Ответ: 29 литров

5. Ответ: за 15 часов

6. Ответ: 9 часов

7. Ответ: 6 минут

8. Ответ: 5 часов

10. Ответ: 9 часов

11. Ответ: 4 часа

12. Ответ: за 20 дней

13. Ответ: 20 часов

15. 25 часов и 20 часов

Гущин Д.. Решу ЕГЭ [электронный ресурс]. – URL: https://mathb-ege.sdamgia.ru/ [19.06.2020]

Ларин А.. ALEXLARIN . NET [электронный ресурс]. – URL: https://alexlarin.net/ [10.06.2020]

ФИПИ. Открытый банк заданий ЕГЭ [электронный ресурс]. – URL: https://fipi.ru/ege/otkrytyy-bank-zadaniy-ege [20.05.2020]

Краткое описание документа:

Разработка урока «Решение задач на работу»

Системы уравнений как математические модели реальных ситуаций. Задачи на совместную работу.Урок закрепления и применений знаний в новых условиях.

Просмотр содержимого документа
«Разработка урока «Решение задач на работу»»

УМК (название учебника, автор, год издания)

Алгебра 9 класс Авт.: А.Г. Мордкович, М.: Мнемозина -2010

Системы уравнений как математические модели реальных ситуаций. Задачи на совместную работу.

Общее количество часов, отведенное на изучение темы

Место урока в системе уроков по теме

4 урок по теме. Урок закрепления и применений знаний в новых условиях.

Научить учащихся решать задачи на работу с помощью систем уравнений как математических моделей реальных ситуаций.

Общеобразовательные: познакомить учащихся с применением систем уравнений при решении задач на работу; обеспечить овладение основными алгоритмическими приемами применения систем уравнений при решении задач на работу; формировать умения переносить знания в новую ситуацию, закрепить знания и умения учащихся в решении систем уравнений различными методами

Развивающие: развитие аналитического мышления; познавательной активности мышления, умения работать с текстовой, графической информацией через использование задач моделирующих жизненные ситуации

Воспитательные: формирование умения работать в группе.

Учащийся должен знать:

алгоритм решения задач на работу с помощью систем уравнений.

Учащийся должен уметь:

составлять систему уравнений к условию задач на работу;

использовать таблицы при интерпретации задач на работу;

исследовать построенную модель;

работать в группах, индивидуально.

Техническое обеспечение урока

интерактивная доска, мультимедиапроектор, презентация по теме урока

Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)

А.Г. Мордкович Алгебра . 9 класс.: В двух частях: Учеб. для общеобразовательных учреждений.-5-е изд. – М.: Мнемозина, 2013,

http://interneturok.ru/algebra/9-klass/algebra-9-klass-a-g-mordkovich; http://problems.ru/; https://math-oge.sdamgia.ru/

Урок №4. Тема: Системы уравнений как математические модели реальных ситуаций. Задачи на совместную работу.

1. Организационный момент.

Здравствуйте, друзья! Рада приветствовать Вас на нашем уроке.

Ещё Платон говорил: «Человек, способный к математике, изощрён во всех науках». (Слайд 2)

Как вы понимаете это высказывание?

Таким образом, мы сегодня будем размышлять, искать простые и красивые решения, развивать логическое мышление, правильно и последовательно рассуждать, тренировать память, внимание.

3. Актуализация опорных знаний. Проверка д/з.

Вспомним что мы изучали на предыдущем уроке

Решение задач на движение с помощью системы уравнений как математической модели реальных ситуаций

Давайте вспомним алгоритм составление математической модели

Составление математической модели.

Работа с составленной моделью.

Ответ на вопрос задачи.

Каков алгоритм решения задач на движение с помощью системы уравнений?

Обозначить неизвестные величины буквами.

Выразить оставшиеся неизвестные величины.

Найти в задаче условия для составления уравнений.

Решить получившуюся систему.

Найденное решение использовать для ответа на вопрос задачи

Назовите основные методы решения системы уравнений

Алгебраического сложения, подстановки, введение новых переменных.

Эти алгоритмы и способы решения систем уравнений Вы должны были применить при выполнении домашнего задания.

Давайте откроем рабочие тетради и начнём проверку домашнего задания с №7.2.

Я его тоже решала, и вот что у меня получилось. Всё ли у меня получилось верно? (Слайд 5) (Фронтальная проверка) №7.19 (Слайд 6).

4. Фиксация затруднений в индивидуальной деятельности.

Самостоятельная работа. Задания для самостоятельной работы. Приложение1.

Учащиеся проверяют результаты выполнения самостоятельной работы по эталону и проговаривают вместе с учителем вслух те понятия, алгоритмы из теоретической базы, на которые они допустили ошибки. (Слайды 7-9). При проверке задания 1 остановиться на анализе неверного ответа на слайде 4, обосновать свой ответ.

Сегодня на уроке мы начнем рассматривать решение еще одного вида задач с помощью систем уравнений второй степени с двумя переменными.

5. Изучение нового материала.

Дорогие ребята! Область применения математике очень широка. Рассмотрим старинную задачу из математической рукописи XYII века. (Слайд 10).

Два плотника рядились двор ставить. И говорит первый:

— Только бы мне одному двор ставить, то я бы поставил на 3 года быстрее.

А другой молвил:

— А если бы мы работали ладно, управились и за 2 года.

Сколько долго они ставили двор по одиночке? Кому отдал предпочтение хозяин?

Откройте тетради, запишите число, сформулируйте тему урока (Слайд 11).

Давайте проанализируем ситуации задачи и оформим анализ условия в виде таблицы, аналогичной таблицам задач на движение.

О каких ситуациях (процессах) идет речь в задаче?- о работе

Сколько ситуаций (процессов) описано в задаче?- работа 1 плотника, работа 2 плотника, совместная работа

Какими величинами характеризуется каждый процесс, описанный в задаче?- производительность, время, работа

Как будем решать задачу? – составим систему

С чего начнем? – обозначим неизвестные величины буквами

Как обозначим эти неизвестные величины? — обозначим за х лет время выполнения работ первого плотника, а у лет время выполнения работ второго

Занесите все известные данные в таблицу самостоятельно. Что у вас получилось? (заполняют таблицу на доске самостоятельно)

Что делаем дальше? – выразим оставшиеся величины.

Можем ли мы сейчас это сделать? – нет, не хватает данных

Что можно сказать об объеме выполняемой работы? (Объем работы один и тот же, но не выражен числом) Если объем выполненной работы неизвестен, т.е. нет никаких данных, позволяющих его найти — работа принимается за единицу

Что делаем дальше? – выразим оставшиеся величины (Слайд 13)

Если работая вместе, всю работу плотники выполняют за 2 года, то какую часть работы выполнят они вместе, работая 1 год? – 1/2

Что дальше? – найдем условия для составления уравнений

Выделим эти условия.

– Первый плотник, работая один, мог бы выполнить работу на 3 года быстрее, чем второй. (Слайд 13)

— Работая вместе, могут выполнить работу за 2 года.

Составим пояснительный текст задачи.

Пусть х лет время работы первого плотника, а у лет время работы второго плотника. Известно, что время выполнения всей работы первым плотником меньше на 3 года, чем время работы второго плотника. Составим первое уравнение системы у-х=3.

Используя третью строку таблицы, получим второе уравнение системы .

Составим и решим систему уравнений:

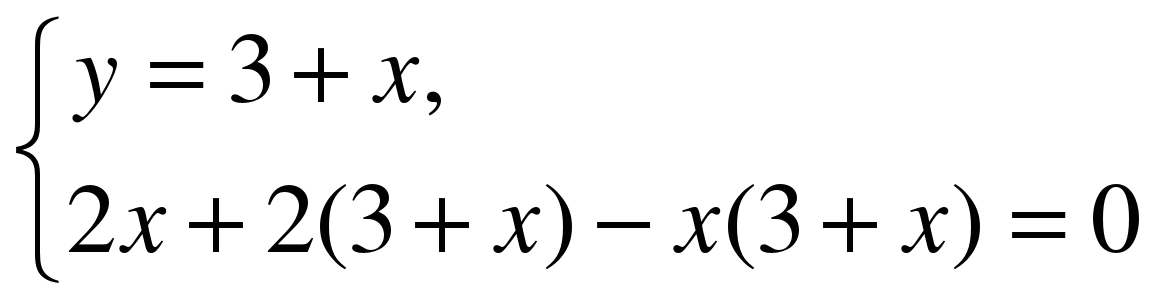
не удовлетворяет условию задачи

Ответ: 3 года и 6 лет.

Что необходимо знать? (Слайд 14)

1. Объём, выполняемой работы! (A)

2. Время работы! (t)

3. Производительность! (N)

Что необходимо делать? (Слайд 15)

Про себя повтори

Нет объёма работы, за 1 прими

Данные в таблицу занеси

Включение с систему знаний и повторения. Приложение 2

А теперь поработаем в группах. На столах у каждой группы в конвертах лежит задание. Каждое задание состоит из двух частей. Вам предстоит решить задачу и в бланк ответа вписать составленную систему, которая позволит решить задачу, а далее необходимо решить данную систему и выбрать правильный вариант ответа предложенный ниже. После чего один представитель от каждой группы должен внести эти результаты в компьютер, тем самым проверить правильность выполнения задания. Каждый учащийся в группе получит отметку, зависящую от того, насколько удачно сработает его группа.

(Контроль учителя за работой групп)

Задача 1. Мастер, работая самостоятельно, может изготовить партию из 200 деталей за некоторое время. Ученик за это же время может изготовить только половину всех деталей. Работая вместе, они могут изготовить всю партию деталей за 4 ч. За какое время мастер может изготовить все детали, работая самостоятельно? Заполняется карточка (рис 1).

источники:

http://infourok.ru/praktikum-po-algebre-po-teme-zadachi-na-rabotu-4418704.html

http://multiurok.ru/index.php/files/razrabotka-uroka-rieshieniie-zadach-na-rabotu.html

Задачи на составление системы уравнений на работу