Система уравнений Максвелла
Первое уравнение Максвелла в интегральной формеявляется обобщением закона электромагнитной индукции Фарадея в форме

Согласно Максвеллу этот закон справедлив не только для проводящего контура, но и для любого замкнутого контура, мысленно выбранного в переменном магнитном поле. Иными словами, с переменным магнитным полем независимо от того, находятся в нём проводники или нет, неразрывно связано вихревое электрическое поле.
Переменное электрическое поле, так же как и электрический ток, является источником магнитного поля. Количественной мерой магнитного действия переменного электрического поля служит ток смещения. Плотностью тока смещенияназывается вектор:
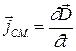


где 
Третье уравнение Максвелла в интегральной форме

где r — объемная плотность свободных электрических зарядов.
Четвёртое уравнение Максвелла в интегральной форме

Систему уравнений Максвелла необходимо дополнить так называемыми материальными уравнениями, характеризующими электрические и магнитные свойства среды.
В случае изотропных несегнетоэлектрических и неферромагнитных сред и макротоков, подчиняющихся закону Ома, эти уравнения имеют вид



где e0, m0 — электрическая и магнитная постоянные; e, m — относительные диэлектрическая и магнитная проницаемости среды; s — удельная электрическая проводимость среды.
Примеры решения задач
1. Квадратная рамка со стороной а=2 см, содержащая 100 витков, подвешена на упругой нити с постоянной кручения С=10 мкН×м/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определить индукцию магнитного поля, если при пропускании по рамке тока I=1А она повернулась на угол j=60 о .
Решение



где р m = NIS = NIa 2 — магнитный момент рамки; В — индукция магнитного поля; a — угол между вектором 
Из условия равновесия
Ia 2 NB sin a — Сj = 0,
B = Сj/(Ia 2 NB sin a).
Подставим числовые значения:
В = 10 -3 ×60 / 1×4×100×0,5 = 30 мТл.
2. Прямой бесконечный проводник имеет круговую петлю радиусом R=80 см. Определить силу тока в проводнике, если известно, что в точке А магнитная индукция B = 12,5 мкТл.



Векторы В1 и В2 на рисунке в точке А будут направлены в одну сторону перпендикулярно плоскости рисунка от нас, тогда можно записать
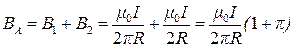

Подставим числовые значения:

3. Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током I0 =5 А. Сторона рамки 8 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти поток вектора 


Прямой проводник с током создает вокруг себя неоднородное магнитное поле с индукцией

которая уменьшается с увеличением расстояния от проводника. Направление вектора индукции будет совпадать с направлением нормали к рамке. Так как магнитное поле неоднородное, поверхность, ограниченную рамкой, разобьём на элементарные площадки dS = a×dr, в пределах которых магнитную индукцию можно считать постоянной величиной (см. рисунок). Тогда поток магнитной индукции (магнитный поток) через элементарную площадку
Полный поток вектора 

Подставим числовые значения:
Фm = 4p×10 –7 ×5×0,08×(ln 2)/2p = 5,545×10 –8 Вб.

Решение
Так как силовые линии магнитного поля замкнуты, то магнитный поток и индукция магнитного поля в сердечнике и в воздушном зазоре одинаковы: В1=В2. Для решения задачи воспользуемся теоремой о циркуляции вектора 


где Н1 и Н2 — напряжённости магнитного поля в сердечнике и вне его; l1 и l2 – длина железного сердечника и межполюсного пространства.
Поскольку величина В1 известна по условию задачи, то величину Н1 найдём из графика зависимости В = В(H) (прил. 1):
при В = 1,3 Тл, Н = 800 А/м.
Из уравнения (1) определим число ампер-витков электромагнита:
(NI) = 800×0,4 + 1,3×0,01/(4×3,14×10 –7 ) = 1,07×10 4 А-вит.
Величину ЭДС e вычислим по закону Ома:
e=IRпров = Irl пров/S = IrpDN / S = IrpDN / S.
Подставим числовые значения:
e = 1,7×10 –8 ×3,14×0,05×1,07×10 4 /10 –6 = 29 В.
Для определения толщины обмотки нужно знать общее число витков N и число витков N1 в одном слое обмотки.
где l1 – длина сердечника; d – диаметр провода обмотки: d = 
N1 = l1/ 

Зная число ампер–витков и предельно допустимое значение силы тока (I=jS), определим общее число витков N
N = (NI)/(jS) = 1,07×10 4 / (3×10 6 ×10 –6 ) = 3567 витков.
Тогда толщина обмотки
b = d×k = k× 

5. Квадратная рамка с током I=1 А расположена в одной плоскости с длинным прямым проводником с током I0=5 А. Сторона рамки 10 см. Ось рамки, проходящая через середины противоположных сторон, параллельна проводу и отстоит от него на расстоянии, которое в n = 1,5 раза больше стороны рамки. Найти:
1) силу, действующую на рамку;
2) работу, которую нужно совершить для поворота рамки вокруг её оси на 180°, если токи поддерживают неизменными.
Решение

Как видно из рисунка (при указанных направлениях силы тока в проводниках), l=a, a=90° (sin a =1), силы 

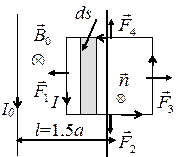

Следовательно, результирующая этих двух сил равна нулю. Силы 

Так как сила F1 в два раза больше силы F3, то результирующая этих сил будет совпадать по направлению с силой F1, а по величине
Подставим числовые значения
F = 4p×10 –7 ×1×5/4p = 5×10 –7 Н = 0,5 мкН.
2. Работу, необходимую для поворота рамки с током I на 180°, можно определить по формуле
где Ф1m и Ф2m — магнитные потоки через поверхность рамки в начальном и конечном состояниях. Так как магнитное поле проводника с током I0 неоднородное, сначала определим магнитный поток через элементарную площадку dS=adr, в пределах которой индукцию магнитного поля можно считать постоянной величиной:
а полный магнитный поток сквозь рамку в начальном и конечном состояниях


Подставим числовые значения:
А = –4p×0,1×1×5×0,69×10 –7 /p » –1,4×10 –7 Дж = –0,14 мкДж .
6. Тонкий металлический стержень длиной l = 1,2 м вращается в однородном магнитном поле вокруг перпендикулярной к стержню оси, отстоящей от одного из его концов на расстоянии а=0,25 м, делая n=120 об/мин. Вектор магнитной индукции поля параллелен оси вращения и имеет величину В=10 –3 Тл. Найти разность потенциалов U, возникающую между концами стержня.
Решение



Для однородного магнитного поля и плоской поверхности dФm=BdScosa, или, подставив в (1), получаем (знак минус опустим, так как необходимо найти только величину ЭДС)

По условию задачи cosa =1, поэтому из выражения (2) следует

dj = wdt = (2pn)dt. (4)
Подставляя (4) в (3), получим:

U = 10 –3 ×2p×2 (1,2 2 + 2×1,2×0,25)/2 = 0,0128 В = 12,8 мВ.
7. Прямой проводник длиной l=10 см помещён в однородное магнитное поле с индукцией В=1 Тл. Концы проводника замкнуты гибким проводом, находящимся вне поля. Сопротивление внешней цепи R=0,4 Ом. Какая мощность потребуется для того, чтобы двигать проводник перпендикулярно линиям индукции с постоянной скоростью u=20 м/с?

Проведём анализ условия задачи. При движении проводник будет пересекать линии индукции. За счёт этого в проводнике возникнет ЭДС индукции
где в данном случае
dФ = BdS = Bludt . (2)
Подставляя (2) в (1), получаем:
Сила индукционного тока в цепи согласно закону Ома
Тепловая мощность, выделяемая на внешнем сопротивлении
P = I 2 R = B 2 l 2 u 2 /R.
Эта мощность будет равна мощности, которую необходимо подводить к системе за счёт внешней силы, действующей на проводник, для того, чтобы скорость движения проводника была постоянной. Таким образом:
P = B 2 l 2 u 2 /R = 1×0,01×400/0,4 = 10 Вт.
8. Две катушки равномерно намотаны на цилиндрический сердечник, длина которого много больше диаметра. Индуктивность первой катушки 0,2 Гн, второй- 0,8 Гн. Сопротивление второй катушки 600 Ом. Какой ток потечёт по второй катушке, если ток в 0,3 А, текущий в первой катушке, выключить в течение времени 0,001 с.

Данная задача относится к разделу взаимной индукции. Сила тока во вторичной обмотке
Величина e2 зависит от взаимной индуктивности L12 и быстроты изменения силы тока I1
Взаимная индуктивность двух соленоидов, имеющих общий сердечник, рассчитывается по формуле
поэтому, учитывая выражения (3), (4), (5), получаем
L12 = 
Подставляя выражение (6) в выражение (2), а полученный результат — в выражение (1), получаем:
I2 = (L12I 01)/R2 = (I01 
I2 = 
9. На тороид квадратного поперечного сечения намотано 1000 витков провода. Внутренний радиус тороида равен 0,1 см, внешний — 0,2 см. Магнитная проницаемость тороида равна100. По обмотке тороида протекает электрический ток силой 1 À. Определить энергию магнитного поля внутри тороида.

Решим задачу двумя способами.
1. Энергия магнитного поля – это энергия, запасённая в индуктивности:
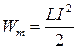
где L — индуктивность, I — сила тока, протекающего в индуктивности.
Потокосцепление, согласно определению индуктивности, рассчитывается как
где Фm — магнитный поток через поперечное сечение S тороида.

где r — расстояние от центра тороида до площадки dS, на которой определяется величина индукции магнитного поля. Так как тороид квадратного сечения, то высота площадки h = (r 2 — r 1), а ширина — dr. Поэтому

Тогда индуктивность тороида
L = 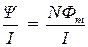


Подставляя выражение для индуктивности в выражение для энергии, получаем

Wm = 100×4p×10 –7 ×10 6 ×10 –3 ×1×ln2 /(4p) = 6,9 мДж.
2. Энергия магнитного поля Wm связана с плотностью энергии wm соотношением:
Wm = 
Выберем в качестве элемента объема dV объем цилиндрического слоя радиусом r, высотой h=(r2 — r1) и толщиной dr (в пределах этого слоя величина Н постоянна). Запишем выражение для dV=(r2 – r1)2pr·dr и подставим в выражение для энергии Wm. Получаем
W m = 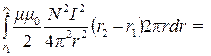


Подставим числовые значения и получим:
Как видим, оба решения дают одно и то же значение.
Примечание: если в условии задачи величина m не задана, а указано, что тороид представляет собой железный, стальной или чугунный сердечник, то величина m находится по графику зависимости В = В(Н) (прил. 1) как
В качестве величины Н принять значение Н в центральной точке поперечного сечения тороида.
Задачи для самоконтроля

2. 
I=2 A, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить ширину зазора l2.
3. a-частица, кинетическая энергия которой Ек=500 эВ, влетает в однородное магнитное поле, перпендикулярно к направлению её движения. Индукция магнитного поля В=0,1 Тл. Определить силу F, действующую на a-частицу, радиус R окружности, по которой движется a-частица, и период обращения Т a-частицы.
4. Квадратная рамка со стороной а=10 см, по которой течет ток I=200 А, свободно установилась в однородном магнитном поле (В=0,2 Тл). Определить работу, которую необходимо совершить при повороте рамки вокруг оси, лежащей в плоскости рамки и перпендикулярной линиям магнитной индукции, на угол j=2p/3 радиан.
Ответ: А=I·В·а 2 ·(1-cosj)=0,6 Дж.
5. Бесконечно тонкий проводник равномерно вращается с частотой n=10 об/с в однородном магнитном поле с индукцией В=0,01 Тл. Ось вращения, проходящая через один из концов проводника, параллельна линиям индукции и составляет угол a=30 о с осью проводника. Найти разность потенциалов между концами проводника, если его длина l = 0,1 м.
Ответ: 
6. Из провода радиусом а=1,00 мм сделана прямоугольная рамка, длина которой l=10,0 м значительно больше ширины b=0,10 м (измеренной между осями сторон рамки). Найти индуктивность рамки L. Магнитная проницаемость среды равна 1. Полем внутри проводов пренебречь.
Ответ: 
7. Две катушки расположены на небольшом расстоянии друг от друга. Когда сила тока в первой катушке изменяется с быстротой DI/Dt=5 А/с, во второй катушке возникает ЭДС индукции ei=0,1 В. Определить взаимную индуктивность катушек.
Ответ: Lвз = 
8. Напряженность магнитного поля тороида со стальным сердечником возросла от Н1=200 А/м до Н2=800 А/м. Определить, во сколько раз изменилась объемная плотность энергии магнитного поля.
Ответ: 
Контрольное задание № 4
401. По двум длинным параллельным проводам текут в противоположных направлениях токи силой I1=I2=I=10 А. Расстояние между проводами d=0,3 м. Определить магнитную индукцию в точке А, удаленной от первого и второго проводов соответственно на расстояния r1=0,15 м и r2=0,2 м.
402. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии а=4 см от его середины. Длина отрезка провода l=20 см, сила тока в проводе I=10 А.
403. Определить индукцию магнитного поля в центре проволочной квадратной рамки со стороной а=15 см, если по рамке течёт ток I=5 А.
404. Определить индукцию магнитного поля в центре контура, имеющего вид прямоугольника, если его диагональ d=16 см, угол между диагоналями j=30°, ток в контуре I=5 А.
405. Ток I=20 А течёт по длинному проводнику, согнутому под прямым углом. Определить индукцию магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на 10 см.
406. На рисунке изображены сечения двух прямолинейных бесконечно длинных проводников с токами. Расстояние между проводниками АВ=10 см, токи I1=20 А и I2=30 А. Определить индукцию В магнитного поля, вызванного токами I1 и I2 в точках М1, М2, М3. Расстояния М1А =2 см, АМ2 =4 см, ВМ3 =3 см. 408. Бесконечно длинный тонкий проводник с током I=50 А имеет изгиб радиусом R=10 см. Определить индукцию магнитного поля в точке О (в центре изгиба). 410. Тороид с железным сердечником, длина которого по средней линии l=1 м, имеет воздушный зазор l2=3 мм. По обмотке тороида, содержащей N=1300 витков, пустили ток, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить силу тока. 411. По проводнику, изогнутому в виде окружности, течёт ток. Индукция магнитного поля в центре окружности равна 25,1 мкТл. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определить индукцию магнитного поля в точке пересечения диагоналей этого квадрата. 412. Внутри соленоида длиной l=25,1 см и диаметром D=2 см помещён железный сердечник. Соленоид имеет N=200 витков. Определить магнитный поток Фm, если ток в соленоиде I=5 А. 413. Магнитная индукция В на оси тороида без сердечника (внешний диаметр тороида d1=60 см, внутренний — d2=40 см), содержащего N=200 витков, составляет 0,16 мТл. Пользуясь теоремой о циркуляции вектора 414. По прямому бесконечно длинному проводнику течёт ток I=10 А. Определить, пользуясь теоремой о циркуляции вектора 415. Тороид намотан на железное кольцо сечением S=5 см 2 . При силе тока I=1 А магнитный поток Фm=250 мкВб. Определить число витков n тороида, приходящихся на отрезок длиной 1 см средней линии кольца. 416. Электромагнит изготовлен в виде тороида. Сердечник тороида со средним диаметром d=51 см имеет вакуумный зазор длиной l0 =2 мм. Обмотка тороида равномерно распределена по всей его длине. Во сколько раз уменьшится индукция магнитного поля в зазоре, если, не изменяя силы тока в обмотке, зазор увеличится в n=3 раза? Рассеянием магнитного поля вблизи зазора пренебречь. Магнитную проницаемость m сердечника считать постоянной и принять равной 800. 417. Обмотка катушки сделана из проволоки диаметром d=0,8 мм. Витки плотно прилегают друг к другу. Считая катушку достаточно длинной, определить напряжённость H и индукцию B магнитного поля внутри катушки при токе I=1A. 418. Железное кольцо диаметром D=11,4 см имеет обмотку из N=200 витков, по которой течет ток I1=15A. Какой ток I2 должен проходить через обмотку, чтобы индукция в сердечнике осталась прежней, если в кольце сделать зазор шириной b=1 мм? Определить магнитную проницаемость m материала сердечника при этих условиях. 419. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой S=1 мм 2 . Длина соленоида l=25 см, диаметр D=5 см. Определить напряженность H и индукцию B магнитного поля внутри соленоида при токе I=2 A, если сопротивление соленоида R=0,2 Ом. Удельное сопротивление меди r=17·10 -9 Ом·м. 420. Внутри соленоида с числом витков N=200 с никелевым сердечником (m=200) напряженность однородного магнитного поля H=10 кA/м. Площадь поперечного сечения сердечника S=10 см 2 . Определить: 1) магнитную индукцию поля внутри соленоида; 2) потокосцепление. 421. По двум тонким проводам, изогнутым в виде колец радиусом R=10 см, текут одинаковые токи I=10 А в каждом. Найти силу взаимодействия этих колец, если плоскости, в которых лежат кольца, параллельны, а расстояние d между центрами колец равно 1мм. 422. Виток, диаметр которого d=20 см, может вращаться около вертикальной оси, совпадающей с одним из диаметров витка. Виток установили в плоскости магнитного меридиана и пустили по нему ток I=10 A. Какой вращающий момент нужно приложить к витку, чтобы удержать его в начальном положении? Горизонтальную составляющую Bг магнитной индукции поля Земли принять равной 20 мкТл. 423. Из проволоки длинной l=20 см сделаны квадратный и круговой контуры. Определить вращающие моменты сил M1 и M2, действующие на каждый контур, помещенный в однородное магнитное поле с индукцией В=0,1 Тл. По контурам течет ток I=2 A. Плоскость каждого контура составляет угол a=45° с направлением поля. 424. Электрон, ускоренный разностью потенциалов U=0,5 кВ, движется параллельно прямолинейному длинному проводнику на расстоянии r=1 см от него. Определить силу, действующую на электрон, если через проводник пропускать ток I=10 А. 425. Электрон движется в однородном магнитном поле с индукцией В=0,2 мТл по винтовой линии. Определить скорость v электрона, если радиус винтовой линии R=3 см, а шаг h=9 см. 426. Ионы двух изотопов с массами m1=6,5×10 –26 кг и m2=6,8×10 –26 кг, ускоренные разностью потенциалов U=0,5 кВ, влетают в однородное магнитное поле с индукцией В=0,5 Тл перпендикулярно линиям индукции. Принимая заряд каждого иона равным элементарному электрическому заряду, определить, насколько будут отличаться радиусы траекторий ионов изотопов в магнитном поле. 427. Частица, несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией В=0,5 Тл. Определить момент импульса L, которым обладала частица при движении в магнитном поле, если её траектория представляла собой окружность радиусом R=0,2 см. 428. Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью u=10 7 м/с. Длина конденсатора l=5 см. Напряжённость электрического поля конденсатора Е=10 кВ/м. При вылете из конденсатора электрон попадает в магнитное поле, перпендикулярное к электрическому полю. Индукция магнитного поля В=10 мТл. Найти радиус R и шаг h винтовой траектории электрона в магнитном поле. 429. Заряженная частица прошла ускоряющую разность потенциалов U=104 В и влетела в скрещенные под прямым углом электрическое (Е=10 кВ/м) и магнитное (В=0,1 Тл) поля. Определить отношение заряда частицы к её массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. 430. Протоны ускоряются в циклотроне в однородном магнитном поле с индукцией В=1,2 Тл. Ускоряющее напряжение 30 кВ. Максимальный радиус кривизны траектории протонов R=40 см. Определить: 1) какое количество оборотов сделает протон до приобретения максимальной кинетической энергии; 2) время ускорения протонов до ЕКмакс. 431. Два бесконечных прямолинейных параллельных проводника с одинаковыми токами, текущими в одном направлении, находятся друг от друга на расстоянии d. Чтобы их раздвинуть до расстояния 2d, на каждый сантиметр длины проводника затрачивается работа А=138 нДж. Определить силу тока в проводниках. 432. Квадратный проводящий контур со стороной l=20 см и током I=10 А свободно подвешен в однородном магнитном поле с индукцией В=0,2 Тл. Определить работу, которую необходимо совершить, чтобы повернуть контур на 180° вокруг оси, перпендикулярной направлению магнитного поля. 433. В однородном магнитном поле с индукцией В=0,2 Тл находится квадратный проводящий контур со стороной l=20 см и током I=10 А. Плоскость контура составляет с направлением поля угол a=30°. Определить работу удаления контура за пределы поля. 434. Круговой проводящий контур радиусом r=5 см и током I=1 А находится в магнитном поле, причём плоскость контура перпендикулярна направлению поля. Напряжённость магнитного поля Н=10 кА/м. Определить работу, которую необходимо совершить, чтобы повернуть контур на 90° вокруг оси, совпадающей с диаметром контура. 435. В однородном магнитном поле с индукцией В=0,5 Тл движется равномерно проводник длиной l=10 см. По проводнику течёт ток I=2 А. Скорость движения проводника u=20 см/с и направлена перпендикулярно к направлению магнитного поля. Определить работу А перемещения проводника за время t=10 с и мощность Р, затраченную на это перемещение. 436. В однородном магнитном поле с индукцией В=1 Тл находится плоская катушка из 100 витков радиусом r=10 см, плоскость которой с направлением поля составляет угол b=60°. По катушке течёт ток I=10 А. Определить работу, которую необходимо совершить, чтобы удалить эту катушку из магнитного поля. 437. По проводу, согнутому в виде квадрата со стороной длиной a=20 см, течет ток I=20 А, сила которого поддерживается неизменной. Плоскость квадрата составляет угол b=20° с линиями индукции однородного магнитного поля (B=0,1Тл). Вычислить работу, которую необходимо совершить для того, чтобы удалить провод за пределы поля. 438. Два прямолинейных длинных параллельных проводника находятся на расстоянии d1=10 см друг от друга. По проводникам в одном направлении текут токи I1=20 А и I2=30 А. Какую работу Al надо совершить (на единицу длины проводников), чтобы раздвинуть эти проводники до расстояния d2 =20 см? 439. По кольцу, сделанного из тонкого гибкого провода радиусом r=10 см, течет ток I=100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией В=0,1 Тл, по направлению совпадающей с индукцией В1 собственного магнитного поля кольца. Определить работу внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упругих сил пренебречь. 440. В однородном магнитном поле с индукцией В=0,01 Тл находится прямой провод длиной l=8 см, расположенный перпендикулярно линиям индукции. По проводу течёт ток I=2 А. Под действием сил поля провод переместился на некоторое расстояние S, при этом была совершена работа А=80 мкДж. Определить это расстояние S. 441. В магнитном поле, индукция которого изменяется по закону B=a+bt 2 , где b=10 -2 Тл/с 2 , расположена квадратная рамка со стороной a=20 см, причем плоскость рамки перпендикулярна вектору магнитной индукции. Определить ЭДС индукции в рамке в момент времени t=5 c. 442. Медный диск радиусом a=10 см вращается в однородном магнитном поле, делая 100 оборотов в секунду. Магнитное поле направлено перпендикулярно к плоскости диска и имеет напряженность H=7,96·10 5 А/м. Две щетки, одна на оси диска, другая на окружности, соединяют диск с внешней цепью, в которой включены последовательно резистор с сопротивлением R=10 Ом и амперметр. Что показывает амперметр? 443. Горизонтальный стержень длиной 1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельна силовым линиям магнитного поля, индукция которого равна 5·10 –5 Тл. При каком числе оборотов в секунду разность потенциалов на концах этого стержня будет 1 мВ? 444. В однородном магнитном поле, индукция которого равна 0,1 Тл, вращается катушка, состоящая из 200 витков. Ось вращения катушки перпендикулярна ее оси и направлению магнитного поля. Период вращения катушки равен 0,2 с, площадь поперечного сечения катушки 4 см 2 . Найти максимальную ЭДС индукции во вращающейся катушке. 445. В однородном магнитном поле, индукция которого 0,8 Тл, равномерно вращается рамка с угловой скоростью 15 рад/с. Площадь рамки 150 см 2 . Ось вращения находится в плоскости рамки и составляет 30 ° с направлением силовых линий магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке. 446. Скорость самолёта с реактивным двигателем равна 950 км/ч. Найти ЭДС индукции, возникающую на концах крыльев самолёта, если вертикальная составляющая напряжённости магнитного поля земли 39,8 А/м и размах крыльев самолёта 12,5 м. 447. В однородном магнитном поле с индукцией 1 Тл равномерно вращается рамка, содержащая 1000 витков провода. Площадь рамки 150 см 2 . Рамка вращается с частотой 10 об/с. Определить мгновенное значение ЭДС, соответствующее углу поворота рамки 30°. Ось вращения перпендикулярна линиям индукции и лежит в плоскости рамки. 448. Проволочный виток радиусом 4 см и сопротивлением 0,01 Ом находится в однородном магнитном поле с напряжённостью 5000 А/м. Плоскость рамки составляет 30° с линиями напряжённости. Какое количество электричества протечёт по витку, если магнитное поле выключить? 449. Проволочное кольцо радиусом R=10 см лежит на столе. Какое количество электричества q протечёт по кольцу, если его перевернуть с одной стороны на другую? Сопротивление кольца r=1 Ом. Вертикальная составляющая индукции магнитного поля земли В=50 мкТл. 450. Для измерения индукции магнитного поля между полюсами магнита помещена катушка, состоящая из 50 витков проволоки и соединённая с баллистическим гальванометром. Ось катушки параллельна направлению магнитного поля. Площадь поперечного сечения катушки 2 см 2 , сопротивлением её по сравнению с сопротивлением гальванометра можно пренебречь. Сопротивление гальванометра 2×10 3 Ом, его баллистическая постоянная 2×10 -8 Кл/дел. При быстром выдёргивании катушки из магнитного поля гальванометр даёт отброс, равный 50 делениям шкалы. Чему равна индукция магнитного поля? 451. В магнитном поле, индукция которого равна 0,05 Тл, помещена катушка, содержащая 200 витков проволоки. Сопротивление катушки 40 Ом, площадь её поперечного сечения 12 см 2 . Катушка помещена так, что её ось составляет 60 o с направлением магнитного поля. Какое количество электричества протечёт по катушке при исчезновении поля? 452. В однородном магнитном поле, индукция которого 1 Тл, находится прямой проводник длиной 20 см. Концы проводника замкнуты проводом, находящимся вне поля. Сопротивление всей цепи 0,1 Ом. Найти силу, которую надо приложить к проводнику, чтобы перемещать его со скоростью 2,5 м/с перпендикулярно линиям индукции. 453. Электрическая лампочка, сопротивление которой в горячем состоянии равно 10 Ом, подключается через дроссель к двенадцативольтовому аккумулятору. Индуктивность дросселя 2 Гн, сопротивление 1 Ом. Через сколько времени после включения лампочка загорится, если она начинает светиться при напряжении на ней 6 В? 454. Имеется катушка длиной 20 см и диаметром 2 см. Обмотка катушки состоит из 200 витков медной проволоки, площадь поперечного сечения которой 1 мм 2 . Катушка включена в цепь с некоторой ЭДС. При помощи переключателя ЭДС выключается и катушка замыкается накоротко. Через сколько времени после выключения ЭДС сила тока в цепи уменьшается в 2 раза? 455. Рамка площадью S=100 см 2 содержит N=1000 витков провода с сопротивлением r1=12 Ом. К концам обмотки подключено внешнее сопротивление r2=20 Ом. Рамка равномерно вращается в магнитном поле (B=0,1 Тл), делая n=2 об/с. Чему равно максимальное значение мощности переменного тока во внешней цепи? Ось вращения, лежащая в плоскости рамки, перпендикулярна линиям индукции. 456. Квадратная рамка из медной проволоки сечением 1 мм 2 помещена в магнитное поле, индукция которого меняется по закону B=B0sinwt, где B0=0,01 Тл, w=2p/T и T=0,02 c. Площадь рамки 25 см 2 . Плоскость рамки перпендикулярна к направлению магнитного поля. Найти максимальную силу тока, возникающую в рамке. 457. В соленоид длиной 50 см вставлен ферромагнитный сердечник. Число витков на единицу длины соленоида равно 400 вит./м. Найти индуктивность соленоида, если при силе тока 2 А по обмотке соленоида магнитный поток, пронизывающий поперечное сечение соленоида, равен 1,6 мВб. 458. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода. Диаметр провода 0,2 мм, диаметр соленоида 5 см. По соленоиду течёт ток силой 1 А. Определить, какое количество электричества протечёт через обмотку, если концы её замкнуть накоротко. 459. Тонкий медный проводник массой m=1 г согнут в виде квадрата и концы его замкнуты. Квадрат помещён в однородное магнитное поле (B=0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определить количество электричества q, которое протечёт по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию. 460. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой 1 мм 2 . Длина соленоида 25 см и сопротивление его обмотки 0,2 Ом. Найти индуктивность соленоида. Удельное сопротивление меди 1,7×10 –8 Ом×м. 461. На соленоид, длина которого равна 21 см и площадь поперечного сечения 10 см 2 , надета катушка, состоящая из 50 витков. Катушка соединена с баллистическим гальванометром, сопротивление которого 10 3 Ом. По обмотке соленоида, состоящей из 200 витков, идёт ток силой 5 А. Какой заряд пройдёт по гальванометру, если ток соленоида станет равным нулю? 462. На соленоид длиной 144 см и диаметром 5 см надет проволочный виток. Обмотка соленоида имеет 2000 витков и по ней течёт ток в 2 А. Соленоид содержит железный сердечник. Какая средняя ЭДС индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение 0,002 с? 463. Обмотка тороида имеет N1=251 виток. Средний диаметр тороида 8 см, диаметр витков 2 см. На тороид намотана вторичная обмотка N2, имеющая 100 витков. При замыкании первичной обмотки в ней в течение 0,001 с устанавливается ток силой 3 А. Найти среднее значение ЭДС индукции во вторичной обмотке. 464. На соленоид длиной 20 см и площадью поперечного сечения 30 см 2 надет проволочный виток. Соленоид имеет 320 витков и по нему течёт ток в 3 А. Какая средняя ЭДС индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение 0,001 с? 465. Две катушки имеют взаимную индуктивность, равную 0,005 Гн. В первой катушке сила тока изменяется по закону I=I0 sin wt, где I0=10 А, w=2p/T, T=0,02 с. Найти наибольшее значение ЭДС индукции во второй катушке. 466. Вычислить взаимную индуктивность длинного прямого провода и прямоугольной рамки со сторонами a и b. Рамка и провод лежат в одной плоскости, причём ближайшая сторона рамки длиной a параллельна проводу и отстоит от него на расстоянии l. 467. Два концентрических тонких проводника в форме окружностей с радиусами a и b лежат в одной плоскости (a –8 Кл? 470. Определить взаимную индуктивность L12 тороида и проходящего по его оси бесконечного прямого провода. Тороид имеет прямоугольное сечение ширины a. Внутренний радиус тороида r1, внешний r2. Число витков тороида N. Тороид и провод погружены в среду с проницаемостью m. 471. Длинный цилиндр радиусом R, заряженный равномерно по поверхности, вращается вокруг своей оси с угловой скоростью w. Найти энергию магнитного поля на единицу длины цилиндра, если линейная плотность заряда цилиндра равна l, а m=1. 472. При некоторой силе тока плотность энергии магнитного поля соленоида (без сердечника) w=0,2 Дж/м 3 . Во сколько раз увеличится плотность энергии этого поля при той же силе тока, если соленоид будет иметь железный сердечник? 473. Соленоид содержит N=1000 витков. Сила тока в обмотке I=1 А, магнитный поток через поперечное сечение соленоида Фm=0,01 Вб. Вычислить энергию магнитного поля. 474. Обмотка тороида содержит 10 витков на каждый сантиметр длины. Сердечник немагнитный. При какой силе тока плотность энергии магнитного поля равна 1 Дж/м 3 . 475. На стержень из немагнитного материала длиной l=50 см и сечением S=2 см 2 намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока в обмотке I=0,5 А. 476. На железное кольцо намотано в один слой N=200 витков. Чему равна энергия магнитного поля, если при токе I=2,5 А магнитный поток в железе 0,5 мВб? 477. По обмотке тороида течёт ток I=0,6 А. Витки провода диаметром d=0,4 мм плотно прилегают друг к другу. Найти энергию магнитного поля в стальном сердечнике тороида, если площадь поперечного сечения его S=4 см 2 , диаметр средней линии D=30 см. 478. Индукция магнитного поля тороида со стальным сердечником возросла от B1=0,5 Тл до B2=1 Тл. Найти, во сколько раз изменилась объёмная плотность энергии магнитного поля. 479. Катушка индуктивностью L=2 мкГн и сопротивлением R0=1 Ом подключена к источнику постоянного тока с ЭДС e=3 В. Параллельно катушке включено сопротивление R=2 Ом. После того как ток в катушке достигнет установившегося значения, источник тока отключается. Найти количество тепла, выделившееся на сопротивлении R после отключения источника. Сопротивлением источника и соединительных проводов пренебречь. 480. Железный сердечник, имеющий форму тора с квадратным сечением, несёт на себе обмотку из N=1000 витков. Внутренний радиус тора a=0,2 м, внешний b=0,25 м. Определить энергию, запасённую в сердечнике в том случае, если по обмотке течёт ток I=1,26 А. Определение произвести приближённо, полагая напряжённость поля по всему сечению тороида одинаковой и равной значению H в центре сечения. Варианты контрольного задания № 4
Библиографический список 1. Савельев, И. В. Курс общей физики: в 3 т. Т.2. Электричество и магнетизм. Волны. Оптика: учеб. пособие для втузов /И.В. Савельев. 3-е изд., испр. М., 1987. 496 с. 2. Трофимова, Т. И. Курс физики: учеб. пособие для инж.–техн. специальностей вузов /Т.И. Трофимова. 4 -е изд., испр. М.: Высш. школа, 1997. 542 с. 3. Курс физики: учебник для вузов: в 2 т. /Под ред. В. Н. Лозовского. 2-е изд., испр. СПб.: Лань, 2001. Т. 1. 576 с. 3. Детлаф, А. А., Яворский Б. М. Курс физики: учеб. пособие для втузов / А. А. Детлаф, Б. М. Яворский. 1989. 608 с. 4. Яворский, Б. М., Справочник по физике / Б.М. Яворский, А.А. Детлаф. 2-е изд., перераб. М.: Наука, 1985. 512 с. 5. Чертов, А. Г. Задачник по физике /А.Г. Чертов, А.А. Воробьёв. 5-е изд., перераб. и доп. М., 1988. 526 с. 6. Волькенштейн, В. С. Сборник задач по общему курсу физики: [для втузов] /В.С. Волькенштейн. 11-е изд. перераб. М.: Наука, 1985. 381 с. 7. Беликов, Б. С. Решение задач по физике. Общие методы: учеб. пособие для вузов / Б.С. Беликов. М.: Высш. школа, 1986. 255 с. Удельное сопротивление проводников (при 0 0 С), мкОмּм
Содержание Содержание теоретического курса . . . . . . 3 1. Электростатика и постоянный ток . . . . . 5 1.1. Электрический заряд. Закон сохранения заряда. Закон Кулона. Напряженность поля . . . . . 5 1.2. Принцип суперпозиции полей . . . . . . 7 1.3. Поток напряженности. Теорема Гаусса для электростатического поля в вакууме . . . . 8 1.4. Потенциал электростатического поля. Работа совершаемая силами электростатического поля при перемещении в нем электрического заряда . . . 9 1.5. Примеры применения теоремы Гаусса к расчету электростатических полей . . . . . . 10 1.6. Электрическое поле в диэлектрической среде. Дипольные моменты молекул диэлектрика. Поляризация диэлектрика . . . . . . 12 1.7. Теорема Гаусса для электростатического поля в среде . . 13 1.8. Условия для электростатического поля на границе раздела изотропных диэлектрических сред . . . . . 14 1.9. Проводники в электростатическом поле. Электроемкость проводника . . . . . . 14 1.10. Взаимная емкость. Конденсаторы . . . . . 15 1.11. Потенциальная энергия системы точечных зарядов. Энергия заряженного проводника и электрического поля . 16 1.12. Постоянный электрический ток. Сила и плотность тока . 16 1.13. Законы постоянного тока. Сторонние силы . . . 18 1.14. Правила Кирхгофа . . . . . . . 19 Примеры решения задач . . . . . . 20 Задачи для самоконтроля . . . . . . 28 Контрольное задание №3 . . . . . . 30 2. Магнетизм . . . . . . . . . 38 2.1. Сила Лорентца и сила Ампера. Вектор магнитной индукции . 38 2.2. Закон Био и Савара. Принцип суперпозиции. Магнитные поля прямого и кругового токов . . . 40 2.3. Магнитное взаимодействие проводников с токами. Контур с током в магнитном поле . . . . . 41 2.4. Циркуляция магнитного поля (закон полного тока) в вакууме. Теорема Гаусса для магнитного поля . . . . . 42 2.5. Работа перемещения проводника с током в магнитном поле . 43 2.6. Движение заряженных частиц в магнитном и электрическом полях . . . . . . . 44 2.7. Магнитные моменты электронов и атомов. Задачи на уравнения максвелла с решением и объяснениемТеория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента. Теория Максвелла — макроскопическая. Это означает, что рассматриваются макроскопические поля зарядов и токов, пространственные размеры которых неизмеримо больше размеров отдельных молекул и атомов. Математическим выражением теории Максвелла служит система из четырех уравнений, которые записывают в двух формах — дифференциальной и интегральной. Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса. Рассмотрим теорему Остроградского-Гаусса . Пусть для характеристики какого-либо поля выбран вектор . Тогда поток вектора через произвольную замкнутую поверхность S, мысленно проведенную в этом поле, равен интегралу от дивергенции вектора , взятому по объему V, ограниченному замкнутой поверхностью S:
Операция дивергенции над произвольным вектором сводится к пространственной производной вида:
где ax, ay, az — проекции вектора на оси прямоугольной декартовой системы координат. Рассмотрим теорему Стокса . Пусть для характеристики какого-либо поля выбран вектор . Тогда циркуляция вектора вдоль произвольного замкнутого контура L, мысленно проведенного в этом поле, равна потоку вектора rot через поверхность S, ограниченную замкнутым контуром L:
Векторная операция rot в декартовых координатах выражается так:
Первое уравнение МаксвеллаЭто уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:
Однако для произвольного контура выполняется взаимосвязь:
Поскольку в общем случае , то для не изменяющегося во времени контура имеет место соотношение:
Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:
Используя теорему Стокса, преобразуем (4.1.5):
Сравнивая подинтегральные выражения в (4.1.7) и в правой части (4.1.9), получим окончательно первое уравнение Максвелла в дифференциальной форме:
Физический смысл этого уравнения: переменное магнитное поле индуцирует вихревое электрическое поле. Второе уравнение МаксвеллаИспользуем теорему Гаусса для диэлектриков:
где — вектор электрической индукции, — вектор поляризации диэлектрика. Продифференцируем (4.1.11) по времени:
Если поверхность S — неподвижна и не деформируется, то изменение во времени потока вектора электрической индукции может быть связано только с изменением по времени самого вектора электрической индукции:
Правая часть этой формулы имеет размерность тока, следовательно, величина имеет размерность плотности тока. Максвелл предложил назвать эту величину плотностью тока смещения :
Введя представление о токе смещения, Максвелл по-новому подошел к рассмотрению условия замкнутости цепей электрического тока. Как известно, цепи постоянного тока должны быть замкнутыми. Однако для цепей переменного тока это условие уже не является обязательным. Например, при зарядке и разрядке конденсатора постоянный электрический ток протекает по проводнику, соединяющему обкладки, но не проходит через диэлектрик, находящийся между обкладками. Следовательно, цепь не замкнута. Однако, с точки зрения Максвелла, для переменного тока такая цепь замыкается благодаря току смещения, который протекает через такой участок, где нет проводника, т.е. через диэлектрик. На таком участке благодаря наличию переменного тока смещения обязательно возникает переменное магнитное поле. Однако действие тока смещения, приводящее к возникновению магнитного поля, нельзя отделить от действия обычного тока проводимости. Например, для прямолинейного тока проводимости можно записать:
Линии магнитного поля направлены по касательным к концентрическим окружностям, окружающим проводник с током. Найдем циркуляцию магнитного поля по замкнутому контуру в виде окружности радиуса r:
Следовательно, магнитное поле прямолинейного проводника — вихревое (циркуляция вектора магнитного поля по замкнутому контуру не равна нулю). Максвелл предположил, что в правой части соотношения (4.1.16) следует добавить ток смещения:
где ток смещения легко вычислить, используя (4.1.14):
Силу тока проводимости можно также представить в виде:
Согласно теореме Стокса для магнитного поля, имеем:
Подставляя (4.1.18) и (4.1.19) в (4.1.17) и сравнивая подинтегральные выражения в правой и левой частях, получаем второе уравнение Максвелла:
При отсутствии тока проводимости, тем не менее, может существовать переменное магнитное поле, обусловленное только током смещения:
Третье уравнение МаксвеллаМаксвелл обобщил теорему Гаусса для диэлектриков (4.1.11), предположив, что она справедлива для любого электрического поля, как стационарного, так и переменного. Запишем уравнение (4.1.11) в виде:
где ρсвоб — объемная плотность свободных зарядов, расположенных в объеме V, ограниченном замкнутой поверхностью S. Тогда, используя теорему Остроградского-Гаусса для вектора электрической индукции, получим:
Сравнивая подинтегральные выражения в (4.1.23) и (4.1.24), получим третье уравнение Максвелла:
Четвертое уравнение МаксвеллаПоскольку поток вектора магнитной индукции равен нулю:
то, используя теорему Остроградского-Гаусса для вектора магнитной индукции, легко получить четвертое уравнение Максвелла:
Такое равенство определяется отсутствием магнитных зарядов. Итак, полная система уравнений Максвелла в дифференциальной форме включает в себя четыре дифференциальных уравнения:
Эту систему необходимо дополнить материальными уравнениями , которые характеризуют электрические, и магнитные свойства конкретных сред (веществ). В случае изотропных несегнетоэлектрических и неферромагнитных сред и макроскопических токов, подчиняющихся закону Ома, эти уравнения в системе СИ имеют вид:
где ε0 и μ0 — электрическая и магнитная постоянные, ε и μ — относительная диэлектрическая и магнитная проницаемости среды, σ — удельная электропроводность вещества. 4.1.2. Свойства электромагнитных волнЭлектромагнитной волной называется распространяющееся в пространстве с определенной скоростью электромагнитное поле. Как следует из уравнений Максвелла, переменное электрическое поле непременно порождает переменное магнитное поле, которое затем индуктирует переменное электрическое поле. Поэтому следует говорить о неразрывной связи переменных электрического и магнитного полей, называя это явление электромагнитным полем . Очевидно, что такой процесс должен происходить, циклически повторяясь, в течение неограниченного времени, если нет поглощения. Существование электромагнитных волн непосредственно следует их уравнений Максвелла. Для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, эти уравнения приобретают вид:
Используя материальные уравнения (4.1.29), эти уравнения можно представить в виде:
Если записать эти уравнения в проекциях на оси декартовой системы координат, то получим:
Используя первое из уравнений (4.1.33), можно получить:
Следовательно, компонента Ех удовлетворяет волновому уравнению:
Если ввести обозначение для дифференциальной операции:
то волновое уравнение (4.1.37) можно представить в компактном виде:
Аналогичные уравнения могут быть получены и для всех других компонент электрического и магнитного полей. Суммируя результаты, окончательно можно представить волновые уравнения для электрического и магнитного полей в векторном виде:
Таким образом, переменное электромагнитное поле распространяется в среде в виде волн, фазовая скорость которых равна:
где
есть скорость электромагнитной волны в вакууме. Оказалось, что с = 3·10 8 м/с, что совпадает со скоростью света в вакууме. Поэтому Максвелл задолго до экспериментального обнаружения электромагнитных волн (Г. Герц, 1888 г.) высказал гипотезу о том, что свет — это тоже электромагнитная волна. Прямой проверкой можно показать, что решениями уравнений (4.1.39) служат плоские синусоидальные волны, которые удобно представить в форме Эйлера:
где ω — циклическая частота; — волновой вектор, перпендикулярный фронту плоской волны и задающий направление распространения волны; — радиус-вектор, задающий точки пространства. Операция ротора может быть сведена к векторному произведению, например:
Тогда, используя решения (4.1.42), с помощью (4.1.43) имеем:
следовательно, применение этой операции сводится к векторному произведению. Рассмотрим сейчас операцию:
Наконец, операцию дивергенции можно представить так:
Применяя результаты (4.1.44), (4.1.45) и (4.1.46) к уравнениям Максвелла (4.1.31), имеем: или, окончательно:
Из двух последних уравнений (4.1.47) следует, что , что указывает на поперечность электромагнитной волны. Из первого уравнения (4.1.47) ясно, что вектор Н как результат векторного произведения, должен быть перпендикулярен плоскости, в которой лежат вектора и . Аналогично, из второго уравнения (4.1.47) следует, что вектор электрического поля должен быть перпендикулярен плоскости, в которой лежат вектора и . Окончательно получается, что для любой электромагнитной волны вектора , и составляют тройку ортогональных векторов (Рис. 4.1.1). 4.1.3. Шкала электромагнитных волнВ зависимости от частоты ν = ω/2π или длины волны в вакууме λ0 = с/ν, а также способа излучения и регистрации различают несколько видов электромагнитных волн:
Радиволнами называются электромагнитные волны, у которых длина волны в вакууме λ0 > 5·10 -5 м (ν 12 Гц). Весь диапазон радиоволн принято делить на 9 поддиапазонов (Табл. 4.1.1).
Оптическим излучением или светом называются электромагнитные волны, у которых длина волны в вакууме лежит в диапазоне 10 нм >λ0 > 1 мм (границы условны). К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения. Инфракрасным (ИК) называются электромагнитные волны, испускаемые нагретыми телами, у которых длина волны в вакууме лежит в диапазоне 1 мм > λ0 > 770 нм. Видимым излучением (светом) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 770 нм > λ0 > 380 нм. Свет способен вызывать зрительные ощущения в человеческом глазе. Ультрафиолетовым излучением (УФ) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 380 нм > λ0 > 10 нм. Рентгеновским излучением (рентгеновскими лучами) называются электромагнитные волны, которые возникают при взаимодействии заряженных частиц и фотонов с атомами вещества. Оно характеризуется длинами волны в вакууме в диапазоне с условными границами (10-100 нм) > λ0 > (0,01-1 пм). Гамма-излучением (γ-лучами) называются электромагнитные волны с длинами волны в вакууме 0,1 нм > λ0. Это излучение испускается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также возникает при распаде частиц, аннигиляции пар «частица-античастица» и других процессах. 4.1.4. Световая волнаСвет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других — как поток особых частиц (фотонов). В электромагнитной волне колеблются векторы электрического и магнитного полей. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются наличием колебаний электрического вектора, который называют в этом случае световым вектором . Его изменения в пространстве и времени задаются уравнением плоской волны:
Здесь r — расстояние, отсчитываемое вдоль направления распространения волны. Отношение скорости световой волны в вакууме с к ее фазовой скорости v в некоторой прозрачной среде называется абсолютным показателем преломления этой среды:
Показатель преломления связан с относительными диэлектрической и магнитной проницаемостями соотношением:
Для подавляющего большинства прозрачных веществ величина μ ≈ 1. Поэтому можно считать, что выполняется:
Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n будет более оптически плотной. Длины волн видимого света в вакууме заключены в пределах:
В веществе длины волн будут другими. В случае колебаний с частотой ν длина волны света в вакууме равна:
Используя соотношение (4.1.49), имеем для длины света в веществе формулу:
Частоты видимого света лежат в пределах:
Модуль среднего по времени потока энергии, переносимого волной, называется интенсивностью света I в данной точке пространства. Интенсивность пропорциональна квадрату амплитуды волны:
Световая волна, как и другие электромагнитные волны, является поперечной, т.е. направления колебаний электрического и магнитного векторов перпендикулярны к направлению ее распространения. В естественном свете присутствуют все направления колебаний электрического и магнитного векторов. Если в волне присутствуют колебания электрического вектора только в одной плоскости (а магнитного вектора в перпендикулярной плоскости), такую волну называют плоскополяризованной (линейно поляризованной) . Есть и более сложные случаи поляризации волн — круговая и эллиптическая. В случае круговой поляризации электрический и магнитный векторы вращаются по кругу с частотой изменения волны. 4.1.5. Геометрическая оптикаДлины воспринимаемых глазом световых волн очень малы (∼10 -7 м), поэтому распространение видимого света в первом приближении можно рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых прямых линий, называемых лучами. В предельном случае, когда длина волны света λ→0, законы оптики можно сформулировать на языке геометрии. Основу геометрической оптики составляют 4 закона:
Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно . Этот закон является приближенным: при прохождении света через очень малые отверстия, размеры которых сравнимы с диной волны света, наблюдается отклонение от прямолинейности, тем большее, чем меньше отверстие. Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга . Это означает, что пересечение лучей не мешает каждому из них распространяться независимо друг от друга. Этот закон справедлив при не слишком больших интенсивностях световых волн. В основу геометрической оптики был положен принцип Ферма : свет распространяется по такому пути, для прохождения которого ему требуется минимальное время . Пусть для прохождения участка ds свету требуется время dt = ds/v, где v — скорость света в данной точке среды. Поскольку v = c/n, то получим:
Следовательно, время τ, необходимое для прохождения пути от точки 1 до точки 2 (Рис. 4.1.2), равно:
Рис. 4.1.2. К принципу Ферма Имеющая размерность длины величина
называется оптической длиной пути . В однородной среде оптическая длина пути равна произведению геометрической длины пути на показатель преломления:
Следовательно,
Пропорциональность времени прохождения оптической длине пути дает возможность сформулировать принцип Ферма так: свет распространяется по такому пути, оптическая длина которого минимальна. Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален при движении света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении. Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (Рис. 4.1.3). Рис. 4.1.3. Закон отражения света как следствие принципа Ферма Прямой путь из А в В прегражден экраном Э. Среда, в которой распространяется луч, однородна, поэтому минимальность оптической длины пути сводится к минимальности геометрической длины пути. Геометрическая длина произвольно взятого пути равна АО’B = A’O’B, поскольку вспомогательная точка A’ является зеркальным отражением точки А, и АО’ = A’O’. Из Рис. 4.1.3 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. При удалении точки O’ от точки О геометрическая длина пути неограниченно возрастает, что противоречит принципу Ферма. Этот результат можно записать так:
Соотношение (4.1.62) выражает закон отражения света : отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения. Найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была минимальной (Рис. 4.1.4). Рис. 4.1.4. К расчету закона преломления света из принципа Ферма Для произвольного луча оптическая длина пути равна:
Чтобы найти минимальное значение оптической длины пути, продифференцируем L по х и приравняем производную к нулю:
Множители при n1 и n2 равны, соответственно, sinθ и sinθ». Поэтому получаем соотношение:
которое выражает закон преломления света. Используя взаимосвязь показателей преломления с фазовыми скоростями распространения света в средах, можно записать соотношение (4.1.65) в виде:
Следовательно, закон преломления света гласит: преломленный луч лежит в одной плоскости с падающим лучом и нормалью; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ. В (4.1.66) n12 — относительный показатель преломления второго вещества по отношению к первому. Из (4.1.65) видно, что при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нормали к поверхности раздела сред. Увеличение угла падения сопровождается более быстрым ростом угла преломления, и при достижении некоторого предельного угла падения угол преломления будет равным 90°:
Отсюда:
При углах падения, лежащих в пределах от θпред пред до 90°, преломленной волны не существует, вся энергия падающей волны переходит в энергию отраженной волны. Это явление называется полным внутренним отражением.
Во многих оптических приборах для преломления света используются стеклянные призмы. На Рис. 4.1.5 показан ход луча монохроматического света в призме. Рис. 4.1.5. Ход лучей в призме После двукратного преломления луч оказывается отклоненным от первоначального положения на угол δ ( угол отклонения ). Угол θ, заключенный между преломляющими гранями, называется преломляющим углом . Угол δ зависит от преломляющего угла θ и показателя преломления призмы. Эта зависимость может быть легко показана для призмы с малым преломляющим углом θ (тонкой призмы) в случае малого угла падения α. Исходя из закона преломления и принимая значение показателя преломления воздуха равным единице, можно записать:
При малых углах α и θ углы α1, γ и γ1 также малы. Поэтому вместо (4.1.69) можно приближенно записать:
Из четырехугольника BQDE, в котором углы при В и D — прямые, найдем, что угол BED равен 180° — θ. Тогда из четырехугольника BСDE находим:
Отсюда
Угол δ из треугольника BED равен:
Подставляя в (4.1.72) результаты (4.1.73) и (4.1.70), получим окончательно:
4.1.6. Преломление в линзеВ практических применениях большое значение имеет преломление света на сферической границе раздела двух сред. Основная деталь оптических приборов — линза — обычно представляет собой стеклянное тело, ограниченное с двух сторон сферическими поверхностями. В частном случае одна из поверхностей линзы может быть плоской. Такую поверхность можно рассматривать как сферическую с бесконечно большим радиусом кривизны. Линзы могут быть изготовлены не только из стекла, а из любого прозрачного вещества с показателем преломления, превышающим единицу, например, из кварца, каменной соли, пластмасс и других материалов. Поверхности линз могут быть и более сложной формы — цилиндрические, параболические и т.д. Рассмотрим линзу, ограниченную двумя сферическими преломляющими поверхностями PO1Q и PO2Q (Рис. 4.1.6). Рис. 4.1.6. Тонкая линза Центр первой преломляющей поверхности PO1Q лежит в точке С1, центр второй поверхности PO2Q — в точке С2. Будем считать, что расстояние O1O2 мало по сравнению с O1С1 или O2С2. В таком случае точки O1 и O2 можно считать практически совпадающими с точкой О — оптического центра линзы. Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью , остальные — побочными осями . Луч, идущий по какой-либо оптической оси, проходя через тонкую линзу, не меняет своего направления. Лучи, идущие параллельно главной оптической оси, после преломления в линзе пересекаются в одной точке F, расположенной на главной оптической оси и называемой главным фокусом . Покажем, что лучи, исходящие под небольшими углами α из некоторой точки А, лежащей на главной оптической оси, собираются линзой в одну точку А1, расположенную также на этой оптической оси и называемую изображением точки А (Рис. 4.1.7). Рис. 4.1.7. Преломление в тонкой линзе Построим плоскости, касательные к поверхностям линзы в точках М и N (в местах падения луча на линзу и его выхода из линзы), и проведем в эти точки радиусы R1 и R2 кривизны поверхностей линзы. Тогда луч AMNA1 можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α1, β1 и толщины линзы, можно записать:
где а и b — расстояния от источника света А и от его изображения А1 до оптического центра линзы. Из треугольников АНА1 и ВЕВ1 следует, что:
Принимая во внимание формулы (4.1.75), получим:
Учтено, что для тонкой линзы h1 ≈ h2 ≈ h. Поскольку, согласно формуле (4.1.74) для тонкой призмы выполняется: θ = (n-1)δ, то, с помощью (4.1.77) имеем формулу линзы :
В эту формулу не входит величина h, что означает, что расстояние b не зависит от от положения точки М. Следовательно, все лучи, исходящие из точки А, соберутся после преломления разными частями линзы в одной точке А1 . Если точка А находится бесконечно далеко от линзы (а = ∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то, согласно формуле (4.1.78), имеем:
Величина b = f называется фокусным расстоянием линзы :
Фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси. Принимая во внимание (4.1.80), формулу линзы (4.1.78) можно сейчас переписать так:
Величина, обратная фокусному расстоянию, называется оптической силой линзы :
Оптическая сила выражается в диоптриях (дп). 1 дп — оптическая сила линзы с фокусным расстоянием в 1 м. 4.1.7. Принцип ГюйгенсаВ приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. В действительности световая волна распространяется во всем пространстве за преградой, проникая проникать в область геометрической тени, причем это проникновение будет тем более существенным, чем меньше размеры отверстия. При диаметре отверстия или ширине щели, сравнимых с длиной волны, приближение геометрической оптики становится совершенно неприменимым. Качественно поведение света за преградой с отверстием может быть объяснено с помощью принципа Гюйгенса . Согласно принципу Гюйгенса каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времени. Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (Рис. 4.1.8). Рис. 4.1.8. К принципу Гюйгенса Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды. 4.1.8. Интерференция световых волнЕсли в среде распространяются одновременно несколько электромагнитных волн, то волны просто накладываются друг на друга, не возмущая одна другую. Это утверждение, подкрепленное опытом, называется принципом суперпозиции. В случае, когда колебания электрического и магнитного векторов в каждой из волн происходят так, что между соответственными векторами в разных волнах имеется постоянный во времени и в пространстве фазовый сдвиг, такие волны называются когерентными . Очевидно, что условие когерентности может существовать лишь для волн, которые имеют одинаковые частоты и, соответственно, длины волны. При сложении когерентных волн возникает явление интерференции , заключающееся в том, что электромагнитные волны в одних точках пространства усиливают, а в других ослабляют друг друга. Пусть две волны одинаковой частоты, распространяющиеся в одном направлении, возбуждают в некоторой точке пространства колебания:
Эти векторы можно представить как вращающиеся с частотой ω вокруг общего начала коор-динат. Поскольку сдвиг фаз различен, в какой-либо момент времени эти вектора займут различные положения (Рис. 4.1.9). Рис. 4.1.9. К расчету интерференции волн Используя теорему косинусов, получим амплитуду результирующего колебания:
Если сдвиг фаз между когерентными колебаниями равен нулю (волны — в фазе), то амплитуда результирующей волны максимальна и равна A = A1 + A2. Пусть амплитуды этих волн равны. В этом случае имеем амплитуду результирующей волны:
Если сдвиг фаз между когерентными колебаниями равен ±π (волны — в противофазе), то амплитуда результирующей волны минимальна и равна A = A1 — A2. Если амплитуды этих волн равны, то в этом случае они гасят друг друга:
Когерентные световые волны можно получить, разделив, например, с помощью зеркал волну, излучаемую одним источником, на две. Если заставить эти волны пройти разные пути, а затем наложить их друг на друга, будет наблюдаться интерференция. Пусть такое разделение происходит в точке О (Рис. 4.1.10). Рис. 4.1.10. Образование когерентных волн До точки Р первая волна пройдет в среде с показателем преломления n1 путь S1, вторая волна пройдет в среде с показателем преломления n2 путь S2. Если в точке О фаза колебания была равна ωt, то первая волна возбудит в точке Р колебание
а вторая волна — колебание
поскольку фазовые скорости волн в средах равны, соответственно: . Следовательно, разность фаз волн в точке Р будет равна:
Поскольку выполняется:
то, подставляя (4.1.90) в (4.1.8), для сдвига фаз имеем выражение:
где
есть величина, называемая оптической разностью хода и равная разности оптических длин проходимых волнами путей в средах с различными показателями преломления. Из (4.1.91) следует, что если оптическая разность хода равна целому числу длин волн в вакууме:
то разность фаз оказывается кратной 2π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Следовательно, (4.1.93) является условием интерференционного максимума. Если Δ равна полуцелому числу длин волн в вакууме:
то разность фаз оказывается равной δ = ±(2m + 1)π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (4.1.94) является условием интерференционного минимума. 4.1.9. Дифракция световых волнДифракцией называется совокупность явлений, связанных с отклонениями от законов геометрической оптики. В частности, вследствие дифракции происходит огибание световыми волнами препятствий и проникновение света в область геометрической тени. Между интерференцией и дифракцией нет существенного физического различия. Свет, идущий от небольшого яркого источника через круглое отверстие (Рис. 4.1.11) должен по правилам геометрической оптики дать на экране резко ограниченный светлый кружок на темном фоне. Рис. 4.1.11. Дифракция от круглого отверстия Такая картина наблюдается при обычных условиях опыта. Но если расстояние от отверстия до экрана в несколько тысяч раз превосходит размеры отверстия, то образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец. Интересный случай дифракции осуществляется с помощью дифракционной решетки, которая представляет собой пластинку, на поверхности которой чередуются узкие параллельные прозрачные и непрозрачные полоски. Сумму ширины прозрачной и непрозрачной полосок называют периодом решетки. Пусть на решетку падает монохроматический свет с длиной волны λ (Рис. 4.1.12). Фронт волны параллелен плоскости решетки. Рис. 4.1.12. Дифракционная решетка Разности хода лучей, идущих от соответствующих точек отверстий, например от правых краев (точки А, А1, А2, . ), или от левых краев (точки В, В1, В2, . ) имеют одно и то же значение: Для того, чтобы все пучки усиливали друг друга, необходимо, чтобы разность хода равнялась целому числу длин волн:
где m — целое число. Это условие позволяет определить те значения углов φ и соответствующие направления, в которых будут наблюдаться максимумы света длины волны λ. Для данной длины волны может наблюдаться несколько максимумов. Направление, соответствующее m = 0, есть φ = 0. Это — направление первоначального пучка. Соответствущий максимум носит название максимума нулевого порядка. При m = 1 имеем: sinφ1 = λ/d, при m = 1 имеем: sinφ’1 = λ/d, т.е. имеется два максимума первого порядка, расположенных симметрично по обеим сторонам от нулевого максимума. Аналогично располагаются максимумы второго, третьего и т.д. порядков. Отсюда следует, что для волн разной длины λ положения максимумов нулевого порядка совпадают , а положения максимумов первого, второго и т.д. порядков различны: чем больше λ, тем больше соответствующие углы. Если на решетку падает белый свет, то в плоскости экрана получается ряд цветных изображений щели. На месте нулевого максимума будет изображение щели в белом свете, а по обе стороны от него развернутся цветные полосы от фиолетового к красному концу. Чем больше общий размер решетки, т.е. чем больше полосок она содержит, тем выше ее качество: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче), и улучшает разрешение близких волн (максимумы становятся резче). Зная период дифракционной решетки, ее можно использовать для определения длины световой волны, измерив величину угла φ, определяющего положение максимума данного порядка. В этом случае имеем:
Измерение длины световой волны с помощью дифракционной решетки принадлежит к числу наиболее точных методов. 4.1.10. Поляризация световых волнПоляризованным называется свет, в котором направления колебаний электрического и магнитного векторов упорядочены каким-либо образом. В естественном свете колебания происходят в различных направлениях, быстро и беспорядочно сменяя друг друга. Различают свет эллиптически поляризованный, поляризованный по кругу, плоскополяризованный. В случае эллиптической или круговой поляризаций электрический и магнитный векторы вращаются в пространстве с частотой, равной частоте волны, причем концы этих векторов описывают либо эллипс, либо круг. Вращение может происходить как по, так и против часовой стрелки. Если вектор вращается в пространстве как правый винт, то поляризацию называют правой, и левой — если вектор вращается в пространстве как левый винт. Важный частный случай — плоская поляризация. В этом случае вектор электрического поля колеблется в плоскости, проходящей через направление распространения волны и этот вектор. Такую плоскость называют плоскостью колебаний . Вектор магнитного поля колеблется в плоскости, также проходящей через направление распространения волны и этот вектор, но данная плоскость — плоскость поляризации — составляет с плоскостью колебаний прямой угол (Рис. 4.1.13). Рис. 4.1.13. Структура плоскополяризованной световой волны Плоскополяризованный свет можно получить из естественного с помощью устройств, которые называются поляризаторами . Эти устройства свободно пропускают волны с колебаниями, плоскость которых совпадает с плоскостью пропускания поляризатора, и задерживают все другие волны. Пусть на поляризатор падает плоскополяризованный свет амплитуды А0 и интенсивности I0. Сквозь устройство пройдет составляющая колебания с амплитудой А|| = А0cosφ, где угол φ — угол между плоскостью колебаний падающего света и плоскостью пропускания поляризатора (Рис. 4.1.14). Рис. 4.1.14. Прохождение плоскополяризованного света через поляризатор Следовательно, интенсивность прошедшего света определяется выражением:
Это соотношение носит название закона Малюса. Пусть на пути естественного луча стоят два поляризатора, плоскости пропускания которых составляют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого I0 составит половину интенсивности естественного неполяризованного света Iест. Используя закон Малюса, получаем:
Максимальная интенсивность получается при φ = 0 (плоскости пропускания поляризаторов параллельны). При φ = 90° интенсивность равна нулю — скрещенные поляризаторы не пропускают свет. 4.1.11. Вращение плоскости |
| (4.1.99) |
где α — постоянная оптического вращения, различная для разных веществ.
В растворах угол поворота плоскости поляризации пропорционален пути l, пройденному светом в растворе и концентрации с активного вещества:
| (4.1.100) |
Здесь [α] — удельная постоянная вращения.
В зависимости от направления вращения вещества подразделяются на право- и левовращающие. Существуют правый и левый кварц, правый и левый сахар и т.д. Молекулы или кристаллы одной модификации являются зеркальным отражением молекул или кристаллов другой модификации.
Если между двумя скрещенными поляризаторами поместить оптически активное вещество, то поле зрения просветляется. Чтобы снова затемнить его, надо повернуть один из поляризаторов на угол, определяемый соотношениями (4.1.99) или (4.11.100). Таким методом можно измерить концентрацию активного вещества в растворе, в частности, концентрацию сахара.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
http://www.kgau.ru/distance/2013/et4/001/04_01.htm

 407. Два прямолинейных бесконечно длинных проводника с токами расположены перпендикулярно друг к другу и находятся в одной плоскости. Определить индукцию магнитного поля в точках М1 и М2, если токи I1=2 А, I2=3 А. Расстояния АМ1 =АМ2 =1 см, ВМ1 =СМ2 =2 см.
407. Два прямолинейных бесконечно длинных проводника с токами расположены перпендикулярно друг к другу и находятся в одной плоскости. Определить индукцию магнитного поля в точках М1 и М2, если токи I1=2 А, I2=3 А. Расстояния АМ1 =АМ2 =1 см, ВМ1 =СМ2 =2 см. 409. По проводу, согнутому в виде правильного шестиугольника со стороной а=20 см, течёт ток I=100 А. Определить индукцию магнитного поля в центре шестиугольника. Для сравнения определить магнитную индукцию магнитного поля в центре кругового провода, совпадающего с окружностью, описанной около данного шестиугольника.
409. По проводу, согнутому в виде правильного шестиугольника со стороной а=20 см, течёт ток I=100 А. Определить индукцию магнитного поля в центре шестиугольника. Для сравнения определить магнитную индукцию магнитного поля в центре кругового провода, совпадающего с окружностью, описанной около данного шестиугольника.