Задачи по дифференциальным уравнениям с разделяющимися переменными

Например, \(при U_0=5В,\ RC=0,01 с\) график разрядки конденсатора имеет вид:

Дифференциальные уравнения с разделяющимися переменными

В целом ряде обыкновенных ДУ 1 -го порядка существуют такие, в которых переменные х и у можно разнести в правую и левую части записи уравнения. Переменные могут быть уже разделены, как это можно видеть в уравнении f ( y ) d y = g ( x ) d x . Разделить переменные в ОДУ f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x можно путем проведения преобразований. Чаще всего для получения уравнений с разделяющимися переменными применяется метод введения новых переменных.

В этой теме мы подробно разберем метод решения уравнений с разделенными переменными. Рассмотрим уравнения с разделяющимися переменными и ДУ, которые можно свести к уравнениям с разделяющимися переменными. В разделе мы разобрали большое количество задач по теме с подробным разбором решения.

Для того, чтобы облегчить себе усвоение темы, рекомендуем ознакомиться с информацией, которая размещена на странице «Основные определения и понятия теории дифференциальных уравнений».

Дифференциальные уравнения с разделенными переменными f ( y ) d y = g ( x ) d x

Уравнениями с разделенными переменными называют ДУ вида f ( y ) d y = g ( x ) d x . Как следует из названия, переменные, входящие в состав выражения, находятся по обе стороны от знака равенства.

Договоримся, что функции f ( y ) и g ( x ) мы будем считать непрерывными.

Для уравнений с разделенными переменными общий интеграл будет иметь вид ∫ f ( y ) d y = ∫ g ( x ) d x . Общее решение ДУ в виде неявно заданной функции Ф ( x , y ) = 0 мы можем получить при условии, что интегралы из приведенного равенства выражаются в элементарных функциях. В ряде случаев выразить функцию у получается и в явном виде.

Найдите общее решение дифференциального уравнения с разделенными переменными y 2 3 d y = sin x d x .

Проинтегрируем обе части равенства:

∫ y 2 3 d y = ∫ sin x d x

Это, по сути, и есть общее решение данного ДУ. Фактически, мы свели задачу нахождения общего решения ДУ к задаче нахождения неопределенных интегралов.

Теперь мы можем использовать таблицу первообразных для того, чтобы взять интегралы, которые выражаются в элементарных функциях:

∫ y 2 3 d y = 3 5 y 5 3 + C 1 ∫ sin x d x = — cos x + C 2 ⇒ ∫ y 2 3 d y = ∫ sin x d x ⇔ 3 5 y 3 5 + C 1 = — cos x + C 2
где С 1 и С 2 – произвольные постоянные.

Функция 3 5 y 3 5 + C 1 = — cos x + C 2 задана неявно. Она является общим решением исходного дифференциального уравнения с разделенными переменными. Мы получили ответ и можем не продолжать решение. Однако в рассматриваемом примере искомую функцию можно выразить через аргумент х явно.

3 5 y 5 3 + C 1 ⇒ y = — 5 3 cos x + C 3 5 , где C = 5 3 ( C 2 — C 1 )

Общим решением данного ДУ является функция y = — 5 3 cos x + C 3 5

Ответ:

Мы можем записать ответ несколькими способами: ∫ y 2 3 d y = ∫ sin x d x или 3 5 y 5 3 + C 1 = — cos x + C 2 , или y = — 5 3 cos x + C 3 5

Всегда стоит давать понять преподавателю, что вы наряду с навыками решения дифференциальных уравнений также располагаете умением преобразовывать выражения и брать интегралы. Сделать это просто. Достаточно дать окончательный ответ в виде явной функции или неявно заданной функции Ф ( x , y ) = 0 .

Дифференциальные уравнения с разделяющимися переменными f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x

y ‘ = d y d x в тех случаях, когда у является функцией аргумента х .

В ДУ f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x ) d x мы можем провести преобразования таким образом, чтобы разделить переменные. Этот вид ДУ носит название ДУ с разделяющимися переменными. Запись соответствующего ДУ с разделенными переменными будет иметь вид f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x .

Разделяя переменные, необходимо проводить все преобразования внимательно для того, чтобы избежать ошибок. Полученное и исходное уравнения должны быть эквивалентны друг другу. В качестве проверки можно использовать условие, по которому f 2 ( y ) и g 1 ( x ) не должны обращаться в ноль на интервале интегрирования. Если это условие не выполняется, то есть вероятность, что ы потеряем часть решений.

Найти все решения дифференциального уравнения y ‘ = y · ( x 2 + e x ) .

Мы можем разделить х и у , следовательно, мы имеем дело с ДУ с разделяющимися переменными.

y ‘ = y · ( x 2 + e x ) ⇔ d y d x = y · ( x 2 + e x ) ⇔ d y y = ( x 2 + e x ) d x п р и y ≠ 0

При у = 0 исходное уравнение обращается в тождество: 0 ‘ = 0 · ( x 2 + e x ) ⇔ 0 ≡ 0 . Это позволят нам утверждать, что у = 0 является решением ДУ. Это решение мы могли не учесть при проведении преобразований.

Выполним интегрирование ДУ с разделенными переменными d y y = ( x 2 + e x ) d x :
∫ d y y = ∫ ( x 2 + e x ) d x ∫ d y y = ln y + C 1 ∫ ( x 2 + e x ) d x = x 3 3 + e x + C 2 ⇒ ln y + C 1 = x 3 3 + e x + C 2 ⇒ ln y = x 3 3 + e x + C

Проводя преобразование, мы выполнили замену C 2 — C 1 на С . Решение ДУ имеет вид неявно заданной функции ln y = x 3 3 + e x + C . Эту функцию мы в состоянии выразить явно. Для этого проведем потенцирование полученного равенства:

ln y = x 3 3 + e x + C ⇔ e ln y = e x 3 3 + e x + C ⇔ y = e x 3 3 + e x + C

Ответ: y = e x 3 3 + e x + C , y = 0

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными y ‘ = f ( a x + b y ) , a ≠ 0 , b ≠ 0

Для того, чтобы привести обыкновенное ДУ 1 -го порядка y ‘ = f ( a x + b y ) , a ≠ 0 , b ≠ 0 , к уравнению с разделяющимися переменными, необходимо ввести новую переменную z = a x + b y , где z представляет собой функцию аргумента x .

z = a x + b y ⇔ y = 1 b ( z — a x ) ⇒ y ‘ = 1 b ( z ‘ — a ) f ( a x + b y ) = f ( z )

Проводим подстановку и необходимые преобразования:

y ‘ = f ( a x + b y ) ⇔ 1 b ( z ‘ — a ) = f ( z ) ⇔ z ‘ = b f ( z ) + a ⇔ d z b f ( z ) + a = d x , b f ( z ) + a ≠ 0

Найдите общее решение дифференциального уравнения y ‘ = 1 ln ( 2 x + y ) — 2 и частное решение, удовлетворяющее начальному условию y ( 0 ) = e .

Введем переменную z = 2 x + y , получаем:

y = z — 2 x ⇒ y ‘ = z ‘ — 2 ln ( 2 x + y ) = ln z

Результат, который мы получили, подставляем в исходное выражение, проводим преобразование его в ДУ с разделяющимися переменными:

y ‘ = 1 ln ( 2 x + y ) — 2 ⇔ z ‘ — 2 = 1 ln z — 2 ⇔ d z d x = 1 ln z

Проинтегрируем обе части уравнения после разделения переменных:

d z d z = 1 ln z ⇔ ln z d z = d x ⇔ ∫ ln z d z = ∫ d x

Применим метод интегрирования по частям для нахождения интеграла, расположенного в левой части записи уравнения. Интеграл правой части посмотрим в таблице.

∫ ln z d z = u = ln z , d v = d z d u = d z z , v = z = z · ln z — ∫ z d z z = = z · ln z — z + C 1 = z · ( ln z — 1 ) + C 1 ∫ d x = x + C 2

Мы можем утверждать, что z · ( ln z — 1 ) + C 1 = x + C 2 . Теперь, если мы примем, что C = C 2 — C 1 и проведем обратную замену z = 2 x + y , то получим общее решение дифференциального уравнения в виде неявно заданной функции:

( 2 x + y ) · ( ln ( 2 x + y ) — 1 ) = x + C

Теперь примемся за нахождение частного решения, которое должно удовлетворять начальному условию y ( 0 ) = e . Проведем подстановку x = 0 и y ( 0 ) = e в общее решение ДУ и найдем значение константы С .

( 2 · 0 + e ) · ( ln ( 2 · 0 + e ) — 1 ) = 0 + C e · ( ln e — 1 ) = C C = 0

Получаем частное решение:

( 2 x + y ) · ( ln ( 2 x + y ) — 1 ) = x

Так как в условии задачи не был задан интервал, на котором необходимо найти общее решение ДУ, то мы ищем такое решение, которое подходит для всех значений аргумента х , при которых исходное ДУ имеет смысл.

В нашем случае ДУ имеет смысл при ln ( 2 x + y ) ≠ 0 , 2 x + y > 0

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными y ‘ = f x y или y ‘ = f y x

Мы можем свести ДУ вида y ‘ = f x y или y ‘ = f y x к дифференциальным уравнениям с разделяющимися переменными путем выполнения замены z = x y или z = y x , где z – функция аргумента x .

Если z = x y , то y = x z и по правилу дифференцирования дроби:

y ‘ = x y ‘ = x ‘ · z — x · z ‘ z 2 = z — x · z ‘ z 2

В этом случае уравнения примут вид z — x · z ‘ z 2 = f ( z ) или z — x · z ‘ z 2 = f 1 z

Если принять z = y x , то y = x ⋅ z и по правилу производной произведения y ‘ = ( x z ) ‘ = x ‘ z + x z ‘ = z + x z ‘ . В этом случае уравнения сведутся к z + x z ‘ = f 1 z или z + x z ‘ = f ( z ) .

Решите дифференциальное уравнение y ‘ = 1 e y x — y x + y x

Примем z = y x , тогда y = x z ⇒ y ‘ = z + x z ‘ . Подставим в исходное уравнение:

y ‘ = 1 e y x — y x + y x ⇔ z + x z ‘ = 1 e z — z + z ⇔ x · d z d x = 1 e z — z ⇔ ( e z — z ) d z = d x x

Проведем интегрирование уравнения с разделенными переменными, которое мы получили при проведении преобразований:

∫ ( e z — z ) d z = ∫ d x x e z — z 2 2 + C 1 = ln x + C 2 e z — z 2 2 = ln x + C , C = C 2 — C 1

Выполним обратную замену для того, чтобы получить общее решение исходного ДУ в виде функции, заданной неявно:

e y x — 1 2 · y 2 x 2 = ln x + C

А теперь остановимся на ДУ, которые имеют вид:

y ‘ = a 0 y n + a 1 y n — 1 x + a 2 y n — 2 x 2 + . . . + a n x n b 0 y n + b 1 y n — 1 x + b 2 y n — 2 x 2 + . . . + b n x n

Разделив числитель и знаменатель дроби, расположенной в правой части записи, на y n или x n , мы можем привести исходное ДУ в виду y ‘ = f x y или y ‘ = f y x

Найти общее решение дифференциального уравнения y ‘ = y 2 — x 2 2 x y

В этом уравнении х и у отличны от 0 . Это позволяет нам разделить числитель и знаменатель дроби, расположенной в правой части записи на x 2 :

y ‘ = y 2 — x 2 2 x y ⇒ y ‘ = y 2 x 2 — 1 2 y x

Если мы введем новую переменную z = y x , то получим y = x z ⇒ y ‘ = z + x z ‘ .

Теперь нам необходимо осуществить подстановку в исходное уравнение:

y ‘ = y 2 x 2 — 1 2 y x ⇔ z ‘ x + z = z 2 — 1 2 z ⇔ z ‘ x = z 2 — 1 2 z — z ⇔ z ‘ x = z 2 — 1 — 2 z 2 2 z ⇔ d z d x x = — z 2 + 1 2 z ⇔ 2 z d z z 2 + 1 = — d x x

Так мы пришли к ДУ с разделенными переменными. Найдем его решение:

∫ 2 z d z z 2 + 1 = — ∫ d x x ∫ 2 z d z z 2 + 1 = ∫ d ( z 2 + 1 ) z 2 + 1 = ln z 2 + 1 + C 1 — ∫ d x x = — ln x + C 2 ⇒ ln z 2 + 1 + C 1 = — ln x + C 2

Для этого уравнения мы можем получить решение в явном виде. Для этого примем — ln C = C 2 — C 1 и применим свойства логарифма:

ln z 2 + 1 = — ln x + C 2 — C 1 ⇔ ln z 2 + 1 = — ln x — ln C ⇔ ln z 2 + 1 = — ln C x ⇔ ln z 2 + 1 = ln C x — 1 ⇔ e ln z 2 + 1 = e ln 1 C x ⇔ z 2 + 1 = 1 C x ⇔ z ± 1 C x — 1

Теперь выполним обратную замену y = x ⋅ z и запишем общее решение исходного ДУ:

y = ± x · 1 C x — 1

В даном случае правильным будет и второй вариант решения. Мы можем использовать замену z = x y Рассмотрим этот вариант более подробно.

Выполним деление числителя и знаменателя дроби, расположенной в правой части записи уравнения на y 2 :

y ‘ = y 2 — x 2 2 x y ⇔ y ‘ = 1 — x 2 y 2 2 x y

Тогда y ‘ = 1 — x 2 y 2 2 x y ⇔ z — z ‘ x z 2 = 1 — z 2 2 z

Проведем подстановку в исходное уравнение для того, чтобы получить ДУ с разделяющимися переменными:

y ‘ = 1 — x 2 y 2 2 x y ⇔ z — z ‘ x z 2 = 1 — z 2 2 z

Разделив переменные, мы получаем равенство d z z ( z 2 + 1 ) = d x 2 x , которое можем проинтегрировать:

∫ d z z ( z 2 + 1 ) = ∫ d x 2 x

Если мы разложим подынтегральную функцию интеграла ∫ d z z ( z 2 + 1 ) на простейшие дроби, то получим:

∫ 1 z — z z 2 + 1 d z

Выполним интегрирование простейших дробей:

∫ 1 z — z z 2 + 1 d z = ∫ z d z z 2 + 1 = ∫ d t z — 1 2 ∫ d ( z 2 + 1 ) z 2 + 1 = = ln z — 1 2 ln z 2 + 1 + C 1 = ln z z 2 + 1 + C 1

Теперь найдем интеграл ∫ d x 2 x :

∫ d x 2 x = 1 2 ln x + C 2 = ln x + C 2

В итоге получаем ln z z 2 + 1 + C 1 = ln x + C 2 или ln z z 2 + 1 = ln C · x , где ln C = C 2 — C 1 .

Выполним обратную замену z = x y и необходимые преобразования, получим:

y = ± x · 1 C x — 1

Вариант решения, при котором мы выполняли замену z = x y , оказался более трудоемким, чем в случае замены z = y x . Этот вывод будет справедлив для большого количества уравнений вида y ‘ = f x y или y ‘ = f y x . Если выбранный вариант решения подобных уравнений оказывается трудоемким, можно вместо замены z = x y ввести переменную z = y x . На результат это никак не повлияет.

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R

Дифференциальные уравнения y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 можно свести к уравнениям y ‘ = f x y или y ‘ = f y x , следовательно, к уравнениям с разделяющимися переменными. Для этого находится ( x 0 , y 0 ) — решение системы двух линейных однородных уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0 и вводятся новые переменные u = x — x 0 v = y — y 0 . После такой замены уравнение примет вид d v d u = a 1 u + b 1 v a 2 u + b 2 v .

Найти общее решение дифференциального уравнения y ‘ = x + 2 y — 3 x — 1 .

Составляем и решаем систему линейных уравнений:

x + 2 y — 3 = 0 x — 1 = 0 ⇔ x = 1 y = 1

Делаем замену переменных:

u = x — 1 v = y — 1 ⇔ x = u + 1 y = v + 1 ⇒ d x = d u d y = d v

После подстановки в исходное уравнение получаем d y d x = x + 2 y — 3 x — 1 ⇔ d v d u = u + 2 v u . После деления на u числителя и знаменателя правой части имеем d v d u = 1 + 2 v u .

Вводим новую переменную z = v u ⇒ v = z · y ⇒ d v d u = d z d u · u + z , тогда

d v d u = 1 + 2 v u ⇔ d z d u · u + z = 1 + 2 z ⇔ d z 1 + z = d u u ⇒ ∫ d z 1 + z = ∫ d u u ⇔ ln 1 + z + C 1 = ln u + C 2 ⇒ ln 1 + z = ln u + ln C , ln C = C 2 — C 1 ln 1 + z = ln C · u 1 + z = C · u ⇔ z = C · u — 1 ⇔ v u = C · u — 1 ⇔ v = u · ( C · u — 1 )

Возвращаемся к исходным переменным, производя обратную замену u = x — 1 v = y — 1 :
v = u · ( C · u — 1 ) ⇔ y — 1 = ( x — 1 ) · ( C · ( x — 1 ) — 1 ) ⇔ y = C x 2 — ( 2 C + 1 ) · x + C + 2

Это есть общее решение дифференциального уравнения.

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

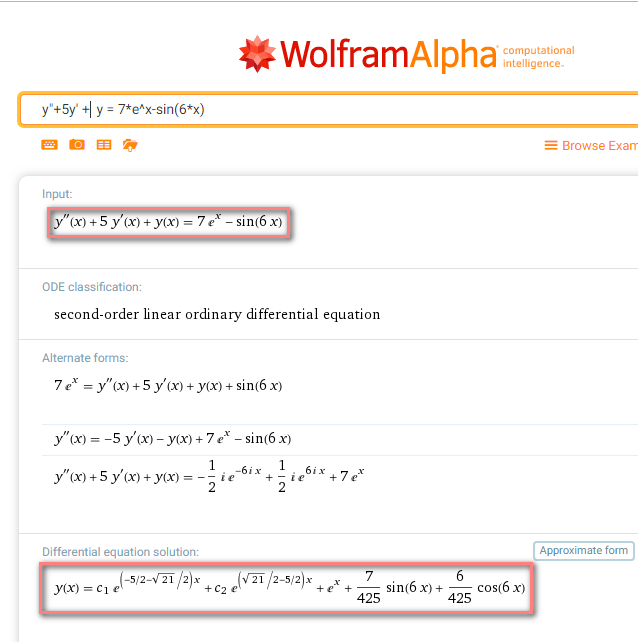
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x \quad (x \ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, \, y(1/3)=1, \, y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= \frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+\cos x, \quad y(0)=0, y'(0)=0, y»(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$