Задачи по экономике дифференциальное уравнение

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016

Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016.

Сборник задач предназначен для студентов высших учебных заведений. обучающихся по экономическим специальностям и изучающим математические дисциплины в соответствии с образовательными стандартами. Приведены разноуровневые экономические задачи, решение которых требует широкомасштабного использования аппарата дифференциальных уравнений. Представлен необходимый теоретический материал, позволяющий решать различные экономические проблемы методами дифференциальных уравнений. Некоторые параграфы содержат необходимый теоретический материал.
Данный задачник будет полезен студентам, аспирантам, преподавателям, а также все и всем желающим научиться применять математический инструментарий в экономических исследованиях и для успешного ведения бизнеса.

Уравнение инфляционного ожидания.
Согласно научным исследованиям на экономические процессы в условиях инфляции заметное влияние может оказывать настроение основной части населения относительно ожидаемого в будущем темпа роста цен. Так, если большая часть населения страны ожидает дальнейшего усиления роста цен, то она не станет вкладывать сбережения в банки, а будет покупать впрок товары повседневного спроса, менять деньги на твердую валюту. т.е. будет себя вести экономически разумно, и в результате темпы роста цен действительно будут увеличиваться.

Если же основная доля населения полагает, что в ближайшем будущем будет оживление в экономике и темпы инфляции снизятся, то люди будут больше покупать товаров длительного пользования и вкладывать деньги в банки (и, тем самым, инвестировать экономику страны), в результате. как правило, такое оживление в экономике действительно наступает.

Оглавление.
Предисловие.
§1. Задачи, приводящие к дифференциальным уравнениям.
1.1. Взаимосвязь функции спроса и эластичности.
1.2. Модель формирования равновесной цены на товар.
1.3. Модель естественного роста.
1.4. Задача об эффективности рекламы.
1.5. Уравнение инфляционного ожидания.
1.6. Задача о доходе и потреблении.
1.7. Закон логистического развития в инновационном менеджменте.
§2. Задачи экономического содержания, решаемые средствами дифференциальных уравнении.
ГЛОССАРИЙ.
Литература.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Задачи экономического содержания и дифференциальные уравнения, Монако Т.П., 2016 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Экономическая задача, приводящая к дифференциальному уравнению

Лекция 3-4

Обыкновенные дифференциальные уравнения

Общее и частные решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения.

Линейные дифференциальные уравнения. Уравнение Бернулли.

Уравнений в полных дифференциалах.

Вопросы

1. Определение обыкновенных дифференциальных уравнений.

2. Дифференциальные уравнения первого порядка.

3. Общее решение дифференциального уравнения.

4. Задачи Коши. Частное решение.

5.Определение дифференциального уравнения 1-ого порядка.

6. Дифференциальные уравнения с разделяющимися переменными.

7. Однородные дифференциальные уравнения.

8. Линейные дифференциальные уравнения первого порядка.

10.Уравнение в полных дифференциалах

Различные вопросы экономики приводят к необходимости решения уравнений, содержащей в качестве неизвестной некоторую функцию и ее производные до определенного порядка n.

Экономическая задача, приводящая к дифференциальному уравнению

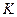
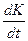
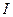
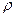
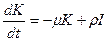
Обозначим — величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная , она выражается через коэффициент выбытия . Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен =1/10. С другой стороны, инвестиции – вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности . Учитывая все это, получим дифференциальное уравнение, вида:

.

Дата добавления: 2015-08-21 ; просмотров: 1125 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Что такое дифференциальное уравнение и зачем оно нужно?

На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.

Дифференциальные уравнения – простейшие виды

Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?

Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.

То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.

Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=\int f(x)dx.$$

Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)\cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$\int \frac=\int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.

Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).

Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.

Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.

Пример применения дифференциального уравнения в экономике

Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.

Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.

Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.

Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.

С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.

Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = \int (10-0,2q)dq = 10 q-0,1q^2+C. $$

Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.

Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.