Задачи решаемые с помощью систем линейных уравнений

Решение задач с помощью систем линейных уравнений. 7-й класс

Разделы: Математика

Класс: 7

Аннотация: Урок объяснения нового материала. На уроке рассматриваются три разных способа решения одной задачи. Тем самым школьники приучаются анализировать условие задачи и выбирать более простой способ решения. Первый опыт применения уравнений для решения текстовых задач у учащихся уже имеется. Различные способы решения систем линейных уравнений уже изучены. И одна из целей урока — показать использование системы уравнений как математической модели реальной ситуации. Использование на уроке технических средств позволяет сделать урок ярким, насыщенным, полным и дает возможность мгновенно осуществить проверку решаемых на уроке заданий. Это очень важно, так как экономится время, а учащиеся, работающие самостоятельно, получают возможность проверить себя и вернуться назад, чтобы устранить свои ошибки. Тем самым осуществляется самоконтроль, внутренняя обратная связь — важнейший фактор самоуправления процесса обучения.

Цели

Решите задачу, составив числовое выражение:

Купили 7 тетрадей по 2р. и 2 ручки по 4р. Сколько денег заплатили?

Турист ехал 2ч на поезде со скоростью 60км/ч и 3ч шел пешком со скоростью 5км/ч. Какое расстояние он преодолел?

Решите задачу, составив буквенное выражение:

Купили 10 тетрадей по Х р и 3 ручки по У р. Сколько заплатили за всю покупку?

Турист ехал 3ч на автобусе со скоростью Х км/ч и 2ч шел пешком со скоростью 4км/ч

Перейдите от словесной модели к математической:

Числа В и С равны

Число А на 18 больше числа В

Число Х в 6 раз меньше числа У

Разность Р и Н на 17 больше их частного

Создайте реальную ситуацию по модели:

I Этап. Объяснение нового материала.

Задача На турбазе имеются палатки и домики. Всего их 25. В каждом домике размещается по 4 человека, в каждой палатке — по 2 человека. Сколько палаток и сколько домиков на турбазе, если на ней отдыхает всего 70 человек?

Решим задачу арифметически.

25*2=50(чел) разместилось бы, если селить по 2

70-50=20(чел) не расселили

20:2=10(домиков), т.к. подселяют еще по 2

Ответ: 10 домиков, 15 палаток.

Решим эту задачу с помощью уравнения.

(Вспомним этапы математического моделирования)

II этап. Составление математической модели.

Пусть на турбазе Х палаток, тогда домиков 25-Х. Т. к. в каждой палатке по 2 человека, то 2Х чел живут в палатках. Т. к. в каждом домике по 4 человека, то 4(25-Х) чел. живут в домиках. Зная, что всего на турбазе 70 чел, составим уравнение:

III этап. Работа с моделью.

IV. этап. Ответ на вопрос задачи: 15 палаток и 10 домиков.

Самый трудный этап в решении задач — составление математической модели. Ученик всегда затрудняется, что удобнее обозначить за Х. Всегда возникает желание обозначить за Х то, о чем спрашивается в задаче. Но в данной задаче два вопроса. Две искомые величины. Можно ли решить эту задачу, введя два неизвестных? Попробуем.

Пусть Х — палаток, а У — домиков. Т. к их всего 25, то Х+У=25. 2Х чел живут в палатках, а 4У чел — в домиках. 2Х+4У=70 Получили два уравнения и оба с двумя незвестными.

Как же их решить? Составить систему двух уравнений с двумя неизвестными и решить ее.

Вспоминаем способы решения систем линейных уравнений.

Решив систему, получаем тот же ответ: 10 домиков, 15 палаток.

Делаем вывод: Система линейных уравнений тоже может быть использована как математическая модель реальной ситуации. Чтобы решить задачу с помощью системы надо ввести два неизвестных и составить два уравнения с ними. Способ решения системы надо выбирать тот, который представляется более уместным, или тот, который больше нравиться. Этапы математического моделирования те же, что и при решении задач с помощью уравнения.

Закрепление изученного материала.

Решите с помощью системы уравнений:

1. У причала находилось 6 лодок, часть из которых была двухместными, а часть — трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и сколько трехместных лодок было у причала?

2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?

Подведение итогов урока.

Домашнее задание: параграф 14 , №14.7, 14.14.

Решение задач с помощью систем линейных уравнений

Алгоритм решения задачи с помощью системы линейных уравнений

1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).

Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.

«От смысла к буквам»:

Пусть x и y — задуманные числа.

Уравнения по условию задачи::

Решение системы уравнений:

«От букв к смыслу»:

Задуманы числа 37 и 27.

Примеры

Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.

Найдите стороны прямоугольника.

Пусть a и b — длина и ширина прямоугольника.

$$ <\left\< \begin P = 2(a+b) = 48 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin a+b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin 3b+b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin 4b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin a = 18 \\ b = 6 \end \right.> $$

Ответ: длина прямоугольника 18 см, ширина 6 см.

Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?

Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.

$$ <\left\< \begin 70x+100y = 100500 |:10 \\ 30x-30y = 5550 |:30 \end \right.> (-) \Rightarrow <\left\< \begin 7x+10y = 10050 \\ x-y=185 | \times 10 \end \right.>$$

$$ \Rightarrow (+) <\left\< \begin 7x+10y = 10050 \\ 10x-10y = 1850 \end \right.> \Rightarrow <\left\< \begin 17x = 11900 \\ y = x-185 \end \right.> \Rightarrow <\left\< \begin x = 700 \\ y = 515 \end \right.> $$

Ответ: 700 строк и 515 строк

Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?

Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.

$$ <\left\< \begin 2x+3y = 1540 \\ 2y-x = 210 | \times 2 \end \right.> \Rightarrow (+) <\left\< \begin 2x+3y = 1540 \\ -2x+4y = 420 \end \right.> \Rightarrow <\left\< \begin 7y = 1960 \\ x = 2y-210 \end \right.> \Rightarrow <\left\< \begin x = 350 \\ y = 280 \end \right.> $$

Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.

Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.

Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).

$$ \Rightarrow <\left\< \begin 5v-u = 73 \\ v+7u = 29 \end \right.> \Rightarrow <\left\< \begin 5(29-7u)-u = 73 \\ v = 29-7u \end \right.> \Rightarrow <\left\< \begin 145-35u-u = 73 \\ v = 29-7u \end \right.> \Rightarrow$$

Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч

Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.

Пусть x – первоначальная цена карандаша, y — тетрадки.

$$ <\left\< \begin 5x+3y = 170 \\ 3\cdot0,8x+5\cdot1,3y = 284 \end \right.> \Rightarrow <\left\< \begin 5x+3y = 170 |\times \frac<2,4> <5>\\ 2,4x+6,5y = 284 \end \right.> \Rightarrow (-) <\left\< \begin 2,4x+1,44y = 81,6 \\ 2,4x+6,5y = 284 \end \right.> $$

Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.

Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.

Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).

Расстояние между А и В неизменно, и по условию равно:

Ответ: обычная скорость 12 км/ч, время 5 ч

Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.

Пусть x — объём первой бочки (л), y – объём второй (л).

Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:

Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:

$$ <\left\< \begin x+ \frac<1> <2>y = 44 | \times 2 \\ \frac<1> <6>x+y = 44 \end \right.> \Rightarrow (-) <\left\< \begin 2x+y = 88 \\ \frac<1> <6>x+y = 44 \end \right.> \Rightarrow (+) <\left\< \begin 1\frac<5> <6>x = 44 \\ y = 88-2x \end \right.> \Rightarrow $$

Ответ: первая бочка 24 л, вторая – 40 л

Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?

Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.

По условию задачи:

Из второго уравнения $ \frac = \frac<0,5> <2>= 0,25 $. Подставляем в первое уравнение:

И тогда искомое время:

$$ t = \frac<2s> = 2\cdot1,25 = 2,5 (ч) $$

Решение задач с помощью систем линейных уравнений

Примеры оформления и образцы решения задач с помощью систем линейных уравнений.

Просмотр содержимого документа
«Решение задач с помощью систем линейных уравнений»

Системы двух линейных уравнений с двумя переменными как математические модели реальных жизненных ситуаций

Множество задач можно решить путем составления систем двух линейных уравнений .

1) построение математической модели ( обозначить через x и y неизвестные величины );

2) составление системы двух уравнений и ее решения; 3) нахождение ответа к задаче.

Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Первый этап . Составляем математическую модель задачи

?, на 30 км/ч быстрее

Обозначим скорость легкового автомобиля – х км/ч, а скорость грузового автомобиля — у км/ч. Оба автомобиля проехали одинаковое расстояние ( S=Vt) .

Составим и решим систему уравнений:

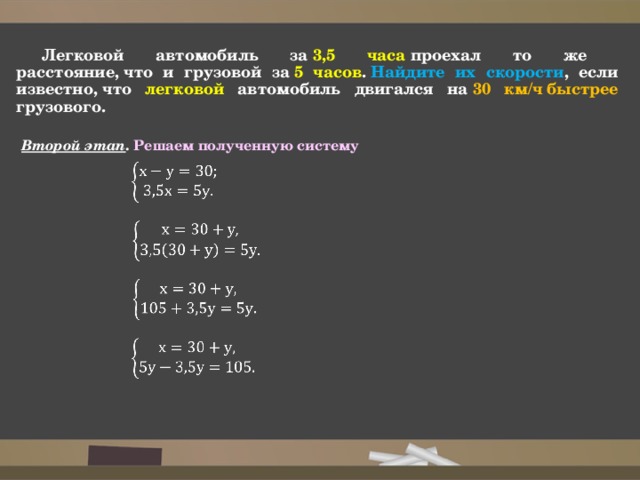
Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Второй этап . Решаем полученную систему

Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Второй этап . Решаем полученную систему

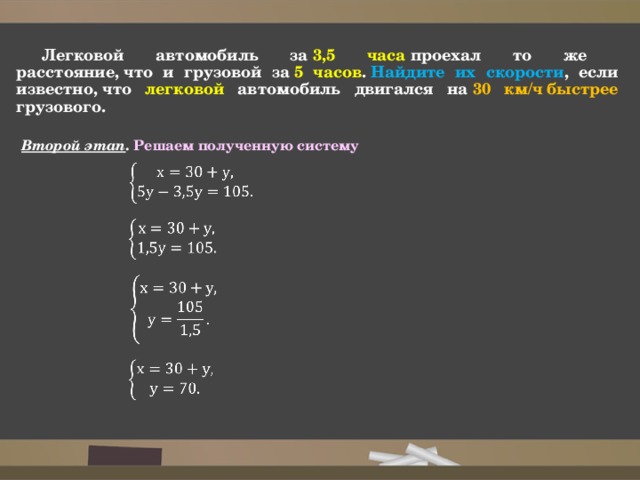
Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

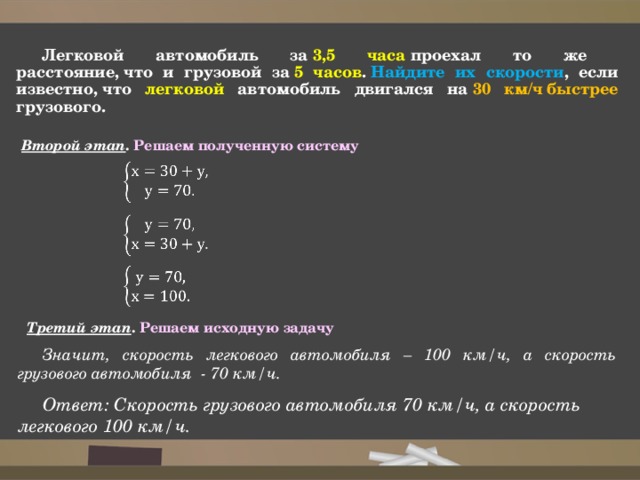
Второй этап . Решаем полученную систему

Значит, скорость легкового автомобиля – 100 км/ч, а скорость грузового автомобиля — 70 км/ч.

Ответ: Скорость грузового автомобиля 70 км/ч, а скорость легкового 100 км/ч.

Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании?

Первый этап . Составляем математическую модель задачи

Итого (смесь 1 и 2 растворов)

Объем раствора, л

Обозначим объем 1 раствора – х, а второго — у. Тогда объем кислоты в первом растворе 0,2х л, а во втором – 0,4у л. Объем кислоты в новом растворе 4  0,325=1,3 л.

Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании?

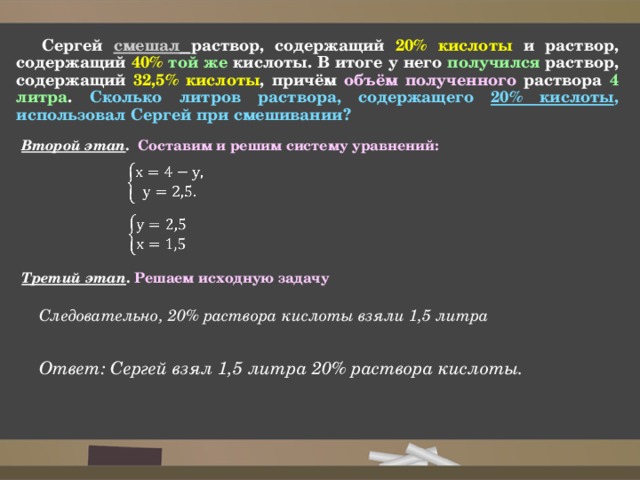
Второй этап . Составим и решим систему уравнений:

Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты , использовал Сергей при смешивании?

Второй этап . Составим и решим систему уравнений:

Следовательно, 20% раствора кислоты взяли 1,5 литра

Ответ: Сергей взял 1,5 литра 20% раствора кислоты.

Иван случайно смешал молоко жирностью 2,5% и молоко жирностью 6% . В итоге у него получилось 5 литров молока жирностью 4,6% . Сколько литров молока жирностью 2,5% было у Ивана до смешивания?

Первый этап . Составляем математическую модель задачи