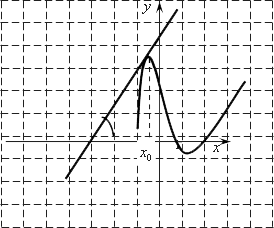Задачи с решением уравнение касательной к графику

Тестовые задания по теме: «Касательная к графику функции»

Разделы: Математика

При изучении темы “Касательная к графику функции” можно выделить 5 типов задач.

I. Задачи на составление уравнения касательной к графику функции в точке, принадлежащей графику

Обучение решению задач на касательную осуществляется при помощи алгоритма.

Уравнение касательной к графику функции y=f(x) в точке х: y = f(х) + f ‘(х)(x – х)

Алгоритм составления уравнения касательной к графику функции y = f(x):

1. Обозначить х абсциссу точки касания.

2. Найти f(х)

3. Найти f ‘(x) и f ‘(х) 4. Подставить найденные числа х, f(х), f ‘(х) в общее уравнение касательной

Задача. Составьте уравнение касательной к графику функции в точке с абсциссой х=3.

1. х = 3 – абсцисса точки касания.

3. f ‘(x) = x 2 – 4, f ‘(3) = 5. 4.Подставив в уравнение касательной значения х=3, f(х)=-2, f ‘(х)=5, получим y = – 2 + 5(x – 3), т.е. y = 5x – 17. Это и есть искомое уравнение касательной. Ответ: y = 5x-17.

Найти уравнение касательной к графику функции f(x) в точке с абсциссой х.

1. f(x)=-x-4x+2, х=-1.	1) y=-2x-3;	2) y=2x-1;	3) y=-2x+3;	4) y=2x+3.
2. f(x)=-x+6x+8, х=-2.	1) y=2x-6;	2 )y=10x+12;	3) y=4x+8;	4) y=-10x+8.
3. f(x)=x+5x+5, х=-1.	1) y=7x+8;	2) y=8x+7;	3) y=9x+8;	4) y=8x+6.
4. f(x)=2cosx, х=	1) y=	2) y=	3) y=	4) y=
5. f(x)=tgx, х= 1) y=x;	2) y=x+	3) y=x-	4) y=x-1.
6. f(x)=1-sin2x, х=0.	1) y=1-2x;	2) y=2x;	3) y = -2x;	4) y=2x+1.
7. f(x)= х=-2.	1) y = -x+1; 2) y = x+1;	3) y = -x-1;	4) y = -x-2.

8. Уравнение касательной, проведённой к графику функции y=lnx в точке его пересечения с осью абсцисс, имеет вид. 1) y = 2x-2; 2) y = x-1; 3) y = x+1; 4) y = x.

9. Уравнение касательной, проведённой к графику функции y=e-1 в точке его пересечения с осью абсцисс, имеет вид. 1) y = 2x; 2) y = 3x-1; 3) y = x-1; 4) y = x.

10. Уравнение касательной, проведённой к графику функции y=sin(x-)+1 в точке его пересечения с осью ординат, имеет вид. 1) y = x+1; 2) y = x-1; 3) y =- x-1; 4) y =1- x.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	3	2	2	2	3	1	3	2	4	4

II. Проведение касательной параллельно заданной прямой

Задача 1. В каких точках касательные к кривой у=— х— х+1 параллельны прямой y=2x-1?

Решение. Так как касательные параллельны прямой у=2х-1 то их угловые коэффициенты совпадают. Т. е. угловой коэффициент касательной в этой точке есть к = 2 .

Находим у’ = х-2х-1; к= у'(х)= х-2х-1=2.

Решив уравнение х-2х-1=2; х-2х-3=0, получим (х)=3, (х)=-1, откуда (у)= -2, (у)= . Итак, искомыми точками касания являются А(3;-2) и В(-1;)

Ответ: (3;-2) и (-1;).

Задача 2. Найти абсциссу точки, в которой касательная к графику функции f(x) = 2x-lnx, параллельна прямой у = х.

Решение. Пусть х— абсцисса точки касания. Угловой коэффициент касательной в этой точке есть к=1. Находим f ‘(x)=2-. К= f ‘ (х)=2-=1.

Решив уравнение 2-=1, получим х=1.

Найти абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у(х).

1. f(x)= х+е, у(х)= -х.	1) —; 2) 0; 3) ; 4) 1.
2. f(x)=2+х, у(х)= 2х.	1) 1; 2) 4; 3) 0; 4) .
3. f(x)=х-5х, у(х)= -х.	1) -2; 2) 3; 3) -3; 4) 2.
4. f(x)=2lnх-x, у(х)= 0.	1) -2; 2) 0; 3) 2; 4) 1.
5. f(x)=-х-е, у(х)= 4-2х.	1) 3; 2) 2; 3) 0; 4) –2.

6. Найти сумму абсцисс точек, в которых касательные к графику функции у=х— 3х+1 параллельны оси абсцисс. 1) 0; 2) 2; 3) 1; 4) –2.

7. Найти сумму абсцисс точек в которых касательные к кривой у= параллельны прямой у=х+5. 1) –2; 2) 4; 3) 2; 4) –4.

8. К графику функции у = проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х= -1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции. 1) –2; 2) 2; 3) 1; 4) –3.

9. К графику функции у =- проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х= 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции. 1) –1; 2) 5; 3) 2; 4) –3.

10. На графике функции у = х (х-4) указать точки, в которых касательные параллельны оси абсцисс. Найти сумму абсцисс данных точек. 1) 5; 2) 4; 3) 3; 4) – 27.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	1	4	2	2	1	4	3	2	1

III. Задачи на касательную, связанные с ее угловым коэффициентом

Задача 1. К графику функции f(x) = 3x+5x-15 в точке с абсциссой x= проведена касательная. Найти тангенс угла наклона касательной к оси Ох.

f'(x) является угловым коэффициентом касательной к графику функции у =f(x) в точке x. Угловой коэффициент прямой равен тангенсу угла, образованного этой прямой с положительным направлением оси Ох.

k= f ‘(x)=tg, где x— абсцисса точки касания, а — угол наклона касательной к оси Ох.

f ‘(x)= f ‘()=6. tg=6.

Задача 2. Напишите уравнение касательной к графику функции f(x) = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0.

Решение. f ‘(x)= x-3. Из условия f ‘(x) = tg 45° найдем x: x – 3 = 1, x= 4.

1. x= 4 – абсцисса точки касания.

2. f(4) = 8 – 12 + 1 = – 3.

4. y = – 3 + 1(x – 4). y = x – 7 – уравнение касательной

Задача 3. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=xlnx в точке x=1.

Решение. k= f'(x)=tg.

Находим f ‘(x)= 2xlnx+x=2xlnx+x=x(2lnx+1).

При x=1 получим f ‘(1)=1, откуда tg=1 и, значит, =.

Ответ: .

К графику функции f(x) в точке с абсциссой x проведена касательная. Найти тангенс угла наклона касательной к оси Ох если:

1. f(x)= 2+x-2x, x=1.	1) -1; 2) –7; 3) 3; 4) 0.
2. f(x)= , x=8.	1) 1; 2) 32; 3) 8; 4) 16.
3. f(x)= 5x-3x-7, x=-1.	1) 21; 2) 14; 3) 9; 4) -21.
4. f(x)= 3x-2lnx, x=2.	1) 10; 2) 8; 3) 11; 4) 11,5.
5. f(x)= -x+14, x=1.	1) -51; 2) –65; 3) 63; 4) 77.

Найти угловой коэффициент касательной проведённой к графику функции f(x) в точке x

6. f(x)=e-x, x=1.	1) e-2; 2) –1; 3) e-1; 4) –2.
7. f(x)=2sinx+2, x=0.	1) -2; 2) 0; 3) 4; 4) 2.
8. f(x)=4cosx-1, x=.	1) 4; 2) 2; 3) -2; 4) 1.
9. f(x)=2+3, x=4.	1) 3,5; 2) 0,5; 3) 7; 4) 2,5.

10. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=3lnx — x, в точке x=1. 1) 2) 3) arctg2; 4)

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	3	1	3	2	1	4	3	2	4

IV. Нахождение касательной проходящей через точку, внешнюю по отношению к заданному графику

Задача 1. Составить уравнения касательных к кривой y = x— 4x+3, проходящих через точку М(2;-5).

При х =2, находим у = 4-8+3=-1-5, то есть точка М не лежит на кривой y = x-4x+3 и не является точкой касания.

Пусть (х) – точка касания.

у ‘ =2х-4, k = 2x— 4. Составим уравнение касательной, проходящей через точку М:

у=-5-(2х-4)(2-х). Поскольку точка (х) лежит на кривой, получим y = x-4x+3.

Решим уравнение x-4x+3 = -5-(2х-4)(2-х);

x-4x+3=2x-8x+3, x— 4x=0, (х)=0, (х)= 4.

Таким образом, получили две точки касания А(0;3) и В(4;3). Итак, существуют две касательные к данной кривой; одна из них имеет угловой коэффициент k= -4 (при х=0) и уравнение у = -4х+3, а другая – угловой коэффициент k=4 (при х=4) и уравнение у=4х-13.

Ответ: у =-4х+3, у = 4х-13.

Через точку М(х;у) проведены две касательные к графику функции f(x). Найти сумму абсцисс точек касания.

1. f(x)=4х-8х-2, М(3;-90).	1) 4; 2) 6; 3) 5; 4) 3.
2. f(x)=7х-2х-5, М(2;-93).	1) 4; 2) 6; 3) 5; 4) 3.
3. f(x)=6х-4х-1, М(1;-23).	1) 1; 2) 5; 3) 2; 4) 3.
4. f(x)=х-8х-2, М(1,5;-54).	1) 2; 2) 4; 3) 5; 4) 3.
5. f(x)=х-9х-5, М(-1,5;4,5).	1) -2; 2) -5; 3) 2; 4) — 3.
6. f(x)=7х-7х-1, М(2;-50).	1) 4; 2) 6; 3) 5; 4) 3.

7. Напишите уравнение касательной к графику функции f(x)= х— 4х + 5, если эта касательная проходит через точку А(0;4) и абсцисса точки касания положительна.

1) у = 2х+4; 2) у = -2х+4; 3) у = -4х+4; 4) у = 4х-3.

8. Напишите уравнение касательной к графику функции f(x)= х+ 3х + 5, если эта касательная проходит через точку А(0;1) и абсцисса точки касания отрицательна.

1) у = 2х+1; 2) у = х+1; 3) у = -х+1; 4) у = -2х-5.

9. Напишите уравнения касательных к графику функции f(x)= -0,5 х+3, если эта касательные проходят через точку на оси Оу и образуют между собой угол 90 o ?.

1) у = х+3,5 и у = х-3,5 ; 2) у = -х+3,5 и у = х+3,5; 3) у = -х+4 и у =х+4; 4) у = -х+3 и у =х+3.

10. Через точку В(-2;3) проходят касательные к графику функции у=. Найти уравнения этих касательных.

1) у = 2х+2 и у = -22х+2; 2) у =-х+3 и у = х-3; 3)у =-0,5х+2 и у =х+4; 4)у =-0,5х+2 и у =-0,1х+2,8.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	1	3	4	4	1	2	4	2	4

V. Нестандартные задачи, связанные с касательной

1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3. Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x₀ = 1, проходит через точку M(2; 3)? Ответ: a = 0,5.

3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2? Ответ: p₁ = – 10, p₂ = 2.

4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16). Ответ: A(2; – 2), B(– 4; 52).

5. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0. Ответ: M(2; 3).

6. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж. Ответ: y = 2x – 4.

7. На параболе y = x 2 взяты две точки с абсциссами x₁ = 1, x₂ = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.

Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.

8. Найдите угол между касательными к графику функции y = x 3 – 4x 2 + 3x + 1, проведенными в точках с абсциссами 0 и 1. Ответ: = 45°.

9. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5. Ответ: y = – 3x и y = x.

10. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.

Ответ: ₁ = arctg 6, ₂ = arctg (– 6).

11. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N. Ответ: K(1; – 9).

12. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15? Ответ: – 1; 31.

13. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.

14. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x₀ = 2, проходит через точку M(1; 8)?

Уравнение касательной и уравнение нормали к графику функции

Как получить уравнение касательной и уравнение нормали

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Решить задачи самостоятельно, а затем посмотреть решения

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Снова решаем задачи вместе

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Задание 6. Касательная к графику функции

Существует целый класс задач 6 из профильного ЕГЭ, в которых вообще не дается график функции. Все, что известно — это уравнение функции и касательной. И сегодня мы будем учиться решать именно такие задачи.

В этой короткой серии уроков мы разберем непростые задачи, которые не так часто встречаются в настоящем ЕГЭ по математике. Однако если встречаются, то у многих учеников вызывают серьезные затруднения. Речь идет о касательных, заданных уравнением, функция которого также задана своим уравнением. Никаких графиков в этих задачах нет. Более того, отдельные два видеоурока будут посвящены примерам, содержащие параметры. И хотя, на первый взгляд, может показаться, что параметры — это очень сложно, на самом деле, такие задания решаются буквально в несколько строчек.

Решаем реальный пример

Итак, первая задача:

Прямая\[y˜=16x-38\]является касательной к графику функции:

Найдите абсциссу точки касания.

Прежде всего, давайте вообще вспомним, что такое касательная к графику функции. Итак, у нас есть некий график, а также прямая, которая касается этого графика, т. е. пересекает график только в одной точке, причем угол ее пересечения с осью $Ox$, точнее, тангенс этого угла равен значению производной в этой точке:

Теперь переведем формальное определение на понятный человеку язык. Во-первых, поскольку наша прямая, заданная уравнением, является касательной, то эти уравнения обязательно имеют общую точку, т. е. они имеют общее решение. Следовательно, мы можем приравнять их правые части, т. е.:

С другой стороны, поскольку речь идет о касательной к графику, а не о произвольной секущей, мы вправе потребовать, чтобы равны были не только сами функции, но еще и их производные, т. е.:

Давайте займемся первым выражением:

Вот мы получили первую конструкцию. Это уравнение третьей степени. Для его решения можно попробовать разложить этот многочлен на множители, и, действительно, после определенных преобразований и нескольких строчек вычислений мы получим несколько кандидатов на ответ. Однако вспомним, что речь идет о простой задаче из ЕГЭ по математике, причем задача из части В. Следовательно, она должна решаться гораздо проще без всяких разложений. И именно для этого нам дано второе уравнение. Мы уже приравняли производные, а теперь давайте посчитаем их:

Мы получили уравнение второй степени. Данное тождество легко решается и через дискриминант, и по формулам Виета. Давайте решим его по формуле Виета:

\[\left( -3 \right)\left( +1 \right)=0\]

Вот мы и получили два корня, это два кандидата на ответ, т. е. те абсциссы, в которых производная нашей касательной к графику функции равна производной. Теперь возвращаемся к нашей исходной конструкции и вспоминаем, что помимо производных сами функции тоже должны быть равны, т. е. из полученных нами иксов нужно выбрать те, которые удовлетворяют уравнению. Давайте подставим\[=3\]:

Очевидно, что\[=3\]является корней обоих выражений — и нашего исходного, и производной. На этом можно было бы закончить решение, но давайте для надежности мы подставим и\[=-1\]:

\[-1-3\cdot 1-9\cdot \left( -1 \right)+27=0\]

Очевидно, что данное выражение не является равенством. Следовательно,\[=-1\]не является корнем нашего тождества. Отсюда заключаем, что единственным корнем, удовлетворяющим все требования, является\[=3\]. Это и является ответом к задаче. Мы нашли абсциссу точки касания к графику.

Ключевые моменты

В заключении давайте еще раз пробежимся по ключевым шагам решения.

В первую очередь, что значит, что прямая является касательной графику функции? Это значит, что данная прямая и $f\left( x \right)$ имеют общее решение. Следовательно, мы можем приравнять $y$ из выражений. Мы получим первое тождество.

Однако после его преобразования, мы получим уравнение третьей степени, а поскольку такая конструкция вообще решается довольно сложно и к тому же имеет несколько корней, мы записываем вспомогательное равенство, вспоминая о том, что речь идет именно о касательных к графику функции, т. е. помимо самих $f\left( x \right)$ равными должны быть еще и их производные. В нашем случае производные легко считаются. Итого у нас получилось простое квадратное равенство, которое затем легко решается, и получается два корня.

Возникает вопрос: какой из этих корней является правильным ответом? Чтобы найти правильный ответ, достаточно каждое из этих чисел подставить в наше уравнение, которое мы получили в самом начале. Здесь мы и получим, что один из корней нас полностью устраивает, а второй корень — нет, т. е. он точно не является решением.

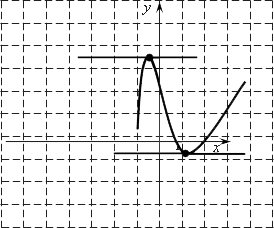
С точки зрения геометрии происходит следующее. Допустим, что у нас есть вот такая функция:

У нее есть точка максимума и точка минимума. В обоих случаях производная равна нулю, и, следовательно, касательная, проведенная через каждую из этих точек, тоже имеет производную, равную 0, т. е. она горизонтальна. Однако, как мы видим, не существует такой касательной к графику функции. Если касательная проходит сверху, то она никак не сможет пересечь кривую в нижнем значении. И, наоборот, если мы рассматриваем касательную в нижней точке, то она никак не сможет пересечь нашу кривую в верхнем значении. Этим и объясняется, что хотя производная функции равна производной касательной в двух точках, в итоге в нашем уравнении нас удовлетворяет лишь одна из них.

Задачи B9 такого типа действительно встречаются на ЕГЭ. Как правило, в процессе решения таких задач возникают целые системы уравнений, которые надо уметь решать. В этом и следующих видеоуроках мы последовательно рассмотрим такие «нестандартные» задачи — от самых простых (как сегодня) до действительно серьезных — с параметром и квадратичной функцией.