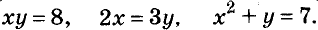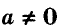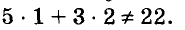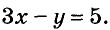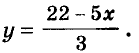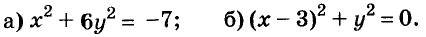Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
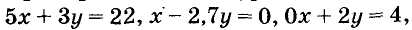
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 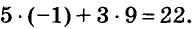
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 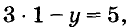
Уравнение 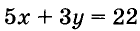
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 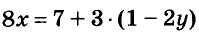
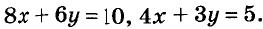
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 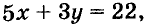
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 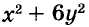
б) Значение выражения 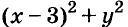
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 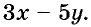
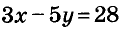
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 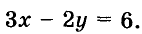
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Решение задач с помощью систем линейных уравнений
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Уравнения по условию задачи::
Решение системы уравнений:
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
$$ <\left\< \begin
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
$$ <\left\< \begin
$$ \Rightarrow (+) <\left\< \begin
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
$$ <\left\< \begin
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
$$ \Rightarrow <\left\< \begin
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
$$ <\left\< \begin
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ <\left\< \begin
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
Из второго уравнения $ \frac
И тогда искомое время:
$$ t = \frac<2s>
Фрагменты уроков по математике «Решение задач, сводящихся к системам линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Приложение 2.ppt
Описание презентации по отдельным слайдам:
Задача 1. Сумма двух чисел равна 63, а их разность равна 12. Найдите эти числа. Первое число Второе число — ? -? — Что нам известно об этих числах? Первое число Первое число Второе число Второе число у у х = 12 = 63 — + х у х
Решим систему уравнений — Каким методом рациональнее решать данную систему уравнений? — Значение х подставим в первое уравнение -Решив эту систему, получим, что х=25,5; у=37,5. Значит, числа равны 25,5 и 37,5. Ответ: первое число равно 37,5; второе число равно 25,5.
Первая встреча Вторая встреча Всего 1300 грамм Всего 800 грамм Сколько грамм самоцветов содержится в каждом мешочке + + = =
— х С малахитом С гранатом — у + + = = 800 грамм 2у у 2х 3х 1300 грамм
Значение х подставим во второе уравнение Решим эту систему методом подстановки. Выразим переменную у из второго уравнения и подставим в первое.
Решив эту систему, получим, что х = 300; у = 200. Значит, один мешочек содержит 300 грамм малахита, а граната – 200 грамм. Ответ: 300 грамм самоцветов содержится в каждом мешочке с малахитом и 200 грамм в каждом мешочке с гранатом.
Выбранный для просмотра документ Решение задач, сводящихся к системам линейных уравнений.doc
Фрагменты уроков по теме: «Решение задач, сводящихся к системам линейных уравнений»
Фрагмент урока № 1.
Тема: Решение текстовых задач с помощью систем линейных уравнений.
Цель: Познакомить учащихся с алгоритмом решения текстовых задач, сводящихся к системам линейных уравнений.
Сформировать у учащихся умение применять системы линейных уравнений при решении задач;
Развивать память по средствам воспроизведения пройденных ранее определений и понятий, грамотную математическую речь, способствовать повышению уровня познавательной деятельности;
Воспитывать аккуратность в ходе ведения записей в тетради, внимательность.
Тип урока: Изучение нового материала.
I. Организационный момент.
II. Актуализация знаний.
Приемы: Фронтальный опрос
Повторить определение линейного уравнения, системы линейных уравнений, способы их решения. Вспомнить, что называется текстовой задачей, методы и этапы ее решения. Решение линейных уравнений и их систем.
III Изучение нового материала.
Методы: словесный, наглядный
Приемы: эвристическая беседа, демонстрация (см. Презентация)
Этап изучения нового материала предусматривает использование эвристической беседы, как способа активизации познавательной деятельности учащихся.
Сумма двух чисел равна 63, а их разность равна 12. Найдите эти числа.
— Внимательно читаем задачу. Что нужно найти в задаче? (Два числа)
— Можем ли сразу найти эти числа? (Нет)
— Почему? (Потому что ни одно из них неизвестно)
— Что нам известно об этих числах? (Их сумма равна 63, а разность 12)
— Вспомните, что мы повторяли в начале урока. Каким же методом будем решать эту задачу? (Алгебраическим, составим уравнение)
— Сколько же уравнений получится? (Два)
— Действительно и полученные уравнения мы запишем системой.
Решение. Пусть х первое число, а у — второе. По условию задачи сумма двух чисел равна 63, поэтому
Известно, что разность этих чисел равна 12. Значит 
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
— Каким методом рациональнее решать данную систему уравнений? (Методом алгебраического сложения)
— Значение х подставим в первое уравнение
-Решив эту систему, получим, что
— Каким способом будем выполнять проверку задачи? (Решение обратной задачи)
Проверка. Составим обратную задачу. Известны два числа 25,5 и 37, 5, необходимо найти их сумму и разность.
1) 37,5+25,5 = 63 – сумма двух чисел;
2) 37,5 – 25,5 = 12 – разность чисел.
— Какой можем сделать вывод после выполнения проверки? (Задача решена верно)
Ответ: первое число равно 37,5; второе число равно 25,5.
— Сформулируем алгоритм решения задач, сводящихся к системам линейных уравнений.
Рекомендуем к изучению алгоритма решения задач, сводящихся к системам линейных уравнений применить неимитационный метод активизации познавательной деятельности, прием: самостоятельная работа с литературой.
При решении задач с помощью систем уравнений поступают следующим образом:
Обозначают некоторые неизвестные числа буквами и, используя условия задачи, составляют систему уравнений;
Решают эту систему;
Истолковывают результат в соответствии с условием задачи.
IV. Закрепление изученного материала.
Приемы: письменные упражнения
— Используем полученный алгоритм при решении следующей задачи.
Один ученик выполняет решение у доски, остальные в тетрадях (записи должны быть развернутыми и сопровождаться соответствующими устными рассуждениями).
Техническое перевооружение цеха позволило выпустить в феврале на 165 изделий больше, чем в январе. Сколько изделий было выпущено в январе и сколько в феврале, если известно, что за эти месяцы цех выпустил 1315 изделий?
Решение. Для решения задачи выполним все этапы сформулированного ранее алгоритма.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений.
Пусть х изделий было выпущено в феврале, а у изделий — в январе. Зная, что в феврале было выпущено на 165 изделий больше, чем в январе составим уравнение
По условию задачи за эти месяцы цех выпустил 1315 изделий, значит
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему.
Решим эту систему методом алгебраического сложения.
Значение х подставим в первое уравнение
3) Истолковываем результат в соответствии с условием задачи.
Решив эту систему, получим, что х =740; у =575. Значит, 575 изделий было выпущено в январе, а в феврале было выпущено 740 изделий.
Проверка. Составим обратную задачу. В январе было выпущено 575 изделий. Техническое перевооружение цеха позволило выпустить в феврале 740 изделий. На сколько больше изделий было выпущено в феврале, чем в январе и сколько изделий выпустил цех за эти два месяца?
1) 740 — 575=165 (изделий);
2) 740+575=1315(изделий) – выпустил цех за эти два месяца.
— Какой можем сделать вывод после выполнения проверки? (Задача решена верно)
Ответ: 575 изделий было выпущено в январе, а в феврале было выпущено 740 изделий.
V. Домашнее задание. Задание, направленное на формирование умения работать по алгоритму к задачам и умения вычленять условия и требования.
Фрагмент урока № 2.
Тема: Решение текстовых задач с помощью систем линейных уравнений.
Цель: Закрепить знания и умения учащихся решать задачи с помощью систем линейных уравнений.
Формировать у учащихся умение решать задачи с помощью систем линейных уравнений;
Развивать память по средствам воспроизведения пройденных ранее определений и понятий, грамотную математическую речь, способствовать повышению уровня познавательной деятельности;
Воспитывать аккуратность в ходе выполнения записей в тетрадях, самостоятельность, внимательность.
Тип урока: Закрепление знаний и умений.
I. Организационный момент.
II. Актуализация знаний.
Приемы: фронтальный опрос
Повторить определение линейного уравнения, системы линейных уравнений, способы их решения. Вспомнить, что называется текстовой задачей, методы и этапы ее решения. Алгоритм решения текстовых задач, сводящихся к решению системы линейных уравнений.
III. Закрепление изученного материала.
Приемы: письменные упражнения, самостоятельная работа.
При решении задачи мы использовали прием активизации познавательной деятельности учащихся – самостоятельная работа.
В Зоопарке живет много разных животных. Среди них есть лисы – черные и рыжие. Известно, что всего в зоопарке живет 7 лис, а черных на 3 лисы меньше, чем рыжих. Сколько черных и рыжих лис живет в зоопарке?
Решение. Для решения задачи выполним все этапы сформулированного ранее алгоритма.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений.
Пусть в зоопарке живет х черных лисиц и у рыжих. Зная, всего в зоопарке живет 7 лисиц, составим уравнение х + у = 7.
По условию задачи черных лисиц на 3 меньше, чем рыжих, значит у – х = 3.
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему.
Решим эту систему методом алгебраического сложения.
Значение у подставим во второе уравнение
3) Истолковываем результат в соответствии с условием задачи.
Решив эту систему, получим, что
Проверка. Составим обратную задачу. В Зоопарке живет много разных животных. Среди них есть лисы – черные и рыжие. Черных лисиц в зоопарке живет 2, а рыжих — 5. Сколько всего лис живет в зоопарке? На сколько больше рыжих лис живет в зоопарке, чем черных?
1) 5+2=7 (лис) – черных и рыжих вместе;
Ответ: В зоопарке 5 рыжих лисиц и 2 черные лисицы.
Рекомендуется использовать взаимоконтроль для проверки .
Для решения данной задачи используется наглядный метод – демонстрация (см. Презентация).
Один ученик выполняет решение задачи у доски, остальные в тетрадях (записи должны быть развернутыми и сопровождаться соответствующими устными рассуждениями).
Старик Кокованя приютил у себя сироту. Девочка Даренка была смышленая и чудная. Встретилась она с волшебным козлом, которого прозвали Серебряное копытце. При каждой встрече с ним можно было собрать много каменьев. При первой встрече Даренка собрала два мешочка гранатов и три мешочка малахита, всего 1300 гр. А при второй встрече один мешочек гранатов и два мешочка малахит, всего 800 грамм. Сколько грамм самоцветов содержится в каждом мешочке с малахитом и в каждом мешочке с гранатом?
Решение. Для решения задачи выполним все этапы сформулированного ранее алгоритма.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений.
Пусть х грамм содержит один мешочек малахитов, а у грамм — самоцветов. Зная, что при первой встрече Даренька собрала два мешочка гранитов и три мешочка малахита, составим уравнение
По условию задачи при второй встрече Даренька собрала один мешочек гранатов и два мешочка малахит, всего 800 грамм, значит
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему.
Решим эту систему методом подстановки. Выразим переменную у из второго уравнения и подставим в первое.
Значение х подставим во второе уравнение
3) Истолковываем результат в соответствии с условием задачи.
Решив эту систему, получим, что 
Ответ: 300 грамм самоцветов содержится в каждом мешочке с малахитом и 200 грамм в каждом мешочке с гранатом.
IV. Домашнее задание. Задание, направленное на формирование умения работать по алгоритму к задачам и умения вычленять условия и требования.
Фрагмент урока № 3 .
Тема: Решение текстовых задач с помощью систем линейных уравнений.
Цель: Углубить знания учащихся о методах решения текстовых задач.
Закреплять умение решать текстовые задачи с помощью систем линейных уравнений. Использовать полученные знания при работе с математическими моделями реальных ситуаций;
Развивать память по средствам воспроизведения пройденных ранее определений и понятий, грамотную математическую речь, способствовать повышению уровня познавательной деятельности;
Воспитывать интерес к изучению математики, аккуратность в ходе выполнения записей в тетрадях, самостоятельность, внимательность.
Тип урока: Закрепление знаний и умений.
I. Организационный момент.
II. Актуализация знаний.
Приемы: фронтальный опрос
Повторить определение линейного уравнения, системы линейных уравнений, способы их решения. Вспомнить, что называется текстовой задачей, методы и этапы ее решения. Вспомнить формулы нахождения пути, скорости, времени. Перевод одной единицы измерения в другую.
III. Закрепление материала.
Методы: практический (имитационный)
Приемы: письменные упражнения, коллективная мыслительная деятельность .
При решении задачи рекомендуется использовать имитационный метод активизации познавательной деятельности, прием — коллективная мыслительная деятельность , то есть учащиеся самостоятельно решают задачу, консультируясь с товарищами.
За 4 ч езды на автомашине и 7 ч езды на поезде туристы проехали 640 км. Какова скорость поезда, если она на 5 км/ч больше скорости автомашины?
Решение. Воспользуемся алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений.
Пусть х км/ч скорость автомашины, а у км/ч скорость поезда.
Известно, что скорость поезда на 5 км/ч больше скорости автомашины. Значит
Зная, что за 4 ч езды на автомашине и 7 ч езды на поезде туристы проехали 640 км составим уравнение
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему.
Решим систему методом подстановки. Выразим переменную у из первого уравнения и подставим во второе.
Решив эту систему, получим, что х =55; у =60.
3) Истолковываем результат в соответствии с условием задачи.
Скорость поезда 60 км/ч, а скорость автомашины 55 км/ч.
Проверка. Составим обратную задачу. Скорость поезда 60 км/ч, а скорость автомашины 55 км/ч. Сколько туристы проедут километров за 4 ч езды на автомашине и 7 ч езды на поезде?
1) 60·7=420 (км) – проедут туристы на поезде;
2) 55·4=220 (км) – проедут туристы на автомашине;
3) 220+420=640 (км) — проедут туристы на поезде и на автомашине вместе.
Ответ: 60 км/ч скорость поезда.
При решении задачи рекомендуется использовать самостоятельную работу, как прием активизации познавательной деятельности.
Из пунктов А и В, расстояние между которыми равно 280 км, выходят одновременно два автомобиля. Если автомобили будут двигаться навстречу друг другу, то встреча произойдет через 2 ч. Если же они будут двигаться в одном направлении то автомобиль, вышедший из А, догонит автомобиль вышедший из В, через 14 ч. Какова скорость каждого автомобиля?
Решение. Воспользуемся алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений:
Пусть х км/ч скорость первого автомобиля, а у км/ч скорость второго автомобиля.
Зная, что через 2 часа движения навстречу друг другу автомобили встретятся, а расстояние между пунктом А и пунктом В равно 280, составим уравнение 
Известно, что если автомобили будут двигаться в одном направлении, то автомобиль, вышедший из А, догонит автомобиль вышедший из В, через 14 ч. Составим уравнение 
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему:
Решим систему методом алгебраического сложения.
Подставим значение х в первое уравнение системы.
Решив эту систему, получим, что х =80; у =60.
3) Истолковываем результат в соответствии с условием задачи.
Скорость первого автомобиля равна 80 км/ч, а скорость второго автомобиля 60 км/ч.
Ответ: 80 км/ч скорость первого автомобиля, 60 км/ч скорость второго автомобиля.
Рекомендуется использовать взаимоконтроль для проверки .
IV. Домашнее задание.
Фрагмент урока № 4.
Тема: Системы линейных уравнений и их решения.
Цель: Обобщить и систематизировать знания учащихся по теме «Системы линейных уравнений и их решения».
Совершенствовать у учащихся навык решения систем линейных уравнений и текстовых задач, сводящихся к системам линейных уравнений;
Развивать память по средствам воспроизведения пройденных ранее определений и понятий, грамотную математическую речь, способствовать повышению уровня познавательной деятельности;
Воспитывать интерес к изучению математики, умение работать в коллективе, внимательность.
Тип урока: Обобщение и систематизация знаний, умений, навыков.
Форма организации: дидактическая игра.
I. Организационный момент.
Учитель делит детей на 4 команды равной силы.
II. Основная часть.
Методы: словесные, практические (имитационные)
Приемы: письменные и устные упражнения, фронтальный опрос, фронтальная работа, коллективная письменная деятельность.
Этап предусматривает использование дидактической игры, для активизации познавательной деятельности учащихся .
За каждое правильно выполненное задание команда получает 1 балл. За нарушение дисциплины команда получает 1 штрафной балл.
1. Разминка . Учащиеся решают линейные уравнения.
2. Конкурс капитанов . Капитаны решают по одной линейной системе уравнений.
3. Теоретический . Команды отвечают на вопросы. 1 вопрос каждому участнику.
Определение линейного уравнения, системы линейных уравнений, способы их решения. Определение текстовой задачей, методы и этапы ее решения и тп.
4. Заключительный . Учитель дает 2 задачи каждой команде и задает вопросы всем участникам.
На строительстве объекта работает 31 бригада. В их числе бригад, работающих на бригадном подряде, на 5 больше, чем других. Сколько бригад работает на бригадном подряде?
Решение. Воспользуемся алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений:
Пусть на бригадном подряде работают х бригад, а у бригад работают на других объектах. Зная, что всего на строительстве работает 31 бригада, составим уравнение
Известно, что число бригад, работающих на бригадном подряде, на 5 больше, чем других. Значит
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему:
Решим систему методом алгебраического сложения.
Значение х подставим во второе уравнение
Решив эту систему, получим, что х =18; у =13.
3) Истолковываем результат в соответствии с условием задачи
18 бригад работают на бригадном подряде, а остальных 13 бригад.
Ответ: На бригадном подряде работают 18 бригад.
В мастерских отремонтировали 22 легковых и грузовых автомобиля. Среди них легковых было на 8 меньше, чем грузовых. Сколько грузовых автомобилей отремонтировали в мастерских?
Решение. Воспользуемся алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.
1) Обозначим некоторые неизвестные числа буквами и, используя условия задачи, составим систему уравнений:
Пусть отремонтировали в мастерских х грузовых автомобилей и у легковых автомобилей. Зная, что всего отремонтировали 22 автомобиля, составим уравнение
Известно, что отремонтировали легковых автомобилей на 8 меньше, чем грузовых. Значит
Чтобы ответить на вопрос задачи, надо найти такие значения х и у , которые удовлетворяют как первому, так и второму уравнению, то есть удовлетворяют системе
2) Решим эту систему:
Решим систему методом алгебраического сложения.
Значение х подставим в первое уравнение.
Решив эту систему, получим, что х =15; у =7.
3) Истолковываем результат в соответствии с условием задачи:
В мастерских отремонтировали 15 грузовых и 7 легковых автомобилей.
Ответ: 15 грузовых автомобилей отремонтировали в мастерских.
Вопросы к задачам.
Как вы решали задачу № 1? (Воспользовались алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.)
Как вы решали задачу № 2? (Воспользовались алгоритмом решения текстовых задач, сводящихся к линейным системам уравнений.)
Сформулируйте алгоритм решения текстовых задач, сводящихся к линейным системам уравнений.
Какой методом применили при решении линейной системы уравнений в задаче № 1? (Методом алгебраического сложения.)
Почему вы воспользовались этим методом решения линейных систем уравнений? (Этот метод является более рациональным для данной системы.)
Какой методом применили при решении линейной системы уравнений в задаче № 2? (Методом алгебраического сложения.)
IV. Итог урока. Подведение итогов. Награждение.
http://reshator.com/sprav/algebra/7-klass/resheniya-zadachi-s-pomoshchyu-sistemy-linejnyh-uravnenij/
http://infourok.ru/fragmenti-urokov-po-matematike-reshenie-zadach-svodyaschihsya-k-sistemam-lineynih-uravneniy-1279075.html