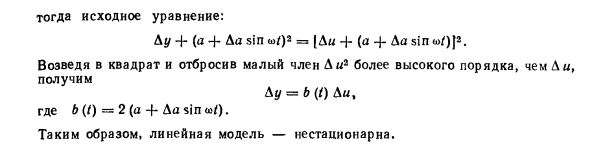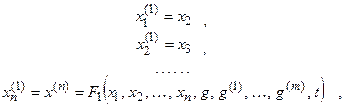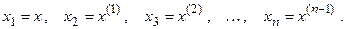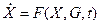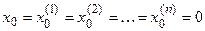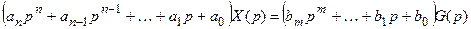Уравнения динамики и статики. Линеаризация






Уравнения динамики и статики. Линеаризация
- Динамические и статические уравнения. Линеаризация В общем случае звенья и системы описываются нелинейными дифференциальными уравнениями произвольного порядка. Ссылка — это математическая модель элемента. Например, рассмотрим ссылку (рисунок 2.1). Связь может быть описана квадратным дифференциальным уравнением f [y, y, y, u, u) + f = 0, (2.1) Где у — выходная величина, f — входная величина, £ / и Первая производная, у — вторая производная. Уравнение (2.1), которое описывает процесс в звене при любом входном действии, называется динамическим уравнением.
Остановитесь на определенной входной величине u = и / = Pns. 2.1. Процесс по ссылке устанавливается со временем xa: выходное значение принимает постоянное значение y = y0. (2.1) принимает следующий вид U UD 0, 0 и \ 0) + / ° = 0. (2.2) Это уравнение представляет статическое или стационарное состояние и называется статическим уравнением. Статический режим может быть описан графически с использованием статических свойств.
Статическая характеристика ссылки или элемента (и системы) — это зависимость выходного значения от входного значения в статическом режиме. Людмила Фирмаль
Статические характеристики можно построить экспериментально, применяя постоянный эффект к входу элемента и измеряя выходное значение после завершения процесса перехода, или путем расчета с использованием статического уравнения. Если ссылка имеет несколько входов, она описывается с использованием семейства статических характеристик. Например, ссылка, характеризуемая уравнением статического режима (2.2), может быть графически описана с использованием семейства статических свойств. Статическая характеристика представляет собой кривую зависимости выходной величины y от одной входной величины и / или — / (или u) от различных других фиксированных значений.
Линеаризация. Автоматические системы обычно описываются нелинейными дифференциальными уравнениями. Однако во многих случаях они могут быть линеаризованы. Замените исходные нелинейные уравнения линейными уравнениями, которые приблизительно описывают процессы в системе. Процесс преобразования нелинейного уравнения в линейный называется линеаризацией. Автоматизированная система должна поддерживать некоторые режимы конфигурации. В этом режиме входные и выходные значения системной ссылки изменяются в соответствии с определенными правилами.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В частности, система стабилизации принимает определенное постоянное значение. Однако, поскольку фактический режим отличается от требуемого (заданного) режима из-за различных возмущающих факторов, текущие значения входных и выходных величин не равны значениям, соответствующим указанному режиму. В функционирующей системе аутизма фактический режим немного отличается от требуемого режима, и отклонение входных и выходных значений строительного блока от требуемых значений является небольшим. Это позволяет линеаризовать путем разложения нелинейной функции уравнения в ряд Тейлора.
Пример 2.1. Выше поясняется на примере ссылки, описанной в уравнении (2.1). Соответствовать указанному режиму и = и *, и = и *; / = / ! / = (/ ‘, Y = Y *, y ** y *. (2.3) Указывает отклонение фактических значений u, / и y от значений, требуемых для Dm, D / и Lu, т. Е. A и -u-u *, Af = f- / *, Ay = y-y *. Тогда u = u * 4-Aw, u = m * + Au, f = f * + D /, y = y * + Au, Y-y * + A
Линеаризация может быть выполнена по ссылкам. Людмила Фирмаль
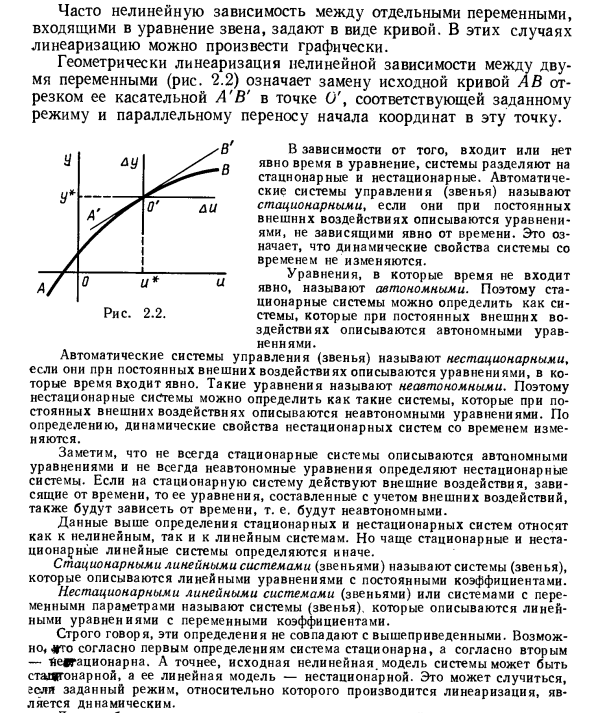
Уравнение (2.5) было получено при следующих допущениях: Функция F имеет непрерывные частные производные по всем аргументам вблизи точки, соответствующей данной моде. Если хотя бы одно из этих условий не выполняется, линеаризация не может быть выполнена. Для первого условия вы должны знать следующее: Невозможно уменьшить все отклонения одновременно. Это зависит от типа нелинейности. Во многих случаях нелинейные отношения между отдельными переменными в уравнении связи задаются в форме кривой. В этих случаях линеаризация может быть выполнена графически.
Геометрическая линеаризация нелинейной зависимости между двумя переменными (рис. 2.2) должна заменить исходную кривую A этого касательного сегмента A’B, соответствующего конкретной моде, и этой точке Это означает перевод происхождения. Рисунок 2.2. В зависимости от того, явно ли время входит в уравнение, система делится на стационарную и нестационарную. Автоматическая система управления (ссылка) называется стационарной, когда она описывается явным не зависящим от времени уравнением при определенных внешних воздействиях.
Это означает, что динамические свойства системы не меняются со временем. Уравнение, которое явно не включает время, называется автономией. Таким образом, стационарная система может быть определена как система, описываемая автономными уравнениями при определенных внешних воздействиях. Автоматическая система управления (ссылка) называется неустановившейся, если она описывается уравнением, в которое время вводится явно при определенных внешних воздействиях. Такое уравнение называется неавтономным. Таким образом, нестационарная система может быть определена как система, описываемая неавтономным уравнением при определенных внешних воздействиях.
По определению динамические характеристики нестационарных систем меняются со временем. Обратите внимание, что стационарные системы не всегда описываются автономными уравнениями, а неавтономные уравнения не всегда определяют нестационарные системы. Если зависящие от времени внешние эффекты действуют на стационарную систему, уравнения, составленные для внешних воздействий, также зависят от времени. То есть они не автономны. Приведенные выше определения стационарных и нестационарных систем относятся как к нелинейным, так и к линейным системам. Однако чаще определение фиксированных и нефиксированных линейных систем различается. Стационарная линейная система (звено) называется системой (звено) и описывается линейным уравнением с постоянными коэффициентами.
Переходные линейные системы (звенья) или системы с переменными параметрами называются системами (звеньями) и описываются линейными уравнениями с переменными коэффициентами. Строго говоря, эти определения не соответствуют вышеприведенному. Возможно, согласно первому определению, 4го является стационарной системой, а согласно второму определению яйцо является стационарным. Точнее, исходная нелинейная модель системы статзонарна, а ее линейная модель нестационарна. Это может произойти, и режим спецификации геля, связанный с выполнением линеаризации, является динамическим. Кроме того, следует второе определение. Первый может быть связан только с нелинейными системами.
Пример 2.2 Напишите статическую нелинейную статическую связь с уравнением y = / A. Линеаризовать относительно данного режима И * = a 4-да, грех y * = (a-J-да, грех W) 2. Об отклонении Lj / = y / -y * -y- (a H-yes sin w /) 2, Di-u-u * = u- (a-f-Yes sin w /), Исходное уравнение: & Y + (a-f sin®> /) 2 = [yes-f (a-fyessin (OD «, Где b (/) = 2 (a-f yes sinoo /). Таким образом, линейная модель является переходной.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнения динамики и статики
При проектировании и исследовании САУ необходимо знать уравнения, описывающие их движения. Процессы в САУ описываются дифференциальными, разностными, интегральными и интегро-дифференциальными уравнениями, которые называют ее математической моделью. При исследовании САУ на различных этапах математическая модель может быть различной. Начинают исследования САУ с простейшей математической моделью, а затем ее усложняют, учитывая дополнительные связи и влияния. Такой подход объясняется тем, что к математической модели предъявляются противоречивые требования. Математическая модель должна достаточно полно описывать динамику САУ и при этом быть по возможности простой.
В дальнейшем будут рассматриваться только обыкновенные дифференциальные уравнения, в неявной форме которые могут быть записаны
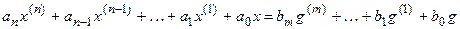
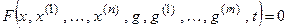
| x, x ( i ) | — управляемая (выходная) величина и ее производные 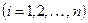 ; ; |
| g, g ( j ) | — задающая (входная) величина и ее производные 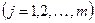 ; ; |
| ai и bj | — постоянные коэффициенты, зависящие от параметров системы; |
| с и m | — числа, определяющие порядок производных 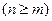 , причем n определяет порядок дифференциального уравнения; , причем n определяет порядок дифференциального уравнения; |
| t | — независимая переменная (время). |
Уравнения (3.1) и (3.2) могут быть записаны в явной форме, разрешенные относительно старшей производной (например, (3.2))
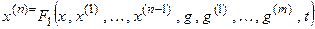
Данное дифференциальное уравнение в явной форме n-го порядка можно преобразовать в систему n дифференциальных уравнений первого порядка:
путем введения новых неизвестных
Если в дифференциальное уравнение (3.2) входит n неизвестных функций 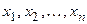
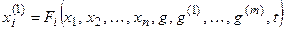
где 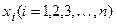
В векторной форме дифференциальное уравнение будет иметь вид


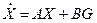
| где | X – вектор выходных величин (параметров состояний); |
| G – вектор задающих (входных) величин; | |
| A – матрица объекта управления с элементами aij; | |
| B – матрица задающих величин с элементами bij . |
Широкое применение в ТАУ получила операторная форма записи дифференциального уравнения. Это объясняется тем, что от дифференциального уравнения посредством интегрального преобразования (например, преобразования Лапласа) переходят к операторной форме. Операторное уравнение является алгебраическим и его решение проще, чем дифференциальное. Затем из полученного решения операторного уравнения с помощью обратного преобразования получают решение дифференциального уравнения.
Дифференциальное уравнение (3.1) при нулевых начальных условиях
в операторной форме можно записать
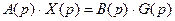
где 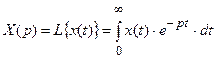
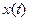
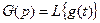
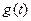
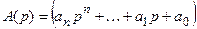
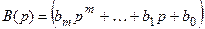
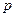
Операторная форма записи дифференциального уравнения, когда начальные условия по всем переменным равны нулю, совпадает с символической формой, когда 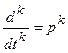
Уравнение движения САУ в любой форме полностью описывает весь процесс управления, т.е. процесс изменения управляемых величин как в переходном, так и в установившемся режимах.
Под установившимся режимом понимают процесс, при котором регулируемая (управляемая) величина изменяется по закону, определяемому лишь законом изменения задающего воздействия. Установившейся режим САУ, относительно которого рассматривается движение системы в процессе управления, называется исходным.
Переходным режимом называется изменение управляемой величины при переходе САУ из одного в другое установившееся состояние.
Если в установившемся режиме воздействия после их приложения больше не изменяют своих величин во времени, то в САУ устанавливается так называемый статический режим.
Уравнение статики может быть получено из уравнения движения САУ (3.1), если все члены, содержащие производные, приравнять нулю, то есть
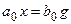
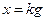
где 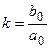
Графическое отображение данной зависимости, т.е. зависимости между выходной x и входной g величинами САУ в статическом режиме, называется статической характеристикой (рис. 3.1).
 |
Рис.3.1. Статические характеристики элементов САУ
Статические характеристики элементов САУ и систем в целом могут быть как линейными (кривая 1, рис. 3.1), так и нелинейными (кривая 2, рис. 3.1). Если характеристика нелинейная, то необходимо учитывать влияние данной нелинейности на динамику САУ.
Дата добавления: 2015-12-11 ; просмотров: 1345 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Общее уравнение динамики. Пример решения задачи
Условие задачи
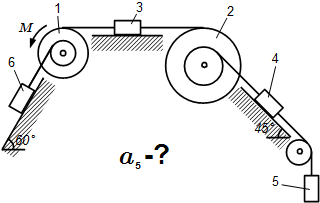
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R 1 = 0,2 м , r 1 = 0,1 м , а шкива 2 – R 2 = 0,3 м , r 2 = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ 1 = 0,1 м и ρ 2 = 0,2 м .
Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.
Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).
Решение задачи
Дано: R 1 = 0,2 м , r 1 = 0,1 м , R 2 = 0,3 м , r 2 = 0,15 м , ρ 1 = 0,1 м , ρ 2 = 0,2 м . P 1 = 40 Н , P 2 = 0 , P 3 = 0 , P 4 = 20 Н , P 5 = 30 Н , P 6 = 10 Н , M = 10 Н·м .
Установление кинематических соотношений
Установим кинематические соотношения. Пусть V 4 , V 5 , V 6 , a 4 , a 5 , a 6 , δS 4 , δS 5 , δS 6 – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω 1 , ω 2 , ε 1 , ε 2 , δφ 1 , δφ 2 – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.
Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.
Итак, мы нашли связь между скоростями тел.
;
;
.
Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.
Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.
Активные внешние силы
Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P 1 = 40 Н , P 4 = 20 Н , P 5 = 30 Н и P 6 = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N 1 , N 2 и N шкивов 1, 2 и невесомого блока;
силы реакции N 4 и N 6 , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.
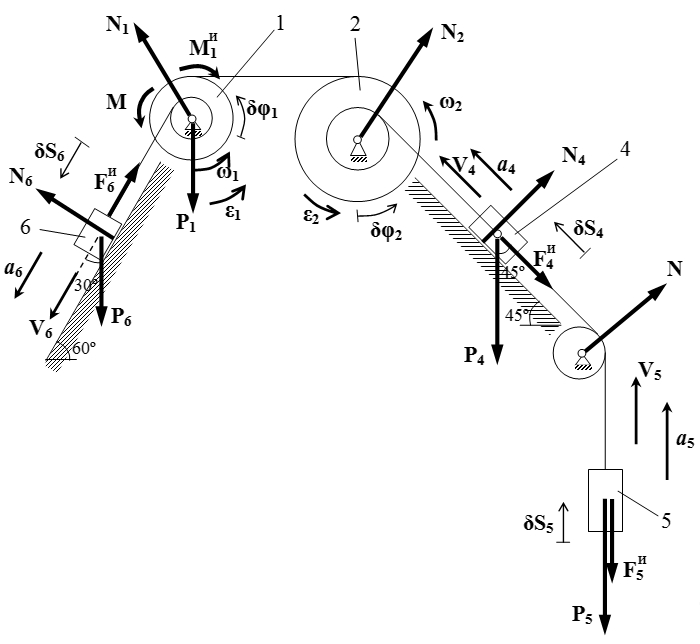
Силы инерции
Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.
Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε 1 и ε 2 , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a 4 , a 5 и a 6 , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a 5 . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).
Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a 5 .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.
Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.
Применение общего уравнения динамики
Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS 5 . Тогда угол поворота δφ 1 шкива 1 и перемещения δS 4 и δS 6 грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.
Определение суммы работ внешних активных сил и сил инерции
Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.
Работа, произведенная моментом сил , вычисляется аналогично:
.
Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P 1 , N 1 , N 2 и N не совершают работу. Поскольку силы N 4 и N 6 перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.
Находим сумму работ остальных активных сил и сил инерции.
.
Подставляем выражения для сил инерции и применяем кинематические соотношения.
.
Сокращаем на δS 5 и преобразовываем.
.
Подставляем численные значения.
;
;
м/с 2 .
Автор: Олег Одинцов . Опубликовано: 02-08-2015
http://helpiks.org/6-18020.html
http://1cov-edu.ru/mehanika/dinamika-tel/obschee-uravnenie-dinamiki-primer-resheniya-zadachi/