Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
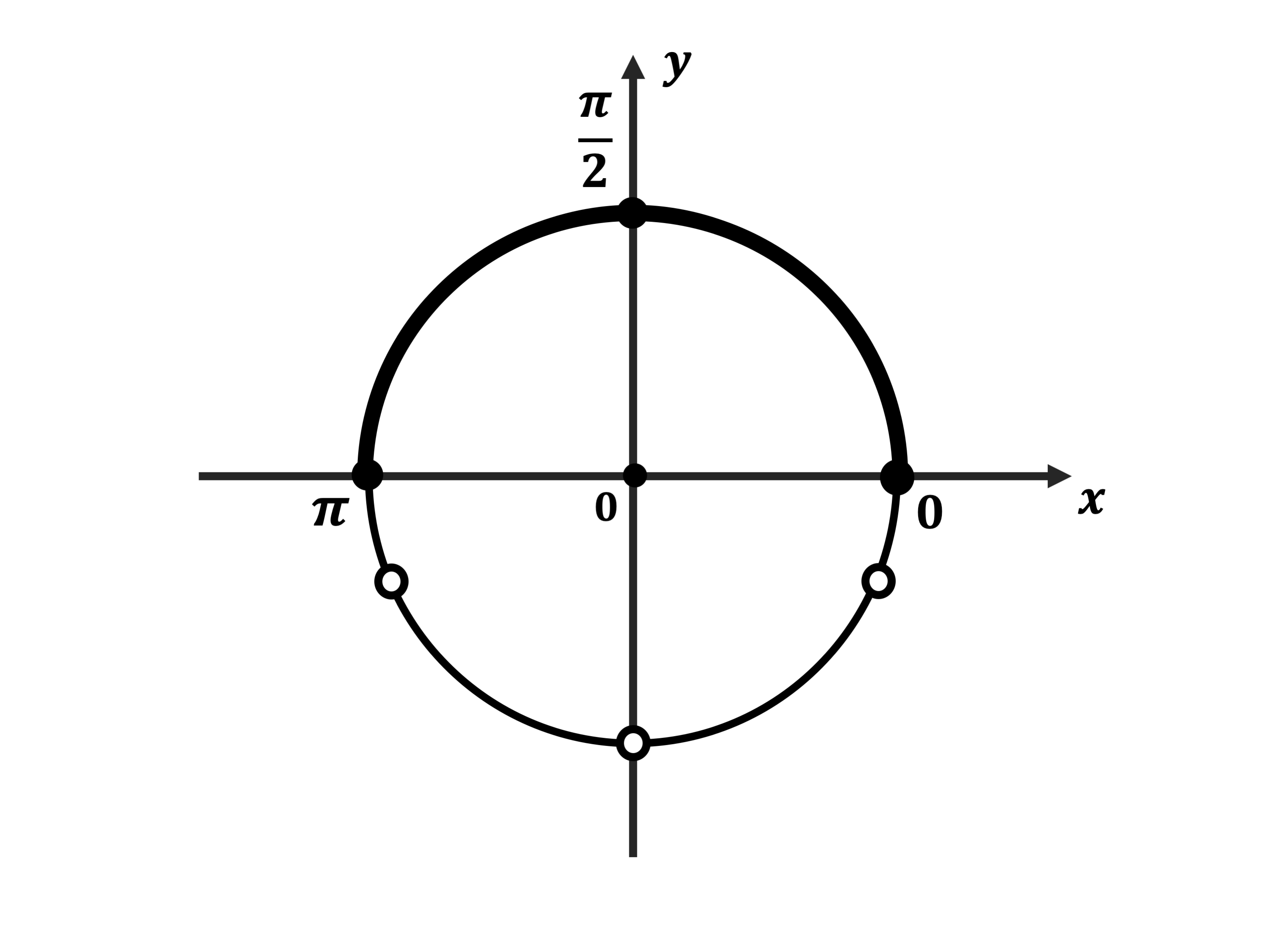
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
Задание 12. Уравнения. ЕГЭ 2022 по математике профильного уровня
Задачи для практики
Задача 1
а) Решите уравнение $11\cos 2x=7\sin (x- <π>/ <2>)-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
$11(2\cos^2 x-1)=-7\cos x-9$,
$22\cos^2 x -11+7\cos x +9=0$,
$22\cos^2 x+7\cos x -2=0$.
Обозначим $\cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + <π>/<2>)- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-<π>/<2>]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$t_1 = <−7 − 9>/ <2·2>= −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
Вернёмся к исходной переменной:
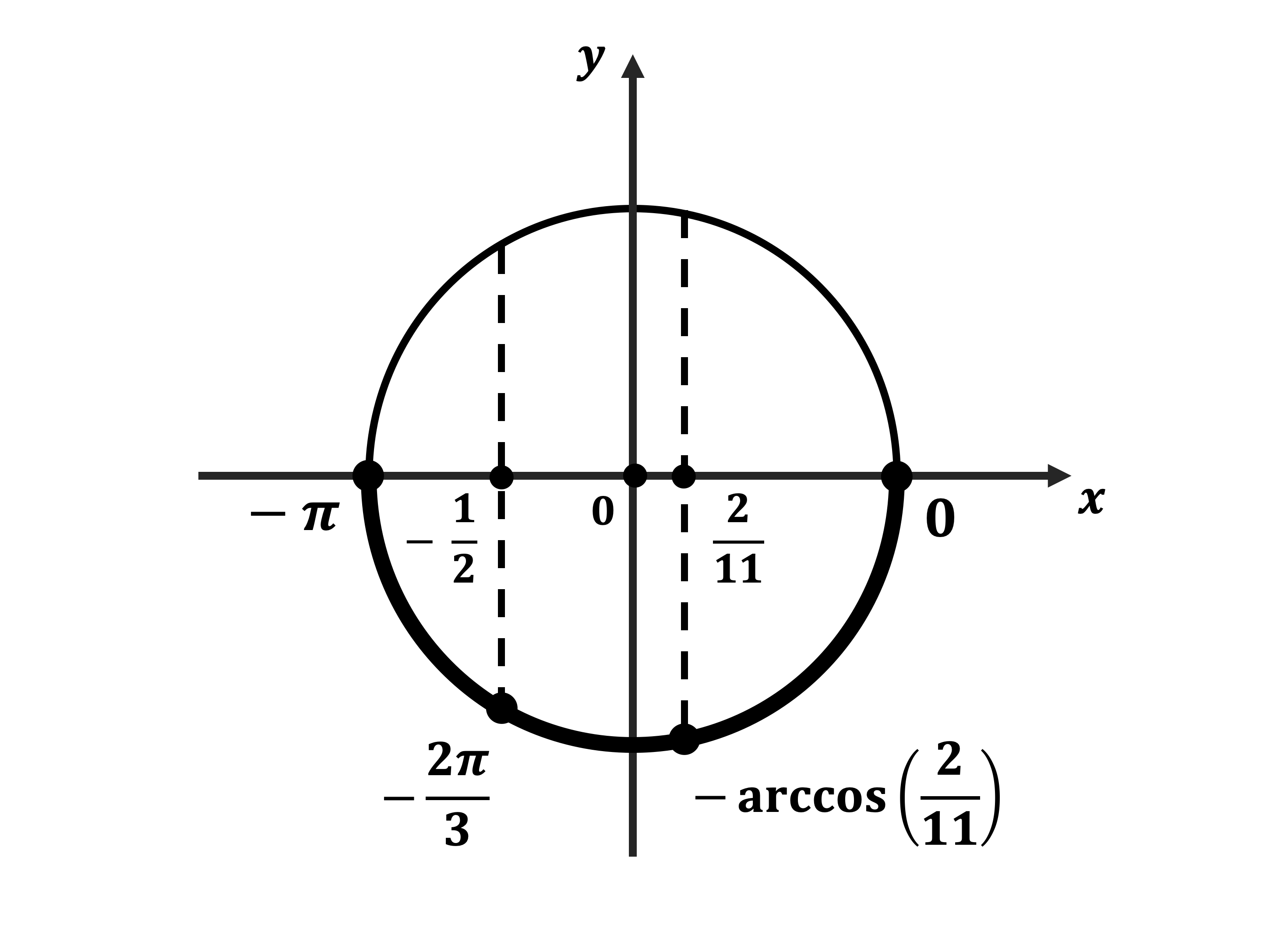
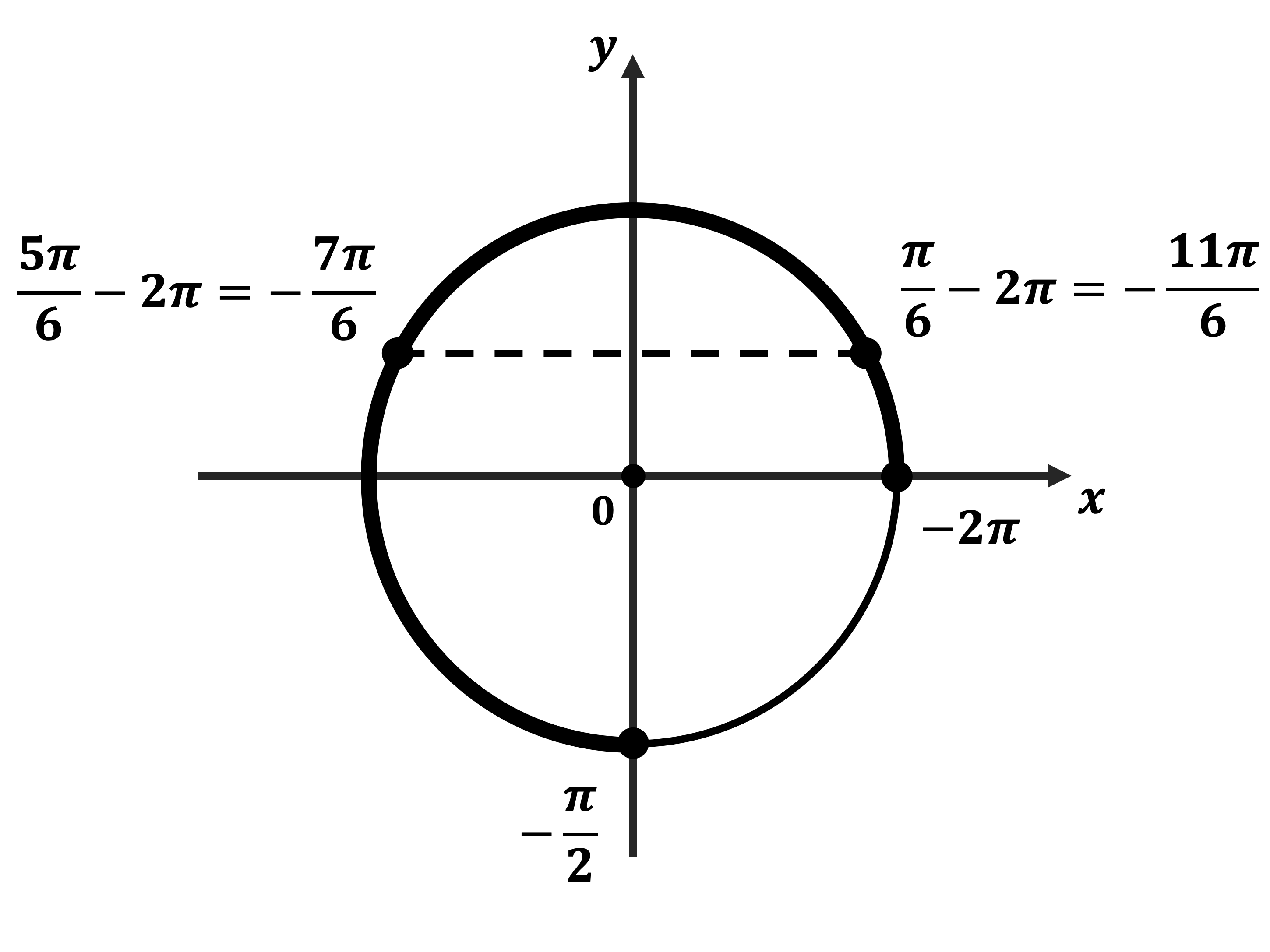
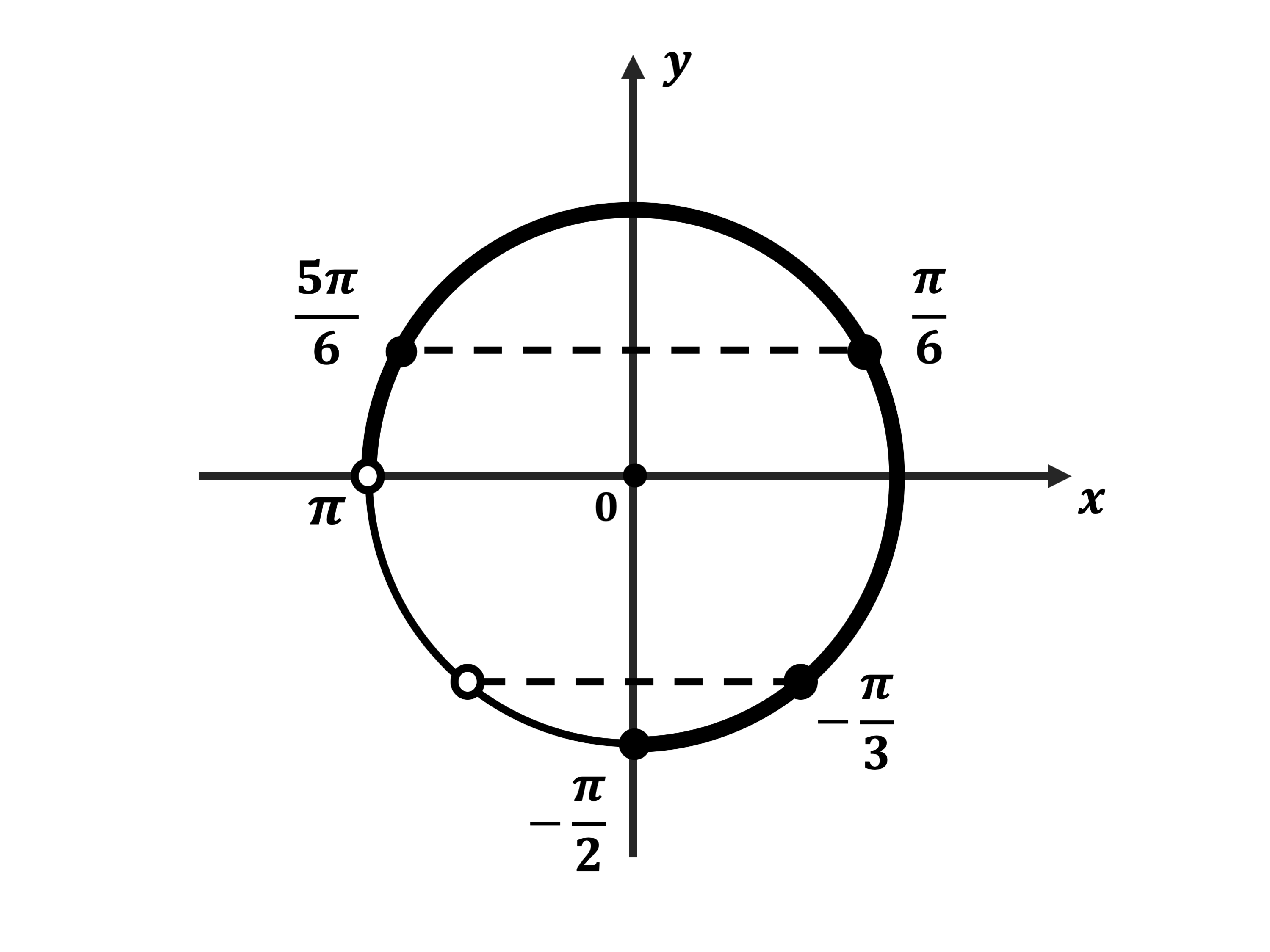
б) Корни, принадлежащие отрезку $[-2π; —<π>/<2>]$, найдём с помощью единичной окружности. Получим: $<π>/<6>-2π=-<11π>/<6>; <5π>/<6>-2π=-<7π>/<6>$.
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + <3π>/<2>)+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[<π>/<2>;<3π>/<2>]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = <−5 − 3>/ <2·2>= −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = <−5 + 3>/ <2· 2>= −<1>/<2>$.
Вернёмся к исходной переменной: $cos x = − <1>/<2>$,
$x = ±(π − <π>/<3>) + 2πn, n ∈ Z , x = ±<2π>/ <3>+ 2πn, n ∈ Z.$
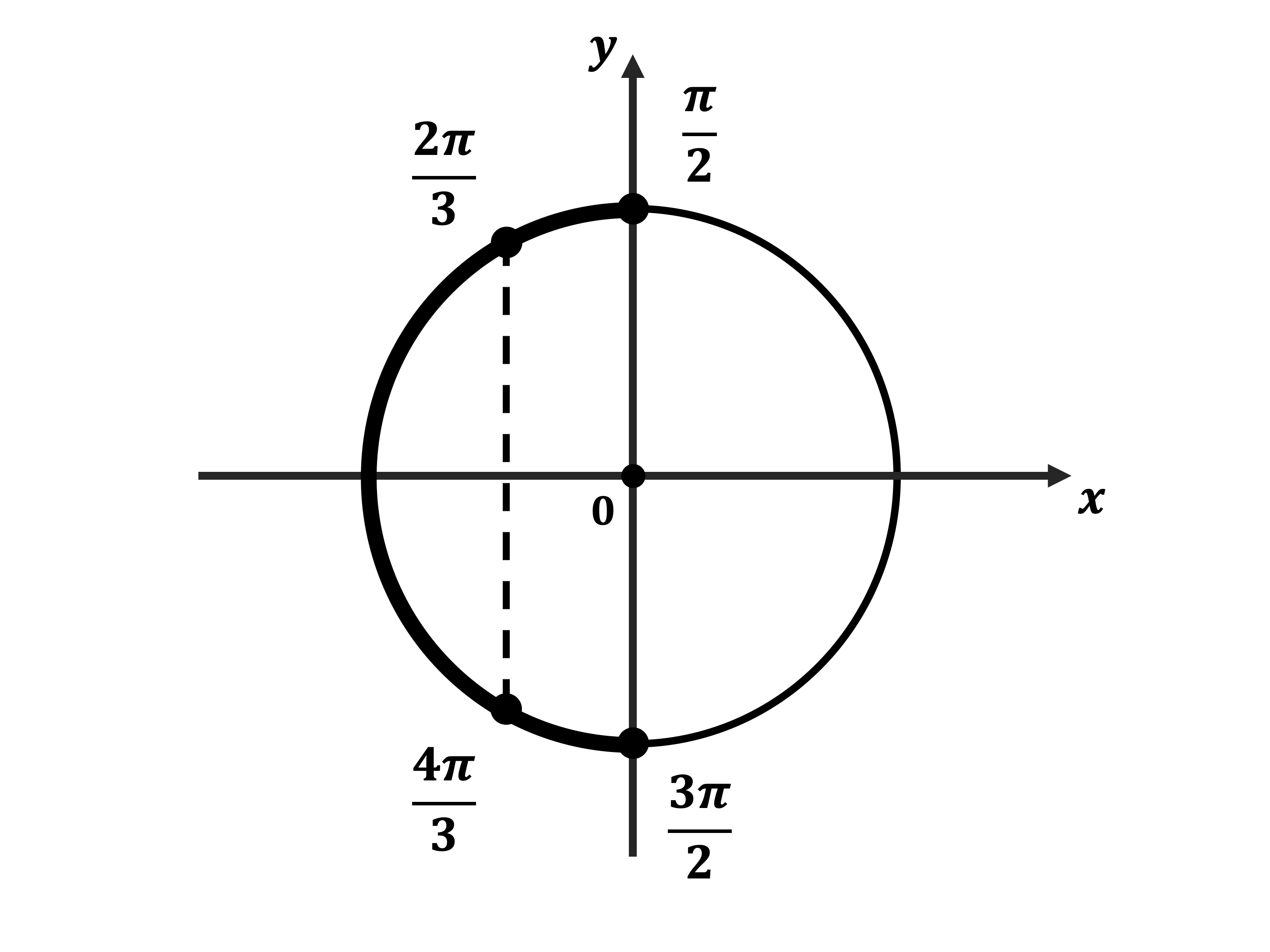
б) Корни, принадлежащие отрезку $[<π>/<2>; <3π>/<2>]$, найдём с помощью единичной окружности. Получим числа $<2π>/<3>; <4π>/<3>$.
Задача 4
а) Решите уравнение $cos(x — <3π>/<2>)= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-<3π>/<2>;0]$.
Решение
а) Преобразуем уравнение:
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
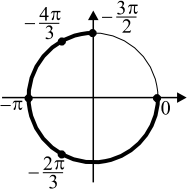
б) Корни, принадлежащие отрезку $[-<3π>/<2>;0]$, найдём с помощью единичной окружности. Получим числа $−<4π>/<3>; −π; −<2π>/<3>; 0$.
Задача 5
а) Решите уравнение $sin(<π>/<2>+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число $<π>/<2>$.
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin <4π>/<3>= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-<π>/<2>;π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin<4π>/ <3>= 0$.
Так как $sin<4π>/ <3>= sin(π +<π>/<3>) = − sin<π>/ <3>= −<√3>/<2>$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-<√3>/ <2>= 0$. Отсюда $2 sin x(sin x-<1>/<2>)+ √3(sin x-<1>/<2>) = 0; (2sinx+√3)(sin x-<1>/<2>) = 0$.
Тогда $sin x = <1>/<2>; x = (−1)^n<π>/ <6>+ πn$ или $sin x = −<√3>/<2>; x = (−1)^
б) Корни, принадлежащие промежутку $[−<π>/<2>; π)$, найдём с помощью числовой окружности: $−<π>/<3>; <π>/<6>; <5π>/<6>$.
Задача 7
а) Решите уравнение $4cos^<2>x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-<5π>/<4>)$.
Решение
a) $4cos^<2>x = 3cos2x+1$,
$cos^<2>x=1, \[\table\cosx=1; \cosx=-1;$ $\[\table\x=2πn, n ∈ Z; \x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-<5π>/<4>)$, найдем из неравенства $-4π ≤ πk ×
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Задание 12 ЕГЭ по математике профильный уровень — уравнения
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
| Источник | Задания |
| math100.ru | Рациональные уравнения Уравнения смешанного типа, содержащие тригонометрические функции |
| vk.com/ekaterina_chekmareva | Скачать задания |
| semenova-klass.moy.su | Скачать уравнения |
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
http://egeturbo.ru/ege/math/tasks/12
http://vpr-ege.ru/ege/matematika/1709-zadanie-12-ege-po-matematike-profilnyj-uroven-uravneniya