Задание 13 485973 а решите уравнение

ЕГЭ профильный уровень. Задания №13. Решение уравнений.

ЕГЭ профильный уровень. Задания №13. Представлены 10 уравнений с решениями.

Использовались материалы сайта http://self-edu.ru

Просмотр содержимого документа
«ЕГЭ профильный уровень. Задания №13. Решение уравнений.»

ЕГЭ 2019 ПРОФИЛЬНЫЙ УРОВЕНЬ

ЗАДАНИЕ №13 с решениями

Использовались материалы сайта http://self-edu.ru

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Преобразуем выражение:

Получаем два уравнения:

и вторая серия решений

б) Используя неравенства, получаем корни, принадлежащие диапазону .

Для :

имеем целое значение n=-1 и корень ;

Для :

целых значений m нет.

Для :

имеем одно целое значение k=0 и корень .

Ответ: а) ;; ; б) .

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку [-2; 0].

а) Преобразуем выражение:

Так как основания логарифмов одинаковы, то можно перейти к равенству подлогарифмических выражений:

Сделаем замену , получим:

Обратная подстановка дает следующие корни:

и

б) Промежутку [-2;0] удовлетворяют корни .

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Преобразуем выражение:

Сделаем замену , получим:

Обратная подстановка дает уравнения:

б) Выберем корни, принадлежащие диапазону . Очевидно, что это значения .

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Преобразуем выражение:

Делаем замену , получим:

Обратная подстановка дает два уравнения:

б) Так как , а имеем промежуток и с помощью неравенств определяем корни, принадлежащие этому промежутку.

целые значения n=1 и корень .

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) 1. Запишем ОДЗ уравнения:

2. Перепишем уравнение в виде:

3. Совместно с ОДЗ, получаем систему:

Решаем последнее квадратное уравнение:

4. Проверяем принадлежность корней к ОДЗ:

Имеем только один корень , который принадлежит ОДЗ.

б) Проверим, попадает ли значение 1/2 в диапазон :

Последнее неравенство показывает, что число 1/2 не принадлежит диапазону .

Ответ: а) 1/2; б) нет.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Преобразуем выражение:

Получаем два уравнения:

б) Используя неравенства, получаем корни, принадлежащие диапазону .

имеем целые значения n=-1; 0 и корни .

имеем целое значение m=0 и корень .

целых значений k нет.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку (0; 2)

а) Преобразуем выражение:

Сделаем замену , получим:

Обратная подстановка дает два уравнения:

б) Найдем корни, которые принадлежат диапазону (0; 2). Значение -1 не принадлежит этому диапазону. Проверим второй корень:

принадлежит промежутку (0; 2).

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие промежутку (-90°; 180°)

а) Рассмотрим два случая исходного уравнения:

Случай 1. при . Получаем уравнение:

Делаем замену , получим:

Обратная подстановка второго корня дает уравнение:

Эта серия решений принадлежит диапазонам .

Случай 2. при . Получаем уравнение:

Делаем замену , имеем:

Обратная замена дает уравнение:

Эта серия решений принадлежит диапазонам .

б) С помощью единичной окружности найдем корни, принадлежащие диапазону (-90°; 180°):

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Запишем ОДЗ для уравнения:

Делаем замену: , получим:

Обратная подстановка дает два уравнения:

решение принадлежит ОДЗ

решение принадлежит ОДЗ

б) С помощью единичной окружности найдем корни, принадлежащие диапазону :

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

а) Преобразуем выражение:

б) Используя неравенства, получаем корни, принадлежащие диапазону .

Задание 13. Задача на стереометрию. ЕГЭ 2022 по математике профильного уровня

Что нужно знать, чтобы решить задание 13:

В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.

Задачи для практики

Задача 1

Дан куб $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $M$, причём $AM:MA_1=1:1$, на ребре $BB_1$ отмечена точка $N$,
причём $BN:NB_1=1:2$, на ребре $CC_1$ отмечена точка $K$, причём $CK:KC_1=1:3$.
а) В каком отношении, считая от точки $D$, плоскость $MNK$ делит ребро $DD_1$?
б) Найдите величину угла между плоскостями $MNK$ и $ABC$.

Решение

а) Пусть ребро куба равно $1$. Противоположные грани куба параллельны, поэтому плоскость $MNK$ пересекает их по параллельным отрезкам. Сечением куба плоскостью $MNK$ является параллелограмм $MNKF$, где $F$ — точка пересечения ребра $DD_1$ с плоскостью $MNK$. Рассмотрим проекцию куба на грань $CC_1D_1D$. $DM_1=AM$, $CN_1=BN$. Отрезки $M_1N_1$ и $FK$ параллельны, поэтому $N_1K= <1>/ <3>— <1>/ <4>= <1>/ <12>$, и $FD=M_1D-M_1F= <1>/ <2>— <1>/ <12>= <5>/ <12>$, значит, $DF:FD_1=5:7$. б) Прямая $FK$ пересекает плоскость основания куба в точке $L$, прямая $NK$ пересекает плоскость основания куба в точке $T$, поэтому плоскость $MNK$ пересекает плоскость $ABC$ по прямой $TL$. В прямоугольном треугольнике $CLT$ отрезок $CH$ — высота, по теореме о трёх перпендикулярах $KH⊥ TL$, поэтому линейный угол $CHK$ является углом между плоскостями $MNK$ и $ABC$. Треугольники $CLK$ и $DLF$ подобны, $CK= <1>/ <4>$, $FD= <5>/ <12>$, $DL=1+CL$, тогда из пропорции $ <1>/ <4>: <5>/ <12>=CL:(1+CL)$, получим $CL= <3>/ <2>$. Аналогично из подобия треугольников $CTK$ и $BTN$ найдём $CT=3$. В прямоугольном треугольнике $CLT$ гипотенуза $LT$ вычисляется по теореме Пифагора:$LT= <3√ 5>/ <2>$, а высота $CH= / = <3>/ <√ 5>$. В прямоугольном треугольнике $CHK$ вычисляем
$\tg∠ CHK= / = <1>/ <4>: <3>/ <√ 5>= <√ 5>/ <12>$, значит, $∠ CHK=\arctg <√ 5>/ <12>$.

Задача 2

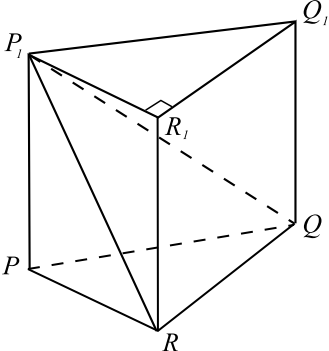
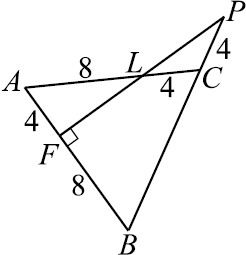
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.

Решение

По условию задачи сделаем чертёж.

а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$

б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен $/<3>$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен $/<3>$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен $/<3>$.

В призме $PQRP_1Q_1R_1 : QQ_1 = √ = 3√21, QR = √ = 8, PR = √ = 6, V = PP_1 · / <2>= 72√21$.

Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.

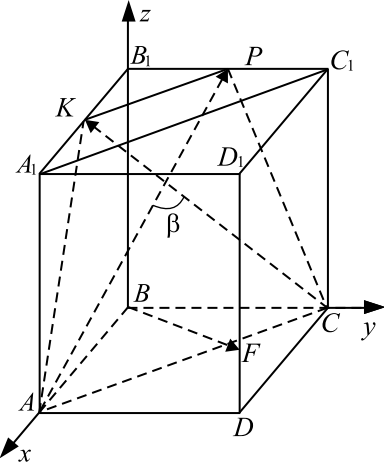
Задача 3

В правильной четырёхугольной пирамиде $SABCD$ боковое ребро $SA=12$, а высота равна $4$. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $E$, $F$ и $K$ соответственно, причём $BE=CF=12$, $AK=3$.
а) Докажите, что плоскости $SBC$ и $KEF$ параллельны.
б) Найдите объём пирамиды $KSBC$.

Решение

а) Докажем, что плоскости $SBC$ и $KEF$ параллельны.

Введём прямоугольную систему координат, учитывая, что в основании правильной пирамиды квадрат $ABCD$ и угол между диагоналями квадрата прямой .

1. Найдём координаты точек $S, B, C , K , E, F$. В прямоугольном треугольнике $SOA$ по теореме Пифагора $OA^2 = SA^2 — SO^2, OA = √ <12^2 - 4^2>= 8√2. OC = OB = OD = OA = 8√2$, тогда сторона квадрата $AB = / = <8√2>/<<1>/<√2>> = 16, AE = AB — BE = 16 — 12 = 4$.

Проведём $KN ‖ SO, SO ⊥ (ABC)$, тогда $KN ⊥ (ABC)$ и $KN ⊥ OA, △SAO ∼ △KAN$ по первому признаку подобия $(∠SOA = ∠KNA = 90°, ∠A$ — общий) $/ = /, <12>/ <3>= <4>/, KN = 1$.

В прямоугольном треугольнике $ANK$ по теореме Пифагора $AN^2 = AK^2 — KN^2, AN = √ <3^2 - 1^2>= 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.

Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.

2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали $↖<→>(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам $↖<→>(0; -8√2; -4)$ и $↖<→>(-8√2; 0; -4)$.

Для плоскости $KEF$, вектор нормали $↖<→>(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам $↖<→>(0; -2√2; -1)$ и $↖<→>(-8√2; 6√2; -1)$.

Её решение $a_2 = <√2>/<4>; b_2 = <√2>/<4>$.$↖<→>(<√2>/<4>; <√2>/<4>; -1)$ — вектор нормали плоскости $KEF$.

Векторы $↖<→>$ и $↖<→>$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.

б) Искомый объём $V = <1>/<3>S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.

2. Чтобы найти $h$ необходимо найти уравнение плоскости $SBC$. Оно имеет вид $ax + by + cz + d = 0$, где $↖<→>(a; b; c)$ — вектор нормали этой плоскости. Согласно пункту а), один из векторов нормали $↖<→>(<√2>/<4>; <√2>/<4>; -1)$. Значит, уравнение имеет вид $<√2>/<4>x + <√2>/<4>y — z + d = 0$. Чтобы найти значение $d$ подставим координаты точки $S(0; 0; 4)$ в это уравнение, получим $-4 + d = 0, d = 4$, тогда $<√2>/<4>x + <√2>/<4>y — z + 4 = 0$ — уравнение плоскости $SBC$. Расстояние от точки $K(6√2; 0; 1)$ до плоскости $SBC$

Задача 4

В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB=8√ <2>$, а боковое ребро $AA_1=16$. Точка $K$ — середина ребра $A_1B_1$. На ребре $DD_1$ отмечена точка $F$ так, что $DF=4$. Плоскость $α$ параллельна прямой $A_1C_1$ и содержит точки $K$ и $A$.
а) Докажите, что прямая $BF$ перпендикулярна плоскости $α$.
б) Найдите объём пирамиды, вершина которой точка $B$, а основание — сечение данной призмы плоскостью $α$.

Решение

1. Построим сечение призмы плоскостью $α$.

Грани $ABCD$ и $A_1 B_1 C_1 D_1$ параллельны, значит плоскость α пересекает их по параллельным прямым.

По условию плоскость α параллельна прямой $A_1 C_1$, то есть содержит прямую, параллельную $A_1 C_1$. Поэтому, проведя через точку $K$ прямую $KP (P ∈ B_1 C_1)$, параллельную прямой $A_1 C_1$, и через точку $A$ — прямую $AC$, параллельную прямой $A_1 C_1$ (прямая $AC$ содержит диагональ нижнего основания) получим трапецию $AKPC$ — искомое сечение.

2. Выберем прямоугольную систему координат, как показано на рисунке. Найдём координаты нужных точек: $B(0; 0; 0), F (8√2; 8√2; 4), A(8√2; 0; 0), C (0; 8√2; 0), K (4√2; 0; 16), P (0; 4√2; 16)$.

3. Рассмотрим векторы $↖ <→>(8√2; 8√2; 4), ↖ <→>(-8√2; 4√2; 16)$ и $↖ <→>(4√2; -8√2; 16)$.

Отсюда следует, что $BF ⊥ α$ по признаку перпендикулярности прямой и плоскости ($BF$ перпендикулярна двум пересекающимся прямым плоскости).

б) Искомый объём $V = <1>/<3>S · h$, где $S$ — площадь четырёхугольника $AKPC$, а высота $h$ — расстояние от точки $B$ до плоскости $α$.

1. $S_ = <1>/<2>AP · CK sin β$, где $β$ — угол между диагоналями $AP$ и $CK$ четырёхугольника $AKPC$.

2. Чтобы найти $h$ необходимо найти уравнение плоскости $α$. Оно имеет вид $ax + by + cz + d = 0$, где $↖<→>(a; b; c)$ — вектор нормали этой плоскости.

Согласно пункту а) одним из векторов нормали является вектор $↖<→>(8√2; 8√2; 4)$.

Значит, уравнение плоскости имеет вид $8√2x + 8√2y + 4z + d = 0 (1)$.

Чтобы найти значение $d$ подставим координаты точки $A(8√2; 0; 0)$ в уравнение (1) и получим $8√2 · 8√2 + d = 0, d = -128$.

Уравнение плоскости $α$ примет вид $8√2x + 8√2y + 4z — 128 = 0$.

Найдём расстояние $h$ от точки $B(0; 0; 0)$ до плоскости сечения.

Задача 5

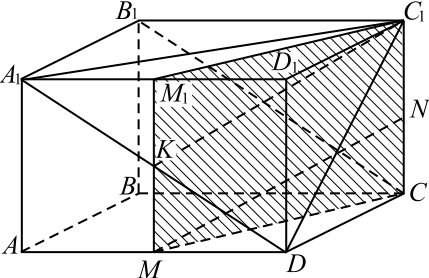
В прямоугольном параллелепипеде $ABCDA_<1>B_<1>C_<1>D_<1>$ сторона $AB=AA_<1>=3$, $AD=6$. На рёбрах $AD$ и $CC_<1>$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_<1>C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_<1>$.

Решение

а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$

Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)

Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$

Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения

Таким образом, $A_1 C_1 D$ — искомое сечение.

б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.

Задача 6

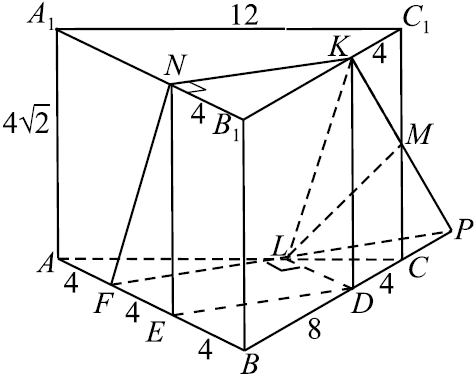
В правильной треугольной призме $ABCA_1 B_1 C_1$ сторона основания равна $12$, а боковое ребро равно $4√ <2>$. На рёбрах $AB$, $A_1 B_1$ и $B_1 C_1$ отмечены точки $F$, $N$ и $K$ соответственно, причём $AF=B_1 N=C_1 K =4$.
а) Пусть $L$ — точка пересечения плоскости $FNK$ с ребром $AC$. Докажите, что $FNKL$ — ромб.
б) Найдите площадь сечения призмы плоскостью $FNK$.

Решение

а) Докажем, что $FNKL$ — ромб.

1) Так как точка $L$ — точка пересечения плоскости $FNK$ с ребром $AC$, то (по свойству параллельных плоскостей) линии пересечения плоскости $FNK$ с основанием призмы параллельны, т.е $FL ‖ N K$.

2) В основаниях правильной треугольной призмы лежат правильные треугольники со стороной $12$.

В треугольнике $NB_1K$ $∠B1 = 60°, NB_1 = 4$ по условию, а $B_1 K = 12 — 4 = 8$. По теореме косинусов $N K = 4√3$, поэтому $N K^2 + NB_1^2 = KB_1^2$. Отсюда следует, что $∠N = 90°, ∠K = 30°$.

Значит, $N K ⊥ A_1B_1$ и $F L ⊥ AB$, т.к. $N K ‖ F L$, а $A_1B_1 ‖ AB$.

3) В $△AFL$ $∠A = 60°, ∠F = 90°, AF = 4$;

$AF$ в прямоугольном $△AFL$ лежит против $∠L = 30°$, следовательно, $AF = <1>/<2>AL, AL = AF · 2 = 4 · 2 = 8$;

$FL^2 = AL^2 — AF^2 = 8^2 — 4^2 = 64 — 16 = 48, F L = 4√3$.

Имеем $N K ‖ F L$ и $N K = F L$, следовательно $F N K L$ — параллелограмм.

Проведём $N E ⊥ F B$.

В $△NFE$ $∠E = 90°, N E = 4√2, F E = 12 — 8 = 4$.

$FN^2 = NE^2 + FE^2 = (4√2)^2 + 4^2 = 32 + 16 = 48$,

$FN = √48 = 4√3, KL = FN$ как противоположные стороны параллелограмма.

4) Имеем: $N K = K L = F N = F L$, следовательно, $F N K L$ — ромб.

б) $K N ⊥ A_1B_1 , K N ⊥ N E ⇒ K N ⊥ (AA_1B_1)$ и $K N ⊥ F N$, значит $K N F L$ — квадрат, $S_ = FN^2 = 48$.

Построим сечение пирамиды плоскостью $FNK$ .

Продлим $FL$ до пересечения с $BC$, получим точку $P$.

Соединим точку $P$ с точкой $K$, $KP$ пересекает $CC_1$ в точке $M$. Соединим точку $M$ с точкой $L$.

Пятиугольник $F N K M L$ — искомое сечение.

В прямоугольном $△FBP$ $∠B = 60°$, значит $BP = 2FB = 16, PC = 16 — 12 = 4$.

$KC_1 = CP, ∠KC_1M = ∠MCP = 90°$, тогда $△KC_1M = △PCM$ и $C_1M = CM = 2√2. KM = √ <4^2 + (2√2)^2>= √<24>$. В $△LMC$ $LM^2 = LC^2 + MC^2, LC = AC — AL = 12 — 8 = 4, MC = <1>/<2>CC_1 = 2√2, √ <4^2 + (2√2)^2>= √<24>, K L = √<48>$, следовательно, $△KLM$ прямоугольный, $S_ = <1>/<2>(√<24>)^2 = 12$.

$S_ <сеч>= S_ + S_ = 48 + 12 = 60$.

Задача 7

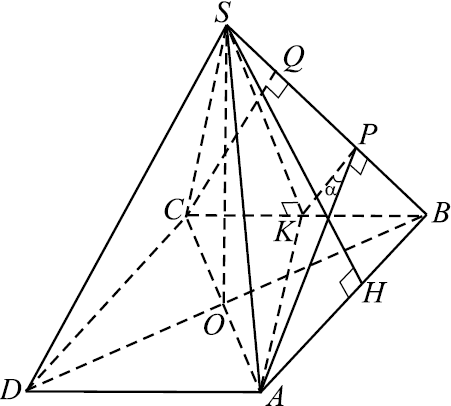
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ <2>$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.

а) Докажите, что точка $P$ является серединой отрезка $BQ$.

б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.

Решение

а) Пусть боковое ребро $SB$ равно $x$.

1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда $/ = /$. $H$ — середина $AB$. Тогда $/ <3>= <6>/; PB = <18>/$.

2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда $/ = /; / <3√2>= <6√2>/; QB = <36>/$.

б) 1) Из пункта а) следует, что $PK$ — средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ — линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.

3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = <36>/ = <36>/<12>=3$.

Так как $PK$ — средняя линия, то $PK = <1>/<2>CQ = <3√7>/<2>$.

5) По теореме косинусов для $△APK$:

$AK^2 = AP^2 + PK^2 — 2·AP·PK·cosα$;

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.

Статистика

Задание №13 является мостиком между 1 и 2 частями и от ее выполнения часто зависит, сможешь ли ты набрать выше 70 баллов, для многих это решающие баллы при получении золотой медали, так или иначе эти 2 первичных балла – фундамент для поступления, особенно на бюджет.

Алгоритм решения задания №13

1. Находить ОДЗ — область допустимых значений переменной. Например, если мы видим в задаче √x, нужно отметить, что x⩾0. Также нужно быть аккуратным с логарифмами, знаменателем, tg(x) и ctg(x), которые существуют не при всех значениях переменной x.
2. Хорошо знать тригонометрию. В 95% случаев на ЕГЭ дают либо чисто тригонометрическое уравнение, либо уравнение смешанного типа, в котором присутствует тригонометрия.

Что тебе точно пригодится: табличные значения, формулы приведения, знаки тригонометрических функций, решение простейших тригонометрических уравнений, формулы двойного аргумента, синус и косинус суммы (разности), основное тригонометрическое тождество.
Сделать замену. Большинство уравнений сводится к замене. Например, если перед тобой уравнение:

Пример

Как было отмечено ранее, сделаем замену и решим квадратное уравнение для новой переменной:

Оба корня получились неотрицательными, значит нам подойдут Сделаем обратную замену и найдем решения для исходной переменной:

В пункте (а) рисовать окружность не обязательно, здесь она приведена только для вашего удобства. Вот мы и набрали 1 балл, теперь давайте воспользуемся способом отбора корней при помощи единичной окружности и заработаем максимальное количество баллов за задачу.

Давайте разберем критерии такого отбора. Это очень важно, потому что при их невыполнении эксперт может посчитать отбор недостаточно обоснованным:

Критерии отбора корней с помощью окружности

1. Отметь на окружности граничные точки
2. Заштрихуй область об меньшего значения к большему (против часовой стрелки)
3. Отметь все подходящие корни на окружности и обязательно подпиши их значения. Желательно отдельно распиши, как ты их получил.

Вот тебе аналогичный пример для решения дома, потренируйся и я уверен, что практика задания 13 принесет тебе 2 балла на экзамене.

Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath

Задание №13 ЕГЭ по математике профильного уровня

Уравнения

В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.

Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант2018)

Алгоритм решения:

1. При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
2. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
3. Делаем обратную замену и решаем

Простейшие (Protozoa) — тип одноклеточных животных.

1. Строим числовую ось.
2. Наносим на нее корни.
3. Отмечаем концы отрезка.
4. Выбираем те значения, которые лежат внутри промежутка.
5. Записываем ответ.

Решение:

сos2x = 1 – sin x.

Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:

Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:

3. Делаем обратную замену:

Решаем эти уравнения:

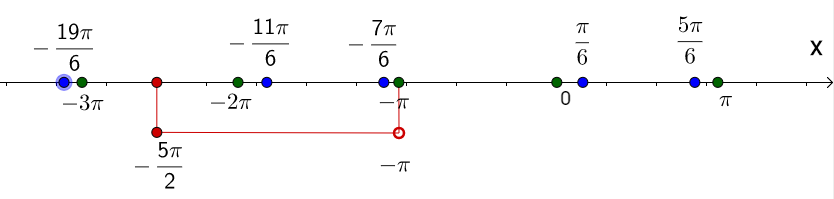
Следовательно, получаем два семейства решений. Пункт б):

1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.

2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).

3. Красным цветом помечаем концы промежутка. 4. В указанном промежутке расположены три

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Второй вариант задания (из Ященко, №1)

Алгоритм решения:

1. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
2. Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.

1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка.
4. Записываем ответ.

Решение:

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

D=b 2 – c = 81 – 4∙4∙2 =49,

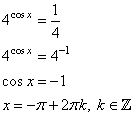
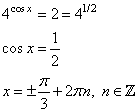
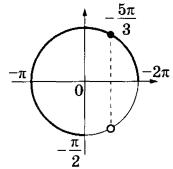
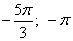
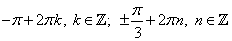
3. Возвращаемся к переменной х: Пункт б) 1. Строим координатную плоскость и окружность единичного радиуса на ней. 2. Отмечаем точки, являющиеся концами отрезка. 3. Выбираем те значения, которые лежат внутри отрезка.. Это корни . Их два. Ответ: а) б)

Третий вариант задания (из Ященко, № 6)

Алгоритм решения:

1. При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
2. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
3. Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.

1. Решаем неравенства для каждого случая.
2. Записываем ответ.