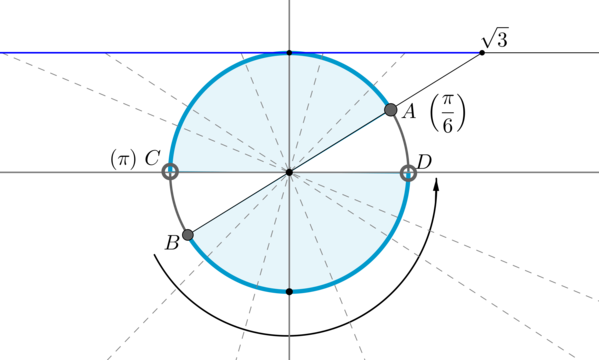
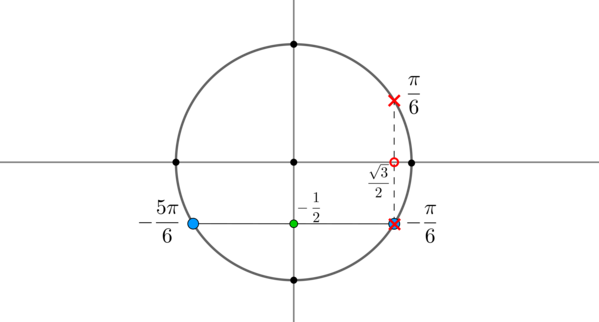
Решение тригонометрического уравнения. Задание 5
Решение тригонометрического уравнения. Задание 5
В этой статье я покажу решение тригонометрического уравнения из Задания 5:
Задание 5 (№ 12889)
Найдите корень уравнения 
Рекомендую вам сначала вспомнить, как решаются простейшие тригонометрические уравнения, затем попробовать решить задачу самостоятельно и сверить свое решение с ВИДЕОУРОКОМ:
И еще одно видео на эту тему:
И.В. Фельдман, репетитор по математике.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Из определения косинуса следует, что \( -1 \leqslant \cos \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.
Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a
Уравнение sin(х) = а
Из определения синуса следует, что \( -1 \leqslant \sin \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.
Уравнение sin х = а, где \( |a| \leqslant 1 \), на отрезке \( \left[ -\frac<\pi><2>; \; \frac<\pi> <2>\right] \) имеет только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале \( \left( -\frac<\pi><2>; \; \frac<\pi> <2>\right) \) только один корень. Если \( |a| \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right) \); если а
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0
Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y1 = -3, y2 = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; \( x = (-1)^n \text
Ответ \( x = (-1)^n \frac<\pi> <6>+ \pi n, \; n \in \mathbb
Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0
Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y1 = 1, y2 = 1/3
Уравнение вида a sin(x) + b cos(x) = c
Решить уравнение 2 sin(x) + cos(x) — 2 = 0
Используя формулы \( \sin(x) = 2\sin\frac
Поделив это уравнение на \( \cos^2 \frac
Обозначая \( \text
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, \( \sqrt
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0
Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0
Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0
Простейшие тригонометрические уравнения (задание 5) и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).
Рассмотрим несколько примеров:
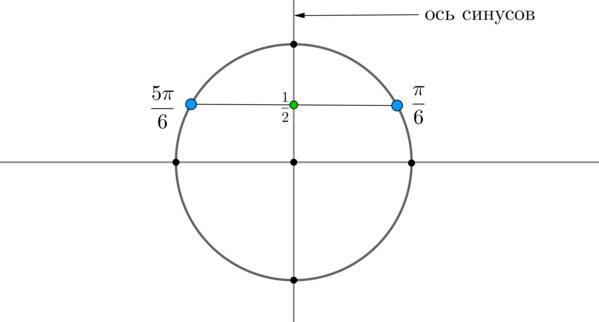
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb
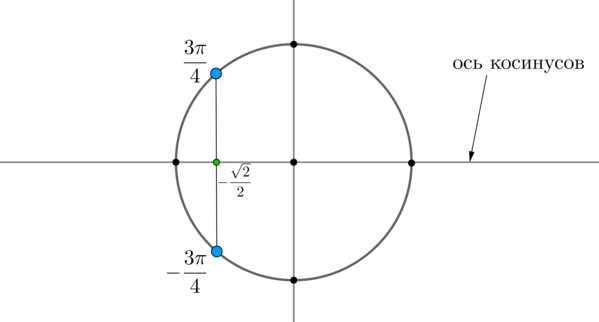
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .
Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.
Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb
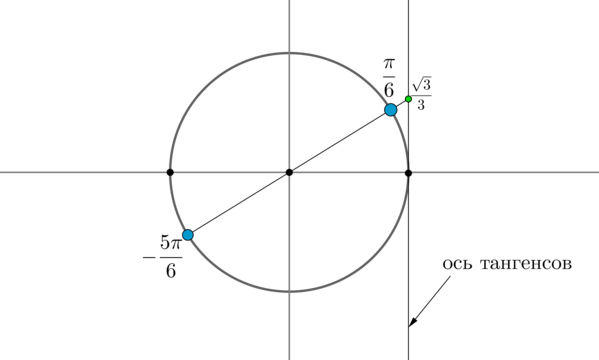
Пример 3. Решить уравнение \(\mathrm
Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .
Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb
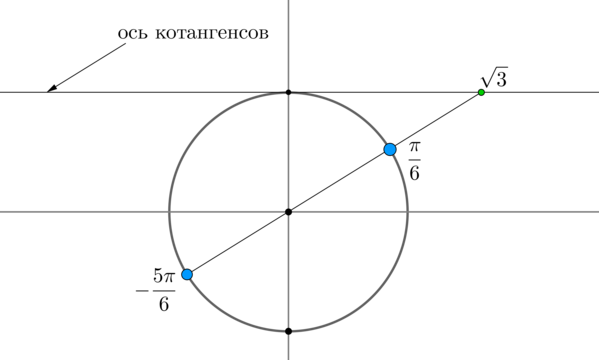
Пример 4. Решить уравнение \(\mathrm
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .
Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin
\(\blacktriangleright\) Любые уравнения вида \(\mathrm
Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .
Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb
Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb
Рассмотрим данную ситуацию на примере:
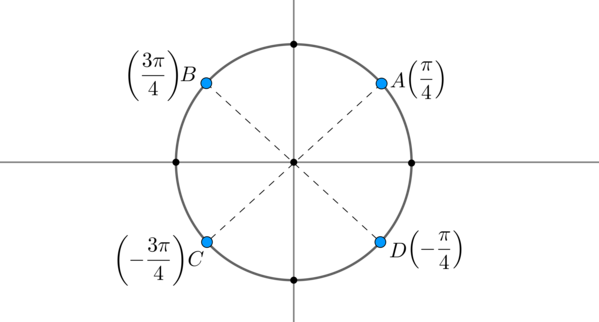
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb
Заметим, что длины дуг \(\buildrel\smile\over
где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .
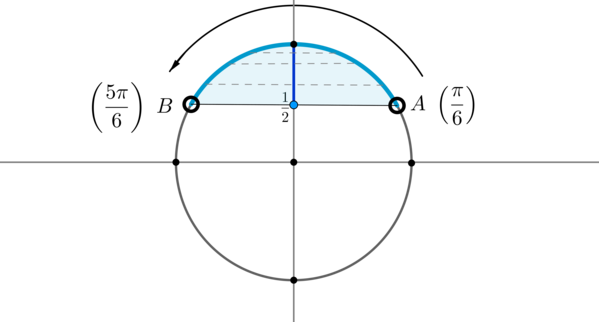
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .
Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb
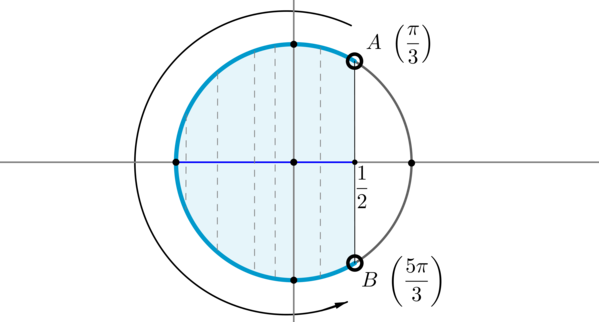
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .
Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb
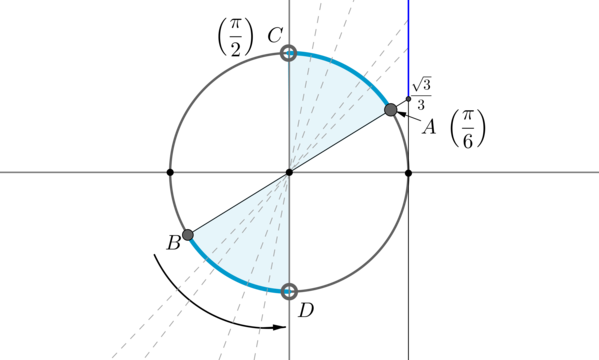
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm
Для начала отметим на окружности корни уравнения \(\mathrm
Рассмотрим одну из дуг, например, \(\buildrel\smile\over
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm
Для начала отметим на окружности корни уравнения \(\mathrm
Рассмотрим одну из дуг, например, \(\buildrel\smile\over
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin
Пример 12. Решить систему \(\begin
Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb
\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .
Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb
\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :
Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]
Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .
Ответ: \((-5p-1; 3p+1), p\in\mathbb
Перейдем к примеру:
Пример 14. Решить систему \[\begin
Решим первое уравнение системы:
\[\left[ \begin
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac
Если \(m=2p+1\) , то \(\frac
Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb
Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb
http://www.math-solution.ru/math-task/trigonometry-equality
http://shkolkovo.net/theory/25