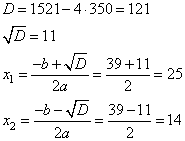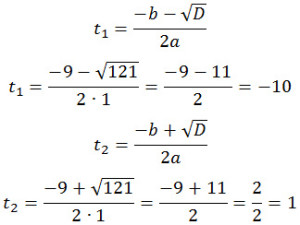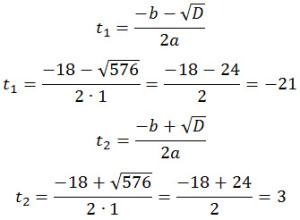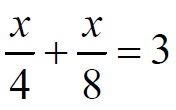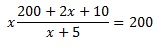Образцы заданий № 4 ОГЭ (ГИА-9) Модуль «алгебра»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Образцы заданий № 4
Автор учитель математики
Чагина Юлия Анатольевна
1. 4 № 85. Найдите корни уравнения 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
2. 4 № 311469. Решите уравнение 
3. 4 № 338480. Решите уравнение
4. 4 № 338488. Решите уравнение
5. 4 № 338495. Решите уравнение
6. 4 № 338500. При каком значении 


7. 4 № 338509. Решите уравнение
8. 4 № 338527. Решите уравнение
9. 4 № 338557. Решите уравнение
10. 4 № 338560. Решите уравнение
11. 4 № 338606. Решите уравнение
12. 4 № 338610. Решите уравнение
13. 4 № 338658. Решите уравнение
14. 4 № 338868. Решите уравнение
Если корней несколько, запишите их в ответ в порядке возрастания, через точку с запятой.
1. 4 № 137381. Решите уравнение 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
2. 4 № 137382. Решите уравнение 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
3. 4 № 137383. Решите уравнение 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
4. 4 № 311405. Найдите корни уравнения 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. 4 № 311446. Найдите корни уравнения 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
6. 4 № 311951. Решите уравнение ( x + 2) 2 = ( x − 4) 2 .
7. 4 № 314495. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
8. 4 № 314538. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
9. 4 № 320540. Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C .
10. 4 № 320541. На рисунке изображены графики функций 

Запишите координаты в ответе через точку с запятой.
11. 4 № 338180. Уравнение 
12. B 4 № 338202. Квадратный трёхчлен разложен на множители: 
13. 4 № 338494. Решите уравнение
14. 4 № 338518. Решите уравнение
15. 4 № 338526. Решите уравнение
16. 4 № 338915. Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
1. 4 № 311381. Решите уравнение: 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
2. 4 № 311393. Решите уравнение 
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
3. 4 № 311755. Решите уравнение
4. 4 № 316225. Решите уравнение:
5. 4 № 316341. Решите уравнение:
6. 4 № 338483. Решите уравнение
7. 4 № 338503. Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
8. B 4 № 338583. Решите уравнение
9. 4 № 338723. Решите уравнение
10. 4 № 338805. Решите уравнение
11. 4 № 338937. Решите уравнение
1. 4 № 311315. Решите систему уравнений
В ответе запишите сумму решений системы.
2. 4 № 311327. Решите систему уравнений
В ответе запишите сумму решений системы.
3. 4 № 311338. Решите систему уравнений
В ответе запишите сумму решений системы.
4. 4 № 311350. Решите систему уравнений
В ответе запишите сумму решений системы.
5. 4 № 311360. Решите систему уравнений
В ответе запишите сумму решений системы.
6. 4 № 311370. Решите систему уравнений
В ответе запишите сумму решений системы.
1. 4 № 314489. Найдите наибольшее значение x , удовлетворяющее системе неравенств
2. 4 № 314490. Найдите наибольшее значение 
3. 4 № 314543. Найдите наибольшее значение 
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m
4) (ab) n = a n b n
7) a n > 1, если a > 1, n > 0
8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.
Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2
Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^
x — 2 = 0
Ответ х = 2
Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Задание №21 ОГЭ по математике
В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста. 2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км |
| 1 велосипедист | 21 | На 2 ч раньше всех |
| 2 велосипедист | 15 | На 1 ч раньше третьего |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя 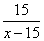
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через 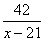
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
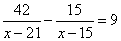
Преобразуем полученное уравнение:
6. Получили квадратное уравнение. Решим его:
По условию скорость третьего велосипедиста была наибольшей, значит, второй
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 15 | t +7 |
| 2 велосипедист | 10 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
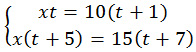

Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t 2 + 19t = 10t + 10
По формуле дискриминанта и корней:
D = 9 2 — 4·1·(-10) = 81 + 40 = 121
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста. 2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 24 | t +9 |
| 2 велосипедист | 21 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км. Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км. Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1). Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км. Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км. Расстояния одинаковы. Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11) Составим систему уравнений для решения задачи: 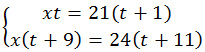
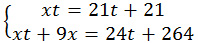
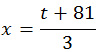
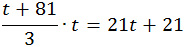
t 2 + 81t = 63t + 63
t 2 + 18t – 63 = 0
D = 18 2 — 4·1·(-63) = 324 + 252 = 576
Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит, 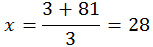
pазбирался: Даниил Романович | обсудить разбор | оценить
Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
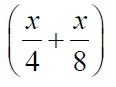
Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
Решая уравнение, получаем x = 8.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
- Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
- Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:
В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.
Тогда обозначим искомую массу через Х и составим пропорцию: 4,2 кг – 70% Х – 100%
Решим эту пропорцию:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
- Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
- Решаем систему.
Решение:
Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).
Через каждую из труб должно пройти 200 л воды. Для 1-й трубы получим:
Аналогично для 2-й трубы:
Из уравнения для 2-й трубы выразим t через х:
Подставим полученное для t выражение в уравнение для 1-й трубы: 
Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).
Значит, искомая скорость наполнения равна 20 л/мин.
pазбирался: Даниил Романович | обсудить разбор | оценить
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800 х . . | 800 |
| 2 автомобиль | х – 36 | 800 х − 36 . . | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800 х − 36 . . − 800 х . . = 5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800х+28800=5х 2 – 180
5х 2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
Решим полученное квадратное уравнение
D=b 2 – 4ac=36 2 – 4 ∙ ( − 5760 ) =24336
х1,2= − b ± √ D 2 a . . = 36 ± 156 2 . .
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
pазбирался: Даниил Романович | обсудить разбор | оценить
http://www.math-solution.ru/math-task/exponential-equality
http://spadilo.ru/zadanie-21-oge-po-matematike/