Задание 9 решите уравнение решу егэ

Задание 9 ЕГЭ по математике. Графики функций

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №9 ЕГЭ.

Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 9 в формате ЕГЭ-2021

Линейная функция

1. На рисунке изображён график функции . Найдите значение , при котором

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

Вычтем из первого уравнения второе:

Уравнение прямой имеет вид:

Найдем, при каком значение функции равно -13,5.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции

Вычтем из первого уравнения второе.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен

Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой

Для точки пересечения прямых:

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть

5. На рисунке изображен график функции . Найдите с.

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид .

6. На рисунке изображён график функции Найдите

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

Формула функции имеет вид:

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому

График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

Найдем абсциссу точки B. Для точек A и B:

(это абсцисса точки A) или (это абсцисса точки B).

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

График функции проходит через точку (2; 1); значит,

График функции проходит через точки (2; 1) и (1; -4), — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда

Для точек A и B имеем:

Отсюда (абсцисса точки A) или (абсцисса точки B).

9. На рисунке изображён график функции . Найдите f (6,76).

Функция задана формулой:

Ее график проходит через точку (4; 5); значит,

10. На рисунке изображен график функции . Найдите .

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда =5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:

Поделим второе уравнение на первое:

Подставим во второе уравнение:

12. На рисунке изображен график функции . Найдите

График функции проходит через точку Это значит, что

формула функции имеет вид: .

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции Найдите

График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

Вычтем из второго уравнения первое:

или — не подходит, так как (как основание логарифма).

14. На рисунке изображен график функции .

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на .

16. На рисунке изображён график функции

На рисунке — график функции Так как

График функции проходит через точку A Подставим и координаты точки А в формулу функции.

Так как получим:

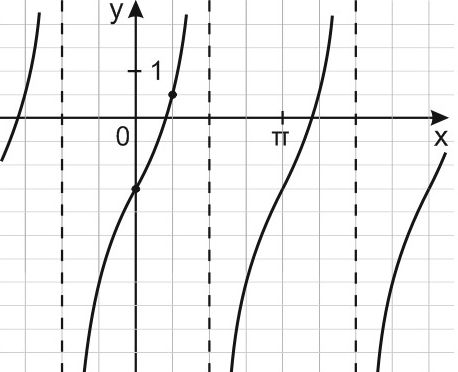
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 9 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Решение Ященко ЕГЭ 2022 (профиль) Вариант №9 (36 вариантов) Математика

Решение и ответы заданий Варианта №9 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.

На некоторые задания буду давать ссылки на решение такого же задания, но с другими числами ( подобное задание). Для решения вам необходимо будет подставить числа из вашего задания.
Делаю это для того, чтобы успеть за этот учебный год решить больше вариантов ЕГЭ. Тем более на экзамене вы должны будете уметь решить задание с любыми числами в условии.
Если какое-то, задание будет не понятно, или этот метод с ссылками на подобные задания вам не удобен, пишите в комментариях под вариантом.

Решено именно это задание из варианта. Решено такое же задание как в варианте, но с другими числами.

Задание 1.
Решите уравнение tg\frac<\pi(2x+5)><6>=\sqrt <3>. В ответе запишите наибольший отрицательный корень.
Ответ задания: –1,5.

Задание 2.
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 10.
Ответ задания: 0,25.

Задание 3.
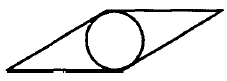
Сторона ромба равна 10, острый угол равен 30°. Найдите радиус окружности, вписанной в ромб.

Ответ задания: 2,5.

Задание 4.
Найдите \frac , если g(x)=\sqrt[3] , при |x| ≠ 10.

Задание 5.
Из единичного куба вырезана правильная четырёхугольная призма со стороной основания 0,4 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Задание 6.
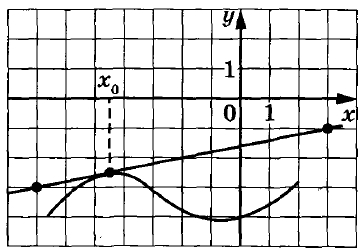
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Ответ задания: 0,2.

Задание 7.
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле A(\omega)=\frac\omega_

^<2>><|\omega_

^<2>-\omega^<2>|> , где ω – частота вынуждающей силы (в с -1 ), A₀ – постоянный параметр, ω_p = 345 с -1 – резонансная частота. Найдите максимальную частоту ω, меньшую резонансной, для которой амплитуда колебаний превосходит величину A₀ не более чем на 12,5%. Ответ дайте в с -1 .
Ответ задания: 115.

Задание 8.
Расстояние между городами А и В равно 180 км. Из города А в город В выехал автомобиль, а через 3 часа следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах.
Ответ задания: 135.

Задание 9.
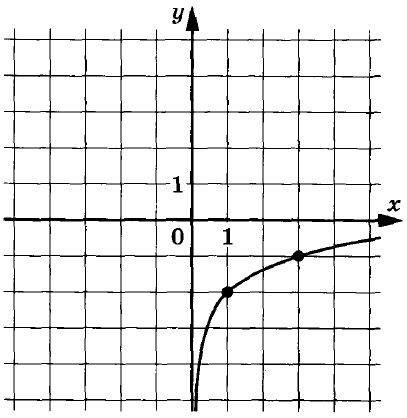
На рисунке изображён график функции f(x) = b + log_aх. Найдите f(81).

Задание 10.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ задания: 0,973.

Задание 11.
Найдите точку максимума функции y = (х + 35)е 35–х .

Задание 12.
а) Решите уравнение 16 + 4 – 3 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5; 5].

Задание 13.
В правильной треугольной призме АВСА₁В₁С₁ точка К – середина ребра АА₁, a АВ = АА₁. Плоскость α проходит через точки К и В₁ параллельно прямой ВС₁.

а) Докажите, что плоскость α делит ребро А₁С₁ в отношении 1:2.
б) Найдите расстояние от точки А₁ до плоскости α, если АВ = 6.

Задание 14.
Решите неравенство 25\cdot 4^<\frac<1><2>-\frac<2>>-133\cdot 10^<-\frac<2>>+4\cdot 5^<1-\frac<4>>\le 0 .

Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 650 тыс. рублей на 10 лет. Условия его возврата таковы:
– в январе 2026, 2027, 2028, 2029 и 2030 годов на сумму 650 тыс. рублей долг возрастает на 19% по сравнению с концом предыдущего года;
– в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.

Задание 16.
В трапеции ABCD основание AD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.

а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.
Ответ задания: 71.

Задание 17.
Найдите все такие значения а, при каждом из которых уравнение

имеет ровно один корень.

Задание 18.
На доске написано 11 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 8, а среднее арифметическое семи наибольших равно 14.

а) Может ли наибольшее из этих одиннадцати чисел равняться 16?
б) Может ли среднее арифметическое всех одиннадцати чисел равняться 10?
в) Найдите наименьшее значение среднего арифметического всех одиннадцати чисел.

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Задание №9 ЕГЭ по математике профильного уровня

Преобразования и вычисления

В задании №9 ЕГЭ по математике профильного уровня нам необходимо выполнить преобразование выражений и произвести элементарные вычисления. Чаще всего в этом разделе встречаются тригонометрические выражения, поэтому для успешного выполнения необходимо знать формулы приведения и другие тригонометрические тождества.

Разбор типовых вариантов заданий №9 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Второй вариант задания (из Ященко, №1)

Алгоритм решения:

1. Преобразуем формулу косинуса двойного угла.
2. Вычисляем косинус.
3. Записываем ответ.

Решение:

Третий вариант задания (из Ященко, №16)

Алгоритм решения:

1. Рассматриваем выражение.
2. Используем свойства тригонометрических функций для определения значений синуса и косинуса заданных углов.
3. Вычисляем значение выражения.
4. Записываем ответ.

Решение:

Четвертый вариант задания (из Ященко)

Алгоритм решения:

1. Анализируем выражение.
2. Преобразовываем и вычисляем выражение.
3. Записываем ответ.

Решение:

1. Выражение содержит два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

2. Преобразовываем выражение и вычисляем его значение:

Ответ: 4.

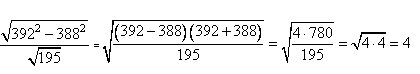
Пятый вариант задания (из Ященко)

Алгоритм решения:

1. Анализируем выражение.
2. Преобразовываем и вычисляем выражение.
3. Записываем ответ.

Решение:

1. Данное выражение представляет собой произведение множителей, которые можно по формулам сокращенного умножения записать в виде разности квадратов: