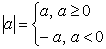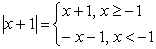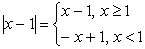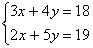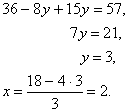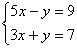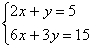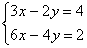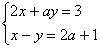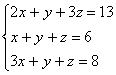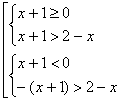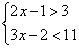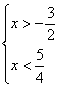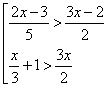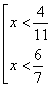Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №42. Линейные уравнения и неравенства с двумя переменными
Перечень вопросов, рассматриваемых в теме:
- Решение уравнений, неравенств, систем уравнений и систем неравенств с двумя переменными;
- Изображение в координатной плоскости множества решений уравнений, неравенств, систем уравнений, систем неравенств;
- Нахождение площади получившейся фигуры.
Глоссарий по теме
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными, где a, b и c — некоторые числа (a ≠ 0 , b ≠0), а, х и у — переменные.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.
В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.
Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: 
. И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.
Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».
1.Найдите уравнения, которые являются линейными.
4х + 5у = 10; 
; у = 7х +4
Ответ: 4х + 5у = 10; 
у = 7х +4
Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.
- Линейные уравнения с двумя переменными.
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.
Если одновременно а 
и b
, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.
Построить график уравнения 2х+у =1
На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.
- Линейные неравенства с двумя переменными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с 0, где х и у – переменные, а, b, c – некоторые числа.
Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.
Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, тк при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.
Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.
Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.
- Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки(- 2; 0) и (0; 3).
- Пусть точка М1(х1,у1) лежит в заштрихованной полуплоскости (ниже прямой 3х – 2у +6 = 0, а М2(х1,у2)лежит на прямой 3х – 2у +6 = 0. Тогда 2у2 – 3х1 – 6 = 0, а 2у1 – 3х1 – 6 0 штриховкой (рис. 1)
Рисунок 1 – решение неравенства 3х – 2у +6 > 0
Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что 
и 
. Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с 0
Чтобы решить неравенство ах + bу + c 0, достаточно взять какую-нибудь точку М1(х1; у1), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх1 + bу1 + c.
«Линейные уравнения и неравенства»
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Просмотр содержимого документа
«»Линейные уравнения и неравенства»»
Линейные уравнения и неравенства
Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска
1. Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение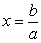 
.
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2=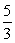
.
Ответ: 0;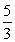 
.
Разложить на множители левую часть уравнения:
х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.
с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.
Ответ: -3; — 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.
Напомним определение модуля числа: 
Например: ½3½=3, ½0½=0, ½- 4½= 4.
В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.
Таким образом, 
Аналогично 
а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х=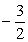
, это число принадлежит множеству х£-1.
b) Пусть -1 х £ 1, тогда данное уравнение равносильно уравнению х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.
с) Рассмотрим случай х1.
х+1+х-1=3, 2х=3, х=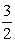
. Это число принадлежит множеству х1.
Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.
Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».
Ответ: [-2; 0]
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.
В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.
Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.
Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.
Если а¹1, а¹-1, тогда уравнение имеет единственное решение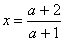 
.
Ответ: если а=1, то х – любое число;
если а=-1, то нет решений;
если а¹±1, то .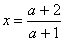
2. Системы уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.
При решении линейных систем используют метод подстановки и метод сложения.
Пример 1. Решить систему уравнений:
Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение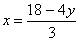 
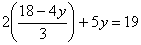
во второе уравнение системы, получим
,
Пример 2. Решить систему уравнений:
Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Пример 3. Решить систему уравнений:
Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.
Пример 4. Решить систему уравнений:
Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.
Пример 5. Решить систему:
Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем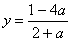 
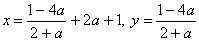
. При а=-2 уравнение не а=-2 имеет решения, если а¹-2, то 
.
Ответ: при a=-2система не имеет решения,
при а¹-2 система имеет решение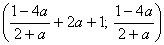 
.
Пример 6. Решить систему уравнений:
Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.
Далее к третьему уравнению системы прибавим второе, умноженное на –3,
наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:
х+у+z=6
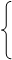
z=3, которая равносильна данной.
Система такого вида называется треугольной.
3. Решение задач с помощью уравнений и систем уравнений.
Покажем на примерах, как можно решать задачи с помощью уравнений и систем уравнений.
Пример 1. Сплав олова и меди массой 32 кг содержит 55% олова. Сколько чистого олова надо добавить в сплав, чтобы в новом сплаве щсодержалось 60% олова?
Решение. Пусть масса олова, добавленная к исходному сплаву, составляет х кг. Тогда сплав массой (32+х)кг будет содержать 60% олова и 40% меди. Исходный сплав содержал 55% олова и 45% меди, т.е. меди в нем было 32·0,45 кг. Так как масса меди в исходном и новом сплавах одна и та же, то получим уравнение 0,45·32=0,4(32+х).
Решив его, находим х=4, т.е. в сплав надо добавить 4 кг олова.
Пример 2. Задумано двузначное число, у которого цифра десятков на 2 меньше цифры единиц. Если это число разделить на сумму его цифр, то в частном получится 4 и в остатке 6. Какое число задумано?
Решение. Пусть цифра единиц есть х, тогда цифра десятков равна х-2 (х2), задуманное число имеет вид 10(х-2)+х=11х-20. Сумма цифр числа х-2+х=2х-2. Следовательно, разделив 11х-20 на 2х-2, получим в частном 4 и в остатке 6. Составляем уравнение: 11х-20=4(2х-2)+6, т.к. делимое равно делителю, умноженному на частное, плюс остаток. Решив это уравнение, получим х=6. Итак, было задумано число 46.
Пример 3. Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в первом, и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?
Решение. Пусть в первом ящике было х орехов, в третьем – y. Тогда во втором ящике было х+0,1х=1,1х или y+0,3y=1,3y. Учитывая, что в первом ящике было на 80 орехов больше, чем в третьем, составляем систему уравнений:
, откуда y=440, х=520, 1,1х=572.
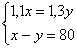
Замечание. Можно эту задачу решить, не составляя системы уравнений. Пусть в первом ящике было х орехов, тогда в третьем — х-80, во втором — 1,1х или 1,3(х-80). Имеем уравнение: 1,1х=1,3(х-80), х=520.
Ответ: в первом ящике было 520 орехов, во втором — 572, в третьем — 440.
Пример 4. Из двух городов А и В, расстояние между которыми 180 км, в 6 ч 20 мин. вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин. Если бы автобус вышел на 1 ч 15 мин. раньше, а легковой автомобиль на 15 мин. позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля?
Решение. Пусть скорость автобуса V1 км/ч, скорость легкового автомобиля V2 км/ч. Так как их встреча произошла через 1,5 ч, то имеем уравнение:1,5V1+1,5V2 =180. Если бы автобус вышел на 1ч 15 мин. раньше, то он был бы в пути 2 ч 30 мин. (7 ч 35 мин. – 5 ч 5 мин.= 2 ч 30 мин.). Если бы легковой автомобиль вышел на 15 мин. позже, то он был бы в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180.
Таким образом, имеем систему двух уравнений с двумя неизвестными:
, откуда V1=40 км/ч, V2=80 км/ч.
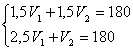
Ответ: 40 км/ч, 80 км/ч.
4. Линейные неравенства с одной переменной.
Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 5х-13х+2. При х=2 получим 5·2-13·2+2 – истинное высказывание (верное числовое высказывание); при х=0 получаем 5·0-13·0+2 – ложное высказывание. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной – значит найти множество всех его решений.
Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяем более простым равносильным ему неравенством и т.д.
Такие замены осуществляются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Линейным называется неравенство вида ax+b0 (соответственно ax+b
Пример 1. Решить неравенство: 2(х-3)+5(1-х)³3(2х-5).
Раскрыв скобки, получим 2х-6+5-5х³6х-15,
-3х-1³6х-15, -9х³-14,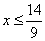 
.
Ответ: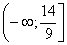 
.
Пример 2. Решить неравенство: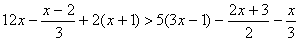 
.
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.
, далее последовательно получаем 
; 
.
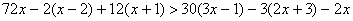
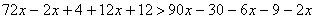
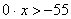
Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая.
Пример 3. Решить неравенство: ½х-1½
На основании определения модуля данное неравенство запишем в виде совокупности двух систем неравенств
(1) 
(2)
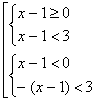
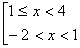
решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).
Пример 4. Решить неравенство:½х+1½2-х.
отсюда х0,5 из первой системы, а вторая система – не имеет решения.
5. Система и совокупности неравенств.
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.
Например: 
Иногда используется запись в виде двойного неравенства. Например, систему неравенств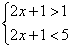 
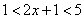
можно записать в виде двойного неравенства 
.
Говорят, что несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множество таких решений, каждое из которых является решением хотя бы одного из этих неравенств.
Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.
Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность. Неравенства, образующие совокупность, иногда объединяются квадратной скобкой. Так, запись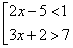 
означает, что неравенства образуют совокупность.
Пример 1. Решить систему неравенств: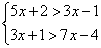 
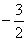
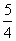
Û 
х
С помощью числовой прямой находим, что пересечением этих множеств служит интервал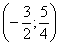 
. Это и есть множество решений данной системы.
Пример 2. Решить совокупность неравенств: 
Преобразовав каждое из неравенств, получим совокупность, равносильную данной 
х
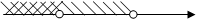
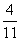
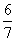
Объединением этих множеств служит промежуток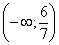 
, который и является решением совокупности неравенств.
Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Неравенства
- Линейные неравенства
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
≥ больше или равно,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x c | x ∈ ( − ∞ ; c ) | |
| x ≤ c | x ∈ ( − ∞ ; c ] | |
| x > c | x ∈ ( c ; + ∞ ) | |
| x ≥ c | Алгоритм решения линейного неравенства
a x b a x ≤ b a x > b a x ≥ b
Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ:
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства Если знак неравенства строгий , Если знак неравенства нестрогий ,
Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
3 ( x + 8 ) − 5 \ x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0
x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств
Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства:
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. источники: http://kopilkaurokov.ru/matematika/uroki/linieinyie-uravnieniia-i-nieravienstva http://epmat.ru/modul-algebra/urok-8-neravenstva-sistemy-neravenstv/ |
