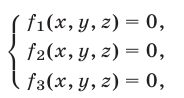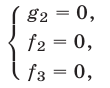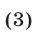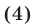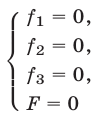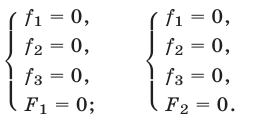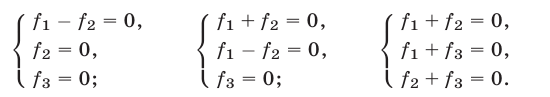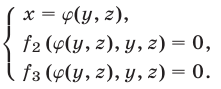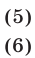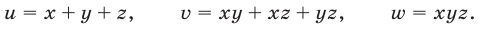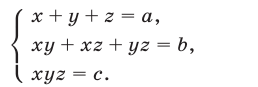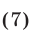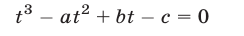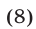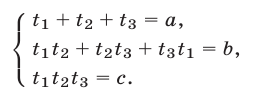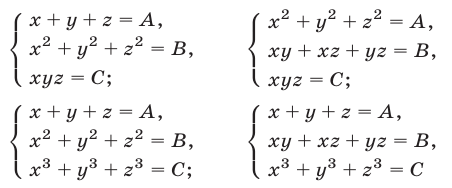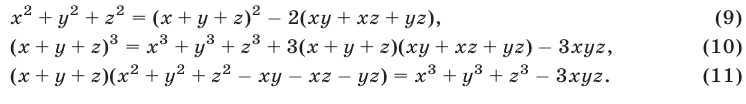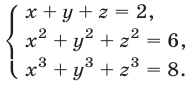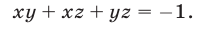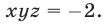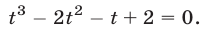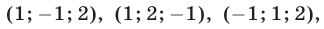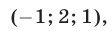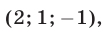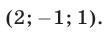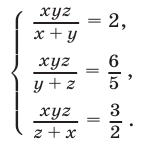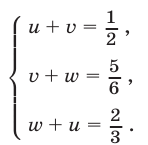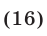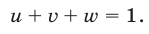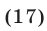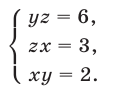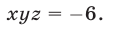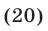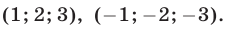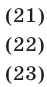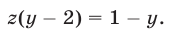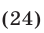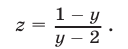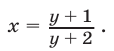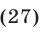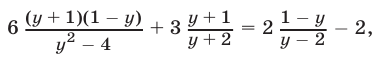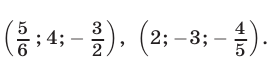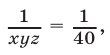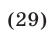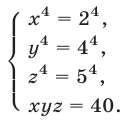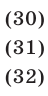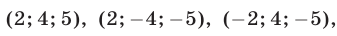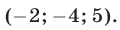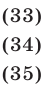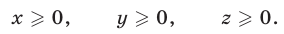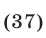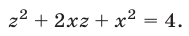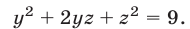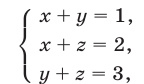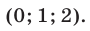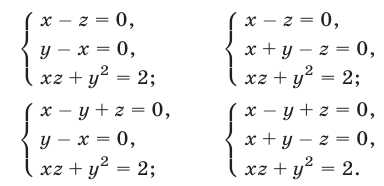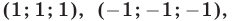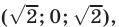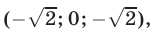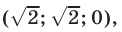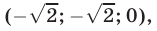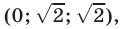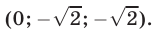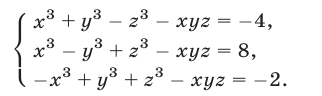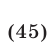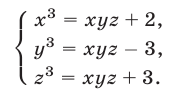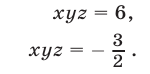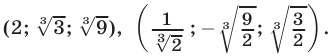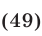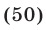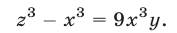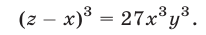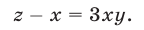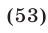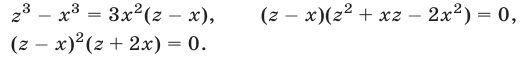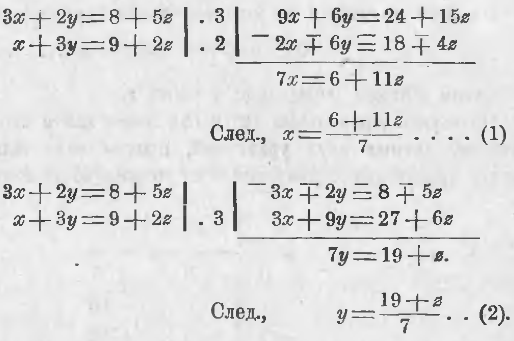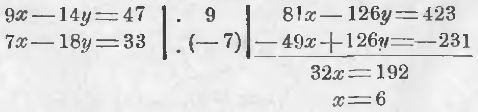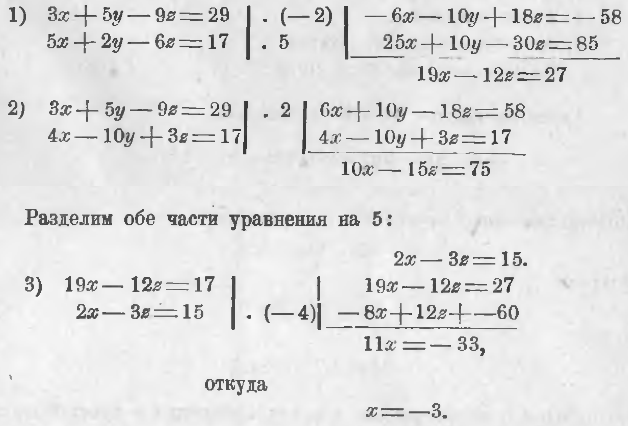Задания с трех уравнений с тремя неизвестными

Алгебраические системы с тремя неизвестными с примерами решения

Алгебраические системы с тремя неизвестными

Для систем с тремя неизвестными определения понятий равносильности и следствия, а также свойства преобразований систем формулируются аналогично тому, как это было сделано для систем с двумя неизвестными.

Будем рассматривать системы вида

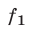
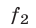
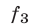
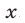
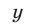
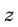
где , , являются либо многочленами от , , , либо могут быть представлены в виде отношения многочленов.

Сформулируем для систем уравнений с тремя неизвестными следующие утверждения, которые могут оказаться полезными при решении систем.

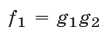
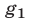
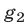
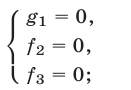
1° Если , где и —многочлены, то система (1) равносильна совокупности систем

и поэтому множество решений системы (1) в этом случае есть объединение множеств решений систем (2) и (3).

2°. Если уравнение

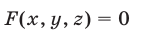
есть следствие системы (1), то система

равносильна системе (1), т. е. при добавлении к системе (1) еще одного уравнения (4), являющегося следствием этой системы, получается система, равносильная системе (1).

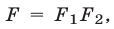
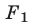
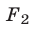
3°. Если уравнение (4) — следствие системы (1), причем где и —многочлены, то система (1) равносильна совокупности систем

4°. Система (1) равносильна каждой из следующих систем:

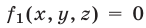
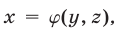
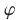
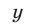
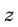
5°. Если уравнение равносильно уравнению где — многочлен от и , то система (1) равносильна системе

Это утверждение лежит в основе метода исключения неизвестных: система (1) сводится к системе (5), (6) с двумя неизвестными.

Прежде чем переходить к примерам алгебраических систем с тремя неизвестными, отметим, что нет общих рецептов для нахождения решений систем. Каждый раз нужно учитывать конкретные особенности рассматриваемой системы. Можно дать только общий совет: решайте побольше задач.

Рассмотрим сначала системы с тремя неизвестными, которые сводятся к кубическим уравнениям.

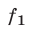
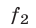
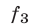
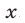
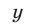
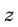
К таким системам относятся системы симметрических алгебраических уравнений, т.е. системы вида (1), где , , — многочлены, каждый из которых не меняется, если поменять местами любую пару из переменных , , .

В этом случае удобно ввести следующие переменные:

Простейший пример системы рассматриваемого вида — система

Система (7) и кубическое уравнение

связаны следующим образом.

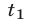
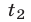
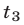
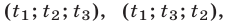
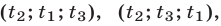
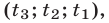
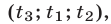
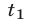
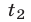
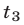
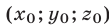
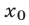
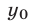
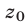
Если , , — корни уравнения (8), то система (7) имеет шесть решений: получаемых всевозможными перестановками трех чисел , , . Обратно, если решение системы (7), то , , — корни уравнения (8).

Доказательство этого утверждения основано на использовании формул Виета для корней уравнения (8):

Для сведения к системам (7) систем симметрических уравнений вида

можно использовать следующие тождества:

Примеры с решениями

Пример №186.

Решить систему уравнений

Решение:

Используя уравнения (12), (13) и тождество (9), получаем

Применяя формулу (11) и учитывая равенства (13)-(15), находим

Следовательно, исходная система равносильна системе вида (7), в которой 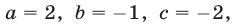, а уравнение (8) имеет вид

Корни этого уравнения — числа 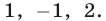Поэтому система имеет шесть решений, получаемых перестановкой чисел

Ответ.

Обратимся теперь к системам с тремя неизвестными, которые не являются симметрическими.

Пример №187.

Решить систему уравнений

Решение:

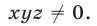
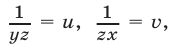
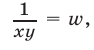
Так как правые части уравнений отличны от нуля, то Полагая получаем систему линейных уравнений

Сложив уравнения системы (16), находим

Из (16) и (17) получаем 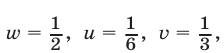т. е.

Перемножив почленно уравнения системы (18), которая равносильна исходной, имеем 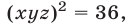откуда

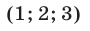
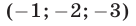
Следовательно, исходная система равносильна совокупности систем (18), (19) и (18), (20), которые имеют решения и соответственно.

Ответ.

Пример №188.

Решить систему уравнений

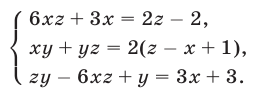
Решение:

Будем решать систему методом исключения неизвестных и сведением, в конечном счете, к одному уравнению с одним неизвестным. Складывая почленно уравнения (21) и (23), получаем

Так как 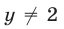на основании равенства (24), то из этого равенства следует, что

Запишем далее уравнение (22) в виде

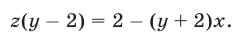
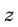
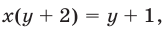
Исключив из уравнений (24) и (26), получаем откуда

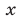
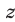
Заметим, что система (27), (25), (21) равносильна системе (21)— (23). Подставляя выражения для и из формул (27) и (25) в уравнение (21), получаем

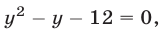
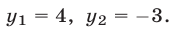
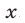
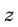
или откуда Соответствующие значения и найдем по формулам (27) и (25).

Ответ.

Пример №189.

Решить систему уравнений

Решение:

Перемножив уравнения системы (28), получаем

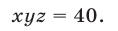
Уравнение (29) является следствием системы (28), которая равносильна системе

Уравнения (30), (31), (32) имеют решения 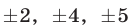соответственно. С учетом равенства (29) находим четыре решения системы (28).

Ответ.

Пример №190.

Найти решения системы уравнений

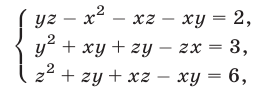
Решение:

Вычитая из уравнения (34) уравнение (33), получаем

Далее, вычитая из уравнения (35) уравнение (33), находим

Наконец, складывая уравнения (34) и (35), получаем

Система (37)-(39) равносильна системе (33)-(35), а при условии (36) — системе линейных уравнений

имеющей единственное решение

Ответ.

Пример №191.

Решить систему уравнений

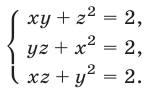
Решение:

Вычтем из уравнения (41) уравнение (40) и преобразуем полученное уравнение к виду

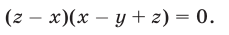
Выполнив ту же операцию с уравнениями (42) и (41), имеем

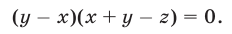
Система (43), (44), (42), равносильная системе (40)-(42), распадается на следующие четыре системы:

Полученные системы легко решаются методом исключения неизвестных. Объединив решения этих систем, найдем все решения исходной системы.

Ответ.

Пример №192.

Решить систему уравнений

Решение:

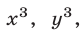
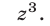
Решим эту систему как линейную относительно Для этого сложим попарно уравнения системы (45) и получим систему

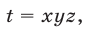
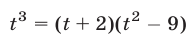
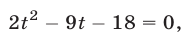
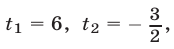
Перемножив уравнения системы (46) и полагая находим или откуда т. е.

Система (45) в силу утверждения 3° равносильна совокупности систем (46), (47) и (46), (48), каждая из которых имеет единственное решение.

Ответ.

Пример №193.

Решить систему уравнений

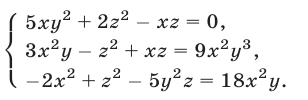
Решение:

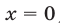
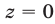
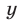
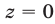
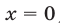
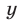
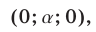
Если , то из системы (49) следует, что , а может принимать любые значения. Аналогично, если , то , — любое. Таким образом, система имеет бесконечное множество решений вида

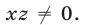
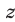
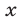
Будем искать решения системы (49) такие, что . Умножив первое уравнение системы (49) на , а третье — на и сложив результаты, получим

Прибавив к уравнению (51) второе уравнение системы (49), умноженное на 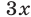:, находим

Каждое из уравнений (51), (52) является следствием системы (49).

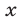
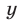
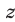
Так как , , — действительные числа (требуется найти действительные решения системы), то уравнение (52) равносильно уравнению

Исключая 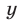из уравнений (53) и (51), получаем

Уравнения (53) и (54) являются следствиями системы (49), а уравнение (54) равносильно совокупности уравнений

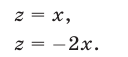
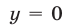
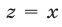
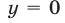
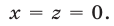
Из (55) и (53) следует, что , а из системы (49) при и находим Полученное решение содержится среди решений (50).

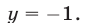
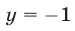
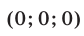
Из (56) и (53) следует, что Подставляя в систему (49), находим решения и

Ответ. 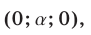— любое действительное число;

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Упражнения. Система линейных уравнений с 3-мя неизвестными.

Эти упражнения позволят проверить, как вы умеете решать системы линейных уравнений с 3-мя неизвестными.

Решение задач и упражнений лучший способ проверить свои знания и закрепить пройденный материал!

Для перехода к следующему заданию нажмите кнопку «Следующий пример».

Внимание. При переходе к новому заданию этот пример станет недоступным.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Математика

64. Три уравнения с тремя неизвестными . Пусть теперь требуется решить совместно 3 уравнения с тремя неизвестными:

3x + 2y – 5z = 8
x + 3y – 2z = 9
4x + 5y – 6z = 26.

Вспоминая все предыдущее, мы уже заранее вправе думать, что здесь произвольные значения ни одному из неизвестных давать нельзя и что здесь найдем единственное решение (по одному числу для каждого неизвестного).

При этом для нас уже намечен путь, как этого достигнуть. В предыдущем п. мы научились из двух уравнений с тремя неизвестными определять два неизвестных через третье. Выберем из наших трех уравнений те два, которые кажутся нам наиболее простыми, напр., 1-е и 2-ое:

3x + 2y – 5z = 8
x + 3y – 2z = 9

и из них определим x и y через z

Подставим теперь полученные выражения для x – a и для y – a в третье уравнение, — получим:

(4(6 + 11z)) / 7 + (5(19 + z)) / 7 – 6z = 26

т. е. получили одно уравнение с одним неизвестным z, которое умеем решить. Сначала освободим его от дробей, для чего обе части его умножим на 7.

4(6 + 11z) + 5(19 + z) – 42z = 182.

24 + 44z + 95 + 5z – 42z = 182.

Перенесем известные члены вправо и сделаем приведение подобных членов:

7z = 63, откуда z = 9.

Теперь из формул (1) и (2) получим:

x = (6 + 11 · 9) / 7 = 15 и y = (19 + 9) / 7 = 4.

2x + 3y = 11
5y + 2z = 3
4z + 3x = 66

Определим из первых двух уравнений 2 неизвестных через третье: мы именно видим, что можно из первого уравнения определить x через y и из второго определить z через y:

x = (11 – 3y) / 2 и z = (3 – 5y) / 2.

Подставим полученные выражения в третье уравнение на место z и x:

(4(3 – 5y)) / 2 + (3(11 – 3y)) / 2 = 66.

4(3 – 5y) + 3(11 – 3y) = 132

12 – 20y + 33 – 9y = 132

x = (11 – 3 · (–3)) / 2 = 10
z = (3 – 5 · (–3)) / 2 = 9.

В этих двух примерах мы держались следующего плана; выбираем из данных трех уравнений какие-либо два, более удобных, и из них определяем два неизвестных через третье, – полученные выражения мы подставляем на место этих неизвестных в третье уравнение.

Возможны и иные планы. Поясним их на следующих примерах:

1. 3x – 4y + 3z = 19
4x – 6y + z = 22
7x – 18y = 33.

Мы видим, что в третье уравнение входят только 2 неизвестных, x и y. Поэтому постараемся получить из первых двух уравнений с тремя неизвестными новое уравнение с двумя неизвестными, а именно: также с x и y, — тогда мы будем иметь два уравнения с двумя неизвестными, которые умеем решать. Для этой цели исключим способом уравнивания коэффициентов из первых двух уравнений неизвестное z, для чего 1-ое уравнение оставим без изменения, а обе части второго умножим на –3. Получим:

3x – 4y + 3z = 19
–12x + 18y – 3z = –66.

Сложив по частям эти уравнения, получим:

Присоединим сюда еще третье из данных уравнений и решим их совместно способом уравнивания коэффициентов:

Подставляя это значение x – a в уравнение

Подставляя полученные для x и для y значения в простейшее из данных уравнений, а именно в уравнение

2. 3x + 5y – 9z = 29
5x + 2y – 6z = 17
4x – 10y + 3z = 17

Наметим следующий план: выберем сначала 2 из этих трех уравнений и из них способом уравнивания коэффициентов получим одно уравнение с двумя неизвестными; затем выберем вторую пару уравнений из данных и из них тем же способом получим второе уравнение с теми же двумя неизвестными. Применяясь к данным уравнениям, удобно будет выполнить этот план в следующем порядке: 1) возьмем 1-ое и 2-ое уравнение и из них, исключив способом уравнивания коэффициентов y, получим одно уравнение с x и z; 2) возьмем 1-ое и 3-е уравнения и из них также исключим y и получим второе уравнение с неизвестными x и z; 3) решим полученные 2 уравнения с неизвестными x и z также способом уравнения коэффициентов.

4) Подставим полученное для x значение в уравнение

–6 – 3z = 15 или 3z = –21 и z = –7.

Подставим полученные для x и z значения в уравнение

3. 4x – 2y + z = 4
5x + 3y – z = 11
3x + 7y – 2z = 7

Составим следующий план: 1) из первого уравнения определим z через x и y; 2) полученное выражение подставим на место z во 2-ое и в 3-е уравнения, – получим два уравнения с двумя неизвестными, а именно — с x и y; 3) решим полученные два уравнения.

2) 5x + 3y – (4 – 3x + 2y) = 11
3x + 7y – 2(4 – 3x + 2y) = 7

Упростим каждое из этих уравнений:

1-ое: 5x + 3y – 4 + 3x – 2y = 11 или 8x + y = 15.

2-ое: 3x + 7y – 8 + 6x – 4y = 7 или 9x + 3y = 15 или 3x + y = 5.

3) Вычтем по частям из 1-го уравнения второе:

8x + y = 15
3x + y = 5
–————
5x = 10, откуда x = 2.

4) Подставим полученное для x значение в уравнение

Подставим эти значения x – a и y – a в выражение для z: