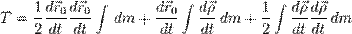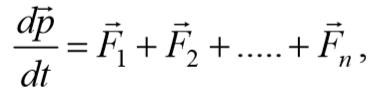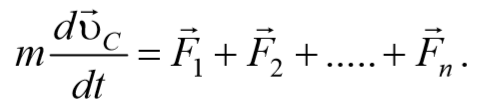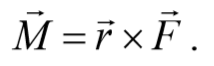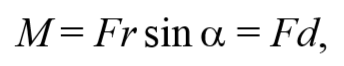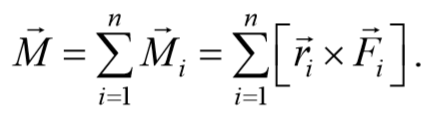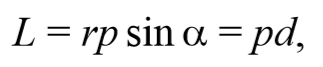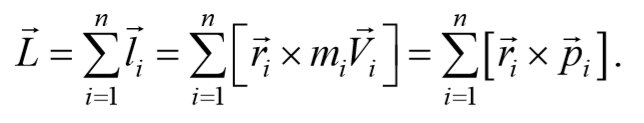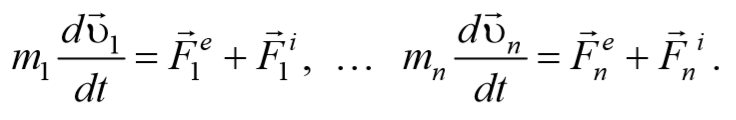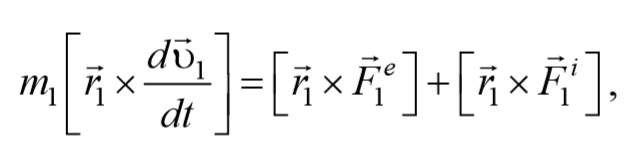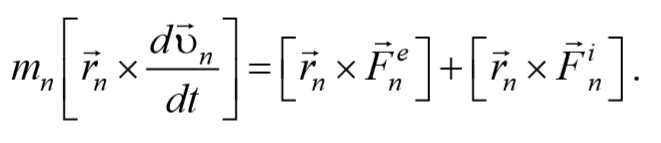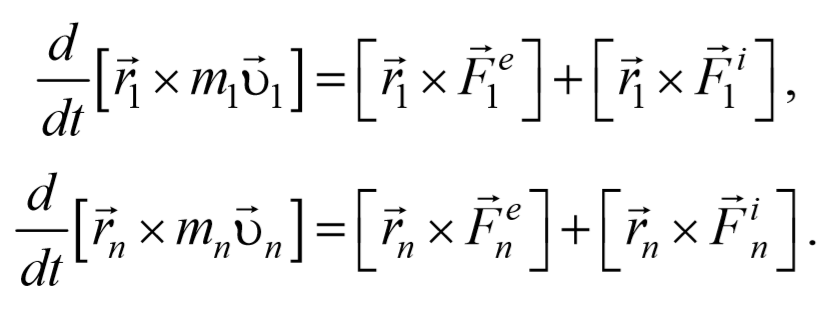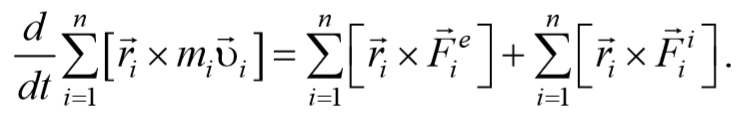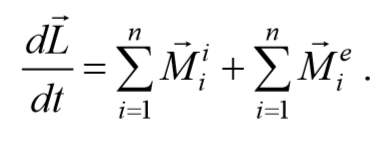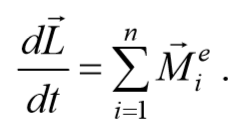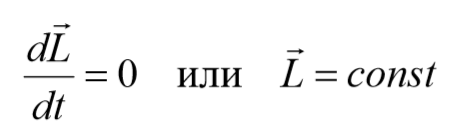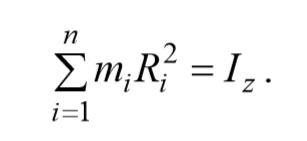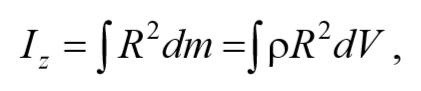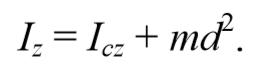Закон изменения момента импульса уравнение моментов

Закон изменения момента импульса.

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величинуL, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета. L = ΣL_i.

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы. dL/dt=M.

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее. В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.
Закон сохранения момента импульса.

Из закона изменения момента импульса, полученного нами для системы тел, вытекает закон сохранения момента импульса применительно к механике:

Момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Еще раз подчеркнем, что при использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.

Закон сохранения момента импульса является фундаментальным законом природы и выполняется для любых, а не только механических систем.

Следствия из закон сохранения момента импульса:

· в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;

· если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;

· в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Билет №14

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где , — расстояние от этой точки до оси вращения. Следовательно.

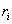
(5.11)

где — момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений — поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

(5.12)

где — момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.

Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где T — полная кинетическая энергия, — энергия движения центра масс, — относительная кинетическая энергия.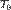

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.

Вывод

Выразим относительную кинетическую энергию T_r системы S как энергию, вычисленной относительно подвижной системы координат. Пусть — радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда:

Если — радиус-вектор начала координат подвижной системы, а — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:

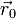
Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:

Раскрывая скобки и вынося из-под знака интеграла, получаем:

Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно, . Третий член равен T_r, введённой ранее относительной энергии системы.

Билет №15

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Основные понятия и постулаты СТО

Специальная теория относительности, как и любая другая физическая теория, может быть сформулирована на базе из основных понятий и постулатов (аксиом) плюс правила соответствия её физическим объектам.

Основные понятия

Система отсчёта представляет собой некоторое материальное тело, выбираемое в качестве начала этой системы, способ определения положения объектов относительно начала системы отсчёта и способ измерения времени. Обычно различают системы отсчёта и системы координат. Добавление процедуры измерения времени к системе координат «превращает» её в систему отсчёта.

Инерциальная система отсчёта (ИСО) — это такая система, относительно которой объект, не подверженный внешним воздействиям, движется равномерно и прямолинейно. Постулируется, что любая система отсчёта, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, также является ИСО.

Событием называется любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x, y, z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т. п.

Обычно рассматриваются две инерциальные системы S и S’. Время и координаты некоторого события, измеренные относительно системы S обозначаются как (t, x, y, z), а координаты и время этого же события, измеренные относительно системы S’, как (t’, x’, y’, z’). Удобно считать, что координатные оси систем параллельны друг другу и система S’ движется вдоль оси x системы S со скоростью v. Одной из задач СТО является поиск соотношений, связывающих (t’, x’, y’, z’) и (t, x, y, z), которые называются преобразованиями Лоренца.

Синхронизация времени

В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО. Пусть от первых часов, в момент времени t₁ ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью u. Сразу по достижении вторых часов (по их показаниям в момент времени T) сигнал отправляется обратно с той же постоянной скоростью u и достигает первых часов в момент времени t₂. Часы считаются синхронизированными, если выполняется соотношение T = (t₁ + t₂) / 2.

Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными.

В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.

Линейность преобразований

Простейшими преобразованиями между двумя ИСО являются линейные. Например, для координаты x и времени t можно записать:

где A_i,B_i,C_i — некоторые постоянные коэффициенты, которые могут зависеть от единственного параметра — относительной скорости v. Линейность преобразований обычно связывается с однородностью пространства и времени.

Вообще говоря, можно показать, что в общем случае преобразования между двумя ИСО должны быть дробно-линейными функциями координат и времени с одинаковым знаменателем [8] [9] . Для этого достаточно использовать определение ИСО: если некоторое тело имеет постоянную скорость относительно одной инерциальной системы отсчёта, то его скорость будет постоянна и относительно любой другой ИСО.

Для получения линейных преобразований необходимо выполнение более сильного требования: если два объекта имеют одинаковые скорости относительно одной инерциальной системы отсчёта, то их скорости будут равны и в любой другой инерциальной системе [10] .

[править] Согласование единиц измерения

Чтобы измерения, выполненные в различных ИСО, можно было между собой сравнивать, необходимо провести согласование единиц измерения между системами отсчёта. Так, единицы длины могут быть согласованы при помощи сравнения эталонов длины в перпендикулярном направлении к относительному движению инерциальных систем отсчёта. Например, это может быть кратчайшее расстояние между траекториями двух частиц, движущихся параллельно осям x и x’ и имеющих различные, но постоянные координаты (y, z) и (y’,z’). Поэтому при относительном движении систем вдоль оси x можно считать, что y’=y, z’=z.

Для согласования единиц измерения времени можно использовать идентично устроенные часы, например, атомные. Другой способ согласования единиц времени — это соглашение о некотором значении относительной скорости систем отсчёта. Если начало системы S’ (x’=0) движется со скоростью v вдоль оси x системы S, то его траектория в этой системе будет иметь вид x=vt. Аналогично, начало системы отсчёта S (x=0) движется относительно S’ со скоростью -v, поэтому имеет траекторию x’=-vt’. При этом событие совпадения начал отсчёта систем выбирается за начальный момент времени (t’=t=0, когда x’=x=0). Эти соглашения позволяют записать преобразования в следующем виде:

где коэффициенты γ(v), σ(v) зависят от относительной скорости систем отсчёта и для своего определения требуют дополнительных предположений.

Изотропность пространства

Пространство в инерциальных системах отсчёта предполагается изотропным (нет выделенных направлений). Это приводит к тому, что γ(v) является чётной функцией скорости: γ( − v) = γ(v).

Рассмотрим, например, измерение длины некоторого объекта (линейки), неподвижного в системе отсчёта S’. Если одновременно (Δt = 0) в системе S измерить координаты «начала» и «конца» линейки, то её длина Δx‘ = γ(v)Δx не должна зависеть от направления (знака) скорости v, откуда следует, что функция γ(v) является чётной.

Принцип относительности

Ключевым для аксиоматики специальной теории относительности является принцип относительности, утверждающий равноправие инерциальных систем отсчёта. Это означает, что все физические процессы в инерциальных системах отсчёта описываются одинаковым образом. Совместно с остальными постулатами, перечисленными выше, принципа относительности достаточно, чтобы получить явный вид преобразований координат и времени между ИСО.

Для этого необходимо рассмотреть три инерциальные системы S1, S2 и S3. Пусть скорость системы S2 относительно системы S1 равна v₁, скорость системы S3 относительно S2 равна v₂, а относительно S1, соответственно, v₃. Записывая последовательность преобразований (S2, S1), (S3, S2) и (S3, S1), можно получить следующее равенство:

Доказательство

Так как относительные скорости систем отсчёта v₁ и v₂ произвольные и независимые величины, то это равенство будет выполняться только в случае, когда отношение σ(v) / v равно некоторой константе α, единой для всех инерциальных систем отсчёта, и, следовательно, .

Существование обратного преобразования между ИСО, отличающегося от прямого только заменой знака относительной скорости, позволяет найти функцию .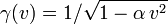

Доказательство

Таким образом, с точностью до произвольной константы α, получается явный вид преобразований между двумя ИСО. О численном значении константы α и её знаке без обращения к эксперименту ничего сказать нельзя. Если α > 0, то удобно ввести обозначение α = 1 / c 2 . Тогда преобразования принимают следующий вид:

и называются преобразованиями Лоренца. Из дальнейшего анализа станет ясно, что константа имеет смысл максимальной скорости движения любого объекта. Подобный вывод преобразований Лоренца стал известен спустя 5 лет после известной статьи Эйнштейна 1905 года, благодаря работам Игнатовского, Франка и Роте (см. исторический очерк).

Последнее изменение этой страницы: 2017-03-14; Просмотров: 2632; Нарушение авторского права страницы

Лекция №5. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА

4.1. Динамика поступательного движения твердого тела.

Движение любого твердого тела можно рассматривать как сумму поступательного движения его центра масс и вращательного движения относительно оси, проходящей через его центр масс.

Разобьем твердое тело на элементарные массы m_i , тогда его можно представить как систему материальных точек, взаимное расположение которых остается неизменным. Поэтому для описания поступательного движения тела можно использовать закон изменения импульса механической системы

p = $$<\sum_^n>$$ m_i υ _i=m υ _C — импульс всех материальных точек твердого тела.

Также можно воспользоваться понятием центра масс и к поступательному движению твердого тела применить закон движения центра масс

Центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, и на которую действуют все силы, приложенные к телу. Уравнение (4.1.2) дает возможность установить закон движение центра масс твердого тела, если известна масса тела и действующие на него силы. Если тело движется только поступательно, то это уравнение будет определять не только закон движения центра масс, но и любой другой точки тела.

4.2. Момент импульса. Момент силы.

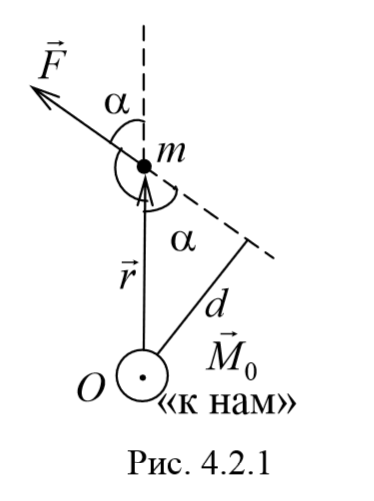
Момент силы. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенному из полюса в точку приложения силы, на силу F называется моментом силы материальнойточки относительно некоторого центра

Пусть на частицу массой m действует сила F , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент силы частицы относительно точки O дается уравнением (4.2.1). Направление момента силы M совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора r к силе F , и он перпендикулярен как вектору r , так и вектору F (рис. 4.2.1). Тогда модуль вектора момента силы равен

где d=r sin α − плечо силы относительно точки O .

Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.

Таким образом, модуль момента силы относительно оси, есть скалярная величина, характеризующая вращательное движение действия силы и равная произведению модуля силы F , действующей на твердое тело, на плечо силы d относительно этой оси.

Если на тело действует несколько сил, то суммарный момент этих сил равен векторной сумме моментов всех сил относительно данной оси:

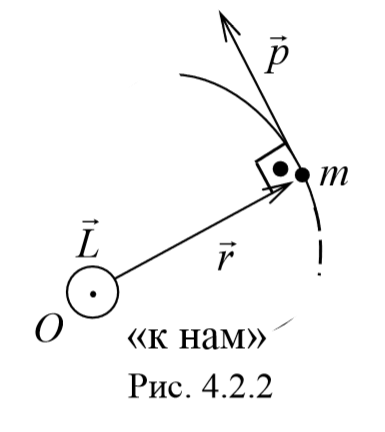
Момент импульса. Векторная величина, равная векторному произведению радиус-вектора r точки, проведенного из центра на ее импульс m υ называется моментом импульса материальной точки относительно некоторого центра

Пусть частица массой m имеет импульс p , а ее положение в некоторой инерциальной системе отсчета характеризуется радиус-вектором r относительно начала координат. Тогда момент импульса частицы относительно точки O дается уравнением (4.2.4). Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу p , и он перпендикулярен как вектору r , так и вектору p (рис. 4.2.2). Тогда модуль вектора момента импульса равен

где d − плечо импульса относительно точки O .

Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.

Таким образом, модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению импульса p на плечо импульса d относительно этой оси.

Моментом импульса механической системы относительно некоторого центра называется векторная величина, равная геометрической сумме моментов импульса относительно той же точки всех материальных точек системы

4.3. Основное уравнение динамики вращательного движения относительно точки.

Рассмотрим систему материальных точек массами m₁, m₂, . m_n движущихся со скоростями υ ₁, υ ₂, . υ _n . Пусть на каждую из этих точек действуют: равнодействующие внутренних сил F i ₁, F i ₂, . F i _n , и равнодействующие внешних сил F e ₁, F e ₂, . F e _n .

Запишем уравнения движения частиц:

Умножим каждое уравнение системы (4.3.3) на соответствующий радиус-вектор и получим

Преобразуем данные уравнения

Сложим эти уравнения и получим

В последнем уравнении:

Таким образом, выражение (4.3.6) можно записать в виде

Учитывая, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы всегда равна нулю, т. е. $$<\sum_^n>$$ M i _i=0 , получим основное уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы ).

4.4. Закон сохранения момента импульса.

Если момент внешних сил $$<\sum_^n>$$ M e _i=0 , то получим

закон сохранения момента импульса.

Если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы относительно этого центра с течением времени не изменяется.

Можно сказать, что момент силы при вращательном движении является аналогом силы при поступательном движении, момент импульса − аналогом импульса.

Законы изменения и сохранения момента импульса механической системы можно применить и к вращательному движению твердого тела.

4.5. Момент инерции.

Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:

Момент инерции зависит только от формы тела и расположения масс относительно оси. [I]=1 кг · м 2 .

Понятие момента инерции было введено при рассмотрении вращения твердого тела. Однако следует иметь в виду, что каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Если тело сплошное, то суммирование в выражении (4.5.1) следует заменить на интегрирование:

где R − расстояние от элементарной массы dm до оси вращения.

4.6. Теорема Штейнера. Правило аддитивности

Существуют два свойства момента инерции:

1) Теорема Штейнера: момент инерции тела I_z относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:

2) Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:

Понятие о моменте импульса, его закон сохранения и пример решения задачи

Вращательное движение является не менее распространенным в природе, чем линейное перемещение объектов. Чтобы убедиться в этом, достаточно вспомнить вращение колес автомобилей и велосипедов, лопастей вертолетов и вентиляторов, планет вокруг своей оси и вокруг своих звезд. Для описания процесса кругового перемещения объектов используется физическая величина, которая получила название «момент импульса». Рассмотрим в статье, что она собой представляет.

Момент импульса частицы и ось вращения

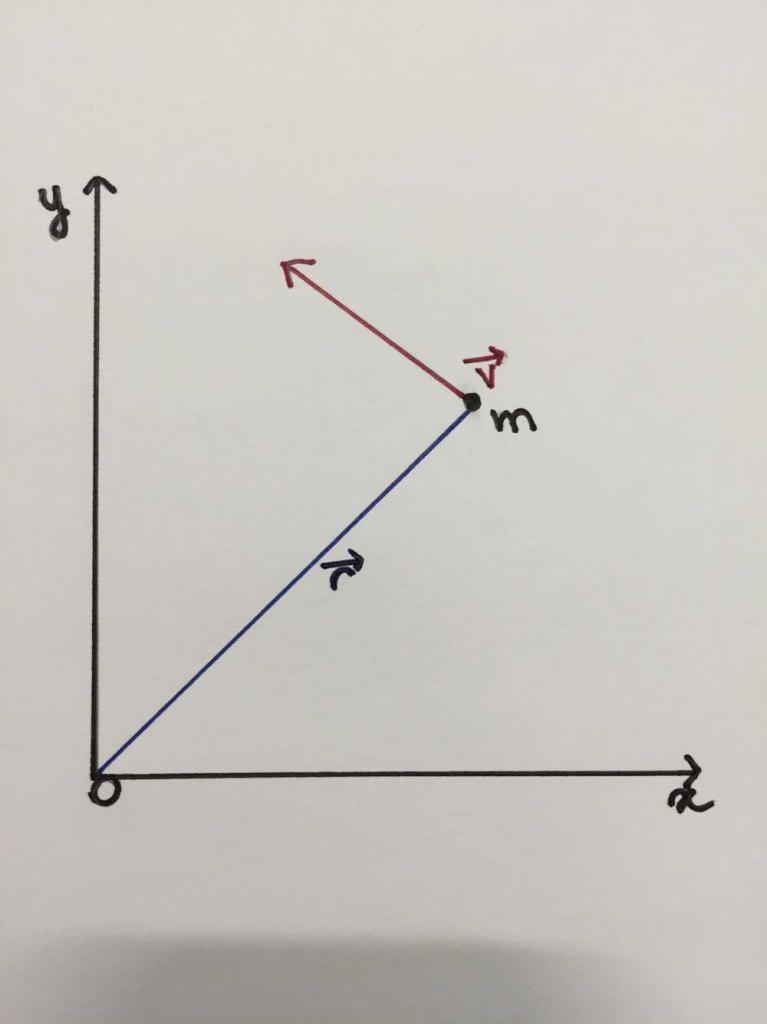
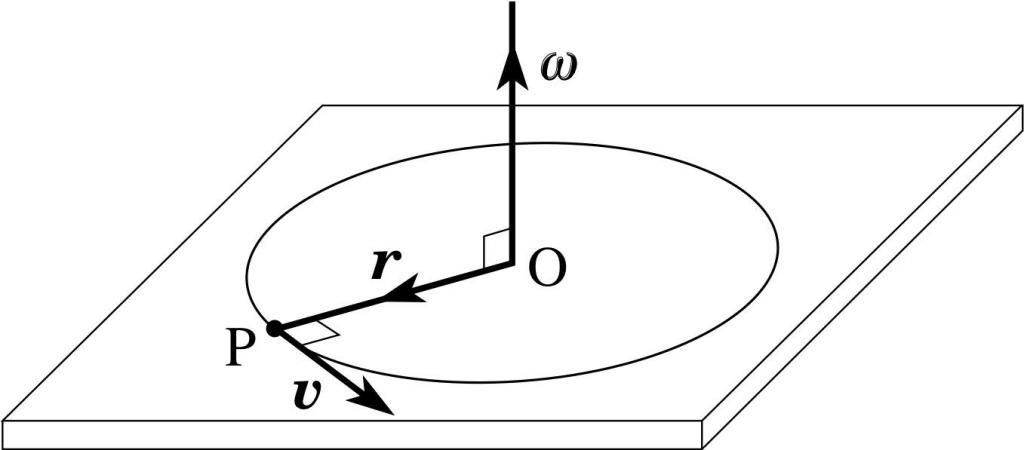
Ниже приведен рисунок, на котором схематически показано, что некоторая частица или материальная точка массой m совершает движение по круговой траектории радиусом r¯ со скоростью v¯, направленной по касательной. Ось вращения расположена перпендикулярно плоскости рисунка в точке O.

Введем следующую физическую величину:

Она называется моментом импульса, или угловым моментом. Как видно, это векторная величина. Ее направление можно определить по правилу правой руки: необходимо направить 4 пальца таким образом, чтобы они, двигаясь вдоль вектора r¯, приходили к концу вектора p¯ (или v¯), тогда большой палец покажет направление L¯. В рассматриваемом случае L¯ направлен к читателю перпендикулярно плоскости рисунка.

Поскольку на рисунке скорость (импульс) частицы направлена под прямым углом к вектору r¯, то приведенное уравнение можно переписать в скалярной форме:

Угловая скорость и момент инерции

Момент импульса частицы из предыдущего примера можно записать через угловую скорость ω. Для этого воспользуемся ее связью со скоростью линейной:

Подставляя последнее равенство в скалярное уравнение для L, получим:

Здесь I — это момент инерции частицы. Полученное выражение используется часто для решения практических задач, одна из которых будет рассмотрена ниже.

Закон сохранения вращательного движения

Движение по кругу так же, как и линейное перемещение объектов в пространстве, характеризуется законами сохранения. Одним из них является сохранение момента импульса. Получим этот закон.

Уравнение рассматриваемого типа движения имеет следующий вид:

Где dL/dt характеризует изменение момента импульса тела во времени, когда на него оказывает действие некоторый момент M, создаваемый внешними (не внутренними) силами. Если этот момент сил равен нулю, тогда зануляется и левая часть выражения, что означает L=const. Для этого случая можно записать такое равенство:

Что означает эта запись? Она говорит о том, что если некоторое тело вращалось со скоростью ω₁ и имело момент инерции I₁, затем по причине каких-либо внутренних (не внешних) сил изменился момент инерции и стал равным I₂, то новая скорость вращения ω₂ будет пропорционально связана с этим изменением.

Записанное соотношение называется законом сохранения момента импульса точки (тела) по аналогии с соответствующим законом для линейных величин (сохранение импульса), поскольку роль массы играет момент инерции I, а скорости — угловая величина ω.

Использование закона L = const

Рассмотренное в предыдущем пункте соотношение можно видеть в действии, когда выступают фигуристы или балерины. Они, выполняя сложные акробатические номера, раскручивают свое тело, разбрасывая при этом руки и ноги, а затем прижимают конечности к телу. Последнее действие приводит к уменьшению величины I и, соответственно, к увеличению скорости вращения, что создает достаточно зрелищный эффект.

Другим примером использования неизменности момента импульса системы является реализация поворота искусственного спутника в космическом пространстве. Для этого запускают специальный прикрепленный к нему маховик. Поскольку общий угловой момент не должен измениться за счет действия внутренних сил, то сам спутник начинает вращаться в противоположном направлении. Как только он повернется на нужный угол вокруг своей оси, маховик останавливают с помощью электромотора, и корпус спутника также прекращает свое вращение.

Вычисление момента инерции

Поскольку в законе сохранения кругового движения присутствует величина I, то следует сказать несколько слов про нее. Она характеризует инерционность системы, то есть насколько «трудно» или «легко» ее раскрутить. Например, маховик автомобиля обладает большой массой и относительно большим радиусом, поэтому его момент инерции является значительным. Наоборот, колесо велосипеда сделано из алюминиевого легкого обода, поэтому для него I будет сравнительно небольшим.

Для вычисления этой физической характеристики следует использовать формулу:

Откуда видно, что момент инерции — это характеристика системы, в которую входит тело вращения, а не самого тела. Этот факт отличает I от линейной инерции, которая зависит исключительно от свойств тела (его массы).

Задача с вращающимся стержнем

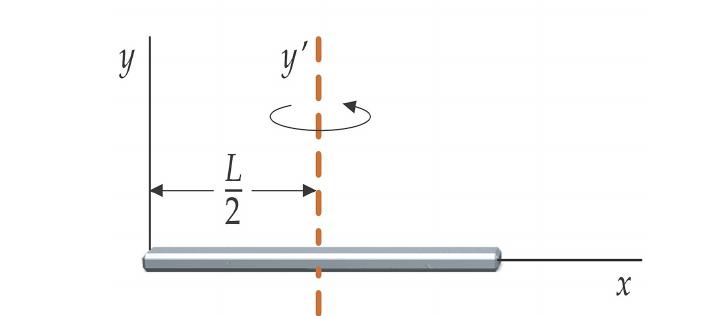
Решим интересную задачу: имеется твердый стержень, который вращается вокруг оси, расположенной на его конце. Если плавно сместить эту ось в центр массы стержня, как изменится его скорость вращения?

Это классическая задача на применение закона сохранения момента импульса. Трудность заключается в вычислении изменения момента инерции. Для этого можно самостоятельно воспользоваться приведенной выше формулой с интегралом, но проще будет посмотреть необходимые значения I в справочной литературе.

В начале ось вращения проходила через конец стержня. Для этой системы момент инерции равен:

I₁ = m*L 2 /3, где L — длина стержня, m — его масса.

Когда ось сместили в центр массы объекта, то изменился его момент инерции, он стал равен:

Применяем закон сохранения для L, получаем:

Мы получили ответ на задачу: стержень станет вращаться в 4 раза быстрее, чем вначале.