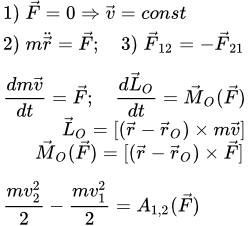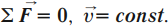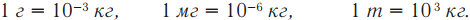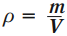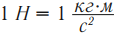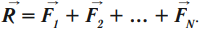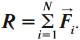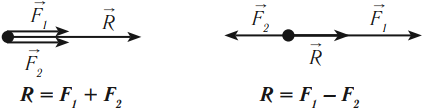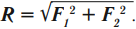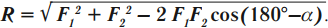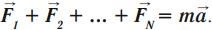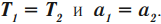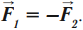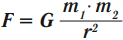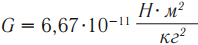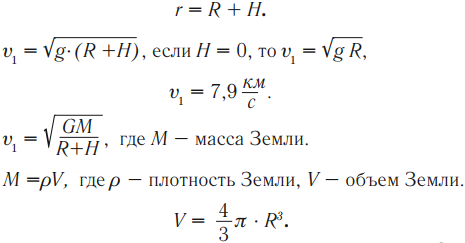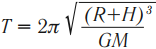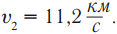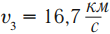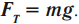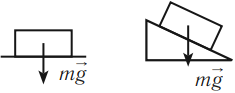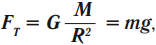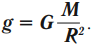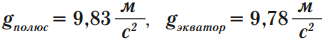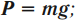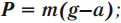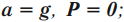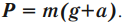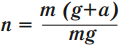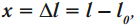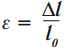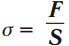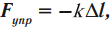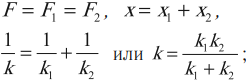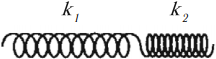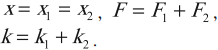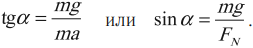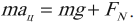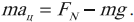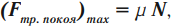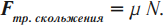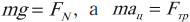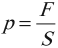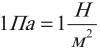Законы динамики и уравнения движения точки

Динамика материальной точки. Все законы и теоремы

Законы динамики

Первый закон Ньютона (закон инерции Галилея)
Существуют такие системы отсчета, относительно которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если точка покоилось в определенный момент времени, то она будет покоиться и в последующие моменты.

Не во всех системах отсчета выполняется закон инерции. Например, если мы выберем систему отсчета, связанную с ускоряющейся ракетой, то относительно этой системы, не взаимодействующие материальные точки, не будут двигаться прямолинейно и равномерно.

Инерциальная система отсчета – это система отсчета, в которой справедлив закон инерции.
Движение по инерции – это движение точки, совершаемое при отсутствии действующих на нее сил.

Второй закон Ньютона (основной закон динамики)
Взаимодействие на выбранную материальную точку со стороны других тел описывается вектором, который называется силой. При этом, в инерциальных системах отсчета, действие силы приводит к ускорению точки , которое пропорционально приложенной силе, имеет одинаковое с ней направление, и обратно пропорционально массе точки:
(1) .

Если есть радиус-вектор, проведенный из начала координат к точке, то ускорение есть вторая производная радиус-вектора по времени:
.
Производную по времени, в теоретической механике, обозначают точкой над переменной, а не штрихом, как в математическом анализе.

Если на точку действует не одна, а n сил, то в правой части производится суммирование по всем силам, действующих на точку. Тогда уравнение (1) примет вид:
(2) .

Третий закон динамики (закон равенства действия и противодействия)
Если две материальные точки действуют друг на друга, то сила, с которой первая точка действует на вторую, равна по абсолютной величине и противоположна по направлению силе, с которой вторая точка действует на первую. При этом силы направлены вдоль прямой, соединяющей точки.

Закон независимости сил
Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.

То есть уравнение (2) можно записать в виде:
, где .

Задачи динамики

Первая задача динамики
Зная закон движения точки, определить действующую на нее силу.

Вторая (основная) задача динамики
Зная действующие на точку силы, определить ее закон движения.

Основные виды сил

Единицей измерения силы в СИ является 1 ньютон (1 Н = кг·м/с 2 ). Это сила, которую нужно приложить к точке массой 1 кг, чтобы она получила ускорение 1 м/с 2 .

Сила тяжести.
Сила тяжести действует на любую материальную точку, находящуюся на поверхности Земли. Она пропорциональна массе точки и равна
,
где – ускорение свободного падения, направленное вниз. Его величина зависит от широты и высоты над уровнем моря. Стандартное значение, принятое при построении систем единиц, составляет м/с 2 .

Сила тяготения.
.
Здесь – массы точек, r – расстояние между ними, Н·м 2 /кг 2 – гравитационная постоянная.

Для точки массы m на поверхности Земли имеем: . Отсюда . Тогда силу тяготения Земли можно вычислять по формуле:
,
где R = 6371 км – радиус Земли; r – расстояние от точки до центра Земли.

Сила электростатического взаимодействия.
,
где – величины зарядов; r – расстояние между ними; Н·м 2 /Кл 2 – коэффициент. Одноименные заряды отталкиваются, разноименные – притягиваются.

Сила трения скольжения
возникает при скольжении одного тела по поверхности другого. Она направлена в сторону, противоположную скорости движения. Ее величина определяется по формуле:
F = fN ,
где N – сила давления, перпендикулярная поверхности, с которой скользящее тело прижимается к поверхности; f – коэффициент трения, который зависит от материалов соприкасаемых тел.

Сила упругости.
Эта сила возникает при деформации упругих тел. Это могут быть растяжения, сжатия и изгибы. Она определяется по формуле
F = cλ ,
где λ – величина деформации; c – коэффициент, который зависит от материала упругого тела. Для пружины λ – это удлинение или сжатие пружины; c – коэффициент жесткости.

Сила вязкого трения.
При движении тела в вязкой среде с небольшими скоростями, на него действует сила трения, пропорциональная скорости движения:
F = μv ,
где v – скорость тела; μ – коэффициент сопротивления.
При больших скоростях, сила трения пропорциональна квадрату скорости.

Дифференциальные уравнения движения точки

Спроектируем уравнение (2) на оси прямоугольной системы координат. Пусть радиус вектор точки имеет в этой системе компоненты (проекции) . Тогда из векторного уравнения (2) получаем систему уравнений:
.
Это есть дифференциальные уравнения движения точки в прямоугольной системе координат.

Спроектируем уравнение (2) на оси естественного трехгранника:
.
Здесь – единичный вектор, направленный по касательной к траектории; – единичный вектор, перпендикулярный и лежащий в касательной плоскости траектории; – единичный вектор, перпендикулярный и . Поскольку , то .
Вводим пройденный путь s , измеренный вдоль дуги траектории точки. Пусть ρ – радиус кривизны траектории в рассматриваемой точке. Тогда, для естественного способа задания движения точки, уравнения движения примут вид:
.

Уравнения движения в полярных координатах для плоского движения:
.

Прямолинейное движение точки

Пусть ось x направлена вдоль линии движения точки. Тогда уравнение движения имеет вид:
(3) .
Его общее решение:
,
где – произвольные постоянные. Их находят из начальных условий:
.

Если сила F_x зависит только от времени, то из уравнения (3) сначала определяют скорость v_x , а затем координату x , последовательно интегрируя уравнения:
.
Если сила зависит только от координаты x , то выполняют преобразование:
;
;
.

Колебательное движение материальной точки

Свободные колебания

Рассмотрим движение груза на пружинке. Считаем, что груз является материальной точкой; массой пружины можно пренебречь; и отсутствует сила тяжести. Пусть движение происходит вдоль оси x . За начало отсчета выберем такое положение груза, при котором пружина не деформирована. Тогда на точку действует только восстанавливающая сила упругости пружины, которая определяется по закону Гука:
(К1) ,
где x – деформация пружины; c – коэффициент жесткости. Он равен силе, которая возникает при деформации, равной единице (один метр) и имеет размерность [Н/м]. Из (К1) видно, что сила является восстанавливающей, то есть направлена так, чтобы вернуть точку в начало координат к недеформированному состоянию. Сила такого вида возникает не только при деформации пружины, но и во многих других случаях при небольшом отклонении точки от равновесного положения.

Составим уравнение движения точки и выполняем преобразования:
.
Введем обозначение . В результате получаем.

(К2) .
Уравнение (К2) называется дифференциальным уравнением свободных колебаний. Его также называют дифференциальным уравнением гармонических колебаний. Оно является линейным однородным дифференциальным уравнением второго порядка.

Ищем его решение в виде . Получаем характеристическое уравнение:
.
Оно имеет два мнимых корня: . Тогда общее решение уравнения (К2) имеет вид:
,
где и – произвольные постоянные. Они определяются из начальных условий. Пусть – координата и скорость точки в начальный момент времени , тогда
;
.

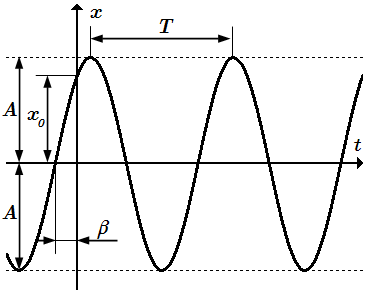
График гармонического движения точки.

Часто бывает удобно вместо постоянных интегрирования и перейти к новым постоянным A и β по формулам: . Тогда
(К3) .
Это есть уравнение гармонического колебательного движения точки. Здесь – амплитуда колебаний;
– фаза колебаний;
β – начальная фаза, ;
– циклическая частота колебаний, которую также называют угловой или собственной.
Период колебаний: .
Частота колебаний: – это число циклов колебаний, совершенных в единицу времени. Она широко применяется в технике, однако для математического описания более удобна угловая частота, которую мы будем использовать в дальнейшем и называть просто частотой.

Частота k и период T не зависят от начальных условий, а амплитуда и фаза – зависят. Кроме этого, k и T не зависят от амплитуды. Колебания, у которых частота и период не зависят от амплитуды, называют изохорными колебаниями. Если рассмотреть колебания с большой амплитудой, при которой закон Гука (К1) не выполняется, то уравнение (К2) не будет линейным и колебания не будут изохорными.

Влияние постоянной силы

Пусть теперь, наряду с восстанавливающей силой (К1), на точку действует постоянная сила P , например сила тяжести. Тогда уравнение движения примет вид:
.
Это приводит к смещению центра колебаний в сторону действия силы P на величину
δ _ст = P/c .
Это смещение называют статическим отклонением. Если P – сила тяжести, то
.

Колебания при вязком трении

Пусть на точку, кроме силы упругости пружины, действует сила сопротивления среды. При малых скоростях она пропорциональна скорости точки:
. Это так называемое вязкое трение. Составим уравнение движения:
. Обозначив μ/m= 2 b , получаем:
(К4) . Составляем характеристическое уравнение:
(К5) . Оно имеет два корня:
.

Затухающие колебания

При b , корни характеристического уравнения (К5) комплексные:
. Тогда общее решение уравнения (К4) имеет вид:
,
где . Обозначим , . Тогда
(К6) .
, ;
– амплитуда (переменная величина);
b – коэффициент затухания;
– частота затухающих колебаний;
– период затухающих колебаний. Он больше периода свободных колебаний. При небольшом коэффициенте затухания (при b/k ≪ 1 ) T ₁ ≈ T .
Колебания, происходящие по закону (К6) называются затухающими. График затухающих колебаний заключен между двумя кривыми x = ±Ae –bt , симметричными относительно оси t .

Затухающие колебания можно рассматривать как гармонические колебания с переменной амплитудой . Относительное изменение переменной амплитуды за период колебания называется декрементом колебаний. Он равен
. Модуль логарифма декремента называется логарифмическим декрементом. Он равен .

Апериодическое движение точки

При (или ) корни характеристического уравнения (К5) действительные. Поэтому движение точки является апериодическим.
При (или ) характеристическое уравнение (К5) имеет два различных действительных корня:
. Тогда общее решение уравнения (К4) имеет вид:
(К7) .
Сюда не входят тригонометрические функции. Поэтому это апериодическое движение. Точка может пройти через положение равновесия x = 0 не более одного раза.

Закон движения (К7) можно выразить через гиперболические функции, если положить: . Тогда
.
Перейдем к новым постоянным интегрирования A и β , выполнив подстановку:
. Тогда
.

При b = k характеристическое уравнение (К5) имеет два кратных вещественных корня . Общее решение уравнения (К4) имеет вид:
.
Движение также апериодическое. Точка может пройти через положение равновесия x = 0 не более одного раза.

Вынужденные колебания

Рассмотрим случай, когда кроме восстанавливающей силы , на точку действует возмущающая сила, меняющаяся по гармоническому закону:
(К8) . Составим уравнение движения:
.
Введем обозначение h=H/m . Разделив на m , получаем дифференциальное уравнение вынужденных колебаний:
(К9) .

Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами со специальной неоднородной частью. Его общее решение равно сумме общего решения однородного уравнения и частного (то есть любого, отличного от нулевого) решения данного уравнения:
;
;
.
Общее решение однородного уравнения: .
Ищем частное решение в виде . В результате получаем:
;
.

Коэффициент динамичности. Действие постоянной возмущающей силы величины H приводит к статическому отклонению . Периодическая возмущающая сила (К8) с амплитудой H приводит к периодическим колебаниям с амплитудой . В связи с этим вводят коэффициент динамичности: .
Он показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение.

Явление резонанса и биения

Когда частота возмущающей силы равна частоте собственных колебаний p = k , коэффициент динамичности стремится к бесконечности, амплитуда колебаний неограниченно возрастает. Это явление называется резонансом. Уравнение движения точки при p = k имеет вид:
(К10) .
Оно имеет частное решение
.
Общее решение уравнения (К10):
.
Это уравнение показывает, что амплитуда вынужденных колебаний возрастает пропорционально времени. Фаза вынужденных колебаний отстает от фазы возмущающей силы на π/ 2 .

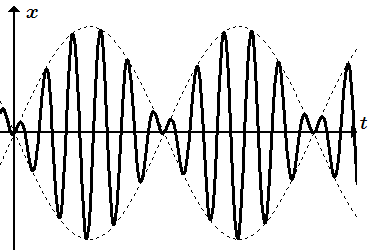
Биения.

Когда частота p возмущающей силы близка к собственной частоте k колебания точки, p/k ≈ 1 , возникает явление, называемое биениями. В этом случае частное решение уравнения (К9) имеет вид:
,
где .
Происходит наложение колебаний. Их можно рассматривать как вынужденные колебания частоты с переменной амплитудой, которая является периодической функцией с частотой .

Вынужденные колебания при наличии вязкого трения

Составим уравнение движения вынужденных колебаний при наличии вязкого трения:
.
Получаем дифференциальное уравнение:
.
Его общее решение имеет вид.
1) при b :
;
2) при b > k :
;
3) при b = k :
.
Здесь ;
ε определяется из уравнений:
.
Величины A и β являются постоянными интегрирования. Они определяются из начальных условий.

Общие теоремы динамики точки

Теорема об изменении количества движения материальной точки

Теорема об изменении количества движения материальной точки в дифференциальной форме
Изменение количества движения материальной точки за бесконечно малый промежуток времени dt равно элементарному импульсу равнодействующей сил, приложенных к этой точке:
.
Эту теорему можно сформулировать так:
Производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке:
(Т1) .

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если проинтегрировать уравнение (Т1) по времени от начального момента времени t = 0 до конечного момента t = t₁ , то получим теорему в интегральной форме.

Теорема об изменении количества движения материальной точки в интегральной форме
изменение количества движения материальной точки за конечный промежуток времени [0,t₁] равно импульсу силы, приложенной к этой точке, за тот же промежуток времени:
.
Здесь – скорость точки в моменты времени t = 0 и t = t ₁ , соответственно.

Теорема об изменении момента количества движения материальной точки

Теорема об изменении момента количества движения материальной точки
Производная по времени от момента количества движения материальной точки, относительно произвольного центра O , равна моменту равнодействующей силы, приложенной к точке, относительно того же центра:
.

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если на точку действует несколько сил , то равнодействующая сила равна их геометрической сумме:
.
Тогда можно записать эту теорему так:
.

Далее будем считать, что точка O выбрана в начале координат. Тогда .

Центральная сила. Второй закон Кеплера

Пусть на точку действует центральная сила с центром в начале координат O . Тогда ее момент относительно O равен нулю. По теореме об изменении момента количества движения материальной точки имеем:
.
Если ввести секторную скорость , то она оказывается постоянной
.
Получаем второй закон Кеплера (закон площадей).

Второй закон Кеплера (закон площадей)
Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью. То есть радиус-вектор точки заметает равные площади в любые равные промежутки времени.

Работа силы. Мощность

Основные понятия

Единицей измерения работы в СИ является 1 джоуль (1 Дж = 1 Н·м = кг·м 2 /с 2 ).

Работа силы при движении материальной точки от точки M ₁ до точки M ₂ равна сумме (интегралу) элементарных работ:
.
Если ввести скорость точки , то
.

Теорема о работе силы
Работа A равнодействующей силы на некотором перемещении равна алгебраической сумме работ A_k составляющих сил на том же перемещении:
.

Мощность – это величина работы, произведенная за единицу времени.
.

Единицей измерения мощности в СИ является 1 ватт (1 Вт = 1 Дж/с). Другие единицы мощности: 1 кВт (киловатт) = 1000 Вт; 1л.с.(лошадиная сила) = 736 Вт = 75 кгс·м/с.

Работа основных видов сил

Работа силы тяжести:
,
где P – сила тяжести, действующая на точку. Если начальная точка выше конечной, то работа положительна; если начальная точка ниже конечной, то отрицательна.

Работа силы упругости:
.
Здесь – деформация пружины в начальном положении; – в конечном.

Работа силы трения. Если сила трения постоянна, то
,
где s – длина пройденного точкой пути; – сила трения, которая всегда направлена в сторону, противоположную перемещению; f – коэффициент трения; N – нормальная реакция поверхности. Работа силы трения всегда отрицательна.

Работа силы тяготения.
На точку, находящуюся вблизи планеты Земля, на расстоянии r ≥ R от ее центра, действует сила притяжения
,
где R = 6371 км – радиус Земли. Тогда при перемещении точки из положения M₁ в положение M₂, сила тяготения совершит работу
.
Она не зависит от траектории движения тела.

Теорема об изменении кинетической энергии точки

Теорема об изменении кинетической энергии точки в дифференциальной форме
Дифференциал кинетической энергии точки равен сумма элементарных работ всех действующих на точку сил:
.

Проинтегрировав обе части этого уравнения вдоль траектории движения точки от положения M₁ до M₂, получим теорему в интегральной форме.

Теорема об изменении кинетической энергии точки
Изменение кинетической энергии материальной точки, при переходе ее из начального положения M₁ в конечное положение M₂, равно сумме работ всех сил, приложенных к точке на этом перемещении:
.

Силовые поля и потенциальная энергия

1. Работа сил стационарного поля при перемещении точки из положения M₁ в положение M₂ зависит только от начального положения M₁, конечного положения M₂, и формы траектории, но не зависит от закона движения точки.

2. Работа, совершенная полем при перемещении точки из положения M₁ в M₂ равна по модулю и обратна по величине работе, совершенной полем при перемещении точки из M₂ в M₁ при перемещении по той же траектории:
.

Для нестационарных полей эти свойства на выполняются.
Примеры стационарных полей: поле силы тяжести на поверхности Земли; электростатическое поле от неподвижно закрепленного заряда; поле силы упругости пружины, один конец которой закреплен.

Потенциальное силовое поле – это стационарное силовое поле, работа сил которого зависит только от начального M₁ и конечного M₂ положений точки, и не зависит от формы ее траектории. Потенциальное силовое поле также называют консервативным.

В потенциальном поле существует такая функция, через которую можно выразить вектор силы , действующей на точку.

Силовая функция – это функция, зависящая от координат точки ( x, y, z ) , через которую выражаются проекции силы потенциального поля на оси координат:
.

Отсюда следует, что сила не изменится, если к силовой функции прибавить постоянную. Таким образом, силовая функция определена с точностью до произвольной постоянной.

В потенциальном поле элементарная работа является дифференциалом от силовой функции:
.
Работа при конечном перемещении из точки в точку равна разности силовой функции в этих точках:
.
Таким образом, в потенциальном поле, работа сил поля не зависит от формы траектории. На замкнутом перемещении работа равна 0. Для более наглядной физической интерпретации, вводят понятие потенциальной энергии. Она равна, с точностью до произвольной постоянной, силовой функции, взятой с обратным знаком.

Потенциальная энергия П – это работа, которую нужно совершить при перемещении точки в потенциальном поле из данного положения в произвольным образом выбранное нулевое положение.

Так, для поля деформации, в качестве нулевого положения обычно принимают не деформированное положение; для гравитационного и электростатических полей за нулевое выбирают положение, бесконечно удаленное от тела или заряда. Для силы тяжести в поле Земли принимают любое, удобное для расчета положение. Таким образом, потенциальная энергия равна силовой функции, взятой с обратным знаком плюс постоянная, зависящая от выбора нулевого положения:
.

Пусть – нулевое положение. Тогда
;
.

Работа сил поля при перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий: .

Эквипотенциальные поверхности – это поверхности равного потенциала:
.

Сила направлена перпендикулярно эквипотенциальной поверхности.

Закон сохранения механической энергии
Если точка находится в потенциальном поле, то сумма ее кинетической и потенциальной энергий является постоянной:
.
Если на точку действуют несколько сил от разных потенциальных полей, то в качестве потенциальной энергии нужно взять сумму потенциальных энергий от каждого силового поля:
.

Основные виды потенциальных полей

В поле силы тяжести, потенциальная энергия зависит от высоты. Направив ось z вертикально вверх, получим: .

Поле силы упругости пружины. В этом поле, потенциальная энергия зависит от деформации λ пружины:
.
В качестве нулевого положения выбирают положение без деформации: λ = 0 .

Сила гравитационного притяжения и космические скорости

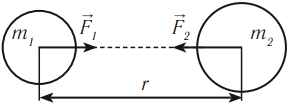
Между любыми двумя точками массами m ₁ и m ₂ , действует сила всемирного тяготения. Так, на точку 2 действует сила притяжения со стороны точки 1:
,
направленная вдоль прямой, проходящей через точку 1. Здесь r – расстояние между точками; Н·м 2 /кг 2 – гравитационная постоянная.

В результате притяжения, обе точки получают ускорения и движутся друг относительно друга. Мы рассмотрим более простой, но важный случай, когда масса M = m ₁ одного из тел намного больше массы m = m ₂ второго тела. Тогда точка с меньшей массой практически не оказывает влияния на движение более массивной точки. Выберем начало инерциальной системы координат в точке 1. Тогда силу гравитационного притяжения можно рассматривать как центральную силу и представить ее в векторном виде:
(П1) .
Потенциальная энергия точки 2:
(П2) .
Здесь нулевое положение выбрано на бесконечности: .

Формулы (П1) и (П2) справедливы, если объект 1 является шаром с плотностью, зависящей только от расстояния r до его центра. Пусть R – радиус такого шара. Тогда в формулах (П1) и (П2) r – это расстояние от центра шара 1 до точки 2. Они справедливы при .

Эти формулы можно использовать при расчете движения спутников вокруг Земли. Поскольку Земля вращается вокруг своей оси, то ее форма является эллипсоидом. Но в первом приближении Землю можно считать шаром радиуса R = 6371 км. Из таких допущений можно оценить космические скорости, необходимые для выведения летательных аппаратов на космические орбиты.

Первая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на круговую орбиту. Она равна км/с. Если у тела первая космическая скорость, то оно может вращаться по круговой орбите, не падая на Землю, то есть стать ее спутником.
Вторая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на параболическую орбиту. Она равна км/с. Если у тела скорость больше второй космической, то ее траекторией является гипербола, и, при отсутствии помех, оно будет удаляться от Земли и никогда не вернется назад.

Однако Солнце является той преградой, которая не даст спутнику со второй космической скоростью удалиться на бесконечное расстояние. Чтобы тело могло покинуть пределы солнечной системы, ему необходимо сообщить третью космическую скорость км/с.

Использованная литература:
А. А. Яблонский, Курс теоретической механики, часть II, динамика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 11-12-2019

Динамика

Динамика – это раздел механики, который рассматривает законы движения тел и те причины, которые его вызывают или изменяют.

Инерция – это свойство тела сохранять состояние покоя или прямолинейного и равномерного движения при отсутствии воздействия на него других тел или их компенсации.

Инерциальные системы отсчета. Первый закон Ньютона

Инерциальные системы отсчета – это системы отсчета, относительно которых тела движутся с постоянной по модулю скоростью в отсутствие или при компенсации внешних воздействий.

Инерциальной системой отсчета является система отсчета, связанная с Землей.

Первый закон Ньютона
Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или их действие компенсируется:

Физический смысл закона:

• из всех систем отсчета первый закон выделяет только инерциальные системы отсчета;
• закон утверждает, что будет происходить с телом, если на него не действуют другие тела или действие других тел скомпенсировано.

Согласно первому закону Ньютона, когда силы, действующие на движущееся тело, уравновесят друг друга, оно станет двигаться прямолинейно и равномерно, а если оно ранее покоилось, то и останется в покое.

Следствие
Если существует хотя бы одна инерциальная система отсчета, то существует и бесконечное множество таких систем.

Важно!
Скорость движения тела постоянна, если на него не действуют другие тела или действие других тел компенсируется.

Принцип относительности Галилея

Принцип относительности Галилея
Все законы механики имеют одинаковый вид во всех инерциальных системах отсчета.

Никакими механическими опытами нельзя отличить одну инерциальную систему отсчета от другой.
Связь координат точки в системах отсчета, движущихся друг относительно друга, описывается преобразованиями Галилея. Преобразования всех других кинематических величин являются их следствиями.

Важно!
Преобразования Галилея вместе с утверждением о независимости течения времени от движения отражают суть классических представлений о пространстве – времени. Согласно этим представлениям расстояния между телами одинаковы во всех системах отсчета и течение времени одинаково во всех инерциальных системах отсчета.

Масса тела. Плотность вещества

Причиной изменения скорости движения тела является его взаимодействие с другими телами. Все тела обладают свойством, которое называется инертностью.
Инертность – это способность тела изменять свою скорость не мгновенно, а за определенный промежуток времени.

Масса – это скалярная физическая величина, являющаяся мерой инертности тела.

Чем больше масса тела, тем труднее изменить его скорость и тем сильнее оно притягивает другие тела.
Свойства массы:

• масса не зависит от того, движется тело или покоится;
• масса тела равна сумме масс его частей.

Обозначение – ​ \( m \) ​, единицы измерения – кг (г, мг, т).

Плотность тела – это скалярная физическая величина, равная отношению массы тела к его объему.

Обозначение – ​ \( \rho \) ​, единицы измерения – кг/м 3 .

Сила – это векторная физическая величина, которая является количественной мерой взаимодействия тел, в результате которого они изменяют свою скорость или деформируются.

Обозначение – ​ \( F \) ​, единицы измерения – Н (Ньютон).

1 Ньютон равен силе, которая телу массой 1 кг сообщает ускорение 1 м/с 2 :

Существуют четыре вида сил различной природы:

• электромагнитные силы – силы, действующие между телами вследствие того, что тела состоят из движущихся заряженных частиц, между которыми действуют электрические и магнитные силы (сила трения, сила упругости);
• гравитационные силы – это силы притяжения одних тел к другим вследствие наличия у них массы (сила тяжести, сила тяготения);
• ядерные силы – это силы, действующие между протонами и нейтронами внутри атомов;
• слабые силы – это силы, удерживающие элементарные частицы от распада.

Принцип суперпозиции сил

Принцип суперпозиции сил
Если на тело действует несколько сил, то их можно заменить одной равнодействующей силой, которая равна векторной сумме всех сил, действующих на тело:

Сложение сил
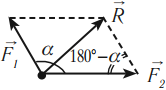
Равнодействующая сил равна геометрической сумме действующих на тело сил:

Силы направлены вдоль одной прямой:

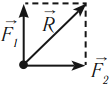
Силы направлены перпендикулярно друг другу:

Силы направлены под углом ​ \( \alpha \) ​ друг к другу:

Второй закон Ньютона

Второй закон Ньютона
Равнодействующая сил, приложенных к телу, равна произведению массы тела на сообщаемое ему ускорение:

Физический смысл закона:

• закон связывает кинематические и динамические характеристики одного и того же тела;
• закон утверждает, что будет происходить с телом, если на него действуют другие тела.

Важно!
Направление ускорения всегда совпадает с направлением равнодействующей сил. Второй закон Ньютона применим для сил любой природы.

Важно!
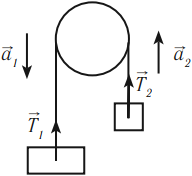
При рассмотрении движения связанных тел часто употребляется модель «невесомая нерастяжимая нить». Условие «невесомости» нити позволяет не рассматривать ее как отдельное тело и не писать для нее основное уравнение второго закона Ньютона. Поэтому силы натяжения нити, приложенные к связанным телам, оказываются равными по модулю. Условие «нерастяжимости» позволяет считать, что все связанные тела движутся с одинаковым ускорением:

Алгоритм применения второго закона Ньютона к решению задач

1. Запишите краткое условие задачи.
2. Определите характер движения.
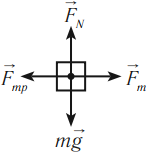
3. Сделайте рисунок, на котором укажите все силы, действующие на тело, направление векторов скорости и ускорения.
4. Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
5. Запишите второй закон Ньютона в векторной форме.
6. Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
7. Решите полученную систему уравнений относительно неизвестных величин.
8. Выполните действия с единицами измерения величин.
9. Запишите ответ.

Третий закон Ньютона

Третий закон Ньютона
Силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей центры этих тел:

Физический смысл закона:

• закон относится не к одному телу, а к системе тел;
• закон утверждает, что во всех случаях, когда одно тело действует на другое, имеет место не одностороннее действие, а взаимодействие тел;
• закон утверждает, что силы возникают парами, имеют одну и ту же природу, появляются и исчезают одновременно.

Важно!
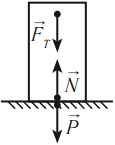
Несмотря на то, что эти силы равны и противоположны по направлению, они друг друга не компенсируют, т. к. приложены к разным телам. Компенсировать друг друга могут только силы, приложенные к одному и тому же телу, если они равны по модулю и противоположны по направлению. Например, утверждают, что коробка покоится на столе потому, что сила тяжести, действующая на тело, согласно третьему закону Ньютона равна по модулю и противоположна по направлению силе реакции опоры, действующей на нее со стороны стола.

На самом деле равенство ​ \( \vec_Т+\vec=0 \) ​ является следствием второго закона Ньютона, а не третьего. Ускорение равно нулю, поэтому и сумма сил, действующих на коробку, равна нулю. Из третьего же закона Ньютона следует, что сила реакции опоры равна по модулю весу коробки, т. е. силе, с которой коробка действует на стол. Эти силы приложены к разным телам и направлены в разные стороны.

Закон всемирного тяготения. Искусственные спутники Земли

Всякое тело, имеющее массу, является источником гравитационного поля – поля тяготения.

Закон всемирного тяготения
Два тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению масс этих тел, обратно пропорционален квадрату расстояния между ними и направлен вдоль линии, соединяющей эти тела:

где ​ \( G \) ​ – гравитационная постоянная.

Гравитационная постоянная численно равна силе притяжения между двумя телами массой по 1 кг, расположенными на расстоянии 1 м:

Закон справедлив для:

• материальных точек;
• однородных шаров;
• материальной точки и шара;
• концентрических тел.

Искусственный спутник Земли – это тело, которое обращается вокруг Земли.
Траектория движения искусственных спутников – эллипс, но мы для упрощения считаем, что они движутся по окружности.
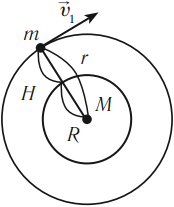
Линейная скорость такого движения есть первая космическая скорость.
Первая космическая скорость – это горизонтально направленная минимальная скорость, с которой тело могло бы двигаться вокруг Земли по круговой орбите, т. е. стать искусственным спутником Земли.

На рисунке ​ \( R \) ​ – радиус Земли, ​ \( H \) ​ – высота спутника над поверхностью Земли, ​ \( r \) ​ – высота орбиты спутника:

Период обращения искусственного спутника Земли можно рассчитать по формуле:

Вторая космическая скорость – это наименьшая скорость, которую надо сообщить телу, чтобы его орбита в поле тяготения Земли стала параболической, т. е. чтобы тело могло стать искусственным спутником Солнца:

Третья космическая скорость – это скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы:

Важно!
При решении задач следует помнить, что в законе всемирного тяготения расстояние берется от центра тела, а не от его поверхности.

Сила тяжести

Сила тяжести – это сила, с которой Земля притягивает к себе тела.

Сила тяжести равна произведению массы тела на ускорение свободного падения:

Точка приложения силы тяжести – центр тела.
Сила тяжести всегда направлена вертикально вниз.

Сила тяжести является частным случаем силы всемирного тяготения, поэтому

где ​ \( M \) ​ – масса Земли, ​ \( m \) ​ – масса тела, ​ \( R \) ​ – радиус Земли.

Ускорение свободного падения не зависит от массы тела, зависит от массы Земли и от расстояния от центра Земли до тела.

Важно!
У поверхности Земли ускорение свободного падения не везде одинаково. Оно зависит от географической широты: на полюсах больше, чем на экваторе. Дело в том, что земной шар немного сплюснут у полюсов. Экваториальный радиус Земли больше полярного на 21 километр.

Вес и невесомость

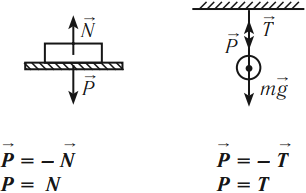
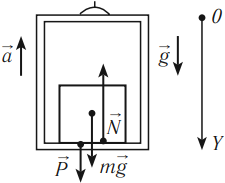
Вес – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

Обозначение – ​ \( P \) ​, единица измерения – Н.

Точка приложения веса – точка соприкосновения тела с опорой или подвесом. Вес тела всегда направлен против силы реакции опоры или силы натяжения. Модуль веса находится по третьему закону Ньютона.

Вес тела может изменяться:

• если тело покоится или движется прямолинейно и равномерно, то вес равен силе тяжести:

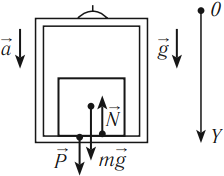
• если тело движется с ускорением, направленным вертикально вниз (движение вниз с ускорением или вверх с замедлением), то его вес меньше силы тяжести:

если тело движется вниз с ускорением, равным ускорению свободного падения, то тело находится в состоянии невесомости.
Невесомость – это исчезновение веса при движении опоры вниз с ускорением свободного падения:

• если тело движется с ускорением, направленным вертикально вверх (движение вверх с ускорением или вниз с замедлением), то его вес больше силы тяжести:

При таком движении тело испытывает перегрузку.
Перегрузка – это величина, которая показывает, во сколько раз вес тела, поднимающегося с ускорением или опускающегося с замедлением, больше его веса в состоянии покоя.
Обозначение – ​ \( n \) ​, единиц измерения нет:

Сила упругости. Закон Гука

Сила упругости – это сила, возникающая при деформации тела.

Деформация – это изменение формы и объема тела в результате неодинакового смещения различных его частей под действием силы.

• упругие – это деформации, при которых после прекращения действия внешних сил тело принимает первоначальные размеры и форму (растяжение, сжатие, изгиб, кручение, сдвиг);
• пластические – это деформации, которые сохраняются в теле после прекращения действия внешних сил.

Основные величины, характеризующие деформацию

• Абсолютное удлинение – изменение размеров тела под действием силы.

Обозначение – ​ \( x \) ​ или ​ \( \Delta \) ​, единицы измерения – м.

где ​ \( l_0 \) ​ – длина тела до действия силы (начальная длина),
​ \( l \) ​ – длина тела во время действия силы.

• Относительное удлинение – это количественная мера степени деформации тела.

Обозначение – ​ \( \varepsilon \) ​, единиц измерения нет.
Относительное удлинение равно отношению абсолютного удлинения к длине тела до действия силы (начальной длине тела):

• Механическое напряжение – это сила, действующая на единицу площади поперечного сечения.

Обозначение – ​ \( \sigma \) ​, единицы измерения – Па (Паскаль):

Закон Гука
Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена в сторону, противоположную деформации:

где ​ \( k \) ​ – жесткость пружины.

Знак «–» в законе Гука говорит о том, что сила упругости всегда направлена противоположно смещению частиц тела при деформации. При решении задач им можно пренебречь.

Виды силы упругости
Сила реакции опоры – это сила, действующая на тело со стороны опоры.
Обозначение – ​ \( N \) ​, единицы измерения – Н.
Сила натяжения – это сила, действующая на тело со стороны подвеса.
Обозначение – ​ \( T \) ​, единицы измерения – Н.

Важно!
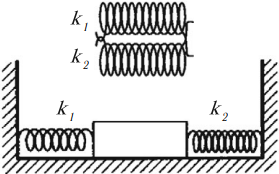
Соединения пружин:

Важно!
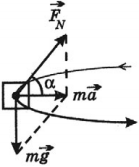
Если тело движется по окружности и нет силы трения между соприкасающимися поверхностями, то оно вынуждено наклоняться под углом к поверхности, по которой движется, иначе его центростремительное ускорение станет равным нулю и оно поедет по касательной к окружности согласно первому закону Ньютона. Чтобы удержаться на круге (сохранить равновесие), оно наклоняется к центру. В этом случае

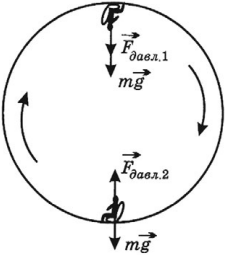
Если тело совершает мертвую петлю, то в верхней точке петли и сила тяжести, и сила нормального давления будут направлены вниз, поэтому

В нижней точке мертвой петли сила нормального давления направлена вверх и больше силы тяжести. В этом случае

Сила трения

Сила трения – это сила, возникающая при движении тел или при попытке сдвинуть их с места вследствие неровностей поверхностей соприкасающихся тел.

Сила трения действует на поверхности тел и затрудняет их перемещение относительно друг друга.
Сила трения всегда направлена противоположно относительному перемещению тела, т. е. против направления вектора скорости.

Виды трения

Внешнее трение (сухое) – это трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.

• Сила трения покоя – это сила, которая возникает между соприкасающимися и покоящимися относительно друг друга поверхностями, а также при попытке сдвинуть тело с места.

Сила трения покоя саморегулирующаяся, т. е. в зависимости от внешних воздействий она может меняться от 0 до максимального значения.

где ​ \( \mu \) ​ – коэффициент трения, ​ \( N \) ​ – сила реакции опоры.

Если в условии задачи не говорится, что сила трения покоя максимальна, то ее надо находить через другие силы по второму закону Ньютона.

• Cила трения скольжения – это сила, которая возникает между соприкасающимися и движущимися относительно друг друга телами.

• Сила трения качения – это сила, которая возникает между соприкасающимися и катящимися относительно друг друга телами.

Внутреннее трение (жидкое или вязкое) – между слоями жидкости или газа, скорости которых меняются от одного слоя к другому.

Если движение происходит по гладкой поверхности, то сила трения равна нулю.

Способы уменьшения трения:

• выравнивание соприкасающихся поверхностей;
• смазка;
• установка шариковых и роликовых подшипников.

Важно!
Сила трения не зависит от площади соприкосновения трущихся поверхностей. Она зависит от относительной скорости тел. В этом ее главное отличие от сил тяготения и упругости, зависящих только от координат.

Важно!
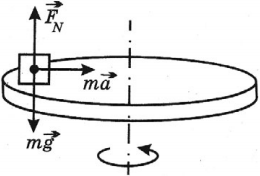
Если тело удерживается на горизонтальном вращающемся диске силой трения, то

Давление

Давление – это скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади этой поверхности.

Обозначение – ​ \( p \) ​, единицы измерения – Па (Паскаль):

1 Па – это давление, которое производит сила 1 Н на перпендикулярную к ней поверхность площадью 1 м 2 .

1 мм рт. ст. (миллиметр ртутного столба) = 133,3 Па.
1 атм (атмосфера) = 100 кПа.

Давление возрастает, если увеличивается сила давления или уменьшается площадь, на которую оказывается давление.
Давление уменьшается, если уменьшается сила давления или увеличивается площадь, на которую оказывается давление.

Тема 3.1. Основные понятия и аксиомы динамики

§1. Динамика точки. Основные понятия и определения.

В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.

В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.

Понятие о силе, как о величине, характеризующей меру механи­ческого взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоян­ными. Между тем, на движущееся тело наряду с постоян­ными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.

Сила – векторная физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть появляется ускорение, или происходит деформация тела, либо имеет место и то, и другое. В том случае, когда тело при взаимодействии получает ускорение, говорят о динамическом проявлении сил. В том случае, когда тело при взаимодействии деформируется, говорят о статическом проявлении сил.

Как показывает опыт, переменные силы могут определенным об­разом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при посте­пенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопро­тивления среды (воды, воздуха).

К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.

Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одина­ковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.

Количественной мерой инертности данного тела является фи­зическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

За единицу массы принят эталон – сплав платины и иридия, хранящийся в палате мер и весов в Париже: [m]=кг. Масса–величина аддитивная

и скалярная.

В общем случае движение тела зависит не только от его суммар­ной массы и приложенных сил; характер движения может еще зави­сеть от формы тела, точнее от взаимного расположения образующих его частиц (т.е. от распределения масс).

Под материальной точкой понимают материальное тело столь малых размеров, что различием в движении отдельных его точек можно пренебречь и положение которого можно определить координатами одной из его точек.

Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.

Наконец, материальными точками можно считать частицы, на кото­рые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.

Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.

При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.

§2. Законы динамики

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.

Первый закон (закон инерции), открытый Галилеем, гласит: существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано.

или в другой формулировке

если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое.

Движение, совершаемое точ­кой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи — пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоян­ной по модулю и направлению скоростью (