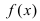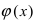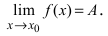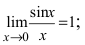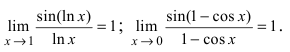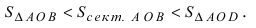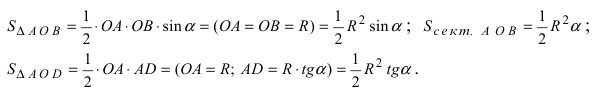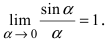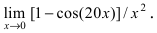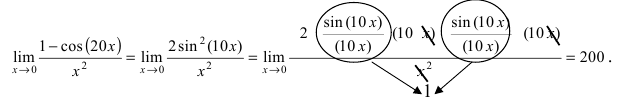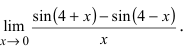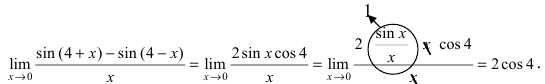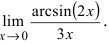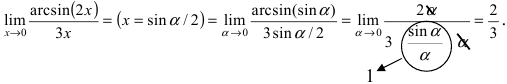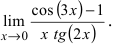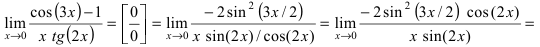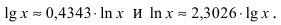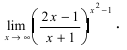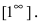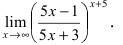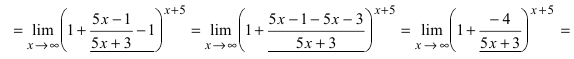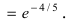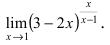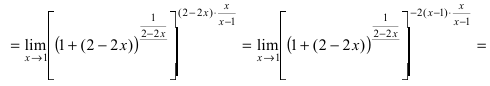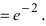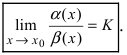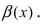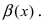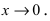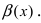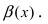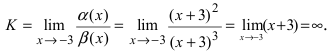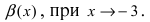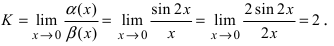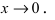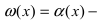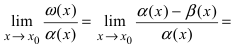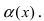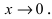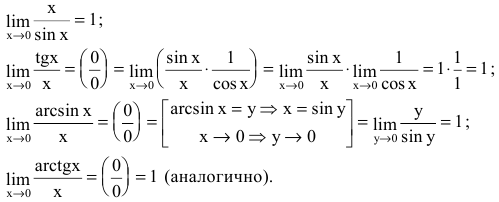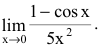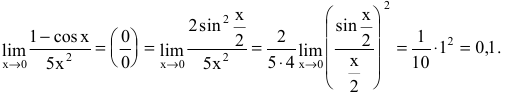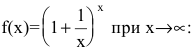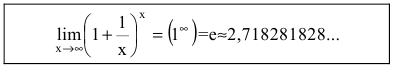Замечательные пределы
Термин «замечательный предел» широко используется в учебниках и методических пособиях для обозначения важных тождеств, которые помогают существенно упростить работу по нахождению пределов.
Но чтобы суметь привести свой предел к замечательному, нужно к нему хорошенько приглядеться, ведь они встречаются не в прямом виде, а часто в виде следствий, снабженные дополнительными слагаемыми и множителями. Впрочем, сначала теория, потом примеры, и все у вас получится!
Первый замечательный предел
Первый замечательный предел записывается так (неопределенность вида $0/0$):
Следствия из первого замечательного предела
Примеры решений: 1 замечательный предел
Решение. Первый шаг всегда одинаковый — подставляем предельное значение $x=0$ в функцию и получаем:
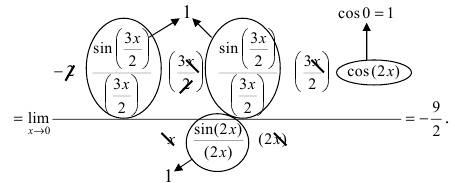
Получили неопределенность вида $\left[\frac<0><0>\right]$, которую следует раскрыть. Если посмотреть внимательно, исходный предел очень похож на первый замечательный, но не совпадает с ним. Наша задача — довести до похожести. Преобразуем так — смотрим на выражение под синусом, делаем такое же в знаменателе (условно говоря, умножили и поделили на $3x$), дальше сокращаем и упрощаем:
Выше как раз и получился первый замечательный предел: $$ \lim\limits_
Решение. Подставляем предельное значение $x=0$ в функцию и получаем:
Получили неопределенность вида $\left[\frac<0><0>\right]$. Преобразуем предел, используя в упрощении первый замечательный предел (три раза!):
Решение. А что если под тригонометрической функцией сложное выражение? Не беда, и тут действуем аналогично. Сначала проверим тип неопределенности, подставляем $x=0$ в функцию и получаем:
Получили неопределенность вида $\left[\frac<0><0>\right]$. Умножим и поделим на $2x^3+3x$:
Снова получили неопределенность, но в этом случае это просто дробь. Сократим на $x$ числитель и знаменатель:
Второй замечательный предел
Второй замечательный предел записывается так (неопределенность вида $1^\infty$):
$$ \lim\limits_
Следствия второго замечательного предела
Примеры решений: 2 замечательный предел
Решение. Проверим тип неопределенности, подставляем $x=\infty$ в функцию и получаем:
Получили неопределенность вида $\left[1^<\infty>\right]$. Предел можно свести к второму замечательному. Преобразуем:
Выражение в скобках фактически и есть второй замечательный предел $\lim\limits_
Решение. Подставляем $x=\infty$ в функцию и получаем неопределенность вида $\left[ \frac<\infty><\infty>\right]$. А нам нужно $\left[1^<\infty>\right]$. Поэтому начнем с преобразования выражения в скобках:
Выражение в скобках фактически и есть второй замечательный предел $\lim\limits_
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx<2<,>718281828459045>$. Если сделать замену $t=\frac<1>
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $\frac<1>
$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Сразу отметим, что основание степени (т.е. $\frac<3x+1><3x-5>$) стремится к единице:
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+\frac<1>
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
Продолжим «подгонку». В выражении $1+\frac<1>
Итак, основание степени, т.е. $1+\frac<1><\frac<3x-5><6>>$, подогнано под вид $1+\frac<1>
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac<3x-5><6>$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac<6><3x-5>$. Итак, имеем:
Отдельно рассмотрим предел дроби $\frac<6\cdot(4x+7)><3x-5>$, расположенной в степени:
Согласно формуле (1) имеем $\lim_
Полное решение без промежуточных пояснений будет иметь такой вид:
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $\frac<6><3x-5>\to<0>$ при $x\to\infty$, то применяя формулу (2), получим:
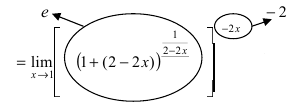
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $x\to<1>$, т.е. $\lim_
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $x\to<1>$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $x\to<1>$, то $
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $\frac<1>
Полное решение без пояснений таково:
Так как $\lim_
Так как $\sin^2x=\frac<1-\cos<2x>><2>$, то $\cos<2x>-1=-2\sin^2x$, поэтому:
Здесь мы учли, что $\lim_
Так как при $x>0$ имеем $\ln(x+1)-\ln
Раскладывая дробь $\frac
Так как $\lim_
Можно решить данный пример и по-иному, используя замену: $t=\frac<1>
Выясним, к чему стремится выражение $\frac<2x^2+3><2x^2-4>$ при условии $x\to\infty$:
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Замечательные пределы — определение и вычисление с примерами решения
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
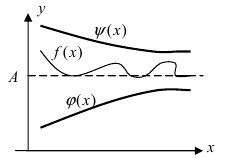
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции
значениями функций
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 
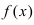
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 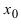
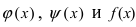
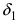
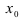
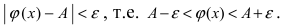
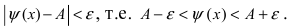
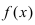
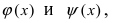
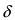
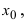
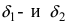
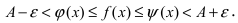
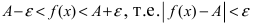
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 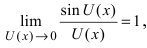
Пример:
Пределы являются первыми замечательными пределами
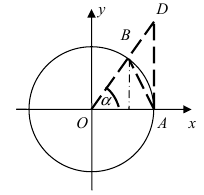
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 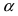
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 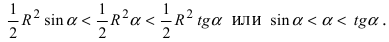
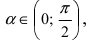
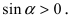
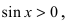
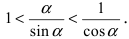
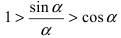
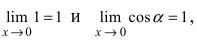
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 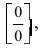
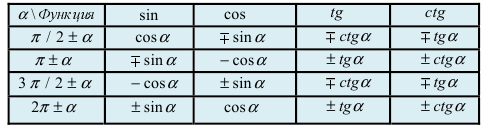
При вычислении первого замечательного предела используют следующие формулы:
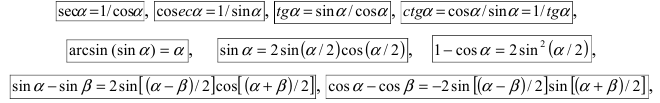
Табл. 1. Значения синуса и косинуса на интервале
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 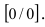
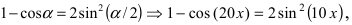
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 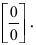
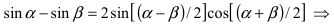
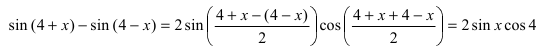
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 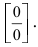
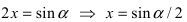
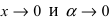
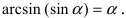
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 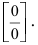
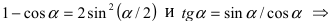
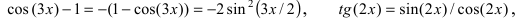
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 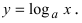
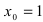
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 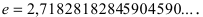
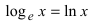
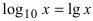
Определение: Вторым замечательным пределом называется предельное равенство 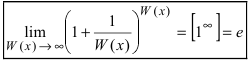
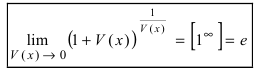
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 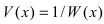
Замечание: Наличие неопределенности 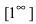
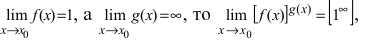
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
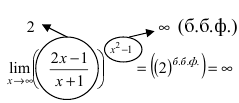
Пример:
Найти lim
Решение:
При подстановке предельного значения переменной х имеем неопределенность 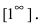
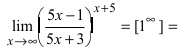
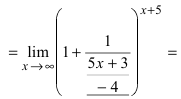
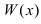
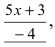
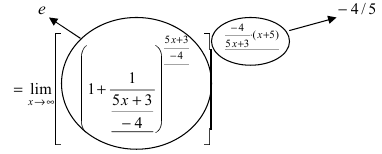
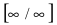
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 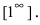
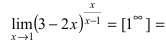
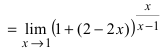
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 
Определение: Если предел К не существует, то бесконечно малые функции 
Пример:
Пусть 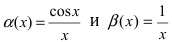
Решение:
Для доказательства вычислим предел 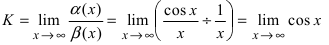
Определение: Если предел К равен нулю, то бесконечно малая функция 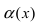
Пример:
Пусть 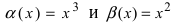
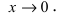
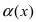
Решение:
Для доказательства вычислим предел 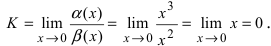
Определение: Если предел К равен 
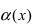
Пример:
Пусть 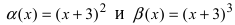
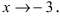
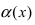
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 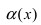
Определение: Если предел К равен конечному числу 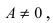
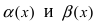
Пример:
Пусть 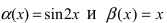
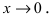
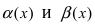
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 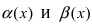
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 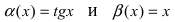
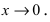
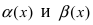
Решение:
Вычислим предел 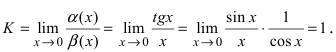
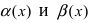
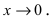
Теорема: Для того чтобы бесконечно малые функции 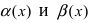
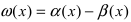
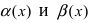
Доказательство:
1. Необходимость. Пусть бесконечно малая функция 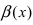
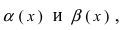
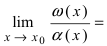
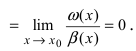
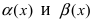
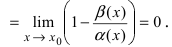
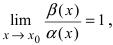
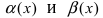
2. Достаточность. Пусть бесконечно малые функции 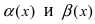
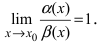
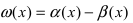
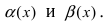
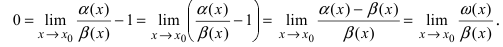
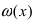
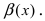
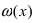
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 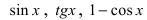
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
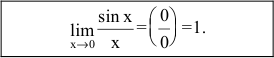
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
(Для запоминания: 2
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://math1.ru/education/limits/limitsecond.html
http://www.evkova.org/zamechatelnyie-predelyi