Замена косинуса на синус в уравнении

Формулы перехода от синуса к косинусу

Определения синуса, косинуса, тангенса и котангенса.

Знаки тригонометрических функций:

Значения тригонометрических функций

Формулы синуса, косинуса, тангенса и котангенса угла (–α):

sin (–α) = – sin α
cos (–α) = cos α
tg (–α) = – tg α
ctg (–α) = – ctg α

Все формулы приведения можно получить, пользуясь следующими правилами:
1. В правой части формулы ставится тот знак, который имеет левая часть при условии

2. Если в левой части формулы угол равен /2 ± или 3/2±, то синус заменяется на косинус, тангенс на котангенс и наоборот, если угол равен ± или 2k±, то замены не происходит.

Формулы двойного угла.

Формулы перехода от суммы к произведению.

Формулы перехода от произведения к сумме.

Формулы понижения степени.

Преобразование выражения a·cos + b·sin путем введения вспомогательного аргумента.

,

где вспомогательный аргумент определяется из условий

Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin – α + 2 π z = – sin α , cos – α + 2 π z = cos α t g – α + 2 π z = – t g α , c t g – α + 2 π z = – c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = – sin α t g π 2 + α + 2 π z = – c t g α , c t g π 2 + α + 2 π z = – t g α sin π 2 – α + 2 π z = cos α , cos π 2 – α + 2 π z = sin α t g π 2 – α + 2 π z = c t g α , c t g π 2 – α + 2 π z = t g α sin π + α + 2 π z = – sin α , cos π + α + 2 π z = – cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π – α + 2 π z = sin α , cos π – α + 2 π z = – cos α t g π – α + 2 π z = – t g α , c t g π – α + 2 π z = – c t g α sin 3 π 2 + α + 2 π z = – cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = – c t g α , c t g 3 π 2 + α + 2 π z = – t g α sin 3 π 2 – α + 2 π z = – cos α , cos 3 π 2 – α + 2 π z = – sin α t g 3 π 2 – α + 2 π z = c t g α , c t g 3 π 2 – α + 2 π z = t g α

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β – sin α · sin β cos α – β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = – 1 ± c t g α · c t g β c t g α ± c t g β

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α – sin 2 α , cos 2 α = 1 – 2 sin 2 α , cos 2 α = 2 cos 2 α – 1 t g 2 α = 2 · t g α 1 – t g 2 α с t g 2 α = с t g 2 α – 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α – sin 3 α , sin 3 α = 3 sin α – 4 sin 3 α cos 3 α = cos 3 α – 3 sin 2 α · cos α , cos 3 α = – 3 cos α + 4 cos 3 α t g 3 α = 3 t g α – t g 3 α 1 – 3 t g 2 α c t g 3 α = c t g 3 α – 3 c t g α 3 c t g 2 α – 1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin 2 α 2 = 1 – cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 – cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 – cos α

Формулы понижения степени

sin 2 α = 1 – cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α – sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 – 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

sin n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 ( – 1 ) n 2 – k · C k n · cos ( ( n – 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 C k n · cos ( ( n – 2 k ) α )

sin n α = 1 2 n – 1 ∑ k = 0 n – 1 2 ( – 1 ) n – 1 2 – k · C k n · sin ( ( n – 2 k ) α ) cos n α = 1 2 n – 1 ∑ k = 0 n – 1 2 C k n · cos ( ( n – 2 k ) α )

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sin α + sin β = 2 sin α + β 2 · cos α – β 2 sin α – sin β = 2 sin α – β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α – β 2 cos α – cos β = – 2 sin α + β 2 · sin α – β 2 , cos α – cos β = 2 sin α + β 2 · sin β – α 2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.

Формулы произведения тригонометрических функций

sin α · sin β = 1 2 · ( cos ( α – β ) – cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α – β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α – β ) + sin ( α + β ) )

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции – синус, косинус, тангенс и котангенс, – могут быть выражены через тангенс половинного угла.

Универсальная тригонометрическая подстановка

sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 – t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 – t g 2 α 2 c t g α = 1 – t g 2 α 2 2 t g α 2

Тригонометрические формулы

Тригонометрические формулы основаны на тригонометрических функциях (ТФ) углов.

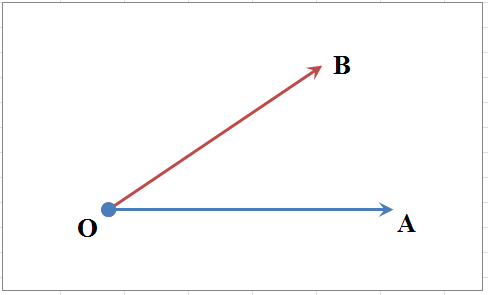
Угол – есть фигура, образованная двумя двумя лучами $OA$ и $OB$ (стороны угла), исходящими из одной точки $O$ (вершина угла).

Мерой угла служит величина поворота вокруг вершины $O$, переводящего луч $OA$ в положение $OB$.

Распространены две системы измерения углов: градусная и радианная.

В градусной системе измерения углов за единицу принимается поворот луча на $1/360$ часть одного полного оборота — градус (обозначение $<>^circ $). Полный оборот составляет, таким образом, $360<>^circ $. Градус делится на 60 минут (обозначение $’$); минута — на 60 секунд (обозначение $”$).

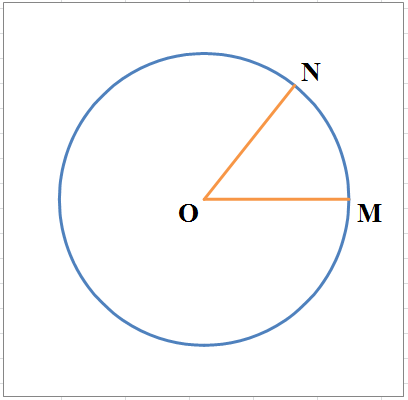
В радианной системе измерения углов за единицу измерения принимается острый угол ($MON$), под которым видна из центра окружности её дуга $MN$, равная радиусу ($mathop limits^ =OM$). Такой угол называется радианом.

Теперь допустим, что угол $MON$ — произвольный. Тогда радианная мера этого угла равна отношению длины дуги $mathop limits^ $, описанной произвольным радиусом из центра $O$ и заключенной между сторонами угла, к радиусу $OM$ этой дуги.

Попробуй обратиться за помощью к преподавателям

Мера угла считается положительной, если вращение луча (радиуса $OM$) совершается против часовой стрелки, и отрицательной — в противном случае.

Переход от одного измерения к другому осуществляется по формулам: $alpha <>^circ =frac

cdot alpha$ или $alpha =frac

cdot alpha <>^circ $.

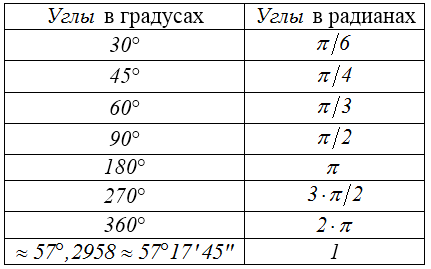
Полезно помнить следующую таблицу градусной и радианной меры некоторых часто встречающихся углов:

Определение синуса, косинуса и тангенса, знаки синуса, косинуса и тангенса

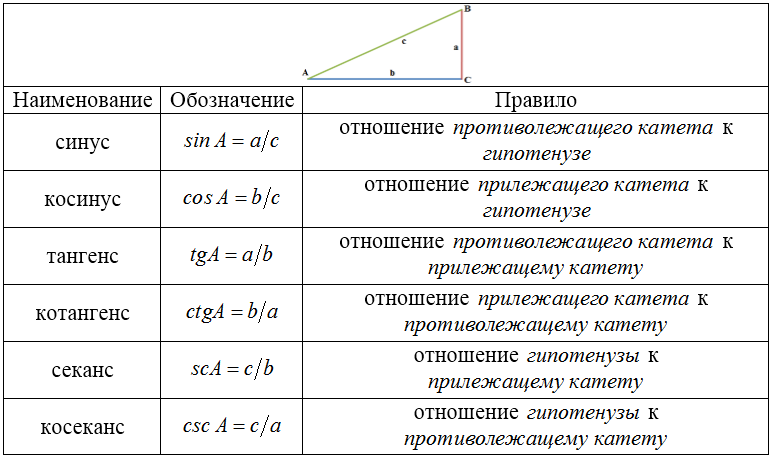
ТФ острого угла можно определить из прямоугольного треугольника:

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Из этой таблицы видно, как через синус и косинус можно выразить все остальные функции: $tgA=frac $; $ctgA=frac $; $scA=frac $; $csc A=frac $.

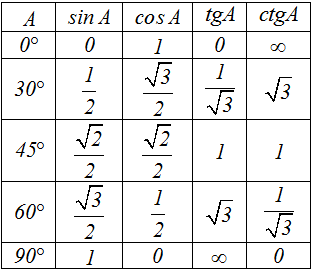
Полезно помнить значения основных ТФ для часто встречающихся значений углов:

ТФ приписывается определенный знак в зависимости от того, в какой четверти тригонометрического круга лежит подвижный радиус $OC$, образующий угол с неподвижным радиусом $OA$:

Обратные тригонометрические функции (ОТФ)

ОТФ называются угловые величины $y$ (в радианах), определяемые следующими равенствами и указываемые с прописной буквы:

$y=Arcsin x$, если $x=sin y$ — арксинус;

$y=Arccos x$, если $x=cos y$ — арккосинус;

$y=Arctgx$, если $x=tgy$ — арктангенс;

$y=Arcctgx$, если $x=ctgy$ — арккотангенс.

ОТФ многозначны. Поэтому из всего множества значений каждой из них выделяют главные, а наименования указывают со строчной буквы:

Универсальная тригонометрическая подстановка, вывод формул, примеры

Данная статья посвящена разбору такой темы, как универсальная тригонометрическая подстановка. Суть данного термина состоит в том, что мы находим значение любой тригонометрической функции ( sin α , cos α , t g α , c t g α ) через формулу тангенса половинного угла. Этот вариант намного проще и рациональнее, так как выполнять дальнейшие вычисления легче без корней, а с целыми числами.

Мы подробно рассмотрим этот раздел. Для начала мы расскажем вам о формулах тангенса половинного угла, которой мы будем часто пользоваться. После мы перейдем к практическому применении формул, рассмотрим несколько примеров использования универсальной тригонометрической подстановки.

Универсальная тригонометрическая подстановка для sin α , cos α , t g α , c t g α

Во введении мы рассказали, что основной темой этого раздела станет основная тригонометрическая подстановка. Для начала запишем и разберем формулы, с помощью которых можно выразить sin α , cos α , t g α , c t g α через тангенс половинного угла α 2 .

sin α = 2 · t g α 2 1 + t g 2 α 2 , cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 · t g α 2 1 — t g 2 α 2 , c t g = 1 — t g 2 α 2 2 · t g α 2

Указанные формулы будут правильны для всех углов α . Для работы в задаче должен быть определен входящие тангенсы и котангенсы.

Формулы для sin α и cos α , sin α = 2 · t g α 2 1 + t g 2 α 2 и cos α = 1 — t g 2 α 2 1 + t g 2 α 2 имеют место для a ≠ π + 2 π · z , где z – любое целое число, так как при a = π + 2 π · z , t g α 2 не определен.

Формула t g α = 2 · t g α 2 1 — t g 2 α 2 справедлива для α ≠ π 2 + π · z и a ≠ π + 2 π · z , так как при a = π 2 + π · z не определен t g α Знаменатель дроби обращается в нуль, а при α = π + 2 π · z не определен t g α 2 .

Формула c t g = 1 — t g 2 α 2 2 · t g α 2 , выражающая c t g через t g α 2 , справедлива для a ≠ π · z , так как при a = π · z не определен c t g , при a = π + 2 π · z не определен t g α 2 , а при α = 2 π · z знаменатель дроби обращается в нуль.

Вывод формул

Разберем вывод формул, выражающих sin α , cos α , t g α , c t g α через тангенс половинного угла. Начнем с формул для синуса и косинуса. Представим синус и косинус по формулам двойного угла как sin α = 2 · sin α 2 · cos α 2 и cos α = cos 2 α 2 — sin 2 α 2 соответственно. Теперь выражения 2 · sin α 2 · cos α 2 и cos 2 α 2 — sin 2 α 2 запишем в виде дробей со знаменателем 1 как 2 · sin α 2 · cos α 2 1 и cos 2 α 2 — sin 2 α 2 1 . Воспользуемся основным тождеством из тригонометрии и заменим единицы в знаменателе на сумму квадратов sin и cos , после чего получаем 2 · sin α 2 · cos α 2 sin 2 α 2 + cos 2 α 2 и cos 2 α 2 — sin 2 α 2 sin 2 α 2 + cos 2 α 2

Для решения данного выражения необходимо числитель и знаменатель полученных дробей разделить на cos 2 α 2 (его значение не равно нулю при условии α ≠ π + 2 π · z ). Вся формула будет выглядеть так sin α = 2 · sin α 2 · cos α 2 = 2 · sin α 2 · cos α 2 sin 2 α 2 + cos 2 α 2 = 2 · sin α 2 · cos α 2 cos 2 α 2 sin 2 α 2 + cos 2 α 2 cos 2 α 2 = 2 · sin α 2 cos α 2 sin 2 α 2 с os 2 α 2 + cos 2 α 2 с os 2 α 2 = 2 · t g α 2 t g 2 α 2 + 1

и cos α = cos 2 α 2 — sin 2 α 2 = c os 2 α 2 — sin 2 α 2 1 = c os 2 α 2 — sin 2 α 2 sin 2 α 2 + c os 2 α 2 = = cos 2 α 2 — sin 2 α 2 c os 2 α 2 sin 2 α 2 + c os 2 α 2 c os 2 α 2 = cos 2 α 2 cos 2 α 2 — sin 2 α 2 cos 2 α 2 sin 2 α 2 c os 2 α 2 + cos 2 α 2 c os 2 α 2 = 1 — t g 2 α 2 t g 2 α 2 + 1

Мы закончили вывод формул для sin и cos , завершив все вычислительные действия.

Следующий шаг – это вывод определенных формул для нахождения t g и c t g .

Взяв за основу описанные выше примеры t g α = sin α cos α и c t g α = cos α sin α , мы сразу получаем формулы, которые выражают тангенс и котангенс через тангенс половинного угла:

t g α = sin α cos α = 2 · t g α 2 1 + t g 2 α 2 1 — t g 2 α 2 1 + t g 2 α 2 = 2 · t g α 2 1 — t g 2 α 2 ;

c t g α = cos α sin α = 1 — t g 2 α 2 1 + t g 2 α 2 2 · t g α 2 1 + t g 2 α 2 = 1 — t g 2 α 2 2 · t g α 2 ;

В этом разделе мы нашли все формулы, которые нам потребуются для выражения основных тригонометрических функций.

Примеры использования в задачах и упражнениях

Для начала рассмотрим пример применения универсальной тригонометрической подстановки при преобразовании выражений.

Необходимо привести 2 + 3 · cos 4 α sin 4 α — 5 к примеру, который содержит только одну функцию t g 2 α .

В данном упражнении мы также воспользуемся универсальной подстановкой, которая является одним из важных правил тригонометрии. Применим к косинусу и синусу 4 α те самые формулировки, которые выражают основные функции через тангенс половинного угла. Получив сложное выражение, нам остается только его упростить.

2 + 3 · cos 4 α sin 4 α — 5 = 2 + t g 2 2 α t g 2 2 α + 1 2 · t g 2 α t g 2 2 α + 1 — 5 = 2 · t g 2 2 α + 2 + 3 — 3 · t g 2 2 α t g 2 2 α + 1 2 · t g 2 α — 5 · 2 · t g 2 2 α — 5 t g 2 2 α + 1 = t g 2 2 α — 5 5 · t g 2 2 α — 2 · t g 2 α + 5

2 + 3 · cos 4 α sin 4 α — 5 = t g 2 2 α — 5 5 · t g 2 2 α — 2 · t g 2 α + 5 .

Вспомним, что во введении мы подробно рассказали, как менять sin α , cos α , t g α , c t g α в частных случаях. Она заключается в том, чтобы преобразовать первоначальное рациональное выражение, содержащее sin , cos , t g и c t g , к выражению с одной функцией благодаря формуле. Это намного проще и понятнее. Мы выражаем все формулы через t g половинного угла. Данное преобразование обязательно пригодится при решении разнообразных уравнений и задач, интегрировании основных функций sin α , cos α , t g α , c t g α .

Алгебра

План урока:

Замена переменной

Пусть необходимо решить тригонометрическое уравнение

Это уравнение уже не является простейшим. Однако если заменить выражение 2х новой переменной (обозначим ее как t), то мы получим уже знакомое нам ур-ние:

Формула его корней выглядит так:

У нас есть формула, по которой можно вычислить значения t. Теперь произведем обратную замену:

Поделим это равенство на 2 и получим решение ур-ния:

Аналогичным путем можно решить любое уравнение вида

Где Т – какая-то тригонометрическая функция, k, b и a – некоторые числа.

Задание. Найдите решение тригонометрического уравнения

и выпишите его первые три положительных корня.

Решение. Введем переменную t = 3x + π/6, тогда ур-ние примет вид:

Далее следует обратная замена:

Получили формулу корней. Теперь надо найти три наименьших положительных корня. Напомним, что тригон-кое ур-ние имеет бесконечное количество корней, но каждый из них соответствует какому-либо целому числу n. Это соответствие как раз и задается формулой корней. Достаточно лишь выбрать какое-нибудь целое число n и подставить его в формулу корней. При этом большим значениям n соответствуют большие корни.

Выберем n = 0 и получим

Это положительный корень, но является ли он наименьшим? Проверим n = – 1:

Это отрицательное число. Значит, при n ≤– 1 получаются отрицательные корни, а при n ≥ 0 корни будут положительны. Нам нужны три наименьших положительных корня, им соответствуют значения n, равные 0, 1 и 2. Ноль мы уже подставляли в формулу корней, теперь подставим единицу и двойку:

Подставлять надо целые числа, потому что именно целым числам соответствуют корни уравнения. После формулы корней в ответах делается приписка «n∈ Z», или «где n – целое число».

Примечание. Записывая общее решение тригонометрических ур-ний (то есть серию корней), мы везде делаем приписку «n∊Z», которая означает, что n– это произвольное целое число. В будущем в промежуточных выводах мы ее делать не будем, так как она всегда подразумевается. Однако при решении учебных заданий, в том числе и на экзаменах, в ответе надо обязательно дописывать эту фразу, иначе оценка может быть снижена.

Заметим, что часто в простых случаях новую переменную не записывают явно, чтобы сделать решение более простым.

Задание. Решите ур-ние

Решение. Ур-ние cosx = – 1 является частным случаем, у которого решение записывается так:

Тогда для ур-ния cos (2x– π/4) = – 1 можно написать

Задание. Решите ур-ние

Решение. Слева стоит произведение двух скобок, а справа – ноль. Произведение будет равняться нулю лишь в том случае, когда хотя бы один из его множителей будет нулевым, то есть:

Вычислить arcsin 1/3 и arccos (– 2/5) мы не можем, так как чисел 1/3 и 2/5 нет в тригонометрических таблицах, поэтому оставляем решения в таком виде.

Теперь рассмотрим чуть более сложный случай, когда в качестве новой переменной принимают саму тригонометрическую функцию.

Задание. Решите уравнение методом замены переменной

Решение. Здесь за переменную можно принять величину sinx:

Получили обычное квадратное уравнение! Решим его, найдя дискриминант

У нас есть два значения t. Можно произвести обратную замену неизвестного:

Получили два тригонометрических уравнения. Второе из них решений не имеет, ведь область значений синуса – это промежуток [– 1; 1], то есть ни при каких х он не может быть равен двум. Решим первое уравнение:

Применение формул для преобразования уравнений

Когда в уравнении стоят различные тригонометрические функции, то замена одной из них переменной не помогает найти корни ур-ния. В таких случаях требуется использовать тригонометрические формулы, чтобы получилось ур-ние, содержащее только одну тригонометрическую функцию.

Задание. Решите ур-ние

Решение. В уравнении стоят две различные тригонометрические функции – синус и косинус. Следует упростить левую часть, чтобы в ней осталась только одна функция. Вспомним основное тригонометрическое тождество:

С его помощью можно выразить величину sin 2 x:

Теперь подставим эту формулу в исходное ур-ние:

Далее раскрываем скобки и приводим подобные слагаемые:

Получили обычное уравнение с заменой переменной. Из него с помощью замены t = cosx получаем квадратное ур-ние:

Производим обратную замену:

Каждое из этих ур-ний имеет решение. Начнем с первого из них:

Арккосинус от отрицательного числа найдем отдельно, используя формулу

Подставляем вместо а число 0,5:

Тогда решение ур-ния cosx = – 0,5 примет вид:

Теперь решим второе ур-ние:

Задание. Решите ур-ние

Решение. Перенесем все выражения в левую часть:

Можно заметить, что теперь в левой части стоит выражение, которое похоже на формулу синуса разности двух углов:

Действительно, если в формулу подставить значения α = 5х и β = 3х, то мы получим левую часть ур-ния. Это значит, что ур-ние можно переписать в виде:

Задание. Решите ур-ние

Решение. Сначала заменим синус двойного угла:

Далее вынесем за скобки множитель 2sinx:

В скобках осталось выражение, которое, согласно основному тригонометрическому тождеству, равно единице:

Задание. Решите ур-ние

Решение. Заменим cos2x, используя формулу косинуса двойного угла:

теперь избавимся от соs 2 x:

Вводим переменную t = sinx:

Выполняем обратную замену:

Запишем их решения:

Задание. Решите ур-ние

и укажите те корни, которые принадлежат промежутку [– 2π; – π].

Решение. Преобразуем обе части, используя формулу косинуса двойного угла, а также формулу приведения sin (x + π/2) = cosx:

И снова вводим новую переменную cosx = t:

Выполняем обратную замену

Так как arccos (– 0,5) = π – arccos 0,5 = π– π/3 = 2π/3, то решениями этих ур-ний будут серии:

Первая часть задания выполнена. Теперь следует отобрать корни, попадающие в промежуток [– 2π; – π]. Сначала для удобства разобьем первую серию решений на две:

Подставим в серии решений число n = 0:

Получили три корня, которые больше, чем (– π), а потому располагаются на координатной прямой правее промежутка [– 2π; – π].Значит, нет смысла проверять ещё большие значение n, ведь им будут соответствовать ещё большие значения х. Будем подставлять отрицательные значения n до тех пор, пока не получим корни, меньшие (– 2π). При n = – 1 имеем:

Корни х₁ и х₂ попадают в промежуток [– 2π; – π]. Теперь подставим n = – 2:

Все три полученных значения меньше, чем (– 2π), то есть они не входят в нужный нам промежуток. Нет смысла подставлять другие значение n (– 2, – 3, – 4 …), так как будут получаться ещё меньшие корни. В итоге только два корня, (– 4π/3) и (– 2π), принадлежат промежутку [– 2π; – π].

Иногда в ур-нии стоят тригонометрические функции от разных углов. В этом случае приходится использовать формулы суммы или разности аргументов.

Задание. Решите ур-ние

Решение. Разложим выражения sin (π/3 – х) и sin (π/6 – х), используя формулу синуса и косинуса разности:

Тогда левая часть ур-ния примет вид:

Здесь мы просто левую часть, в которой большое выражение стоит, заменяем

А то, что такую замену можно сделать, мы доказали в решении до этого, используя формулы разности.

Соответственно, всё уравнение можно переписать так:

Однородные тригонометрические уравнения

Особый интерес представляют уравнения вида

где а и b – некоторые постоянные числа, не равные нулю. Такие ур-ния называют однородными уравнениями 1-ой степени. Приведем несколько примеров таких ур-ний:

Для решения таких ур-ний обе части делят на cosx:

Обратите внимание, что при выводе этой формулы мы делили ур-ние на cosx. Однако это выражение может быть равным нулю, а деление на ноль запрещено. Это значит, что мы должны быть уверены, что у ур-ния нет такого корня х, что соs х = 0. Уверены ли мы в этом?

Заметим сразу, что функции у = sinx и у = cosx обращаются в ноль в различных точках. Поэтому, если сosx = 0, то sinx ≠ 0, а значит, и всё выражение

не равно нулю. Поэтому мы можем спокойно делить такое ур-ние на соsx.

Задание. Решите ур-ние

Решение. Делим обе части на соsх и получаем:

Задание. Решите ур-ние

Решение. Можно составить две формулы приведения:

С их учетом исходное ур-ние примет вид:

Делим ур-ние на cos 2x:

Существуют и более сложные однородные уравнения второй степени. В общем случае они имеют вид:

Для того, чтобы решить их, необходимо поделить обе части на cos 2 x, и тогда мы получим равносильное ур-ние:

Произведя замену tgx = t, получим квадратное уравнение

Задание. Решите ур-ние

Решение. Поделим обе части на выражение cos 2 x:

Введем переменную tgx = t:

Возвращаемся к переменной х:

Введение вспомогательного угла

В правой части однородного ур-ния стоит ноль. Усложним задачу и рассмотрим схожие ур-ния, у которых справа стоит произвольное число, которое может быть и отлично от нуля. То есть ур-ние имеет вид

Существует ли универсальный метод решения тригонометрических уравнений такого вида? Да, существует, и называется он методом вспомогательного угла. Очевидно, что величина a 2 + b 2 является положительной, ведь это сумма квадратов чисел, отличных от нуля. Это значит, что существует действительное число

которое больше нуля.

Поделим ур-ние на N и получим новое ур-ние

Для краткости введем новые обозначения:

коэффициенты уравнения запишем большими буквами, чтобы не писать корни.

и тогда ур-ние примет более простой вид:

Попытаемся найти величину А 2 + В 2 :

Так как величина А 2 + В 2 равна единице, то можно подобрать такой угол α, что будут одновременно выполняться равенства

Угол α называют вспомогательным углом. Как его подобрать? Из равенства А = sinα очевидно, что

Заменим в (1) числа А и В по формулам (2) и (3) и получим:

Теперь слева стоит косинус разности, который можно «свернуть»:

Это уже почти что простейшее тригонометрическое уравнение, которое мы сможем решить.

Задание. Решите ур-ние

Решение. Коэффициенты перед синусом и косинусом равны 5 и 12. Найдем корень из суммы 5 2 + 12 2 :

Значит, число N = 13. Поделим ур-ние на 13:

Теперь введем вспомогательный угол α = arcsin 5/13. Тогда

Подставим в (1) вместо дробей 5/13 и 12/13 sinα и cosα:

Теперь смотрим в тригонометрические формулы сложения и вычитания аргументов. Есть ли там что-то похожее на левую часть ур-ния? Действительно, там есть следующая формула:

Наше ур-ние похоже на эту формулу, но надо поменять местами вычитаемое и уменьшаемое. Для этого можно умножить ур-ние на (– 1):

Уравнения с ограничениями на значение переменной

До этого мы рассматривали случаи, при которых переменная х могла принимать любые значения в уравнении. Однако, если в ур-нии переменная стоит под знаком корня или находится в знаменателе, то возникают некоторые ограничения на те значения, которые она может принимать. Рассмотрим пример.

Задание. Решите ур-ние

Решение. В левой части произведение двух множителей, а справа – ноль, следовательно, можно записать:

Решение для первого уравнения запишем в виде двух серий, а не одной (так проще будет проводить дальнейшее исследование). Сначала вычислим арксинус:

Тогда получаем три серии решений:

Теперь учтем, что в исходном уравнении выражение cosx стоит под корнем, поэтому должно соблюдаться условие:

Косинус принимает положительные значения в I и IV четверти. Отметим все серии решении на единичной окружности и посмотрим, какие из них попадают в I и IV четверть:

Теперь мы видим, что корни из серии 4π/3 + 2πn находятся в III четверти, то есть для них соsx 2 x = ctgx