Дифференциальное однородное уравнение: особенности и решение
Проанализируем один из важных классов дифференциальных уравнений, решающихся сведением к методу разделения переменных за счет подстановки — однородные уравнения. Затронем методы решения линейных уравнений, которые часто путают с однородными.
Однородные уравнения
Для начала дадим определение. F — однородная в том случае, если для нее верно равенство f(kx, ky) = f(x, y), где k — любое ненулевое число. Примеры однородной функции:
| F = | g 3 +r 3 | A = | d 2 + w 2 |
| 3g 3 + 5r 2 g | 2dw |
Чтобы убедиться в их однородности, достаточно аргументы функции F или A умножить на какой-либо коэффициент и посмотреть, не сократится ли он.
Замена e(t) = f(1, t)
Выше говорилось о том, что дифференциальные уравнения с однородными функциями сводятся к разделяющимся за счет замены. Для объяснения этого рассмотрим лемму.
Лемма 1. Если w — однородная функция первой степени с аргументами x и y, то верно тождество w(x, y) = e(y/x), при этом e(t) = f(1, t).
Доказывается данная лемма тривиальным образом: для этого просто нужно положить k = 1/x для всех ненулевых x.
Применение замены в решение y’ = f(x, y)
Допустим, у нас есть y’ = f, где f — однородная функция. Для решения однородного дифференциального уравнения на основе леммы 1 мы можем представить y’ = e(y/x). Уравнение разрешимо путем разделения переменных. Положим y/x = v — искомая функция. Значит y = xv, а y’ = v + xv’. Получим уравнение вида v + xv’ = e(v) или xv’ = e(v) — v.
Рассмотрим его подробнее. В данном случае решениями уравнения являются все значения v = vn — точки, в которых функция [e(v) — v] обращается в ноль. Соответственно, значения yn = vnx — являются решением y’ = e(y/x). В области значений, где [e(v) — v] не обращается в ноль, можно применить разделение переменных. То есть:
| dv | = | dx |
| -v + e(v) | x |
Интегрируя, получим решение E = ln|x| + C.
Заметка
Рассмотрим, почему вышеописанная замена работает при решении однородных дифференциальных уравнений. Для этого возьмем общее решение E = ln|x| + C и заменим x на kx и y на ky: E = ln|kx| + C = ln(k) + ln|x| + C. В свою очередь выражение ln(k) + C может быть представлено как W, и тогда решение будет выглядеть как E = ln|x| + W.
Получается, что замена x на kx и y на ky приводит лишь к замещению одного решения другим, но из того же класса. Иными словами, другое решение также удовлетворяет исходному уравнению. Описанное свойство на координатной плоскости называется гомотетией, т. е. интегральные кривые однородных дифференциальных уравнений переходят друг в друга.
Пример 1
Дано уравнение l 2 + ml + m 2 l’ + m 2 = 0. Найдем его решение. Неопытный глаз может по ошибке торопливо заключить, что данное уравнение не однородно, так как подстановка km вместо m и kn вместо n не дает исходное уравнение. Ошибка в данном случае заключается в том, что уравнение предварительно не было разрешено относительно производной n’. Сделаем.
| l’ = | (-1) | l 2 +ml+m 2 |
| m 2 |
В данном виде легко определить, что уравнение однородно.
| f(km, kl) = | (-1)[(km) 2 + (kl) 2 + k 2 ml] | = | (-1)(l 2 +ml+m 2 )k 2 | = | f(m, l) |
| (km) 2 | m 2 k 2 |
Приступим к решению, совершив замену l/m = v. Получим l = vm и l’ = mv’ + v. Подставим эти значения в уравнение:
| mv’ + v = | (-1)[m 2 + (vm) 2 + m(vm)] | = | (-1)(v 2 m 2 +m 2 v+m 2 ) | = 1 — v 2 — v |
| m 2 | m 2 |
Получим mv’ = — (v+1) 2 . Очевидно, что точка -1 — ‘nj решение уравнения, а до замены n = -m. При v+1 не равном нулю разделим переменные:
| — | dv | = | dm |
| (v+1) 2 | m |
Из получившегося уравнения в дифференциальной форме легко находится общий интеграл:
| ln|Cm| | = | 1 |
| 1+v |
Проведем обратную замену:
| n | = | m — m*ln|Cm| |
| ln|Cm| |
Также следует не забывать о найденном ранее решение n = -m.
Линейные дифференциальные уравнения
Часто однородные дифференциальные уравнения путают с линейными. Для полноты вопроса рассмотрим немного и этот класс. Итак, линейным называется дифференциальное уравнение, в котором функция и ее производная располагаются в линейной зависимости, т. е. получаем уравнение, которому присущ следующий вид:
w, o, e — представляют собой какие-либо функции.
Для разрешения этого уравнения относительно y’ необходимо рассмотреть все корни o(x). Положим, что для некоторого числа o(x0) = 0, тогда одним из решений описанного уравнение будет x0, т.к. получаем o(x0)dy = 0 и dx = 0. Это становится очевидным, если записать дифференциальную форму уравнения, умножив на dx обе части: o(x)dy + w(x)ydx = e(x)dx.
Исключив нулевые значения o(x), для оставшихся значений x записываем уравнение в разрешенном виде, поделив его на o(x).
Решение линейных дифференциальных уравнений
В данном классе уравнений есть два варианта. Первый — когда свободный член p(x) равен нулю (однородное), и второй — когда p(x) не равен нулю (неоднородное). Итак, у нас есть два следующих случая:
- y’ + r(x)y = 0 — однородное уравнение.
- y’ + r(x)y = p(x) — неоднородное уравнение.
Однородное легко приводится к разделенному виду y’/y = -r(x) или dy/y = -r(x)dx. После интегрирования получается общее решение для однородных уравнений: y = Ce -r(x) .
В общем случае линейное уравнение (неоднородное) решается в несколько этапов:
- Сначала решается соответствующее заданному уравнению однородно: p(x) условно приравнивается к 0. Положим, что u — это искомое решение, то есть мы имеем u’ + r(x)u = 0. Запомним это тождество.
- Введем в неоднородном уравнении замену y = uv, тогда (uv)’ + (uv)r(x) = p(x). Проведя некоторые преобразования, имеем v(r(x)u + u’) + uv’ = p(x). Вспоминая тождество из пункта 1, получаем v’u = p(x). В данном случае из v’ = p / u легко находится первообразная.
- В итоге решение неоднородного складывается из двух частей: u(C+V), в котором u — решение однородного с нулевой постоянной, а V — первообразная для соотношения p/u.
Еще одна путаница однородных уравнений возникает при рассмотрении однородных систем уравнений. Однако это другой вопрос, рассмотрение которого выходит за пределы данной статьи.
Примеры
Дана задача. Нужно найти решение.
| y’ + | ty | = | t |
| t 2 +1 | √(t 2 +1) |
Очевидно, данное уравнение неоднородно, поэтому решим сначала следующее уравнение:
| y’ + | ty | = 0 |
| t 2 +1 |
Следует отметить, что одним из решений уравнения является y = 0. Нахождение общего решения происходит через дифференциальную форму, которая позволяет воспользоваться разделением переменных:
| dy | = | (-1)tdt |
| y | t 2 +1 |
Интегрирование приводит к решению: ln|y| = A — ln(1+t 2 )/2. Представив A как ln B, можно записать решение более изящно:
| y | = | B |
| √(t 2 +1) |
Решение неоднородного уравнения выполним другим, аналогичным способом, который называется методом вариации постоянной, или метод Лагранжа. Опишем его теоретически.
Сделаем в дифференциальном уравнение вида r(x)y + y’ = p(x) замену y = c(x)e -R(x) , в котором R(x) — первообразная r(x), а с(x) — неизвестная функция, которую нужно определить.
После всех преобразований выясняется, что c'(x) = e R(x) f(x). Откуда с(x) легко находится интегрированием. Подставляя с(x) обратно в y = c(x)e -R(x) , получаем y = e -R(x) c(x) + De -R(x) — общее решение уравнения, где D — это постоянная, которая возникает при интегрирование c(x).
Применяя метод Лагранжа для нашей задачи, положим:
| y | = | c(t) |
| √(t 2 +1) |
Подставив эту замену в изначальное уравнение, найдем, что c(t) = (1/2)t 2 . Запишем решение неоднородного уравнения:
| y | = | x 2 | + | D |
| 2√(t 2 +1) | √(t 2 +1) |
Рассмотрим еще один пример. Найти решения (x — 2xy — y 2 )dy + y 2 dx = 0. Заметим, что y = 0 — одно из решений уравнения. Используя этот факт, мы можем поделить все части уравнения на выражение y 2 dy. После проведения некоторых преобразований получим:
| x’y | + | x(y)(1 — 2y) | = | 1 |
| y 2 |
Следует отметить, что мы словно бы развернули зависимость. Почему нет? x и y в функции являются равноправными и зависят друг от друга. Теперь у нас решается не функция y(x), а x(y), и x’y — это ничто иное, как производная функции x(y) по переменной y. Или dx/dy. В данном виде легко определить, что мы имеем дело с неоднородным уравнением, поэтому решаем данное однородное уравнение так:
| x’y | + | x(y)(1 — 2y) | = | 0 |
| y 2 |
Получаем x = Cy 2 e 1/y . Остается лишь найти вариационным методом решение изначального уравнения, положив x = y 2 c(y)e 1/y . После подстановки этой замены в уравнение, имеем:
| c'(y) | = | e -1/y |
| y 2 |
Откуда вычисляем, что c(y) = e -1/y + D. Решение задачи будет выглядеть следующим образом:
x = y 2 + Dy 2 e 1/y .
Мы рассмотрели способы решения линейных однородных уравнений.
Однородные дифференциальные уравнения
и приводящиеся к ним
Однородные уравнения
Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .
Например, функция есть однородная функция второго измерения, так как
При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как
Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:
Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .
Пример 1. Решить однородное уравнение .
Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим
Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .
Отсюда общее решение: .
При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.
Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.
Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.
Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.
Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).
Уравнения, приводящиеся к однородным
А. Рассмотрим дифференциальное уравнение вида
где — постоянные, а — непрерывная функция своего аргумента .
Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.
Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.
1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду
Выбирая и как решение системы линейных уравнений
получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).
2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.
Пример 3. Решить уравнение .
Решение. Рассмотрим систему линейных алгебраических уравнений
Определитель этой системы .
Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид
Это уравнение является однородным уравнением. Полагая , получаем
Интегрируя, найдем или .
Возвращаемся к переменным :
Пример 4. Решить уравнение .
Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид
Разделяя переменные, получаем
Возвращаясь к переменным , получаем общий интеграл данного уравнения
Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .
Пример 5. Решить уравнение .
Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим
Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .
Положим ; исходное уравнение принимает вид
Положим теперь . Тогда это уравнение примет вид , откуда .
Разделяем переменные в этом уравнении . Интегрируя, найдем
Заменяя через , получаем общий интеграл данного уравнения
Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.
Однородные дифференциальные уравнения
Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными заменой y = xu, или, что тоже самое, 
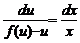
Пример. Решить уравнение (y 2 — 2xy)dx + x 2 dy = 0. Это однородное уравнение, так как y 2 — 2xy и x 2 однородные функции второй степени. Делаем замену y = xu, dy = udx + xdu. Подставляя в уравнение, имеем
(x 2 u 2 — 2x 2 u)dx + x 2 (udx + xdu) = 0.
Раскрывая скобки, приводя подобные и сокращая на x 2 , получаем уравнение с разделяющимися переменными
(u 2 — u)dx + xdu = 0
Разделяя переменные, получаем 



Уравнения вида 

Решить однородные уравнения онлайн можно с помощью специального сервиса Дифференциальные уравнения онлайн.
http://mathhelpplanet.com/static.php?p=odnorodnye-differentsialnye-uravneniya
http://math.semestr.ru/math/lec_diffur_3.php