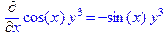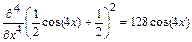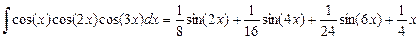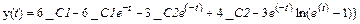Запись дифференциальных уравнений в maple
Общее решение дифференциальных уравнений.
Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact . При составлении дифференциальных уравнений для обозначения производной применяется команда diff , например, дифференциальное уравнение y» + y = x записывается в виде: diff(y(x),x$2)+y(x)=x.
Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _ С1 , _ С2 , и т.д.
Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).
Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%) .
Задание 1.1.
1. Найти общее решение дифференциального уравнения y ‘+ y cos x =sin x cos x .
de : =

Итак, решение искомого уравнения есть функция 
Замечание : при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _ С1 .
2. Найти общее решение дифференциального уравнения второго порядка y » — 2 y ‘+ y =sin x + e — x .
deq :=
Замечание : так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _ С1 и _ С2 . Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.
3. Найти общее решение дифференциального уравнения порядка y »+ k 2 y =sin( qx ) в двух случаях: q ¹ k и q = k (резонанс).
de :=
Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q = k .
Замечание : в обоих случаях частное решение неоднородного уравнения и общее решение, содержащее произвольные постоянные, выводятся отдельными слагаемыми.
Фундаментальная (базисная) система решений.
Команда dsolve представляет возможность найти фундаментальную систему решений (базисные функции) дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis .
Задание 1.2.
Найти фундаментальную систему решений дифференциального уравнения: y (4) +2 y »+ y =0.
de : =
> dsolve(de, y(x), output=basis);
Решение задачи Коши или краевой задачи.
Команда dsolve может найти решение задачи Коши или краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор 



Задание 1.3.
1. Найти решение задачи Коши: y (4) + y »=2cos x , y (0)= — 2, y ‘(0)=1, y »(0)=0, y »'(0)=0.
cond:= y(0)= — 2, D(y)(0)=1, (D (2) )(y)(0)=0, (D (3) )(y)(0)=0
y( x )= — 2cos( x ) — x sin( x )+ х
2. Найти решение краевой задачи: 


de : =
y( x )=2 x — p + p cos( x )
Замечание : для построения графика решения предварительно следует отделить правую часть полученного выражения.
Системы дифференциальных уравнений.
Команда dsolve может найти решение системы дифференциальных уравнений (или задачи Коши), если в ней указать: dsolve(
Задание 1.4.
Найти решение системы дифференциальных уравнений:
Найдены две функции x ( t ) и y ( t ), которые зависят от двух произвольных постоянных _ С1 и _ С2 .
Приближенное решение дифференциальных уравнений с помощью степенных рядов.
Для многих типов дифференциальных уравнений не может быть найдено точное аналитическое решение. В этом случае дифференциальное уравнение можно решить с помощью приближенных методов, и, в частности, с помощью разложения в степенной ряд неизвестной функции.
Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series ). Для того, чтобы указать порядок разложения n , т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n .
Если ищется общее решение дифференциального уравнения в виде разложения в степенной ряд, то коэффициенты при степенях х найденного разложения будут содержать неизвестные значения функции в нуле y(0) и ее производных D(y)(0), (D@@2)(y)(0) и т.д. Полученное в строке вывода выражение будет иметь вид, похожий на разложение искомого решения в ряд Маклорена, но с другими коэффициентами при степенях х . Для выделения частного решения следует задать начальные условия y(0)=у1, D(y)(0)=у2, (D@@2)(y)(0)=у3 и т.д., причем количество этих начальных условий должно совпадать с порядком соответствующего дифференциального уравнения.
Разложение в степенной ряд имеет тип series , поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom) , а затем выделить правую часть полученного выражения командой rhs(%) .
Задание 1.5.
1. Найти решение задачи Коши: 

y(0)=0>, y(x), type=series);
В полученном решении слагаемое 
2. Найти общее решение дифференциального уравнения y »( х ) — y 3 ( х )= е — х cos x , в виде разложения в степенной ряд до 4-го порядка. Найти разложение при начальных условиях: y (0)=1, y ‘(0)=0.
> restart; Order:=4: de:=diff(y(x),x$2)-
Замечание : в полученном разложении запись D(y)(0) обозначает производную в нуле: y ‘(0). Для нахождения частого решения осталось задать начальные условия:
3. Найти приближенное решение в виде степенного ряда до 6-го порядка и точное решение задачи Коши: 



de : =
cond :=y(0)=1, D(y)(0)=1, D (2) (y)(0)=1
y( x )=
y( x )=
Замечание : тип решения дифференциального уравнения в виде ряда есть series , поэтому для дальнейшего использования такого решения (вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert
На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале — 1 x
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Дифференциальные уравнения
ЛАБОРАТОРНАЯ РАБОТА № 7
СИСТЕМА КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MAPLE.
ОПЕРАЦИИ И ФУНКЦИИ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Цель работы:приобрести практические навыки решения некоторых задач математического анализасредствамиСКМ Maple.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Дифференцирование
Вычисление производных функции 
diff (a, x1, x2,…, xn), diff(a, [x1, x2, … , xn]),
Diff (a, x1, x2,…, xn), Diff(a, [x1, x2, …, xn]).
Здесь а– дифференцируемое алгебраическое выражение, в частности функция f(x1, x2,…,xn)ряда переменных, по которым производится дифференцирование.
В простейшей форме diff(f(x),x)вычисляет первую производную функции f(x)по переменной x. При n, большем 1, вычисления производных выполняются рекурсивно, например, Diff(diff(f(x),x),y. Или же для вычисления производных высокого порядка можно использовать оператор x$n, где n– порядок производной.Например,выражениеdiff(f(x),x$4),вычисляющее производную четвертого порядка по x,эквивалентно по записи diff(f(x),x,x,x,x).
После выполнения дифференцирования полученное выражение желательно упростить. Для этого следует использовать команды simplify factor или expand, в зависимости от того, в каком виде нужен результат.
Для вычисления производных в заданной точке можно использовать дифференциальный оператор, для определения которого используется команда D(f), где f – функция.
Интегрирование
Вычисление неопределенного интеграла 
int(f, x), int(f, x=a..b),
int(f, x = a..b, continuous);
Int(f, x), Int(f, x=a..b),
Int(f, x=a..b, continuous).
Здесь f – подынтегральная функция,
x – переменная, по которой выполняются вычисления,
аиb –верхний и нижний пределы интегрирования,
continuous – необязательное дополнительное условие. Если в команде интегрирования добавить эту опцию, то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций.
Для вычисления определенного интеграла необходимо использовать функцию evalf(int(f, x=a..b),е), где e – точность вычислений (число значащих цифр результата).
Если верхним пределом интегрирования является бесконечность, то она обозначается словом infinity.
Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо других ограничений. Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.
После наложения ограничений на параметр Maple добавляет к его имени символ (
), например, параметр a, на который были наложены некоторые ограничения, в сроке вывода будет иметь вид: a
Описание наложенных ограничений параметра a можно вызвать командой about(a).
Дифференциальные уравнения
Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y»+y=x записывается в виде diff(y(x),x$2)+y(x)=x.
Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.
Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения), следует отделить правую часть полученного решения командойrhs(%).
Если, помимо дифференциального уравнения, задать начальные или краевые условия для неизвестной функции, команда dsolve может найти решение задачи Коши или краевой задачи Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор 

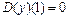
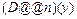
Команда dsolve может найти решение системы дифференциальных уравнений (или задачи Коши), если в ней указать: dsolve(
Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет графического представления решений дифференциальных уравнений Detools.
Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда сама производит численное решение дифференциального уравнения. Формат этой команды: DEplot: DEplot(de, vars, range, x=х1..х2, y=у1..у2, cond, ptions), где de — дифференциальное уравнение или система дифференциальных уравнений; vars– список неизвестных функций; range – диапазон измерения независимой переменной; cond – начальные условия; x=х1..х2 и y=у1..у2– диапазоны изменения функций; options– дополнительные параметры.
Наиболее часто используемые параметры: linecolor=цвет линии; scene=[x,y]- определяет, какие зависимости выводить на график; iterations=число итераций, необходимое для повышения точности вычислений (по умолчанию это число равно 1); stepsize=число, равное расстоянию между точками на графике, по умолчанию оно равно (x2-x1)/20, этот параметр необходим для вывода более гладкой кривой решения; obsrange=true/false — прерывать или нет вычисления, если график решения выходит за установленный для рисования интервал.
Для решения дифференциального уравнения n-ого порядка начальные условия можно задавать в более компактной форме: [x0, y0, y’0, y»0,…], где x0- точка, в которой задаются начальные условия; y0- значение искомой функции в точке x0; y’0, y»0,… — значения производных первой, второй и т.д. до (n-1)-ого порядка.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1.Найти производные указанных порядков:
f ’ (x)=ax n , f’(x)= sin(x), f’(x,y)= cos(x)y 3 , f”(x,y)= cos(x)y 3 ,f””(x)=cos(2x) 2 .
Полученное выражение можно упростить двумя способами:
Задание 2. Вычислить вторую производную функции f(x)=sin 2 (x)/(2+sin(x)) в точках x=p/2, x=p.
х:=
Задание 3.Найти значения определенных интегралов
а) 

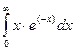
>Int(x*exp(-x),x=0..infinity) = evalf(int(x*exp(-x), x=0..infinity),1);
Задание 4.Найти неопределенные интегралы:
а) 

Задание 5. Найти определенный интеграл
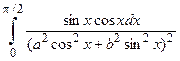
> assume (a>0); assume (b>0);
и несобственный интеграл 
>Int((1-exp(-a*x^2))/(x*exp(x^2)),x=0..+infinity) =int((1-exp(-a*x^2))/(x*exp(x^2)), x=0..+infinity);
Задание 6.Найти общее решение дифференциального уравнения y‘+ycosx=sinxcosx.
de:=

Задание 7. Найти общее решение дифференциального уравнения второго порядка y»-2y‘+y=sinx+e — x .
deq:=
Задание 8. Найти решение задачи Коши:
Задание 9. Найти решение краевой задачи:



de:=
Замечание: для построения графика решения предварительно следует отделить правую часть полученного выражения.
Задание 10. Найти решение системы дифференциальных уравнений:
Найдены две функции x(t) и y(t), которые зависят от двух произвольных постоянных _С1 и _С2.
Задание 11. Нарисовать график решения дифференциального уравнения:

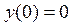
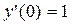
в интервале 
(D@@2)(y)(0)=1]], stepsize=.1, linecolor=black,
Задания для самостоятельной работы
Задание 1. Найти значение первой и второй производных функции f(x).
| Вари-ант | Условие | Вари-ант | Условие |
а)  ; б) ; б)  . . | а)  ; б) ; б)  . . | ||
а)  ; б) ; б) 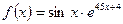 . . | а)  ; б) ; б)  . . | ||
а) 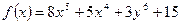 ; б) ; б)  . . | а)  ; б) ; б)  . . | ||
а)  ; б) ; б)  . . | а)  ; б) ; б)  . . | ||
а)  ; б) ; б) 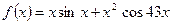 . . | а) 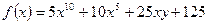 ; б) ; б) 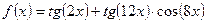 . . |
Задание 2. Найти значение определенного интеграла, дать графическую интерпретацию решения.
| Вариант | Условие | Вариант | Условие |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
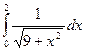 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  |
Задание 3. Решить дифференциальное уравнение и систему дифференциальных уравнений. Проиллюстрировать решение графически.
Запись дифференциальных уравнений в maple
Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y»+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.
Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.
Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).
Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).
1. Найти общее решение дифференциального уравнения y’+ycosx=sinxcosx.
Итак, решение искомого уравнения есть функция
Замечание: при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _С1.
Найти общее решение дифференциального уравнения второго порядка y» — 2y’+y=sinx+e — x.
Замечание: так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _С1 и _С2. Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.
3. Найти общее решение дифференциального уравнения порядка y»+k2y=sin(qx) в двух случаях: q ¹ k и q=k (резонанс).
Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q=k.
Фундаментальная (базисная) система решений.
Команда dsolveпредставляет возможность найти фундаментальную систему решений (базисные функции) дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis.
Найти фундаментальную систему решений дифференциального уравнения: y(4)+2y»+y=0.
>dsolve(de, y(x), output=basis);
Решение задачи Коши или краевой задачи.
Команда dsolve может найти решение задачи Коши или краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор , например, условие y»(0)=2 следует записать в виде
1. Найти решение задачи Коши: y(4)+y»=2cosx, y(0)= — 2, y'(0)=1, y»(0)=0, y»'(0)=0.
y(x)= — 2cos(x) — xsin(x)+ х
2. Найти решение краевой задачи:кккк
y(x)=2x — p + p cos(x)
Замечание: для построения графика решения предварительно следует отделить правую часть полученного выражения.
Системы дифференциальных уравнений.
Команда dsolve может найти решение системы дифференциальных уравнений (или задачи Коши), если в ней указать: dsolve(
Найти решение системы дифференциальных уравнений:
Найдены две функции x(t) и y(t), которые зависят от двух произвольных постоянных _С1 и _С2.
Приближенное решение дифференциальных уравнений с помощью степенных рядов.
Для многих типов дифференциальных уравнений не может быть найдено точное аналитическое решение. В этом случае дифференциальное уравнение можно решить с помощью приближенных методов, и, в частности, с помощью разложения в степенной ряд неизвестной функции.
Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series). Для того, чтобы указать порядок разложения n, т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n.
Если ищется общее решение дифференциального уравнения в виде разложения в степенной ряд, то коэффициенты при степенях х найденного разложения будут содержать неизвестные значения функции в нуле y(0) и ее производных D(y)(0), (D@@2)(y)(0) и т.д. Полученное в строке вывода выражение будет иметь вид, похожий на разложение искомого решения в ряд Маклорена, но с другими коэффициентами при степенях х. Для выделения частного решения следует задать начальные условия y(0)=у1, D(y)(0)=у2, (D@@2)(y)(0)=у3 и т.д., причем количество этих начальных условий должно совпадать с порядком соответствующего дифференциального уравнения.
Разложение в степенной ряд имеет тип series, поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom), а затем выделить правую часть полученного выражения командой rhs(%).
1. Найти решение задачи Коши:
y(0)=0>, y(x), type=series);
В полученном решении слагаемое O(x^5) означает, что точность разложения была до 5-го порядка.
2. Найти общее решение дифференциального уравнения y»(х) — y3(х)=е — хcosx, в виде разложения в степенной ряд до 4-го порядка. Найти разложение при начальных условиях: y(0)=1, y'(0)=0.
>restart; Order:=4: de:=diff(y(x),x$2)-
Замечание: в полученном разложении запись D(y)(0) обозначает производную в нуле: y'(0). Для нахождения частого решения осталось задать начальные условия:
3. Найти приближенное решение в виде степенного ряда до 6-го порядка и точное решение задачи Коши:
Замечание: тип решения дифференциального уравнения в виде ряда есть series, поэтому для дальнейшего использования такого решения (вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert
На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале — 1
Численное решение дифференциальных уравнений
Численное решение дифференциальных уравнений с помощью команды dsolve. Построение графиков решений дифференциальных уравнений с помощью команды odeplot.
Для того, чтобы найти численное решение дифференциального уравнения (задачи Коши или краевой задачи) в команде dsolve следует указать параметр type=numeric (или просто numeric). Тогда команда решения дифференциального уравнения будет иметь вид dsolve(eq, vars, type=numeric, options), где eq – уравнения, vars – список неизвестных функций, options – параметры, позволяющие указать метод численного интегрирования дифференциального уравнения. В Maple реализованы такие методы: method=rkf45 — метод Рунге-Кутта-Фельберга 4-5-ого порядка (установлен по умолчанию); method=dverk78 – метод Рунге-Кутта 7-8 порядка; mtthod=classical – классический метод Рунге-Кутта 3-его порядка; method=gear и method=mgear – одношаговый и многошаговый методы Гира.
График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x,y(x)], x=x1..x2), где в качестве функции используется команда dd:=dsolve(
1. Найти численное и приближенное решение в виде степенного ряда до 6-ого порядка задачи Коши: ,
Сначала найдем численное решение задачи Коши
Замечание: в строке вывода появляется сообщение о том, что при решении использован метод rkf45. Во избежание вывода строк, не несущих полезной информации, рекомендуется отделять промежуточные команды двоеточием. Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х=0.5, то следует набрать:
Теперь найдем приближенное решение задачи Коши в виде степенного ряда и построим графики численного решения и полученного степенного ряда в интервале их наилучшего совпадения.
Наилучшее приближение решения степенным рядом достигается примерно на интервале — 1
2. Построить графики решений задачи Коши системы дифференциальных уравнений:
х ‘(t)=2y(t)sin(t) — х (t) — t,
Пакет графического представления решений дифференциальных уравнений Detools.
Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools.
Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда аналогична команде odeplot, но более функциональна. Она, в отличие от odeplot, сама производит численное решение дифференциального уравнения. Основные параметры DEplot похожи на параметры odeplot: DEplot(de, vars, range, x=х1..х2, y=у1..у2, cond, ptions), где de — дифференциальное уравнение или система дифференциальных уравнений; vars – список неизвестных функций; range – диапазон измерения независимой переменной; cond – начальные условия; x=х1..х2 и y=у1..у2 – диапазоны изменения функций; options – дополнительные параметры.
Наиболее часто используемые параметры: linecolor=цвет линии; scene=[x,y] — определяет, какие зависимости выводить на график; iterations=число итераций, необходимое для повышения точности вычислений (по умолчанию это число равно 1); stepsize=число, равное расстоянию между точками на графике, по умолчанию оно равно (x2 — x1)/20, этот параметр необходим для вывода более гладкой кривой решения;obsrange=true/false — прерывать или нет вычисления, если график решения выходит за установленный для рисования интервал.
Для решения дифференциального уравнения n-ого порядка начальные условия можно задавать в более компактной форме: [x0, y0, y’0, y»0,…], где x0 — точка, в которой задаются начальные условия, y0 — значение искомой функции в точке x0, y’0, y»0,… — значения производных первой, второй и т.д. до (n — 1)-ого порядка.
Нарисовать график решения дифференциального уравнения:
, у(0)=0,у'(0)=1 ,у»(0)=1 , в интервале .
> restart; with(D Е tools):
(D@@2)(y)(0)=1]], stepsize=.1, linecolor=black,
Построение фазовых портретов систем дифференциальных уравнений.
Для дифференциального уравнения порядка выше первого команда DEplot рисует только кривые решений дифференциальных уравнений, а для систем дифференциальных уравнений первого порядка могут быть нарисованы и фазовые портреты.
С помощью команды DEplot можно построить фазовый портрет в плоскости (x, y), для системы двух дифференциальных уравнений:
Если система дифференциальных уравнений является автономной, то на фазовом портрете будет построено поле направлений в виде стрелок. Размер стрелок регулируется параметром arrows=SMALL, MEDIUM, LARGE, LINE или NONE.
Для того, чтобы нарисовать весь фазовый портрет, необходимо для каждой фазовой траектории указывать начальные условия: например, для системы двух дифференциальных уравнений первого порядка несколько начальных условий в команде DEplots указываются после задания диапазона изменения независимой переменной t: [[x(0)=x1, y(0)=y1], [x(0)=x2, y(0)=y2],…, [x(0)=xn, y(0)=yn]].
Начальные условия можно задавать в более компактной форме: [t0, x0, y0], где t0 — точка, в которой задаются начальные условия, x0 и y0 — значения искомых функций в точке t0.
Фазовый протрет системы двух дифференциальных уравнений первого порядка можно также построить с помощью команды phaseportrait(sys, [x,y],x1..x2,[[cond]]), где sys — система двух дифференциальных уравнений первого порядка, [x,y] — имена искомых функций, x1..x2 — интервал, на котором следует построить фазовый портрет, а в фигурных скобках указываются начальные условия. Эта команда находится в пакете DEtools, поэтому данный пакет должен быть предварительно загружен.
1. Построить фазовый портрет системы дифференциальных уравнений:
для нескольких наборов начальных условий: х(0)=1, у(0)=0.2; х(0)=0, у(0)=1; х(0)=1, у(0)=0.4; х(0)=1, у(0)=0.75; х(0)=0, у(0)=1.5; х(0)= — 0.1, у(0)=0.7.
> restart; with(D Е tools):
stepsize=0.1, arrows=none, linecolor=black);
2. Построить фазовый портрет с полем направлений автономной системы
для различных начальных условий х(0)=1, у(0)=0; х(0)= — 1, у(0)=0; х(0)= p , у(0)=1; х(0)= — p , у(0)=1; х(0)=3 p , у(0)=0.2; х(0)=3 p , у(0)=1; х(0)=3 p , у(0)=1.8; х(0)= — 2 p , у(0)=1;.
> restart; with(D Е tools):
3. Построить фазовый портрет системы дифференциальных уравнений:
Начальные условия, диапазон изменения переменной и размеры координатных осей подбираются самостоятельно из соображений наглядности фазового портрета.
http://lektsii.org/6-64849.html
http://www.sites.google.com/site/camoucitelmaple13/urok-7-analiticeskoe-resenie-differencialnyh-uravnenij-cislennoe-resenie-differencialnyh-uravnenij