Записать функцию и уравнение лагранжа

Функция Лагранжа

Назначение сервиса . Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:

1. составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений g_i(x);
2. находятся частные производные функции Лагранжа, ∂L/∂x_i, ∂L/∂λ_i;
3. составляется система из (n + m) уравнений, ∂L/∂x_i = 0.
4. определяются переменные x_i и множители Лагранжа λ_i.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.

Правило множителей Лагранжа

Пример 1 . Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x₁ 2 + x₂ 2
h₁(x) = 2x₁ + x₂ -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x₁ 2 + x₂ 2 + λ(2x₁ + x₂ – 2) → min
Решение:

Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,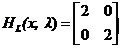
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x * = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ * и x₂ * в уравнение ограничений 2x₁ + x₂ -2 = 0, откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x * с координатами x₁ * = 0.8 и x₂ * = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x * = [0.8; 0.4] T , f(x * ) = 0.8

Пример 2 . Исследовать на условный экстремум функцию f(x,y)_max = x 2 + 8xy+3y 2 при данных уравнениях связи.
9x +10y = 29

Теоретическая механика. Уравнения Лагранжа

В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.

Итак, типовое задание выглядит так.

Прежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение — переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.

Итак, приступим к решению.

Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:

Расчет начинаем с записи уравнений связи — выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто

С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует

Самое трудное — выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная — это скорость поступательного движения призмы 3. Относительное — скольжение вдоль паза 2, которое описано координатой S. Значит

Векторно складываем эти две скорости

Второе выражение здесь — это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так.

Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.

Шарик 1 обладает энергией

Призма 3 движется поступательно

Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений

Полная кинетическая энергия системы

Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.

Сначала по координате x. Частные производные

Производную по x с точкой дифференцируем по времени

Теперь то же самое по координате S. Частные производные

Производная по времени

Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так

На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.

Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так

Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем

Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.

Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).

Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.

1) Определить число степеней свободы и выбрать обобщенные координаты

2) Записать уравнения связей

3) Записать выражение для кинетической энергии

4) Взять необходимые производные

5) Записать обобщенные силы по каждой координате

6) Записать уравнения Лагранжа

Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.

Функция Лагранжа

Содержание:

Теория производных функций Лагранжа

В XVIII в. были сделаны также попытки обоснования анализа с помощью средств, которые представлялись чисто алгебраическими» Здесь следует прежде всего назвать английского математика-самоучку Джо-лана Ландена (1719—1790), имя которого носит одно важное преобразование в теории эллиптических интегралов.

Свои взгляды Ланден изложил в книге «Рассуждение о разностном анализе: новая ветвь алгебраического искусства» (Л discourse concerning residual analysis: a new branch of algebraic art. London, 1758).

Понятию производной у Ландена соответствует «специальное значение» частного —- при для которого он ввел особый знак; так, в случае специальным значением частного является Для степенной функции где — целые числа, Ланден доказывал формулу 1

положив он вывел таким образом производную степенной функции с рациональным показателем. Он пытался обобщить свой вывод и на иррациональные показатели, беря для примера показатель рассматриваемыи как «последнее значение» своих десятичных приближений 1, и т. д.

Отыскание же производной любой функции сводилось в принципе к почленному дифференцированию степенного ряда, поскольку «заранее предполагалось, что разность разлагается по степеням разности По существу Ланден доопределял функцию

По этой ссылке вы найдёте полный курс лекций по высшей математике:

для значения по непрерывности, подобно Ньютону и Эйлеру,— еще Лакруа в своем «Трактате» указывал, что разностный анализ сводится к методу пределов.

Лагранж, который развил собственную алгебраическую концепцию анализа несколько позднее, писал, что Ландену действительно удалось избежать бесконечно малых и исчезающих количеств, но характеризовал приемы и применения разностного анализа как «затруднительные и мало естественные»

Центральную мысль своей теории производных функций Лагранж впервые высказал в мемуаре «О новом роде исчисления, относящегося к дифференцированию и интегрированию переменных величин» (Sur une nou-velle espece du calcul relatif a la differentiation et a l’integration des quan-tites variables. Nouv. Mem. Ac. Berlin, (1772) 1774). Эта мысль заключается в следующем: при записи разложения функции от по степеням в форме

функции последовательно получаются одна из другой, начиная с по одному и тому же правилу: каждая из них есть коэффициент при первой степени в разложении по степеням ей предшествующей.

Возможно вам будут полезны данные страницы:

Таким образом, все эти функции могут быть произведены (derivees) из начальной с помощью повторного применения операции разложения в степенной ряд — операции, которую Лагранж считал чисто алгебраической.

Функкции

Функции

Лагранж назвал производными от начальной;

обозначения и т. п., без скобок, он применил еще

ранее в одной статье, напечатанной в «Miscellanea Taurinensia», 1760—1761. Мы отмечали ранее, что еще Эйлер в 1755 г. особенно подчеркивал возможность нахождения производной из разложения в степенной ряд (см. стр. 2(>9).

Лагранж положил эту идею в самое основание анализа. Развернутое построение системы анализа на этой основе Лагранж дал только четверть века спустя, но еще до того два математика, вероятно, вдохновляемые мемуаром Лагранжа 1772 г., развили, каждый по-своему, начала такого построения. Первым из них был Кондорсе, который в 1778—1782 гг. готовил энциклопедический курс анализа под названием «Трактат по интегральному исчислению» (Traite du calcul integral), оставшийся незаконченным.

Рукопись и некоторое число уже набранных ее листов хранятся в библиотеке Национального института в Париже. К ним приложена записка Лакруа, где, между прочим, сказано: «Изложение начал дифференциального исчисления, полностью содержащееся в отпечатанных листах, будучи независимым от какого-либо понятия о бесконечно малых и о пределах, показалось бы новым в случае публикации, ибо тогда по этому вопросу был известен только мемуар Лагранжа, помещенный в томе Берлинской академии за 1772 г.» Ч Наряду с этим Лакруа отмечал большую сложность вычислений Кондорсе в сравнении с изложением в позднейших трудах Лагранжа.

Мы можем ограничиться указанием, что Кондорсе вводил последовательные производные точно так же, как Лагранж (ср. стр. 288), и что он один из первых, если не первый, стал употреблять термин «аналитическая функция».

Другим единомышленником Лагранжа явился Франсуа Луи Антуан Арбогаст (1759—1803), воспитанник университета в Страсбурге, профессор математики в различных учебных заведениях Эльзаса, член Института, т. е. Академии наук в Париже, и в 1793—1795 гг. депутат Национального конвента, активно участвовавший в реформе народного образования.

В апреле 1789 г. Арбогаст представил Парижской академии «Опыт о новых началах дифференциального и интегрального исчисления, независимых от теорий бесконечно малых и пределов» (Essai sur les nouvcaux prin-cipes du calcul dilferentiel et de calcul integral, independants de la theorie des infiniment petits et de celle de limites).

Работа была передана на заключение Лежандру и Лагранжу, которые представили свой отзыв в мае. Отзыв, по-видимому, пропал, а рукопись не увидела света и хранится в настоящее время во Флоренции 2. Сжатое изложение принципов этого труда, публикации которого помешали перерыв в 1790 г. издания ученых записок Парижской академии, затем бурные политические события того времени и, наконец, выход в 1797 г. «Теории аналитических функций»

• Лагранжа, Арбогаст дал в предисловии к своей книге «Об исчислении дериваций» (Du calcul des derivations. Strasbourg, an VIII 1 (1800).

«Опыт» Арбогаста состоит из двух отделов. В первом определяются дифференциалы различных порядков через коэффициенты ряда Тейлора, а самый ряд выводится при двух предположениях: 1) что произвольная функция у представима обобщенным степенным рядом

где — любые действительные числа, и 2) что биномиальное разложение справедливо для всех действительных показателей. Арбогаст записывает приращенное значение функции

в виде ряда по степеням где обозначают соответственно величипы и т. п. Обозначив выражения в фигурных скобках, после первого, равного через Арбогаст получает

и констатирует, что коэффициенты последнего ряда, начиная второй степени, последовательно умноженные на 1.2, 1.2.3, . «производятся одни из других таким же способом и следуя тому же приему, как коэффициент при производится из функции Выражения

Арбогаст называет первым, вторым, третьим, . дифференциалами функции и затем применяет общеупотребительную символику. Далее Арбогаст утверждает, что при достаточно малом приращении ряд Тейлора сходится, а каждый член его оказывается (по абсолютной величине) большим (абсолютной величины) суммы всех следующих за ним членов. На этой основе выведены главные правила дифференцирования функций одного переменного и приемы отыскания экстремумов.

Во втором отделе содержатся начала теории соприкосновения плоских кривых и вычислены дифференциалы площади и длины дуги кривой в прямоугольных координатах.

Лагранж высоко оценил работу Арбогаста и во введении к первому изданию «Теории аналитических функций» (1797), упомянув о своем мемуаре 1772 г., писал, что позднее Арбогаст представил Академии наук «прекрасный мемуар, в котором та же мысль изложена с принадлежащими ему развитиями и приложениями.

Это сочинение не оставляет ничего пожелать в вопросе, о ко по ром идет речь» Во втором издании той же книги (1813) приведенные курсивом слова отсутствуют . И. Ю. Тимченко по этому поводу заметил, что «Лагранж, очевидно, принимал слишком близко к сердцу вопрос о приоритете теории аналитических функцию) Впрочем, приоритет действительно принадлежал Лагранжу.

Полное название не раз цитированного труда Лагранжа выражает его основную установку: «Теория аналитических функций, содержащая начала дифференциального исчисления, освобожденные от всякого рассмотрения бесконечно малых, исчезающих, пределов и флюксий и сведенные к алгебраическому анализу конечных величин» (Theorie des fonctions апа-jytiques contenant les principes du calcnl differentiel, degages de toute consideration d’infiniment petits, d’evanouissants, de limites et de fluxions, et reduits a Tanalyse algebrique des quantites finies. Paris, 1797; 2-е пересмотренное и дополненное издание. Париж, 1813).

Книга возникла в связи с тем, что Лагранж стал читать курс анализа в Политехнической школе; к ней очень близки «Лекции об исчислении функций» (Lemons sur le calcul des fonctions), напечатанные сперва в «Seances de l’Ecole normale», an IX (1801); второе значительно дополненное издание вышло в Париже в 1806 г.

«Теория аналитических функций» заключает, помимо введения, три части: 1) изложение теории и ее главных применений в анализе; 2) приложения к геометрии, 3) приложения к механике, причем во всей книге нет ни одного чертежа, как, впрочем, и в «Аналитической механике» Лагранжа. Введение к книге содержит сжатый историко-критический очерк существовавших в XVIII в. методов обоснования анализа.

Дифференциальное и интегральное исчисление Лейбница Лагранж по-прежнему считал исчислением компенсирующихся ошибок; задачу общего доказательства неизбежности такой компенсации он считал нерешенной и после выхода в свет первого издания «Размышлений» (1797) Карно. В методе пределов Лагранж усматривал тот же недостаток, что и в концепции Эйлера: в обоих случаях дело приводится к рассмотрению отношений между нулями, а такое отношение перестает быть для разума ясной и точной идеей.

Этим и другим методам он противопоставлял теорию аналитических функций. Необходимо, однако, напомнить, что в этот термин Лагранж вкладывлл смысл, несколько отличный от современного. В «Рассуждении о предмете теории аналитических функций» (Discours sur l’objet de la theorie des lonclions analytiques. Journal de l’Ecole Polytechnique, an VII (1799) он разделяет все учение о функциях на две ветви. К первой относится алгебра, где изучаются лишь первоначальные функции, происходящие в результате алгебраических действий над переменными и числами. Вторая ветвь — это теория аналитических функций, в которой рассматриваются не только первоначальные функции, возникающие при любых вычислениях (Лагранж иногда называл функции expressions de calcul), но и их производные функции.

Начала своей теории Лагранж закладывает в первых двух главах труда, о котором идет речь. Он прежде всего желает обосновать постоянно обнаруживаемый в практике вычислений факт, что любая функция при подстановке вместо раскладывается в ряд вида

Сперва доказывается, что разложение не может содержать дробных положительных степеней за исключением отдельных особых значений Радикалы, содержащие рассуждает Лагранж, могут произойти только от радикалов, имеющихся в первоначальной функции Но в таком случае допущение членов вида приводит к нелепости: ряд в котором все возможные значения комбинируются с каждым из значений радикала дает для

больше различных значений, чем их имеет между тем, если остаются неопределенными, то число этих значений в обоих случаях должно быть одинаково. Лишь при отдельных определенных значениях некоторые радикалы в могут уничтожиться, сохраняясь в Подобного рода исключительные случаи рассмотрены в главе 1.

Затем Лагранж показывает, что разложение функции не может, вообще говоря, содержать отрицательные степени член вида при стал бы бесконечным и, значит, должна была бы стать бесконечной при неопределенном функция между тем как это может случиться только при особых значениях

Подчеркнем еще раз, что Лагранж, как и все математики XVIII в., заранее принимал, что любая функция анализа представима рядом по ка-ким-либо действительным степеням и в доказательстве, с его точки зрения, нуждалось только предложение, что такой ряд, вообще говоря, содержит лишь целые положительные степени, между тем как другие степени встречаются исключительно в разложениях, соответствующих изолированным особым значениям аргумента. В V главе «Теории аналитических

функций он писал, что «разложение и т. д. может стать ошибочным для какого-либо данного значения лишь в случае, если для этого значения станет бесконечной одна из функций и т. д., так же как и все следующие. Тогда, если есть индекс первой ставшей бесконечной функции, разложение, о котором идет речь, должно будет содержать член вида где — число, заключенное между А если становятся бесконечными для одного и того же значения все функции и т. д., то разложение содержит в этом случае отрицательные степени Более подробно последний случай Лагранж рассмотрел в VIII главе «Лекций об исчислении функций».

Однако приведенные выше рассуждения Лагранжа опирались не только на допущение о представимости произвольной функции обобщенным степенным рядом, но и на уверенность в том, что выведенные посредством формальных алгебраических преобразований ряды представляют соответствующие функции, вообще говоря, повсюду, так что свойства, принадлежащие при каких-либо значениях ряду, принадлежат и функции.

Между тем Коши показал, что сходящийся ряд Тейлора не обязательно сходится к порождающей его функции, и тем самым выявил принципиальную недостаточность теории Лагранжа (см. стр. 300).

Установив общий вид степенного ряда, выражающего данную функцию, Лагранж переходит к рассмотрению его членов. Так как разность равна нулю при то она может быть представлена в виде произведения целой положительной степени на некоторую функцию конечную при Таким образом, можно положить

Если функция при обращается в то аналогично где обращается в при при сходных обозначениях далее получается, что и т. д., так что

и в итоге для разложения получается тот ряд, какой был предположен вначале.

Описанный прием может быть употреблен для непосредственного разложения рациональных функций, а также иррациональных алгебраических функций, что Лагранж иллюстрирует на примерах и Коэффициенты разложения выступают при этом вычислении как «специальные значения» Ландена (стр. 282). Так, коэффициент есть значение при функции или же равного ей выражения в котором деление на уже произведено.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.