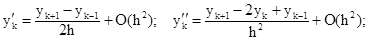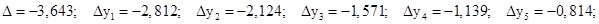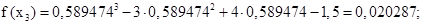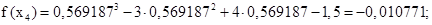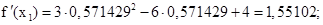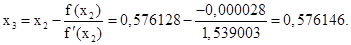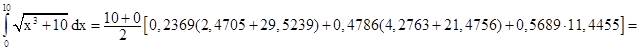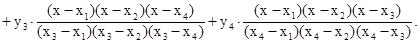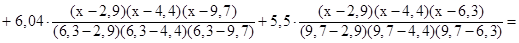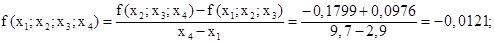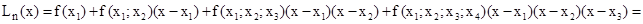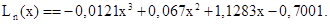Конечно-разностный метод решения краевых задач.
для обыкновенных дифференциальных уравнений.
Примером краевой задачи является двухточечная краевая задача для обыкновенного дифференциального уравнения второго порядка:
с граничными условиями, заданными на концах отрезка [a; b]:
Следует найти такое решение у(х) на этом отрезке, которое принимает на концах отрезка значения у0, у1. Если функция 
линейна по аргументам 
, то задача поиска этой функции – линейная краевая задача, в противном случае – нелинейная..
Кроме граничных условий, задаваемых на концах отрезка и называемых граничными условиями первого рода, используются еще условия на производные от решения на концах — граничные условия второго рода:
или линейная комбинация решений и производных – граничные условия третьего рода:
где 
– такие числа, что 
Возможно на разных концах отрезка использовать условия различных типов.
Наиболее распространены два приближенных метода решения краевой задачи:
— метод стрельбы (пристрелки);
Используя конечно-разностный метод, рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения второго порядка на отрезке [а; b].
Введем разностную сетку на отрезке [а; b]:
Решение задачи будем искать в виде сеточной функции:
предполагая, что решение существует и единственно.
Введем разностную аппроксимацию производных следующим образом:
Подставляя эти аппроксимации производных в исходное уравнение, получим систему уравнений для нахождения yk:
Приводя подобные члены и учитывая, что при задании граничных условий первого рода два неизвестных уже фактически определены, получим систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов:
Для этой системы уравнений при достаточно малых шагах сетки h и q(xk)
В первом случае линейная алгебраическая система аппроксимирует дифференциальную задачу в целом только с первым порядком (из-за аппроксимации в граничных точках), однако сохраняется трех диагональная структура матрицы коэффициентов. Во втором случае второй порядок аппроксимации сохраняется везде, но матрица линейной системы не трехдиагональная.
Пример. Решить краевую задачу:
с шагом 0,2.
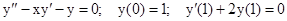
Во всех внутренних узлах отрезка [0; 1] после замены производных их разностными аналогами получим:
На левой границе y0 = 1, на правой границе аппроксимируем производную односторонней разностью 1-го порядка:
С помощью группировки слагаемых, приведения подобных членов и подстановки значений xk, а также с учётом у0 = 1,получим систему линейных алгебраических уравнений:
.
В результате решения системы методом Крамера в Excel, получим:
Решением краевой задачи является табличная функция:
| k | 0 | 1 | 2 | 3 | 4 | 5 |
| xk | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| yk | 1,0 | 0,772 | 0,583 | 0,431 | 0,313 | 0,223 |
Расчетная часть
3.1. Найти действительные корни уравнения 
методами простых итераций и касательных (Ньютона) с точностью до 0,00001.
Решение: Для нахождения корня уравнения предварительно отделим корень уравнения графическим методом, записав уравнение в виде:
Построим в осях ХОУ графики функций:
:
Линии графиков пересекаются в единственной точке с абсциссой х0, лежащей в интервале [0,5; 0,6], т.е.
Значение функции 
на концах интервала:
Т.к. знаки различны, то уравнение имеет единственный корень в интервале [0,5; 0,6].
3.1.1. Уточнение корня методом простых итераций.
Приведём исходное уравнение к виду:
Т.к. первая производная заданной функции 
в этом интервале положительна и численно первая производная на этом участке близка к 1,5, то константу С выбираем из интервала:
Т.о. итерационная функция приобретает вид:
Делаем первую итерацию:
Делаем вторую итерацию:
Делаем третью итерацию:
Делаем четвёртую итерацию:
Делаем пятую итерацию:
Делаем шестую итерацию:
Делаем седьмую итерацию:
Делаем восьмую итерацию:
Делаем девятую итерацию:
Продолжая далее, получаем:
На 19-ой итерации изменение шестого знака после запятой, позволяет утверждать, что пятый знак – после запятой – 5. Т.о. значение корня с заданной точностью:
3.1.2. Уточнение корня методом касательных (метод Ньютона):
Т.к. уравнение то же, то интервал, содержащий искомый корень, оставляем тот же [0,5; 0,6], т.е. а = 0,5; b = 0,6.
Находим первую и вторую производную функции 
:
Очевидно необходимые условия выполняются, т.к.:
, т.е. сохраняют знак на отрезке 
.
Выполняем первое приближение (х0 = 0,5):
Выполняем второе приближение (х1 = 0,571429):
Выполняем третье приближение (х2 = 0,576128:
Выполняем четвёртое приближение (х3 = 0,576146):
В пределах заданной точности f(x2) оказался равен нулю, т.е. требуемая точность достигнута за 4 шага. Значение корня с заданной точностью:
3.2. Вычислить приближенное значение интеграла 
, используя формулы:
а) трапеций (n = 10); б) Симпсона (n = 10); в) Гаусса (n = 5).
Решение: Ограничимся в расчётах 4 знаками после запятой. Для приближённого вычисления определённого интеграла методом трапеций используется формула:
Разобьём интервал (–1; 9) на n = 10 отрезков (h =1) и вычислим значения подынтегрального выражения для начала и конца каждого отрезка.
| № | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| х | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 | 2,4495 | 2,6458 | 3,7417 | 5,7446 | 8,3666 | 11,4455 | 14,8997 | 18,6815 | 22,7596 | 27,1109 | 31,7175 |
Тогда по формуле трапеций, имеем:
Используя формулу Симпсона (формулу параболических трапеций) в виде:
получим:
Применяя к исходному интегралу квадратурную формулу Гаусса, имеем:
где 
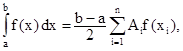
Для n = 5, коэффициенты ti, представляющие нули полинома Лежандра и коэффициента Аi (эти значения табулированы в справочных таблицах) составляют:
| i | 1 | 2 | 3 | 4 | 5 |
| ti | –0,9061 | –0,5385 | 0 | 0,5385 | 0,9061 |
| A1 | 0,2369 | 0,4786 | 0,5689 | 0,4786 | 0,2369 |
| хi | 0,4695 | 2,3075 | 5 | 7,6925 | 9,5305 |
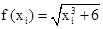 | 2,4705 | 4,2763 | 11,4455 | 21,4756 | 29,5239 |
3.3. Построить интерполяционные многочлены Лагранжа и Ньютона по следующим табличным данным:
 | 2,9 | 4,4 | 6,3 | 9,7 |
 | 2,84 | 4,53 | 6,04 | 5,50 |
Проверить совпадение значений интерполирующего многочлена с табличными значениями функции в узлах интерполяции.
Решение: Интерполяционный полином Лагранжа для четырёх узлов интерполяции записывается в виде:
Подставим численные значения из заданной таблицы:
Для составления интерполяционного полинома в форме Ньютона, вычислим разности первого порядка для заданной таблицы по формуле:
Вычислим разности второго порядка по формуле:
Вычислим разность третьего порядка по формуле:
Тогда интерполяционный полином Ньютона Ln(x) приобретает следующую форму:
Расчёты показывают, что оба интерполяционных полинома практически одинаковы, т.е. интерполяция ряда точек полиномом третьей степени осуществляется единственным образом.
По заданным узлам интерполяции хi значения полинома по этому уравнению составляют:
| х | 2,9 | 4,4 | 6,3 | 9,7 |
| Ln(x) | 2,840133 | 4,530614 | 6,041651 | 5,504897 |
| f(x) | 2,84 | 4,53 | 6,04 | 5,50 |
Расчётные значения практически совпадают с заданными значениями f(x).
По полученному уравнению построена кривая, проходящая через узлы интерполяции.
3.4. Найти оценки параметров линейной 
и квадратичной 
моделей функциональной зависимости величин у и х по результатам наблюдений 
, приведенным в таблице:
 | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 |
 | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 |
Построить чертеж: на плоскости нанести экспериментальные точки 
, построить графики полученных эмпирических функций 
.
Решение: Коэффициенты «a0 и а1» линейной модели найдём, выполнив необходимые вычисления. Расчеты сведем в таблицу:
| Номер наблюдения | 1 | 2 | 3 | 4 | 5 | Сумма |
| х | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 | 16 |
| у | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 | 11,2 |
| х 2 | 0,16 | 5,76 | 11,56 | 19,36 | 29,16 | 66 |
| х∙y | 0,856 | 5,136 | 7,616 | 10,296 | 12,636 | 36,54 |
 | 2,108 | 2,202 | 2,249 | 2,297 | 2,344 | 11,200 |
 | 0,0011 | 0,0039 | 0,0001 | 0,0019 | 0,0000 | 0,0069 |
Т.о. линейная зависимость у = а0 + а1х имеет вид: у = 2,08865 + 0,0473х.
По этой зависимости определены выровненные значения 
и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.
Коэффициенты а0, а1, а2 квадратичной зависимости найдём, также выполнив необходимые расчёты в таблице:
| Номер наблюдения | 1 | 2 | 3 | 4 | 5 | S |
| х | 0,4 | 2,4 | 3,4 | 4,4 | 5,4 | 16 |
| у | 2,14 | 2,14 | 2,24 | 2,34 | 2,34 | 11,2 |
| х 2 | 0,16 | 5,76 | 11,56 | 19,36 | 29,16 | 66 |
| х 3 | 0,064 | 13,824 | 39,304 | 85,184 | 157,464 | 295,84 |
| х 4 | 0,0256 | 33,1776 | 133,634 | 374,81 | 850,306 | 1391,95 |
| у·х | 0,856 | 5,136 | 7,616 | 10,296 | 12,636 | 36,54 |
| у·х 2 | 0,3424 | 12,3264 | 25,8944 | 45,3024 | 68,2344 | 152,1 |
| | 2,128 | 2,182 | 2,230 | 2,292 | 2,368 | 11,200 |
 | 0,0001 | 0,0018 | 0,0001 | 0,0023 | 0,0008 | 0,0051 |
Составим систему уравнений:
Решение этой системы методом Крамера даёт:
Т.о. квадратичная зависимость у = а0 + а1х + а2х 2 имеет вид:
у = 2,12433 + 0,00729·х + 0,006996·х 2 .
В нижней строке таблицы по полученному уравнению тоже рассчитаны значения 
по заданным значениям Х и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.
Эмпирическая ломаная, а также линии линейной и квадратичной модели построены на рисунке.
Результаты и выводы.
1. Т.о. интерполяционный полином Лагранжа и Ньютона, построенный по 4 заданным узлам интерполяции имеет вид:
Значения функции, вычисленные по этому полиному третьей степени, точно совпадают с заданными значениями в узлах интерполяции.
Полученное уравнение позволяет найти приближённые значения функции в любых промежуточных точках от х1 = 2,9 до х4 = 9,7.
2. Применение метода минимальных квадратов (МНК) к аппроксимации пяти экспериментальных точек линейной зависимостью вида у = а0 + а1х, т.е. прямой линией и квадратичной зависимостью вида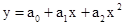 
, т.е. параболой дало следующие выражения:
– линейная зависимость реализована уравнением: у = 2,0887 + 0,0473х
– квадратичная зависимость реализована уравнением: у = 2,1243 + 0,0073·х + 0,007·х 2 .
Судя по остаточной сумме квадратов отклонений, квадратичная зависимость несколько лучше аппроксимирует экспериментальные данные, т.к. для неё остаточная сумма квадратов отклонений меньше, чем для линейной функции.
Список использованной литературы
1. Самарский А.А. Гулин А.В. Численные методы. М. МГУ. 1989 год.
2. Н. С. Бахвалов; Н.П. Жидков; Г.М. Кобельков. Численные методы. М 2003 год;
3. В.А. Буслов, С.Л.Яковлев. Численные методы и исследование функций. СПГУ. Курс лекций. СПБ 2001 г
4. Г.А. Зуева. Метод наименьших квадратов и его применение. Электронное учебное пособие. Иваново, 2009
Конечно-разностные аппроксимации производных (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
Конечно-разностные аппроксимации производных
Конечно-разностные аппроксимации производных (конечные разности) — способ приближенного вычисления частных производных
Выражения для конечных разностей можно получить из разложения функции в ряд Тейлора:
Или более коротко с использованием индексов точек:
Отсюда 
, где 
— остаток.
Отбрасывая остаток можно получить правую разность:
Погрешность такой аппроксимации определяется старшим членом в отброшенном остатке и в данном случае этот член содержит 
в первой степени.
Аналогичным образом, разлагая в ряд функцию 
можно получить:
Получим новую аппроксимацию первой производной:
которая называется левой разностью. У нее погрешность также определяется членом, содержащим в первой степени. Однако, если из выражения (1) вычесть (2), то можно получить более точную аппроксимацию первой производной, которая называется центральной разностью:
В этом случае член, определяющий погрешность аппроксимации, будет содержать во второй степени.
Аппроксимацию второй производной можно получить исходя из ее определения, — отношение приращения функции к приращению аргумента, где в качестве функции выступает аппроксимация первой производной. Также ее можно получить из выражений (1) и (2), если из (1) вычесть (2), отбросить члены содержащие производные старше второй, то получим:
Отброшенный остаток будет содержать член с во второй степени (после деления на 
)
Исходя из определения, можно получить выражения для третьей, четвертой и более старших разностей:
Для функции двух переменных выражения для конечных разностей, в предположении что первый индекс относится к координате 
, а второй — 
, будут выглядеть следующим образом:
- правая разность по оси
: 
; правая разность по оси : 
; левая разность по оси : 
; левая разность по оси : 
; центральная разность по оси : 
; центральная разность по оси : 
; вторая разность по оси : 
; вторая разность по оси : 
.Смешанная производная может быть получена следующим образом:
Алгоритм решения стационарных краевых задач методом конечных разностей
Метод конечных разностей — универсальный сеточный численный метод решения задач микроуровня.
Алгоритм решения стационарных краевых задач методом конечных разностей — последовательность действий, приводящая к решению стационарной задачи микроуровня
Нанесение на объект сетки или дискретизация пространства. Сетка — совокупность точек (узлов) дискретного пространства, аппроксимирующего непрерывное исходное пространство. Сетка выбирается таким образом, чтобы на ней легко можно было аппроксимировать производные с помощью конечных разностей. Как правило это равномерная прямоугольная сетка, но может быть и сетка заданная в полярных координатах, и неравномерная сетка, если таковая быстрее приводит к решению задачи. При наненсении сетки, если это возможно, следует учесть симметрию объекта. Это поможет сократить размерность аппроксимирующей системы уравнений. Нумерация узлов сетки. Для повышения эффективности решения в условиях использования свойства разреженности матрицы коэффициентов математической модели нумерацию следует проводить так, чтобы разность номеров соседних узлов была минимальной. Так, если двумерный объект имеет размер по оси 
больше, чем по оси 
, то нумерацию узлов нужно выполнять вдоль оси (вдоль короткой стороны). Запись разностного уравнения для каждого внутреннего узла сетки. При необходимости запись уравнений граничных условий для приграничных узлов. В результате должна быть получена замкнутая система, в общем случае, нелинейных алгебраических уравнений. Решение системы алгебраических уравнений.
Решение линейных одномерных стационарных краевых задач с помощью МКР
Предположим необходимо определить распределение температуры в стержне, теплоизолированном с цилиндрической стороны, и с заданной температурой на боковых гранях.
Одномерное стационарное уравнение теплопроводности для изотропной среды выглядит следующим образом:
В соотвествии с алгоритмом решения стационарных краевых задач методом конечных разностей наносим на объект равномерную сетку, как это показано на рис. 1.
Для каждого внутреннего узла сетки записываем разностный аналог исходного дифференциального уравнения:
- для узла 1:
для узла 2:
В результате получили замкнутую систему линейных алгебраических уравнений, где неизвестными являются 
и 
, а 
и 
— известные граничные условия.
Решив систему уравнений, получим 
и 
. Это решение является точным, поскольку в исходной постановке задача линейная.
Рассмотрим теперь решение задачи с краевым условием второго рода, на правой границе стержня задан тепловой поток:
Пусть 
и 
.
Запишем разностные аналоги для внутренних узлов сетки:
- для узла 1:
для узла 2Получили незамкнутую систему алгебраических уравнений (неизвестными являются , и ), дополнить которую можно разностным аналогом краевого условия (1).
Проще всего воспользоваться левой разностью:
Решая эту систему уравнений, получим 
, 
, 
.
Однако можно заметить, что аппроксимация задачи во внутренних узлах имеет второй порядок точности, а на границе — первый.
Можно вспомнить, что аппроксимация первой производной с помощью центральной разности имеет второй порядок точности, но для этого необходимо, чтобы граничный узел 3 был бы центральным узлом. Используется следующий прием: вводиться дополнительный фиктивный узел за пределами области, бывший граничный узел 3 становиться как бы внутренним (см. рис. 2)
Теперь можно записать следующую систему конечно-разностных уравнений:
- для узла 1:
для узла 2:
для узла 3:
граничное условие второго рода:
За повышение точности пришлось заплатить увеличением размерности системы конечно-разностных уравнений.
Решение нелинейных одномерных стационарных краевых задач с помощью МКР
Предположим необходимо определить распределение температуры в стержне, теплоизолированном с цилиндрической поверхности, и с заданной температурой на боковых гранях.
Одномерное стационарное уравнение теплопроводности для анизотропной среды выглядит следующим образом:
где 
— коэффициент теплопроводности.
Возможны нелинейности двух типов: коэффициент теплопроводности может зависеть от координаты (среда с неоднородными свойствами) и от температуры. Рассмотрим случай зависимости коэффициента теплопроводности от координаты на примере приближенного решения задачи об остываниии комнаты через окно с одинарным и двойным остеклением.
Предположим, что толщина стекла 
. Температура в комнате 
, на улице — 
Тепловой поток на улицу пропорционален градиенту температуры, то есть 
.
В соотвествии с алгоритмом решения стационарных краевых задач наносим на объект равномерную сетку, в предположении, что промежуток между стеклами равен двойной толщине стекла, как это показано на рис. 1.
Для каждого внутреннего узла сетки записываем разностный аналог исходного дифференциального уравнения:
- для узла 1:
для узла 2:
для узла 3:
В результате получили замкнутую систему линейных алгебраических уравнений, где неизвестными являются , и , а и 
— заданные граничные условия. Условно будем читать, что 
(реальные значения 
, 
).
Решив систему уравнений, получим 
, 
и 
. В этом случае градиент температуры составит 
, то есть двойное остекление в 20 раз эффективнее одинарного.
В том случае, когда коэффициент теплопроводности зависит от температуры, например для металлов он пропорционален ей, придем к следующей системе нелинейных алгебраических уравнений (для сетки из четырех узлов, два из которых внутренние):
- для узла 1:
для узла 2:
Данную систему придется решать итерационными методами.
Решение нестационарных одномерных задач с помощью МКР
Для решения нестационарных задач с помощью МКР используется та же идея дискретизации независимой переменной, что и при решении стационарных задач, в данном случае такой независимой переменной помимо пространства является время. На ось времени наносится сетка, в узлах которой выполняется аппроксимация частной производной по времени.
Но поскольку при этом возможны различные сочетания конечных разностей по оси координат и по времени, можно получить различные схемы решения нестационарных задач. Рассмотрим их на примере нестационарного уравнения теплопроводности:
Пусть при записи разностей нижний индекс соответствует оси , а верхний — оси времени.
Первый вариант разностного уравнения, апроксимирующего исходное (1):
называется явной разностной схемой, поскольку в этом уравнении всего одна неизвестная величина 
, которая может быть вычислена явным образом. Остальные переменные, входящие в уравнение (2) известны либо как начальные условия (при 
), либо с предыдущего временного слоя.
Второй вариант разностного уравнения, апроксимирующего исходное (1):
называется неявной разностной схемой, поскольку в этом уравнении несколько неизвестных величин, относящихся к 
-му временному слою. Для их нахождения придется записать систему разностных уравнений для всех внутренних узлов сетки, и решить ее.
Графическое изображение разностных уравнений получило название шаблонов решения сответствующих задач. В данном случае на рис. 1,а представлен шаблон явной разностной схемы, а на рис. 1,б — неявной.
Рис. 1. Шаблоны явной и неявной разностной схемы
Использование шеститочечного шаблона применено в схеме Кранка-Николсона:
В общем случае использования шеститочечного шаблона, имеем схему с весами:
которая при 
является неявной.
Примеры решения нестационарных задач с помощью МКР
Предположим необходимо определить изменение распределения температуры в стержне во времени (изменение температурного поля), теплоизолированном с цилиндрической стороны, с заданной температурой на боковых гранях (граничные условия) и заданной температурой 
стержня в нулевой момент времени (начальные условия).
Решим задачу с помощью явной разностной схемы.
Одномерное нестационарное уравнение теплопроводности для изотропной среды выглядит следующим образом:
Пусть , выберем значения шага по оси 
и значение шага по оси времени 
.
Наносим на объект равномерную сетку по оси , как это показано на рис. 1.
Записываем явную разностную схему для узла 1:
где 
— граничное условие, 
— начальные условия, отсюда 
.
Записываем явную разностную схему для узла 2:
где 
— граничное условие, — начальные условия, отсюда 
.
Таким образом найдено температурное поле в момент времени 
.
Аналогично для момента времени 
:
Для момента времени 
:
Получили картину прогревания стержня в течение трех единиц времени, представленную на рис. 2.
Результат явно не соответствует физическим процессам, произошло это из-за того, что явная разностная схема является неустойчивой. Неустойчивость выражается в том, что существует некоторое значение шага по времени, при превышении которого погрешность вычислений резко возрастает. Исследование устойчивости выходит за рамки этого изложения, но согласно литературе для данной задачи должно выполняться следующее соотношение:
Как нетрудно проверить, условие не было выполнено. Чтобы удостовериться в работоспособности явной разностной схемы, повторим вычисления для 
:
- для момента времени
; для момента времени 
для момента времени 
.Теперь картина прогревания не противоречит физическому смыслу задачи.
Аналитическое условие устойчивости можно получить только для простых модельных задач, но можно обеспечить устойчивость вычислений алгоритмически в том числе и для нелинейных задач следующим образом:
вычислить значения производных по времени во всех внутренних узлах объекта; определить максимальное из этих значений; разрешить измениться переменной в этом узле на некоторую заданную величину, которая определяется из физического смысла задачи. (Например для нашей задачи максимальной значение температуры внутри стержня 
, за один шаг по времени можем позволить измениться ей, допустим, на 
. Исходя из этого вычисляем значение 
); выполняем шаг по времени для всех узлов, изменение температуры во всех узлах не превысит разрешенной величины; если модельное время не закончилось переходим к пункту 1.
Рассмотрим решение задачи явной разностной схемой с граничными условиями второго рода (типа Неймана).
Предположим необходимо определить изменение распределения температуры в стержне во времени (изменение температурного поля), теплоизолированном с цилиндрической стороны, с заданной температурой с левой стороны, заданным тепловым потоком с правой (граничные условия) и заданной температурой стержня в нулевой момент времени (начальные условия)(см. рис. 3).
Краевые задачи и разностные схемы
з курсу “ Введение в численные методы ”
Тема: “КРАЕВЫЕ ЗАДАЧИ И РАЗНОСТНЫЕ СХЕМЫ”
1. Приведение к системе уравнений первого порядка
2. Разностное представление систем дифференциальных уравнений
3. Разностные системы уравнений для краевых задач
4. Краевые задачи второго порядка
5. Разностные схемы для уравнений в частных производных
6. Повышение точности разностных схем
7. Сеточные методы для нестационарных задач
1. Приведение к системе уравнений первого порядка
Для решения систем дифференциальных уравнений высокого порядка методами конечных разностей в первую очередь возникает потребность преобразования исходной системы в систему дифференциальных уравнений первого порядка с соответствующим образом преобразованными начальными или граничными условиями. И уже далее реализовывать численную процедуру решения.
Преобразование в систему уравнений первого порядка не единственно. Наиболее популярные из них в большинстве своем касаются линейных систем с постоянными или переменными коэффициентами. Основная идея всех методов состоит во введении новых переменных и выполнении замены высших производных этими переменными.
Пусть неоднородное дифференциальное уравнение высокого порядка задано в виде:
где 
– соответственно i- тая производная искомого решения и ее значение в начальный момент,
– функция, описывающая внешнее воздействие на динамический объект.
Обозначим первую производную искомой функции новой переменной 
, первую производную – следующей переменной: 
, первую производную – переменной 
и т.д.. Таким образом из исходной системы мы сформируем 
дифференциальное уравнение первого порядка:
При таких заменах производных искомой функции 
ее n -ная производная оказывается равной первой производной от 
:
В результате, эквивалентная система дифференциальных уравнений первого порядка примет следующий вид:
В случае, когда правая часть представлена взвешенной суммой функции 
и ее производных и в целом дифференциальное уравнение имеет вид
то его преобразование в систему уравнений первого порядка с новыми переменными 
осуществляется по следующим формулам:
Такое преобразование сохраняет коэффициенты исходного уравнения неизменными и исключает производные в правой части от . Начальные условия для новых переменных здесь приходится пересчитывать по достаточно сложным соотношениям.
И, наконец, приведем еще один вариант разложения на систему уравнений первого порядка исходного неоднородного уравнения с производными в правой части:
Замена переменных в отличие от предыдущего случая производится без сохранения коэффициентов исходного уравнения:
Производные искомой функции 
можно выразить через вновь введенные переменные 
путем многократного дифференцирования левой и правой части соотношения для y с подстановкой после каждого дифференцирования производных 
:
Умножив каждое выражение для 
на коэффициенты 
и просуммировав правые и левые члены равенств, получим уравнение, которое отличается от исходного лишь коэффициентами при производных в правых частях. Чтобы добиться тождественности, необходимо коэффициенты при соответствующих производных приравнять и разрешить полученную систему уравнений относительно неизвестных 
.
Система уравнений имеет вид:
В векторно-матричной форме это уравнение и его решение записываются в следующем виде:
где 
– вектор известных коэффициентов,
– вектор искомых коэффициентов,
– соответственно прямая и обратная верхне-треугольные матрицы коэффициентов. Первая из них выглядит так:
.
Обратная матрица удобна при использовании математических пакетов для решения векторно-матричного уравнения. Если 
, то коэффициенты 
легко вычисляются последовательной подстановкой значений , начиная с 
.
Начальные условия для 
вычисляются по выражениям для 
следующим образом:
или в векторно-матричной форме:
,
.
2. Разностное представление систем дифференциальных уравнений
Представление системы дифференциальных уравнений первого порядка с начальными условиями
можно заменить системой конечно-разностных уравнений первого порядка с целочисленной независимой переменной i ( 
):
,
погрешность аппроксимации которого пропорциональна сеточному шагу h .
Выше было уже показано, как можно уменьшить погрешность аппроксимации, делая ее пропорциональной 
. В частности это можно сделать, использовав среднее арифметическое двух разностей первого порядка: “вперед” и “ назад”.
При такой замене производной мы получаем систему разностных уравнений, состоящую из разностных уравнений второго порядка, требующих, кроме известного вектора начальных условий 
, еще один дополнительный вектор 
:
.
Дополнительный вектор начальных условий достаточно вычислить по формуле Эйлера. Он и определит дополнительное начальное условие с ошибкой, пропорциональной второй степени h :
Подстановка таких начальных условий в решение сохранит погрешность результатов на уровне . В таком случае говорят, что разностная схема имеет второй порядок точности.
3. Разностные системы уравнений для краевых задач
Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности — на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей.
Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной.
Для линейной системы уравнений первого порядка, записанной в матричной форме относительно вектора 
как
,
обязательно задается полный набор краевых условий 
, включающий хотя бы одно значение 
, или набор комбинаций из значений 
и
Обычно задаваемое граничное значение совмещается с тем или иным n- ным сеточным значением независимой переменной. Это позволяет обходиться без преобразования граничных условий к ближайшей точке сетки. Векторы 
, 
, 
и матрица 
в общем случае приводятся к единичному интервалу изменения независимой переменной с помощью линейного преобразования 
, в котором 
с шагом по оси абсцисс равном 
. Благодаря этому производные в левых частях единообразно заменяются (M+ 1)-точечными конечно-разностными выражениями через искомые значения решения:
.
Многоточечные представления производных получаются путем применения существующих соотношений между операторами дифференцирования, конечных разностей и сдвига:
Чтобы выразить значение производной порядка k в m -той точке целочисленного интервала [0, n ] через ординаты функции 
необходимо выполнить следующие операторные преобразования:
Заменив конечно-разностные операторы 
(после приравнивания нулю разностей со степенями выше n ) выражениями с оператором сдвига 
и вспомнив, что 
, получим в результате для k -той производной в m- той точке взвешенную сумму из ординат искомой функции:
.
Погрешность аппроксимации дифференциального оператора конечно-разностным оператором для центральной точки (m=n/ 2) пропорциональна с наименьшим коэффициентом величине 
и c наибольшим – для точек конца интервала.
Часто применяемые выражения конечно-разностной аппроксимации производных первого и второго порядков по трем-семи равномерно расположенным точкам приведены ниже в таблицах в виде коэффициентов, стоящих перед соответствующими ординатами функции. В левом верхнем углу таблиц записан общий множитель, а в крайней правой колонке – коэффициенты k 1, k 2для формул погрешности.
Трех точечная аппроксимация первой производной
 |  | |||
| y’(0) | -3 | 4 | -1 | 2 |
| y’(1) | -1 | 0 | 1 | -1 |
| y’(2) | 1 | -4 | 3 | 2 |
Четырех точечная аппроксимация первой производной
 |  |  |  |  |  |
 | -11 | 18 | -9 | 2 | -3 |
 | -2 | -3 | 6 | -1 | 1 |
 | 1 | -6 | 3 | 2 | -1 |
 | -2 | 9 | -18 | 11 | 3 |
Пятиточечная аппроксимация первой производной
 | | | | |  |  |
| | -25 | 48 | -36 | 16 | -3 | 12 |
| | -3 | -10 | 18 | -6 | 1 | -3 |
| | 1 | -8 | 0 | 8 | -1 | 2 |
| | -1 | 6 | -18 | 10 | 3 | -3 |
 | 3 | -16 | 36 | -48 | 25 | 12 |
Шести точечная аппроксимация первой производной
 | | | | | |  |  |
| | -137 | 300 | -300 | 200 | -75 | 12 | -10 |
| | -12 | -65 | 120 | -60 | 20 | -3 | 2 |
| | 3 | -30 | -20 | 60 | -15 | 2 | -1 |
| | -2 | 15 | -60 | 20 | 30 | -3 | 1 |
| | 3 | -20 | 60 | -120 | 65 | 12 | -2 |
 | -12 | 75 | -200 | 300 | -300 | 137 | 10 |
Семи точечная аппроксимация первой производной
 | | | | | | |  |   |
| | -147 | 360 | -450 | 400 | -225 | 72 | -10 | 60 |
| | -10 | -77 | 150 | -100 | 50 | -15 | 2 | -10 |
| | 2 | -24 | -35 | 80 | -30 | 8 | -1 | 4 |
| | -1 | 9 | -45 | 0 | 45 | -9 | 1 | -3 |
| | 1 | -8 | 30 | -80 | 35 | 24 | -2 | 4 |
| | -2 | 15 | -50 | 100 | -150 | 77 | 10 | -10 |
 | 10 | -72 | 225 | -400 | 450 | -360 | 147 | 60 |
Трех точечная аппроксимация второй производной
 | | | |  |
 | 1 | -2 | 1 | -12 , 2 |
 | 1 | -2 | 1 | 0 , -1 |
 | 1 | -2 | 1 | 12 , -2 |
Четырех точечная аппроксимация второй производной
 | | | | |  |
| | 2 | -5 | 4 | -1 | 55 , -6 |
| | 1 | -2 | 1 | 0 | -5 , -2 |
| | 0 | 1 | -2 | 1 | -5 , -2 |
 | -1 | 4 | -5 | 2 | 55 , -6 |
Пятиточечная аппроксимация второй производной
 | | | | | |  |
| | 35 | -104 | 114 | -56 | 11 | -150 , 12 |
| | 11 | -20 | 6 | 4 | -1 | 15 , -3 |
| | -1 | 16 | -30 | 16 | -1 | 0 , 2 |
| | -1 | 4 | 6 | -20 | 11 | 15 , 3 |
 | 11 | -56 | 114 | -104 | 35 | 150 , -12 |
Шести точечная аппроксимация второй производной
 | | | | | | |
| | 225 | -770 | 1070 | -780 | 305 | -50 |
| | 50 | -75 | -20 | 70 | -30 | 5 |
| | -5 | 80 | -150 | 80 | -5 | 0 |
| | 0 | -5 | 80 | -150 | 80 | -5 |
| | 5 | -30 | 70 | -20 | -75 | 50 |
 | -50 | 305 | -780 | 1070 | -770 | 225 |
Семи точечная аппроксимация второй производной
 | | | | | | | |
| | 812 | -3132 | 5265 | -5080 | 2970 | -972 | 137 |
| | 137 | -147 | -255 | 470 | -285 | 93 | -13 |
| | -13 | 228 | -420 | 200 | 15 | -12 | 2 |
| | 2 | -27 | 270 | -490 | 270 | -27 | 2 |
| | 2 | -12 | 15 | 200 | -420 | 228 | -13 |
| | -13 | 93 | -285 | 470 | -255 | -147 | 137 |
 | 137 | -972 | 2970 | -5080 | 5265 | -3132 | 812 |
Например, производная первого порядка 
в точках m =0, 3, 5 для семи точечной аппроксимации будет иметь вид:
,
.
Аналогично выписываются выражения и для вторых производных в точках 0 и 2:
Таким образом, из приведенных таблиц можно выбрать аппроксимирующие выражения для производной в данной точке, включающие значения функции в точках нужного окружения.
4. Краевые задачи для уравнений второго порядка
При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями.
Преобразование их в конечно-разностную систему алгебраических уравнений осуществляется аналогично: для каждой точки в области (интервале) интегрирования, где не задано краевое или граничное значение искомой функции, записывается исходное уравнение, в котором все производные выражены через заранее определенное число близлежащих ординат искомой функции, принадлежащих области, и вычислены все коэффициенты и функции независимых переменных в этой точке. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области. В результате будет сформирована алгебраическая система уравнений с числом уравнений и неизвестных, равном общему числу точек области интегрирования.
В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Это достигается многократным применением оператора сдвига к соответствующему конечно-разностному оператору.
Если в центральных точках точность аппроксимации производных с n точками удовлетворяет поставленным требованиям и эту точность желательно сохранить и в приграничных точках заданных областей, то для последних выбирают аппроксимирующие формулы, построенные для (n +1)— й точки или более.
Рассмотрим примеры аппроксимации дифференциальных уравнений с краевыми условиями конечно-разностной системой алгебраических уравнений. Эти аппроксимации в литературе получили название «разностные схемы». Ниже в четырех таблицах приведены четыре варианта конечно-разностной аппроксимации одной и той же краевой задачи, для которой известно точное решение. Вид уравнения, условия на границе интервала, решение аналитическое и вычисленное в заданных точках с 12 значащими цифрами приведены в правой крайней колонке первой таблицы. В левых колонках первой и в трех остальных таблицах записаны системы алгебраических уравнений, полученных применением трех-, пяти-, пяти-шести- и семи точечной аппроксимации второй производной в заданном уравнении. Справа от уравнений приведены решения алгебраических уравнений тоже с 12-ю значащими цифрами.
| Система уравнений с трехточечным представлением производных | Вектор разностного решения с шагом h =0.1 |  |
-199  +100  +0.1=0 | 0.0186590989712 | 0.0186415437361 |
100 -199 +100  +0.2=0 | 0.0361316064473 | 0.0360976603850 |
100 -199 +100  +0.3=0 | 0.0512427953890 | 0.0511947672548 |
100 -199 +100  +0.4=0 | 0.0628415300546 | 0.0627828520998 |
100 -199 +100  +0.5=0 | 0.0698118753674 | 0.0697469636621 |
100 -199 +100  +0.6=0 | 0.0710840847137 | 0.0710183518969 |
100 -199 +100  +0.7=0 | 0.0656455142231 | 0.0655851465687 |
100 -199 +100  +0.8=0 | 0.0525504484304 | 0.0525024675253 |
| 100 -199 +0.9=0 | 0.0309298757856 | 0.0309018656257 |
Система уравнений для пяти-точечного | Вектор решения |
| -9940 +3000 +2000 -500 +6=0 | 0.0186406186406 |
| 8000 -14940 +8000 -500 +12=0 | 0.0360968696594 |
| -500 +8000 -14940 +8000 -500 +18=0 | 0.0511941848390 |
| -500 +8000 -14940 +8000 -500 +24=0 | 0.0627825213460 |
| -500 +8000 -14940 +8000 -500 +30=0 | 0.0697468774179 |
-500 +8000 -14940 +8000 -500  8+36=0 | 0.0710184988305 |
| -500 +8000 -14940 +8000 -500 +42=0 | 0.0655854996422 |
| -500 +8000 -14940 +8000 +48=0 | 0.0525029672554 |
| -500 +2000 +3000 -9940 +54=0 | 0.0309024932693 |
| Система уравнений для пяти- и шести точечного представления производных | Вектор решения |
| -3720 -1000 +3500 -1500 +250+3=0 | 0.0186415486274 |
| 8000 -14940 +8000 -500 +12=0 | 0.0360976918947 |
| -500 +8000 -14940 +8000 -500 +18=0 | 0.0511948294923 |
| -500 +8000 -14940 +8000 -500 +24=0 | 0.0627829167486 |
| -500 +8000 -14940 +8000 -500 +30=0 | 0.0697469746974 |
| -500 +8000 -14940 +8000 -500 +36=0 | 0.0710183243686 |
| -500 +8000 -14940 +8000 -500 +42=0 | 0.0655851063829 |
| -500 +8000 -14940 +8000 +48=0 | 0.0525024168959 |
| 250 -1500 +3500 -1000 -3720 +27=0 | 0.0309018105849 |
| Система уравнений для семиточечного представления производных | Вектор решения |
| -7260 -12750 +23500 -14250 +4650 -650+9=0 | 0.0186415513486 |
| 11400 -20910 +10000 +750 -600 +100+18=0 | 0.0360976659970 |
| -1350 +13500 -24410 +13500 -1350 +100+27=0 | 0.0511947713313 |
| 10 -135 +1350 -2441 +1350 -135 +10+3.6=0 | 0.0627828547351 |
| 10 -135 +1350 -2441 +1350 -135 +10+4.5=0 | 0.0697469648318 |
| 10 -135 +1350 -2441 +1350 -135 +10+5.4=0 | 0.0710183515790 |
| 100 -1350 +13500 -24410 +13500 -1350+63=0 | 0.0655851447467 |
| 100 -600 +750 +10000 -20910 +11400+72=0 | 0.0525024640963 |
| -650 +4650 -14250 +23500 -12750 -7260+81=0 | 0.0309018602217 |
В этой задаче весь интервал интегрирования [0,1] был разбит на 10 равных частей с шагом h =0.1. Из одиннадцати точек в двух крайних искомая функция x (t ) была задана, поэтому уравнения записывались для девяти внутренних точек, в которых значения функции требовалось найти.
5. Разностные схемы для уравнений в частных производных
Конечно-разностная аппроксимация дифференциальных уравнений в частных производных, называемая в литературе методом сеток , использует те же конечно-разностные выражения производных через значения искомой функции, которые приведены в таблицах выше. Однако есть особенности, которые связаны с наличием у каждой рассматриваемой точки соседних точек не только по направлениям осей независимых переменных, но и во множестве других наклонных направлений.
Поэтому, в случае использования многоточечных (более трех точек) формул для производных, выражения последних могут разрабатываться дополнительно для каждого применения.
Наиболее удобным в разработке многоточечных конечно-разностных выражений для уравнений в частных производных является операторный метод, основанный на учете взаимосвязи оператора дифференцирования с операторами сдвига по направлениям различных независимых переменных. Рассмотрим его применение на примере построения разностных формул для двумерных уравнений в частных производных второго порядка.
Характерным представителем уравнений в частных производных второго порядка является уравнение Лапласа:
,
где 
– непрерывная функция, заданная на границе области.
Область численного решения уравнения разобьем на клетки системой вертикальных и горизонтальных прямых, проходящих через равномерно расположенные с шагом h точки на осях координат соответственно x и y :
Значения функции в узлах сетки обозначим через 
и для каждой точки области решений частные производные из уравнения заменим соответствующим (например, трех точечным) симметричным конечно-разностным выражением для внутренних точек и для точек вблизи границ таким несимметричным, чтобы значения функций не выходили за пределы области:
После подстановки в уравнение Лапласа этих выражений для каждой внутренней точки области будет получена система алгебраических уравнений следующего вида:
В качестве примера, демонстрирующего применение метода сеток, приведем решение уравнения Лапласа для прямоугольной области с количеством узлов 
и значениями функции на границе, как показано ниже:
| u(0,0) | 0.5 | 0.476 | 0.404 | 0.294 | 0.154 | 0 |
| 0.5 | u(1,1) | u(1,2) | u(1,3) | u(1,4) | u(1,5) | 0 |
| 0.476 | u(2,1) | u(2,2) | u(2,3) | u(2,4) | u(2,5) | 0 |
| 0.404 | u(3,1) | u(3,2) | u(3,3) | u(3,4) | u(3,5) | 0 |
| 0.294 | u(4,1) | u(4,2) | u(4,3) | u(4,4) | u(4,5) | 0 |
| 0.154 | u(5,1) | u(5,2) | u(5,3) | u(5,4) | u(5,5) | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Уравнения для 25 внутренних точек u (i,k ):
http://pandia.ru/text/78/456/60104.php
http://www.zinref.ru/000_uchebniki/02800_logika/011_lekcii_raznie_51/248.htm