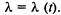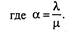Записать систему дифференциальных уравнений колмогорова

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Уравнения Колмогорова

2.1 Уравнения Колмогорова

Рассмотрим математическое описание марковского случайного процесса с дискретными состояниями системы S_o, S_l_, S₂(см. рис. 6.2.1) и непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния S_i в состояние Sj происходят под воздействием простейших потоков событий с интенсивностями λ_ij, а обратный переход под воздействием другого потока λ_ij,. Введем обозначение p_i как вероятность того, что в момент времени t система находится в состоянии S_i_. Для любого момента времени t справедливо записать нормировочное условие—сумма вероятностей всех состояний равна 1:

Проведем анализ системы в момент времени t, задав малое приращение времени Δt, и найдем вероятность р₁ (t+ Δt) того, что система в момент времени (t+ Δt) будет находиться в состоянии S₁ которое достигается разными вариантами:

а) система в момент t с вероятностью p₁(t) находилась в состоянии S₁ и за малое приращение времени Δt так и не перешла в другое соседнее состояние — ни в S₀, ни b S₂. Вывести систему из состояния S₁ можно суммарным простейшим потоком c интенсивностью (λ₁₀ +λ₁₂), поскольку суперпозиция простейших потоков также является простейшим потоком. На этом основании вероятность выхода из состояния S₁ за малый промежуток времени Δ t приближенно равна (λ₁₀ +λ₁₂)* Δ t. Тогда вероятность невыхода из этого состояния равна [1 -(λ₁₀ +λ₁₂)* Δ t].B соответствии с этим вероятность того, что система останется в состоянии Si на основании теоремы умножения вероятностей, равна:

б)система находилась в соседнем состоянии S_o и за малое время Δ t перешла в состояние S_o Переход системы происходит под воздействием потока λ₀₁ с вероятностью, приближенно равной λ₀₁Δ t

Вероятность того, что система будет находиться в состоянии S₁, в этом варианте равна p_o(t) λ ₀₁ Δ t;

в) система находилась в состоянии S₂ и за время Δ t перешла в состояние S₁ под воздействием потока интенсивностью λ ₂₁ с вероятностью, приближенно равной λ₂₁Δ t. Вероятность того, что система будет находиться в состоянии S₁, равна p₂(t) λ₂₁Δ t.

Применяя теорему сложения вероятностей для этих вариантов, получим выражение:

которое можно записать иначе:

Переходя к пределу при Δt -> 0, приближенные равенства перейдут в точные, и тогда получим производную первого порядка

что является дифференциальным уравнением.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:

Для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО S_i в функции времени p_i(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы, в этом состоянии. Если предельная вероятность состояния S₀ – равна p₀ = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S_o. Например, при отсутствии заявок на обслуживание к = 0, р₀ = 0,2,; следовательно, в среднем 2 ч в день система находится в состоянии S_o и простаивает, если продолжительность рабочего дня составляет 10 ч.

Поскольку предельные вероятности системы постоянны, то заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО. Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность р_i рассматриваемого состояния Si умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) изданного состояния S_iсистему, а справа от знака равенства — сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние Si систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1:_n

Например, для СМО, имеющей размеченный граф из трех состояний S_o, S₁, S₂ рис. 6.2.1, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:

К этим уравнениям надо добавить еще начальные условия. Например, если при t = 0 система S находится в состоянии S_1, то начальные условия можно записать так:

Переходы между состояниями СМО происходит под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение времени Δ t, т.е. величиной элемента вероятности перехода λ_ij Δ t, где λ_ij — интенсивность потока событий, переводящих систему из состояния i в состояние i (по соответствующей стрелке на графе состояний).

Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет марковским случайным процессом, т.е. процессом без последствия. В этом случае поведение системы достаточно просто, определяется, если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все вероятности состояний как функции времени:

Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что существует

независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t->∞ и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои, состояния, но каждое из этих состояний осуществляется с некоторой постоянной вероятностью, определяемой средним временем пребывания системы в каждом из состояний.

Вычислить предельные вероятности состояния р_i можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t-> ∞ зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему Обычных линейных алгебраических уравнений, которая совместно с нормировочным условием позволяет вычислить все предельные вероятности состояний.

Решение. Согласно приведенному мнемоническому правилу система дифференциальных уравнений Колмогорова имеет вид

Согласно приведенному мнемоническому правилу система дифференциальных уравнений Колмогорова имеет вид

Начальные условия при

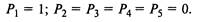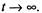
Рассмотрим, что произойдет с системой описываемой дифференциальными уравнениями Колмогорова, при Известно, что в случае сообщающихся состояний функции стремятся к предельным (финальным) вероятностям состояний системы Финальные вероятности не зависят от времени. Поэтому в системе дифференциальных уравнений Колмогорова все левые части уравнений (производные) принимают равными нулю. При этом система дифференциальных уравнений превратится в систему линейных алгебраических уравнений.

Для нашего примера система (2.9) будет иметь вид

Решая ее с учетом условия получим

все предельные вероятности. Эти вероятности представляют собой не что иное, как среднее относительное время пребывания системы в данном состоянии.

Рис. 2.5. Граф состояний системы S

Состояния Si, S₂ и S₅ — несущественные, так как из S_<можно уйти, например, в состояние S₂ и не вернуться, а из состояния S₂ — в состояние 5₃ или 5₄ и не вернуться, аналогично из состояния S₅ — в состояние 5₆ и З^. Состояния 5₃, 5₄, 5₆ и S₇ — существенные состояния.

Теорема. При конечном числе состоянии для существования финальных вероятностей необходимо и достаточно, чтобы из каждого существенного состояния можно было (за какое-то число шагов) перейти в каждое другое существенное состояние. Граф из примера рис. 2.5 этому условию не удовлетворяет, так как из существенного состояния S₄ нельзя перейти в существенное состояние S₇. Если система S имеет конечное число состояний S^ S₂, . S_n, то для существования финальных вероятностей достаточно, чтобы из любого состояния системы можно было (за какое-то число шагов) перейти в любое другое состояние.

Если число состояний S_<, S₂, . S_n бесконечно, то это условие перестает быть достаточным, и существование финальных вероятностей зависит не только от графа состояний, но и от интенсивности А,0.

При исследовании непрерывных марковских цепей, как было уже отмечено, часто бывает удобно представить переход системы из состояния в состояние как воздействие каких-то потоков событий (поток заявок на обслуживание, поток автомобилей, поток документов и т. п.). Различают следующие основные свойства, которыми могут обладать случайные потоки событий:

Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событий на участок времени т зависит только от длины участка и не зависит от расположения на оси О/. Другими словами, стационарность означает неизменность вероятностного режима потока событий во времени. Поток, обладающий свойством стационарности, называют стационарным. Для стационарного потока среднее число событий, воздействующих на систему в течение единицы времени, остается постоянным. Реальные потоки событий в экономике предприятия являются в действительности стационарными лишь на ограниченных участках времени.

Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка. Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток, обладающий свойством ординарности, называют ординарным. Реальные потоки событий в различных экономических системах либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.

Отсутствие последействия — это свойство потока, которое состоит в том, что для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени. Поток, обладающий свойством отсутствия последействия, называют потоком без последействия. Поток событий, одновременно обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим потоком событий.

Под интенсивностью потока понимают

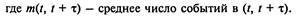Для простейшего потока интенсивность Если поток

событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком, а его интенсивность зависит от времени, т. е.

В пуассоновском потоке событий (стационарном и нестационарном) число событий потока, попадающих на любой участок, распределено по закону Пуассона:

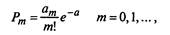Для простейшего потока а для нестационарного пуассо-

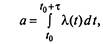Отметим еще одно важное свойство простейшего потока событий. Промежуток времени / между соседними событиями распределен по показательному закону, а его среднее значение и среднее квадратическое отклонение а равны, т. е.

где — интенсивность потока.

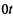Рассмотрим еще одну типичную схему непрерывных марковских цепей, так называемую схему гибели и размножения, часто встречающуюся в разнообразных практических задачах.

Марковский процесс с дискретными состояниями . S_n называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку, в которой каждое из средних состояний может переходить только в соседние со-

стояния, которые, в свою очередь, переходят обратно, а крайние состояния переходят только в соседние состояния (рис. 2.6).

Рис. 2.6. Граф состояний для процесса гибели и размножения

Название взято из биологических задач, где состояние популяции означает наличие в ней единиц особей.

Переход вправо связан с размножением единиц, а влево — с их гибелью.

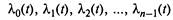
— интенсивности размножения, — интенсивности гибели.

У X и [I индекс того состояния, из которого стрелка выходит.

С состоянием связана неслучайная величина если система в момент времени / находится в состоянии , то дискретная случайная величина , связанная с функционированием системы, принимает значение к. Таким образом, получаем случайный процесс , который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

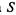
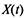
Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

Пример 2.4. Рассмотрим эксплуатацию моделей автомобилей одной марки в крупной транспортной фирме (на предприятии). Интенсивность поступления автомобилей на предприятие равна Каждый поступивший на предприятие автомобиль списывается через случайное время Срок службы автомобиля распределен по показательному закону с параметром Процесс эксплуатации автомобилей является случайным процессом. — число автомобилей данной марки, находящихся в эксплуатации в момент t.

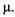
Найдем одномерный закон распределения случайного процесса если:

1) нет ограничений на число эксплуатируемых машин;

2) на предприятии может эксплуатироваться не более п автомобилей.

1. Случайный процесс эксплуатации автомобилей есть процесс гибели и размножения, размеченный граф которого представлен на рис. 2.7.

Рис. 2.7. Граф состояний

Система уравнений Колмогорова, соответствующая этому графу, имеет вид

Если в начальный момент времени на предприятии не бы-

ло ни одного автомобиля, то решать эту систему уравнений нужно при начальных условиях Если при

на предприятии было автомобилей то началь-

ные условия будут иметь вид

2. Если на предприятии может эксплуатироваться не более п автомобилей моделей одной марки, то имеет место процесс гибели и размножения с ограниченным числом состояний л, размеченный граф которого представлен на рис. 2.8.

Рис.2.8. Граф состояний

Система уравнений Колмогорова для размеченного графа (рис. 2.8) имеет вид:

Эту систему надо решать при начальных условиях, рассмотренных выше. Решения систем уравнений (2.15) и (2.16) являются одномерными законами распределения 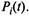Отыскание решений систем (2.15) и (2.16) в общем виде при произвольном виде функции

представляет значительные трудности и не имеет практических приложений.

При постоянных интенсивностях потоков гибели и размножения и конечном числе состояний будет существовать стационарный режим. Система S с конечным числом состояний (п + 1), в которой протекает процесс гибели и размножения с постоянными интенсивностями потоков гибели и размножения, является простейшей эргодической системой. Размеченный граф состояний для такой системы представлен на рис. 2.9.

Предельные (финальные) вероятности состояний для простейшего эргодического процесса гибели и размножения, находящегося в стационарном режиме, определяются по следующим формулам:

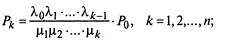Рис.2.9. Граф состояний

Правило. Вероятность к-то состояния в схеме гибели и размножения равна дроби, в числителе которой стоит произведение всех интенсивностей размножения, стоящих левее , а в знаменателе — произведение всех интенсивностей гибели, стоящих левее , умноженной на вероятность крайнего левого состояния системы

В примере 2.4 для стационарного режима если интенсивность поступления автомобилей постоянная то фи-

нальные вероятности состояний при условии, что нет ограничений на число автомобилей на предприятии, равны:

При этом математическое ожидание числа эксплуатируемых автомобилей равно его дисперсии:

Если существует ограничение по числу автомобилей на предприятии (не более я), то финальные вероятности равны

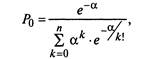Математическое ожидание числа эксплуатируемых автомобилей в стационарном режиме

Пример 2.5.В состав ЭВМ входят четыре накопителя на магнитных дисках (НМД). Бригада в составе четырех человек обслуживающего персонала проводит профилактический ремонт каждого диска. Суммарный поток моментов окончания ремонтов для всей бригады — пуассоновский с интенсивностью . После окончания ремонта диск проверяется; с вероятностью Р он оказывается работоспособным (время проверки мало, и им можно пренебречь по сравнению со временем профилактики). Если диск оказался неработоспособным, то вновь проводится его профилактика (время на которую не зависит от того, проводилась ли она ранее) и т.д. В начальный момент все НМД нуждаются в профилактическом ремонте 1 .