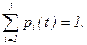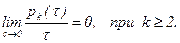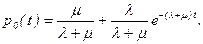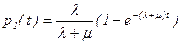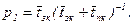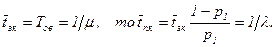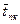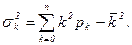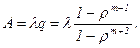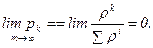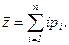Записать систему уравнений колмогорова для графа

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

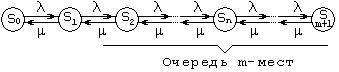
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Уравнения Колмогорова

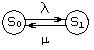
Рассмотрим математическое описание марковского случайного процесса с дискретными состояниями системы S₀, S₁, S₂ (см. рис. 6.2.1) и непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностями l_ij, а обратный переход — под воздействием другого потока l_ij, Введем обозначение р_i как вероятность того, что в момент времени t система находится в состоянии S_i. Для любого момента времени t справедливо записать нормировочное условие — сумма вероятностей всех состояний равна 1:

Проведем анализ системы в момент времени t, задав малое приращение времени Dt, и найдем вероятность p₁(t + Dt) того, что система в момент времени (t + Dt) будет находиться в состоянии S₁, которое достигается разными вариантами:

а) система в момент t с вероятностью p_i(t) находилась в состоянии S_i и за малое приращение времени Dt так и не перешла в другое соседнее состояние — ни в S₀, ни в S₂. Вывести систему из состояния S₁ можно суммарным простейшим потоком с интенсивностью (l₁₀ + l₁₂) , поскольку суперпозиция простейших потоков также является простейшим потоком. На этом основании вероятность выхода из состояния S₁ за малый промежуток времени Dt приближенно равна (l₁₀ + l₁₂)×Dt. Тогда вероятность невыхода из этого состояния равна [1 — (l₁₀ + l₁₂) × Dt]. В соответствии с этим вероятность того, что система останется в состоянии S₁ на основании теоремы умножения вероятностей, равна:

б) система находилась в соседнем состоянии S₀ И за малое время Dt перешла в состояние S₁. Переход системы происходит под воздействием потока l₀₁ c вероятностью, приближенно равной l₀₁ Dt.

Вероятность того, что система будет находиться в состоянии S₁, в этом варианте равна p₀(t) l₀₁Dt;

в) система находилась в состоянии S₂ и за время Dt перешла в состояние S₁ под воздействием потока интенсивностью l₂₁ с вероятностью, приближенно равной l₂₁Dt. Вероятность того, что система будет находиться в состоянии S₁, равна p₂(t)l₂₁Dt.

Применяя теорему сложения вероятностей для этих вариантов, получим выражение:

которое можно записать иначе:

Переходя к пределу при А/ -^ О, приближенные равенства перейдут в точные, и тогда получим производную первого порядка

что является дифференциальным уравнением.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:

Для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО S_i в функции времени p_i(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы в этом состоянии. Если предельная вероятность состояния S₀ равна p₀ = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S0. Например, при отсутствии заявок на обслуживание k = 0, p0 = 0,2, следовательно, в среднем 2 ч в день система находится в состоянии S₀ и простаивает, если продолжительность рабочего дня составляет 10 ч.

Поскольку предельные вероятности системы постоянны, то, заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО. Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность р_i рассматриваемого состояния S₁ умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) из данного состояния S_i систему, а справа от знака равенства — сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние S_i систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1:

Например, для СМО, имеющей размеченный граф из трех состояний S₀, S₁, S₂ рис. 6.2.1, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:

Пример 1. Составим систему уравнений Колмогорова в общем виде для случая, когда граф состояний имеет вид (рис. 6.2.2):

Плотность вероятностей этих переходов указана рядом с соответствующими стрелками. Пользуясь приведенными выше правилами, получаем систему уравнений:

К этим уравнениям надо добавить еще начальные условия. Например, если при t = 0 система S находится в состоянии S₁, то начальные условия можно записать так:

Переходы между состояниями СМО происходят под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение времени Dt, т.е. величиной элемента вероятности перехода l_ij Dt, где l_ij — интенсивность потока событий, переводящих систему из состояния / в состояние j (по соответствующей стрелке на графе состояний).

Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет марковским случайным процессом, т.е. процессом без последствия. В этом случае поведение системы достаточно просто определяется, если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все вероятности состояний как функции времени:

Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что существует

независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t®¥ и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои состояния, но каждое из этих состояний осуществляется с некоторой постоянной вероятностью, определяемой средним временем пребывания системы в каждом из состояний.

Вычислить предельные вероятности состояния p_i можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t®¥ зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему обычных линейных алгебраических уравнений, которая совместно с нормировочным условием позволяет вычислить все предельные вероятности состояний.

Пример 2. Запишем систему алгебраических уравнений для вычисления предельных вероятностей состояний системы, изображенной на рис. 6.2.2.

Для этого допустим, что

= 0 (i = 1; 2; 3; 4),

тогда из записанной ранее в примере 1 системы уравнений Колмогорова получаем:

l21p23 — l12p1 =0,

l12p1 + l23p^3 — (l21 + l23)p2 =0,

l23p2 + l43p4 -(l32 +l34)p3 =0,

И, Кроме того, мы должны учесть нормировочное условие:

Любое из уравнений записанной системы можно исключить, использовав вместо него нормировочное условие.

Предмет, цель и задачи теории массового обслуживания

Во многих областях экономики, финансов, производства и быта важную роль играют системы специального вида, реализующие многократное выполнение однотипных задач. Подобные системы называют системами массового обслуживания (СМО). В качестве примеров СМО в финансово- экономической сфере можно привести системы, представляющие собой банки, страховые организации, налоговые инспекции, аудиторские службы. В сфере производства и обслуживания примерами СМО могут служить: различные системы связи (телефонные станции), погрузочно-разгрузочные комплексы, автозаправочные станции, магазины, парикмахерские, билетные кассы, пункты обмена валюты, и т.д. Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.

Каждая СМО включает в свою структуру некоторое число обслуживающих устройств, которые называют каналами (приборами, линиями) обслуживания. Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, парикмахеры), линии связи, машины, краны, ремонтные бригады, железнодорожные пути и т.д.

СМО могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а случайные моменты времени. Обслуживание заявок, также длится не постоянное, заранее известное время, а случайное время, которое зависит от многих случайных причин. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО: на входе СМО могут скапливаться необслуженные заявки, что приводит к перегрузке СМО, а при свободных каналах на входе СМО заявки не будет, что приводит к недогрузке СМО, т.е. к простаиванию ее каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными.

Во всякой СМО можно выделить следующие основные элементы:

1) входящий поток заявок;

3) каналы обслуживания;

4) выходящий поток обслуженных заявок.

Каждая СМО в зависимости от своих параметров — характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.

Предметом изучения теории массового обслуживания является СМО.

Цель теории массового обслуживания — выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.

Для достижения этой цели решаются задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.

В качестве характеристик эффективности функционирования СМО можно, выбрать три основные группы (обычно средних) показателей:

1. Показатели эффективности использования СМО:

1.1. Абсолютная пропускная способность СМО — среднее число заявок, которое может обслужить СМО в единицу времени.

1.2. Относительная пропускная способность СМО — отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших заявок за это же время.

1.3. Средняя продолжительность периода занятости СМО.

1.4. Коэффициент использования СМО — средняя доля времени, в течение которого СМО занята обслуживанием заявок.

2. Показатели качества обслуживания заявок:

2.1. Среднее время ожидания заявки в очереди.

2.2. Среднее время пребывания заявки в СМО.

2.3. Вероятность отказа заявке в обслуживании без ожидания.

2.4. Вероятность того, что поступившая заявка немедленно будет принята к обслуживанию.

2.5. Закон распределения времени ожидания заявки в очереди.

2.7. Закон распределения времени пребывания заявки в СМО.

2.8. Среднее число заявок, находящихся в очереди.

2.9. Среднее число заявок, находящихся в СМО.

3. Показатели эффективности функционирования пары «СМО — по-требитель», где под потребителем понимают всю совокупность заявок или некий их источник (например, средний доход, приносимый СМО в единицу времени, и т.п.).

Отметим, что третья группа показателей оказывается полезной в тех случаях, когда некоторый доход, получаемый от обслуживания заявок, и затраты на обслуживание измеряются в одних и тех же единицах. Эти показатели обычно носят вполне конкретный характер и определяются спецификой СМО, обслуживаемых заявок и дисциплиной обслуживания.

Случайный характер потока заявок и длительности их обслуживания порождает в СМО случайный процесс.

Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае — моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае — состояние СМО).

Для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т. е. построить и проанализировать его математическую модель.

Математическое изучение функционирования СМО значительно упрощается, если протекающий в ней случайный процесс является марковским. В этом случае работа СМО сравнительно легко описывается с помощью аппарата конечных систем обыкновенных линейных дифференциальных уравнений первого порядка, а в предельном режиме (при достаточно длительном функционировании СМО) — с помощью аппарата конечных систем линейных алгебраических уравнений, и в результате удается выразить в явном виде основные характеристики эффективности функционирования СМО через параметры СМО, потока заявок и дисциплины работы СМО.

Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воздействием которых происходят переходы системы из состояния в состояние, были пуассоновскими. В СМО потоками событий являются потоки заявок, потоки «обслуживания» заявок и т.д.

6. Потоки событий

Процесс работы СМО представляет собой случайный процесс. Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями. Переводы СМО из одного состояния в другое происходят под воздействием событий — поступления заявок и их обслуживания. Последовательность появления событий, следующих одно за другим в случайные моменты времени, формирует так называемый ноток событий. Под потоком событий понимается последовательность однородных событий, следующих одно за другим в случайные моменты времени. Обычно поведение системы обычно определяется не одним, а сразу несколькими потоками. Так, например, обслуживание клиентов в ателье определяется потоком посетителей и потоком обслуживания; в этих потоках случайными явля-ются моменты появления клиентов, время ожидания в очереди и время, затрачиваемое на обслуживание каждого клиента. Поток характеризуется интенсивностью X — частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным.

Поток событий называется стационарным, если вероятность появления к событий за промежуток времени длительностью I зависит только от длительности промежутка t и не зависит от начала отсчета. Стационарность потока означает независимость от времени его вероятностных характеристик.

Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени DeltaT двух и более событий пренебрежимо мала по сравнению с вероятностью попадания только одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами. Например, поток поездов, подходящих к станции, ординарен, а поток вагонов не ординарен.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени t1 и t2

число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Например, поток покупателей, входящих в магазин, можно считать потоком без последействия потому, что причины, обусловившие приход каждого из них, не связаны с аналогичными причинами других покупателей.

Поток событий называется простейшим (или пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. Название «простейший» объясняется тем, что СМО с простейшими потоками имеет

8. Системы массового обслуживания

Классификация систем массового обслуживания

Системы массового обслуживания делятся на типы (или классы) по ряду признаков.

По числу каналов СМО подразделяют на одноканальные (когда име-ется один канал обслуживания) и многоканальные, точнее n-канальные (когда количество каналов n>=2). Здесь и далее будем полагать, что каждый канал одновременно может обслуживать только одну заявку и, если не оговорено специально, каждая находящаяся под обслуживанием заявка обслуживается только одним каналом. Многоканальные СМО могут состоять из однородных каналов, либо из разнородных, отличающихся длительностью обслуживания одной заявки. Практически время обслуживания каналом одной заявки Тоб является непрерывной случайной величиной. Однако при условии абсолютной однородности поступающих заявок и каналов время обслуживания может быть и величиной постоянной (Tоб=const).

По дисциплине обслуживания СМО подразделяют на три класса:

1. СМО с отказами, в которых заявка, поступившая на вход СМО в момент, когда все каналы заняты, получает «отказ» и покидает СМО («пропадает»), Чтобы эта заявка все же была обслужена, она должна снова поступить на вход СМО и рассматриваться при этом как заявка, поступившая впервые. Примером СМО с отказами может служить работа АТС: если набранный телефонный номер (заявка, поступившая на вход) занят, то заявка получает отказ, и, чтобы дозвониться по этому номеру, следует его набрать еще раз (заявка поступает на вход как новая).

2. СМО с ожиданием (неограниченным ожиданием или очередью). В таких системах заявка, поступившая в момент занятости всех каналов, становится в очередь и ожидает освобождения канала, который примет ее к обслуживанию. Каждая заявка, поступившая на вход, в конце концов будет обслужена. Такие СМО часто встречаются в торговле, в сфере бытового и медицинского обслуживания, на предприятиях (например, обслуживание станков бригадой наладчиков).

3. СМО смешанного типа (с ограниченным ожиданием). Это такие системы, в которых на пребывание заявки в очереди накладываются некоторые ограничения.

Эти ограничения могут накладываться на длину очереди, т.е. макси-мально возможное число заявок, которые одновременно могут находиться в очереди. В качестве примера такой системы можно привести мастерскую по ремонту автомобилей, имеющую ограниченную по размерам стоянку для неисправных машин, ожидающих ремонта.

Ограничения ожидания могут касаться времени пребывания заявки в очереди, по истечению которого она выходит из очереди и покидает систему, либо касаться общего времени пребывания заявки в СМО (т.е. суммарного времени пребывания заявки в очереди и под обслуживанием).

В СМО с ожиданием и в СМО смешанного типа применяются различные схемы обслуживания заявок из очереди. Обслуживание может быть упорядоченным, когда заявки из очереди обслуживаются в порядке их поступления в систему, и неупорядоченным, при котором заявки из очереди обслуживаются в случайном порядке. Иногда применяется обслуживание с приоритетом, когда некоторые заявки из очереди считаются приоритетными и поэтому обслуживаются в первую очередь.

По ограничению потока заявок СМО делятся на замкнутые и от-крытые.

Если поток заявок ограничен и заявки, покинувшие систему, могут в нее возвращаться, то СМО является замкнутой, в противном случае — от-крытой. Классическим примером замкнутой СМО служит работа бригады наладчиков в цеху. Станки являются источниками заявок на обслуживание, и их количество ограничено, наладчики — каналы обслуживания. После проведения ремонтных работ вышедший из строя станок снова становится источником заявок на обслуживание. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО — зависят. Так, в рассмотренном выше примере интенсивность потока «заявок» со стороны станков (т.е. количество заявок в единицу времени) зависит от того, сколько их неисправно и ждет наладки.

По количеству этапов обслуживания СМО делятся на однофазные и многофазные системы.

Если каналы СМО однородны, т.е. выполняют одну и ту же операцию обслуживания, то такие СМО называются однофазными. Если каналы обслуживания расположены последовательно и они неоднородны, так как выполняют различные операции обслуживания (т.е. обслуживание состоит из нескольких последовательных этапов или фаз), то СМО называется многофазной. Примером работы многофазной СМО является обслуживание автомобилей на станции технического обслуживания (мойка, диагностирование и т.д.).

Далее будем рассматривать только однофазные СМО.

48)Игры с природой. Критерий максимального среднего выигрыша (критерий Байеса, критерий Лапласа).

Существуют игры, в которых только один игрок сознательно принимает решения(ЛПР), а другая сторона пассивна, эта сторона сознательно не принимает решения, а с некоторой вероятностью принимает какие либо состояния под влиянием случайных факторов, такого рода ситуации называют играми с природы.

Под природой понимают совокупность неопределенных факторов, влияющих на эффективность принимаемых решений активного игрока.

Существуют игры с природы, в которых известны вероятности возможных состояний, такие игры называют играми в условиях частичной неопределенности. Для выявления оптимальных стратегий активного игрока применяют критерий Байеса.

Если вероятности состояния природы неизвестны, то говорят об игре с природой в условиях полной неопределенности. Тогда для определения оптимальных стратегий активного игрока применяют критерий Лапласа, Вальда, Сэвиджа, Гурвица.

Вероятности состояния природы qj обычно определяется путем проведения экспериментов или наблюдений, поэтому их принято называть апостериорными. В качестве оптимальных стратегий по критерию Байеса принимается чистая стратегия активного игрока, при которой его средний выигрыш становится максимальным. Каждый средний выигрыш будет находится по формуле

Ai= ai1* q1+ ai2*q2+…+ ain* qn

Критерий Байеса можно рассматривать относительно средних рисков. РИСКОМ называют разность между макс выигрышем активного игрока и обозначаем max aik, который он мог бы получить достоверно зная, что природа примет состояние Пк, а также тем выигрышем, который он получит, используя стратегию Ai ( т.е., чтобы составить матрицу рисков необходимо по каждому столбцу платежной матрицы найти max элемента, а затем вычитать из него соответствующие выигрыши платежной матрицы.

rij= max aik- aik

В матрице рисков каждый столбец будет содержать хотя бы один нулевой элемент. По критерию Байеса определим средние риски активного игрока.

Ri= ri1* q1 +ri2* q2+..+rin* qn .

Оптимальной будет считаться та стратегия, при которой достигается минимальный средний риск R= min Ri.

Критерий Лапласа аналогичен критерию Байеса, но вероятности состояния природы неизвестны, поэтому предполагается, что все состояния природы равновероятны, т.е. q1=q2=…=qn=1/n

Ai=1/n (ai1 +ai2+…+ain)

Ri= 1/n( ri1+ri2+…+rin)

49. Игры с природой. Критерий Вальда. Критерий Сэвиджа. Игры с природой. Критерий Гурвица.

Существуют игры, в которых только один игрок сознательно принимает решения(ЛПР), а другая сторона пассивна, эта сторона сознательно не принимает решения, а с некоторой вероятностью принимает какие либо состояния под влиянием случайных факторов, такого рода ситуации называют играми с природы.

Под природой понимают совокупность неопределенных факторов, влияющих на эффективность принимаемых решений активного игрока.

Существуют игры с природы, в которых известны вероятности возможных состояний, такие игры называют играми в условиях частичной неопределенности. Для выявления оптимальных стратегий активного игрока применяют критерий Байеса.

Если вероятности состояния природы неизвестны, то говорят об игре с природой в условиях полной неопределенности. Тогда для определения оптимальных стратегий активного игрока применяют критерий Лапласа, Вальда, Сэвиджа, Гурвица.

Критерий Вальда- критерий крайнего пессимизма, т.к активному игроку предлагают выбрать ту стратегию, при которой наименьший выигрыш будет максимальным.

W= maxWi=max min aij

Критерий Сэвиджа- как и критерий Вальда, крайнего пессимизма, но он опирается не на исходную платежную матрицу, а матрицу рисков, значит по каждой строке нужно найти максимальный риск, а затем из всех максимальных рисков минимальный.

S=min Si=min max rij

Критерий Гурвица. Можно рассматривать критерий крайнего пессимизма (Вальда и Сэвиджа), а можно рассмотреть критерий крайнего оптимизма (максимаксные критерии), однако лучше придерживаться золотой середины.

К.Г. является критерием пессимизма-оптимизма.

В начале по каждой стратегии активного игрока рассчитывается показатель. Оптимальной по критерию Гурвица является та стратегия для которой значения Gi будет max

G=max Gi=max( min aij+ (1-) max aij)

При =1 критерий Гурвица переходит в критерий Вальда, а при получаем максимальный критерий, или критерий максимального оптимизма.

Остальные промежуточные значения  в большую или меньшую сторону смещены ими к оптимуму или пессимизму.

При желании подстраховаться  следует выбирать ближе к 1, а близкие к 0 дают более рискованный результат.

Лекция 14. Основы марковских процессов. Уравнения Колмогорова

Дата добавления: 2013-12-23 ; просмотров: 8459 ; Нарушение авторских прав

Определение марковского процесса. Пусть имеется система S, состояние которой изменяется во времени случайным, непредсказуе­мым образом и представляет собой случайный процесс. Этот процесс называется марковским, если для каждого момента времени t₀ веро­ятность любого состояния при t > t₀ (в будущем) зависит только от вероятности, состояния в момент t₀ (в настоящем) и не зависит от вероятностей состояний при t

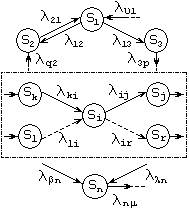
Рассмотрим некоторую произвольную систему, граф состояний которой приведен на рис.1. Система имеет n состояний S₁,S₂. S_n. Процесс перехода из одного состояния в другое описывает­ся непрерывной цепью Маркова. Пусть P_i(t) — вероятность того, что в момент времени t система будет находиться в состоянии S_i (i=1,2,…,n). Поскольку система не может находиться одновременно в двух состояниях, то события, заключающиеся в нахождении системы в состояниях S₁,S₂,…,S_n, несовместны и образуют полную сис­тему событий. Отсюда следует

(51)

Это соотношение называется условием нормировки. Задача заключает­ся в определении вероятности любого состояния P_i(t) в любой мо­мент времени t.

Введем понятие вероятности перехода системы из состояния i, где она находилась в момент времени t, в состояние j за время Dt P_ij(t,Dt). Очевидно, что P_ij(t,Dt) представляет собой условную вероятность того, что в момент времени t + Dt система окажется в состоянии S_j при условии, что в момент времени t она находилась в состоянии S_i: p_ij(t,Dt)= p(S_j(t+Dt)/S_i(t)).

Предел отношения вероятности перехода p_ij(t,Dt) к длине интервала времени Dt назовем плотностью вероятности перехода

. (52)

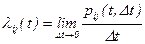
Плотность вероятности перехода определим только для случаев i¹j.

Если l_ij(t)=const, то марковская цепь называется однородной. В противном случае, когда l_ij(t) являются функциями времени, цепь называется неоднородной. При расчетах вероятностей состояний марковской цепи предполагается, что все эти плотности вероятнос­тей переходов l_ij известны. Если у каждой дуги графа состояний системы проставить плотность вероятности перехода по данной дуге, то полученный граф назовем размеченным графом состояний (см.рис.1). Уравнения Колмогорова составляются в соответствии с разме­ченным графом состояний. Рассмотрим фрагмент размеченного графа состояний (рис.1), обведенный штрихпунктирной линией. Отбро­сим вначале дуги, изображенные пунктиром, и определим вероятность нахождения системы в состоянии S_i в момент времени t+Dt. С уче­том того, что вершина S_i связана только с вершинами S_k и S_j, ука­занное событие будет иметь место в двух случаях:

— система находилась в состоянии S_i в момент времени t и за время Dt из этого состояния не вышла;

— система находилась в состояния s_k в момент времени t и за время Dt перешла из S_k в S_i.

Если отрезок Dt достаточно мал, то вероятность перехода p_ij(t,Dt) может быть определена приближенно с помощью (52)

С учетом (53) и свойства марковости процесса вероятность первого случая (отсутствие перехода по дуге (S_i,S_j))

Вероятность второго случая с учетом (53)

Тогда можно определить искомую вероятность как

(54)

Переходя в (53) к пределу при Dt ® 0, получим

. (55)

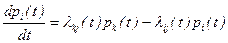
Теперь добавим к вершине Si дуги, обозначенные на рис.1 пункти­ром. Тогда при вычислении p_i(t+Dt) необходимо учитывать возможный переход из S_i в S_j и S_r и переходы из S_k и S_l в S_i. В этом случае

Повторяя вышеописанные рассуждения, получим

. (56)

На основании (55) и (56) можно сформулировать правила сос­тавления уравнений Колмогорова по размеченному графу состояний непрерывной марковской цепи:

1. Система дифференциальных уравнений Колмогорова имеет форму Коши. Каждое уравнение составляется с помощью рассмотрения ве­роятности состояния, представленного соответствующей вершиной в размеченном графе. Число уравнений системы равно числу вершин графа.

2. Число слагаемых правой части каждого уравнения равно чис­лу дуг, инцидентных соответствующей вершине.

3. Дугам с положительной инциденцией соответствуют отрица­тельные слагаемые, а дугам с отрицательной инциденцией — положи­тельные.

4. Каждое слагаемое правой части равно произведению вероят­ности состояния, соответствующего началу рассматриваемой дуги, на плотность вероятности перехода по данной дуге.

Начальные условия для системы уравнений Колмогорова опреде­ляются начальным состоянием системы. Например, если начальное состояние было S₂ , то начальные условия имеют вид: p₁(0)=0; р₂(0)=1; р₃(0)=0;…;р_n(0)=0. Уравнения (55) и (56) были вы­ведены для общего случая неоднородной марковской цепи. Для одно­родной марковской цепи все l_ij(i,j=l,…,n) постоянны.

Рассмотрим одно важное свойство уравнений Колмогорова (55), которое может быть представлено в виде

, (57)

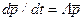
где 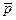— n-мерный вектор вероятностей состояний системы; р =1(t),…,p_n(t)>; L — n´n-матрица плотностей перехода.

В соответствии с вышеописанными правилами составления урав­нений Колмогорова одна и та же плотность вероятности перехода l_ij будет входить в одно из уравнений со знаком «+», а в другое — со знаком «-«, поскольку для двух смежных вершин дуга, соединяющая их, будет обладать положительной инциденцией по отношению к одной вершине и отрицательной по отношению к другой. Это приведет к то­му, что сумма всех элементов в каждом столбце матрицы будет равна нулю. Тогда любая строка матрицы L будет равна сумме остальных строк. Следовательно, матрица L является всегда вырожденной. Бо­лее строго это свойство доказывается в [7].

Рассмотрим систему с размеченным графом состояний, изобра­женным на рис.2. Система уравнений Колмогорова и матрица L для этого случая в соответствии с правилами 1-4 будут иметь вид:

Исключение любого уравнения из этой системы нарушает указанное соотношение для строк матрицы L, следовательно, ранг матрицы L будет равен n-1. Для того чтобы система уравнений Колмогорова имела единственное решение при заданных начальных условиях, не­обходимо исключить любое из уравнений системы (58) и заме­нить его условием нормировки (51).

Итак, решение системы (57) без одного уравнения (безразлич­но какого) с условием (51) определяет в любой момент времени поведение вероятностей состояний марковской цепи при заданных начальных условиях.

Получить это решение можно с помощью любых численных методов (например, Рунге-Кутта, Эйлера-Коши и т.д.), реализуемых на ЭВМ. Только в самых простых случаях система уравнений Колмогорова мо­жет быть проинтегрирована в квадратурах. В большинстве практичес­ких случаев для расчета вероятностей состояний используются не решения систем уравнений Колмогорова в любой момент времени, а асимптотические оценки этих решений при t®¥.

Лекция 15. Предельные вероятности состояний. Простейший поток событий.

Асимптотические оценки в соответствии с известной теоремой А.А.Маркова могут быть получены для марковских цепей, обладающих эргодическим свойством.

Определение 1. Если число состояний системы конечно и из каждого состояния можно перейти в любое другое за произвольное число шагов, то говорят, что такая система обладает эргодическим свойством.

Определение 2. Пусть марковский процесс характеризуется ве­роятностями перехода из состояния i в состояние j за время t

Процесс называется транзитивным, если существует такое t>0, что p_ij(t)>0 (0£i£n; 0£j£n). Из определений 1 и 2 следует, что процессы в марковских цепях с эргодическим свойством являются транзитивными.

Теорема Маркова. Для любого транзитивного марковского процесса предел 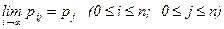существует и не зависит от начального состояния i.

Это означает, что при t®¥ в системе устанавливается неко­торый предельный стационарный режим, характеризующийся постоян­ной, не зависящей от времени, вероятностью каждого из состояний системы. При этом данная вероятность представляет собой среднее относительное время пребывания системы в данном состоянии. Это значит, что если время работы всей системы 100 ч, а вероятность состояния S1 равна p1=0,15, то система будет находиться в состоянии S1 в среднем 15 ч.

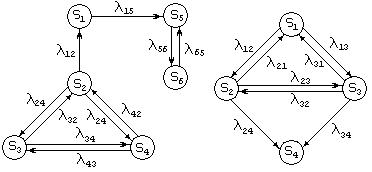
Пределы, к которым стремятся вероятности каждого из состоя­ний марковской цепи с эргодическим свойством при t®¥, называ­ются предельными вероятностями. При рассмотрении СМО мы будем иметь дело только с эргодическими марковскими цепями. Пусть V — некоторое подмножество множества состояний системы S , а V’ — его дополнение до S . Если множество V обладает эргодическим свойс­твом и ни из одного состояния множества V нельзя перейти ни в од­но из состояний множества V’, то множество называется замкнутым или эргодическим множеством. Эргодические системы состоят из од­ного единственного эргодического множества (S=V, V’=Æ) и называются поэтому неразложимыми. Если в системе S множество V’¹Æ или в этой системе можно выделить несколько эргодических множеств S = V₁ÈV₂È…ÈV_n, то такая система называется разложимой. Примеры таких систем приведены на рис.3.

На рис.3,а представлена сис­тема с двумя эргодическими множест­вами V₁=(S₂,S₃,S₄) и V₂(S₅,S₆). На рис.3, б эргодическое множество состоит лишь из одного состояния (S₄). Если эргодическое множест­во состоит лишь из одного состоя­ния, то это состояние называется поглощающим, так как попав в не­го однажды, процесс остается нав­сегда в поглощающем состоянии. Ха­рактерная особенность графа состо­яний неразложимой эргодической мар­ковской системы заключается в том, что каждой вершине этого графа ин­цидентны дуги как с положительной, так и с отрицательной инцидент­ностью (т.е. у каждой вершины име­ются дуги, направленные как к вер­шине, так и от нее, см., например, рис. 1 и 2).

Вычисление предельных вероят­ностей состояний для таких систем упрощается в связи с тем, что, поскольку все эти вероятности яв­ляются постоянными величинами, то их производные по времени рав­ны 0 (dp_i/dt=0 для всех i). Поэтому левые части системы уравнений Колмогорова (58) приравниваются нулю и она превращается в систе­му линейных алгебраических уравнений

. (59)

Нетривиальное решение системы (59) может быть получено только в случае вырожденности матрицы L. Выше было доказано, что матрица плотностей вероятностей L является вырожденной. Система (59) без одного из своих уравнений дополняется условием нормировки

(60)

Соотношения (59) и (60) позволяют определить предельные вероят­ности состояний. Поскольку часть слагаемых, соответствующая дугам с отрицательной инцидентностью, положительна, а другая часть, со­ответствующая дугам с положительной инцидентностью, отрицательна, то каждое уравнение системы (59) может быть составлено с учетом мнемонического правила: для каждого состояния сумма членов, соот­ветствующих входящим дугам, равна сумме членов, соответствующих выходящим дугам.

Пример. Для системы, изображенной на рис.2, из уравнений Колмогорова (58) следует

Для решения (61) нужно исключить любое из первых пяти уравнений (например, пятое, как содержащее наибольшее число членов).

Предельные вероятности состояний используются в ТМО значи­тельно чаще, чем решения уравнений Колмогорова, причем, зная ре­шение системы уравнений Колмогорова, можно определить момент окончания переходного процесса изменения вероятностей состояний во времени. Это дает возможность рассчитать, промежуток времени начиная от включения системы в работу, по истечении которого ве­роятности состояний достигнут своих предельных значений и будут справедливы оценки, использующие эти значения. В заключение этого параграфа рассмотрим один частный, но практически очень важный класс марковских процессов, широко применяемых при исследовании СМО. Это — процессы «размножения и гибели». К ним относятся мар­ковские цепи, представимые размеченным графом, который состоит из вытянутой цепочки состояний, изображенной на рис.4.

Матрица плотностей вероятностей переходов такой системы яв­ляется якобиевой (тридиагональной):

Рассматривая начальное состояние S₀ , получим в соответствии с (59)

Для состояния S₁ имеем

Вычитая из (63) равенство (62), получим

Продолжая этот процесс до n-гo состояния включительно, получим

Из (62) теперь можно выразить p₁ через р₀:

Подставляя (64) в (65), получим

Очевидно, что для произвольного k (1£k£n) будет справедливо вы­ражение

. (66)

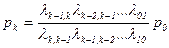
В соответствии с (66) и размеченным графом состояний, представленным на рис.4, можно сформулировать правило, с по­мощью которого можно выразить предельные вероятности состояний процесса «размножения и гибели» через вероятность начального сос­тояния р₀. Это правило гласит: вероятность произвольного состоя­ния p_k (l£k£n) равна вероятности начального состояния р₀, умно­женной на дробь, числитель которой равен произведению плотностей вероятностей перехода для дуг, переводящих состояние системы сле­ва направо, а знаменатель — произведение плотностей вероятностей перехода справа налево от начального до k-гo состояний включи­тельно.

Вероятность р₀ находится из условия нормировки и выражений (66) следующим образом:

(67)

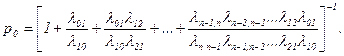
Выражения (66) и (67) полностью определяют предельные вероят­ности процесса «размножения и гибели».

Цепи Маркова с непрерывным временем являются математическими моделями СМО. Для анализа СМО необходимо также иметь математичес­кие модели входных потоков заявок на обслуживание. Эти математи­ческие модели представляют собой потоки события, являющиеся от­дельным классом случайных процессов. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени. Этот поток количественно может быть охарактеризован числом событий x(t), имевших место в течение определенного промежутка времени (0,t). Тогда случайный поток со­бытий можно определить как случайный процесс x(t) (t³0), в кото­ром функция x(t) является неубывающей функцией времени, способной принимать лишь целые неотрицательные значения. Иными словами, график функции x(t) является ступенчатой кривой с постоянной вы­сотой ступеньки, равной единице, причем ширина ступеньки — слу­чайная величина. Примерами таких потоков могут служить: поток вызовов на АТС, поток запросов в вычислительный центр коллективного пользования и т.п. Моменты появления событий можно отобразить точками на временной оси, поэтому поток событий часто представляется и как последовательность таких точек. Поток событий называется регулярным, если события следуют одно за другим через одинаковые, строго фиксированные промежутки времени.

В ТМО такие потоки практи­чески, не используются, однако они представляют интерес как предельный случай. Значительно чаще имеют дело с потоками, в которых времена поступления со­бытий и, следовательно, проме­жутки времени между ними являются случайными (иррегулярными). При этом наиболее простые рас­четные соотношения получаются при использовании простейших потоков событий, которые широко применяются при исследовании CMО.

Простейшими называются потоки, обладающие следующими тремя свойствами: стационарностью, ординарностью и отсутствием последействия. Рассмотрим эти свойства подробнее.

1. Поток событий называется стационарным, если вероятность p_k(l) того, что за отрезок времени t произойдет k событий, зави­сит только от его длины t и не зависит от его расположения на временной оси, т.е. p_k(t’,t’+t)=p_k(t). Из определения однородной марковской цепи следует, что стационар­ность — это однородность потока по времени.

2. Поток называется ординарным, если вероятность попадания на любой элементарный участок временной оси двух или более собы­тий является бесконечно малой величиной, т.е.

3. Поток событий называется потоком без последействия, если вероятность попадания событий на некоторый участок временной оси не зависит от того, сколько событий попало на другие участки. Иными словами, условная вероятность наступления k событий за про­межуток времени (t’,t’+t), вычисленная при любом условии чередо­вания событий до момента t’, равна безусловной вероятности p_k(t) того же события, т.е.

p[(t’,t’+t),k/(t»,t»+t),m]=p_k(t),tÇt_k=Æ, t» T), т.е. вероятность того, что случайная величина Т при­мет значение, меньшее чем t. Для этого необходимо определить ве­роятность того, что в интервал времени t, отсчитываемый от момента t₀ появления некоторого события, попадет еще хотя бы одно событие (см.рис.5,б). Эту вероятность можно определить, зная вероятность отсутствия событий в интервале t, равную вероятности p₀(t) состояния S₀ на графе рис.5, а. В соответствии с (72)

F(t)=p(t>T)=1-e — l t , t>0 . (73)

Дифференцируя (73) по времени, получим искомый закон распреде­ления

(74)

Закон распределения (74) называется показательным (экспоненци­альным). Определим первые два момента показательного распределе­ния:

(75)

(76)

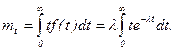
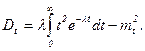
Интегрируя (75) и (76) по частям, получим

. (77)

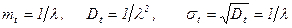
Из (77) следует, что для показательного распределения математи­ческое ожидание и среднеквадратичное отклонение равны друг другу. Кроме того из (77) следует, что в простейшем потоке среднее время между двумя соседними событиями равно обратной величине ин­тенсивности потока.

Определим теперь вероятность попадания одного события в простейшем потоке на элементарный участок временной оси (см.рис.5,б). Так же, как и в предыдущем случае, эта вероятность

Разлагая e — l D t в ряд по степеням lDt и ограничиваясь только первой степенью (в силу малости Dt), получим

Выражение в правой части (78) называется элементом вероятности появления события в простейшем потоке.

Марковские цепи являются математи­ческими моделями некоторых реальных систем, а потоки событий яв­ляются моделями внешних воздействий на эти системы. В дальнейшем будем считать, что переход системы из одного состояния i в другое j в соответствии с размеченным графом состояний происходит под действием потока событий с интенсивностью l_ij, равной соответс­твующей плотности вероятности перехода. Эта интенсивность определяется как среднее число переходов из состояния i в состояние j за единицу времени.

Если все потоки событий являются пуассоновскими, то процесс в системе будет марковским.

Лекция 16. Модели систем массового обслуживания при пуассоновских потоках заявок. Модели систем массового обслуживания с отказами

Рассмотрим сначала самую простую одноканальную СМО с отказа­ми. Поток заявок, приходящих на вход данной СМО, обслуживается одним прибором. Если прибор занят, то заявка получает отказ и по­кидает систему. В качестве примера можно привести местную теле­фонную станцию с одним каналом выхода в городскую сеть. Размечен­ный граф состояний такой системы изображен на рис. 6.

Здесь S₀ — состояние, при котором обслуживающий прибор свободен, S₁ — состояние, при котором он занят. Вправо (из состояния S₀ в состояние S₁) систему переводит поток заявок с интенсивностью l, а влево — поток обслуживания с интенсивностью m. Будем считать, что оба потока являются пуассоновскими. Тогда время обслуживания является случайной величиной, распределенной по показательному закону с математическим ожиданием Т_об = l/m. Необходимо определить абсолютную и относительную пропускные способности данной СМО.

Относительная пропускная способность q может быть оценена как вероятность того, что заявка, пришедшая в СМО, будет обслужена. Очевидно, что это будет вероятность р₀ состояния S₀. Абсолютная пропускная способность А может быть оценена как произ­ведение относительной пропускной способности q на среднее число всех заявок в единицу времени l

Таким образом, чтобы определить все характеристики данной СМО. необходимо знать вероятности состояний р₁ и р₀. Воспользуемся для этого уравнениями Колмогорова. В соответствии с вышеизложенными правилами и свойством вырожденности матриц плотностей вероятнос­тей перехода достаточно написать уравнение для вероятности состояния р₁ и условие нормировки

(80)

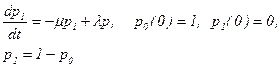
Начальные условия уравнения (80) означают, что в момент запуска СМО обслуживающий прибор свободен. Подставляя (81) в (80) и решая полученное уравнение при данных начальных условиях, будем иметь:

очевидно, что в соответствии с (77) вероятность

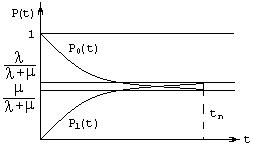
Графики функций p₀(t) и p₁(t) представлены на рис.6, видно, что при t®¥ вероятности р₀ и p₁ асимптотически стремятся к постоянным значениям. Изменение во времени вероят­ностей состояний называется переходным процессом (аналогично переходным процес­сам в динамических систе­мах). Количественная оценка характеристик СМО, основан­ная на установившихся (пре­дельных) вероятностях состояний, справедлива только лишь для моментов времени t>t_n, где t_n — время переходного процесса, начиная с которого вероятности состояний будут отличаться от своих предельных значений на достаточно малую величину. Это время t_n можно легко оценить с помощью показателя экспоненты -(l+m).

Изложенное дает основание заключить, что установившиеся зна­чения относительной и абсолютной, пропускных способностей данной СМО равны соответственно

(82)

(83)

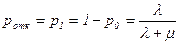
Ранее отмечалось, что вероятности состояний могут быть определе­ны как средние времена нахождения системы в этих состояниях. Ес­ли 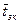— среднее время занятости канала (среднее время нахождения заявки в СМО), а — среднее время простоя канала, то вероят­ность равна

Таким образом, зная предельные вероятности состояний, можно определить все характеристики СМО.

Перейдем теперь к более сложной системе — многоканальной системе массового обслуживания с отказами, которая называется системой Эрланга. Размеченный граф состояний СМО Эрланга пред­ставлен на рис.8, где S₀ — состояние СМО, при котором все ка­налы свободны; S₁ — один канал занят, остальные свободны; S₂ — два канала заняты, остальные свободны; S_n — все n каналов заняты.

На вход системы поступает поток заявок с интенсивностью l, кото­рый будем полагать пуассоновским. Очевидно, что этот поток пере­водит систему вправо, поскольку с приходом каждой заявки занима­ются свободные каналы. С другой стороны, на систему от каждого прибора действуют потоки обслуживания, которые также будем пред­полагать пуассоновскими с одинаковой интенсивностью m, так как все каналы одинаковы. Очевидно, что если работают одновременно два прибора, то интенсивность суммарного потока обслуживания бу­дет равна 2/m, а если работают все n каналов, то интенсивность суммарного потока обслуживаний будет равна nm. Поэтому интенсивности потоков, переводя­щих систему влево, возрастают с увеличением номера состояния.

Задача Эрланга заключается в нахождении вероятностей всех состояний данной СМО и вычислении по ним ее характеристик.

В соответствии с размеченным графом состояний система урав­нений Колмогорова будет иметь вид

с начальными условиями: р₀(0)=1, p_k(0)=0 (k=1,…,n), кото­рые соответствуют случаю, когда все каналы свободны при t=0. При этом решение (80) должно удовлетворять условию

Уравнения (84) называются уравнениями Эрланга. В общем случае интегрирование системы уравнений Эрланга выполняется с помощью численных методов, реализуемых на ЭВМ, так как аналитическое ре­шение является слишком сложным. Поэтому в дальнейшем ограни­чимся определением вероятностей состояний для установившегося ре­жима.

В соответствии с правилами определения предельных вероятнос­тей состояний процесса размножения и гибели с размеченным графом состояний, изображенным на рис.8, запи­шем выражения для предельных вероятностей состояний:

(85)

Введем безразмерный параметр r=l/m и назовем его приведенной интенсивностью потока заявок, равной среднему числу заявок, по­ступивших за среднее время обслуживания (Т_ОБ=1/m). Тогда форму­лы (85) можно представить в виде

(86)

Формулы (86) называются формулами Эрланга.

Формулы Эрланга можно выразить через табличные функции рас­пределения Пуассона

(87)

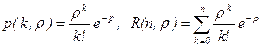
аналогичные дифференциальному и интегральному законам распределе­ния. Так же, как и для нормального распределения, таблицы этих функций имеются в литературе. С учетом (87) формулы Эрланга (86) перепишутся в виде

Определив вероятности состояний, перейдем к вычислению характе­ристик СМО Эрланга.

1) Вероятность отказа будет равна вероятности р_n состояния S_n, когда все каналы заняты:

(88)

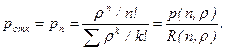
2) Вероятность того, что поступившая заявка будет принята к обслуживанию, является оценкой относительной пропускной способ­ности q:

(89)

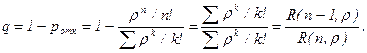
3) Абсолютная пропускная способность в соответствии с (75)

(90)

4) Среднее число занятых каналов может быть определено по формуле для расчета математического ожидания случайной величины k, принимающей целочисленные значения с вероятностями p_k:

(91)

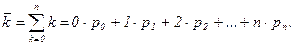
Однако в данном случае можно обойтись более простой формулой. Среднее число А заявок, обслуженных в единицу времени, будет рав­но среднему числу занятых каналов k, умноженному на интенсивность потока обслуживания каждого канала m, т.е. А=km, откуда

(92)

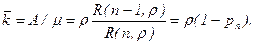
Отсюда коэффициент загрузки системы будет равен

(93)

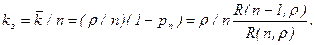
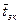
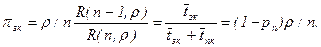
5) Определим коэффициент загрузки через вероятность занятос­ти канала — p_ЗК. Эту вероятность можно выразить через среднее время занятости канала и среднее время простоя

(94)

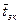
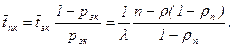
Среднее время занятости канала равно, очевидно, среднему времени обслуживания одной заявки = 1/m. Следовательно, среднее время простоя канала можно найти из выражения (94)

(95)

Формулы (88) – (95) позволяют рассчитывать характеристики СМО как с применением функций P(k,r) и R(n,r), так и без них.

6) Дисперсия числа занятых каналов будет равна

Лекция 17. Модель простейшей одноканальной системы массового обслуживания с очередями.

Рассмотрим вначале простейшую одноканальную СМО с очередью, число мест в которой ограничено числом m (рис. 9). В системе возможны такие состояния: S₀— прибор свободен, очереди нет; S₁ -прибор занят, очереди нет; S₂ — прибор занят, в очереди стоит од­на заявка; S₃ — прибор занят, в очереди стоят две заявки; … ; S_m+1 — прибор занят, в очереди стоят m заявок.

Если заявка приходит в момент времени, когда система нахо­дится в состоянии S_m+1, то она получает отказ и покидает систему. Поскольку работает только один прибор, то интенсивность потока обслуживаний m одинакова для всех состояний. Используя правила вычислений вероятностей состояний для данного процесса размноже­ния и гибели, получим

. (96)

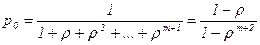
В формуле (96) использован тот факт, что знаменатель является суммой членов геометрической прогрессии со знаменателем r. С по­мощью (96) можно рассчитать основные характеристики системы.

1. Вероятность отказа в соответствии с правилами работы сис­темы равна вероятности последнего состояния p_m+1:

.

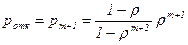
2. Относительная пропускная способность

(97)

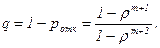
3. Абсолютная пропускная способность

4. Среднее число заявок, находящихся в очереди (математи­ческое ожидание количества заявок), определяется путем суммирова­ния всех возможных длин очередей от 1 до m с их вероятностями в качестве весовых коэффициентов:

(98)

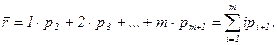
Подставляя в (98) значения вероятностей из (96), получим

(99)

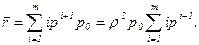
Для вычисления суммы в (99) воспользуемся методом дифференциро­вания рядов с учетом формулы суммы геометрической прогрессии со знаменателем r:

(100)

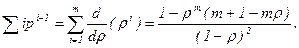
Следовательно, подставляя (100) и (96) в (99), получим

(101)

5. Среднее число заявок, находящихся в системе:

где W — случайная величина, принимающая значения 0 (канал свобо­ден) и 1 (канал занят). Вероятность занятости канала (с учетом (97))

(102)

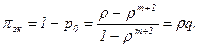
Следовательно, M[W] = 0×p₀+l(l-p₀)=rq, откуда

6. Среднее время ожидания заявки в очереди можно определить, усредняя времена ожидания заявок в очереди по всем состояниям S₁ + S_m+1, с учетом вероятностей этих состояний. Поскольку среднее время обслуживания одной заявки равно l/m, то среднее время ожидания заявки в очереди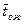

Подставляя сюда выражение для p₁ из (92) и принимая во внимание формулу (96), имеем:

(103)

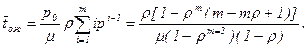
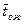
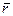
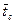
Сравнивая (103) и (97), получим = /l. Таким образом, среднее время ожидания заявки в очереди равно среднему числу зая­вок в очереди, деленному на интенсивность потока заявок. Среднее время нахождения заявки в системе определяется аналогичным об­разом:

7. Среднее время простоя канала t_ПК, в соответствии с (91) равно:

где среднее время занятости 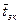= 1/m, а p_ЗК определяется из (102). Тогда

Рассмотрим теперь предельный случай, когда число мест в очереди не ограничено (m®¥). Этот случай имеет смысл только при r 0, то Sr_i=¥ и для любого конечного k

Это означает, что для любого k система рано или поздно пройдет состояние sК и никогда в него не вернется, двигаясь все время вправо по графу процесса «размножения и гибели», т.е. очередь бу­дет разрастаться до бесконечности. Иными словами, если l³m, то система при бесконечной длине очереди не справляется с потоком заявок. Поэтому, когда m=¥ мы будем рассматривать только слу­чай r n æp₀/n!

(109)

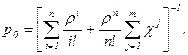
Просуммируем геометрическую прогрессию со знаменателем æ в выражении для р₀. Получим

. (110)

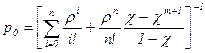
Выражения (109) и (110) дают возможность по аналогии с одноканальной СМО определить все основные характеристики многоканальной СМО:

1. Вероятность отказа

2. Относительная пропускная способность

q = 1 — p_ОТК = 1 — r n æ m p₀/n!

3. Абсолютная пропускная способность

А = lq = l[1 — r n æ m p₀/n!]

4. Среднее число заявок в очереди

5. Среднее число занятых каналов . Если каждый канал об­служивает в среднем m заявок в единицу времени, а вся СМО обслу­живает А заявок за то же время, то среднее число занятых каналов

(111)

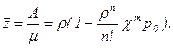
Отсюда можно определить вероятность занятости канала p_ЗК = /n.

6. Среднее число заявок, находящихся в системе,.

7. Среднее время ожидания заявки в очереди.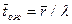

8. Среднее время ожидания заявки в системе.

Перейдем к предельному случаю при m®¥. Легко заметить, что этот переход возможен, как и в предыдущей СМО, только при æ 1 /1! (i=1,…,n)

2. Вероятность отказа Р_ОТК = 0, q = 1, A = l.

3. Среднее число заявок в очереди

(113)

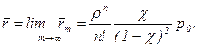
4. Среднее число занятых каналов z и среднее число заявок k, находящихся в системе:

(114)

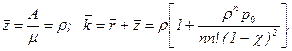
Остальные характеристики находятся аналогичным образом.

В заключение рассмотрим СМО с ограниченным временем пребывания заявки в очереди. Будем считать, что число мест в очереди не ограничено (m=¥), а число каналов обслуживания равно n. Раз­меченный граф состояний такой системы представлен на рис.11, где состояния S₀ + S_n+r имеют тот же смысл, что и в предыдущем случае. Различие заключается в том, что заявки могут находиться в очереди ограниченное время, после чего они покидают систему, если за время ожидания их не успеют обслужить. Для того чтобы рассмот­реть такую СМО с «нетерпеливыми» заявками в рамках теории марковских процессов, будем считать, что на заявки, стоящие в очере­ди, действует пуассоновский «поток уходов» с интенсивностью v. Если среднее время ожидания заявки в очереди равно 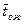, то

Тогда интенсивности потоков, переводящих состояние системы влево, равны сумме интенсивности потока обслуживании nm и соответствую­щих интенсивностей потоков уходов rv = r/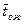, где r — число зая­вок, находящихся в очереди. Кроме приведенной интенсивности пото­ка заявок æ = l/nm введем также приведенную интенсивность потока уходов многоканальной СМО b = v/nm.

Тогда в соответствии с правилами вычисления вероятностей состоя­ний процесса размножения и гибели получим:

(115)

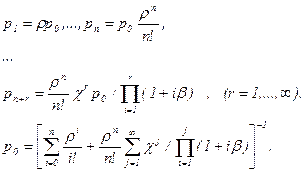
Бесконечный ряд в выражении для р0 сходится при любых æ и b. В этом можно убедиться, применяя любой известный признак сходимости рядов. Это означает, что поток уходов стабилизирует очередь и не позволяет ей разрастись до бесконечности. Среднее число заявок, находящихся в очереди такой СМО, можно определить обычным обра­зом:

Однако такой способ весьма затруднителен, так как требует вначале подсчета суммы членов бесконечного ряда в формуле (111), а затем необходимо снова определять сумму членов уже другого бесконечного ряда для нахождения среднего значения r. Это затруднение можно обойти следующим образом.

Определим вначале абсолютную пропускную способность. Если в очереди содержатся в среднем r заявок, то в единицу времени будет уходить vr заявок, а приходить — l заявок. Оставшиеся после ухо­дов заявки будут обслужены, следовательно.

А = l — v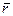. (116)

Относительная пропускная способность

(117)

Среднее число занятых каналов определяется аналогично предыдущему случаю:

(118)

Из (118) можно найти r:

(119)

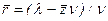
Таким образом, среднее число заявок в очереди мы выразили через среднее число занятых каналов. Эта величина, очевидно, получается в результате суммирования конечного ряда

Однако сумму этого ряда определить достаточно сложно из-за необходимости суммирования бесконечного ряда для нахождения рn. Чтобы обойти это затруднение, сумму членов бесконечного ряда заменя­ют суммой (r-1) членов конечного ряда, отбрасывая все остальные члены, начиная с r-го. Легко показать, что погрешность вычисления суммы в результате такой замены

.

Заметим, что из (115) — (119) при v®0 (или b®0) в пределе получаем выражения для обычной многоканальной СМО с очередью («нетерпеливые» заявки становятся «терпеливыми»). Вероятность от­каза в такой СМО с «нетерпеливыми» заявками не имеет смысла.

Все прочие характеристики СМО находятся способом, аналогичным ранее описанному.