Записать уравнение траектории движения материальной точки

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

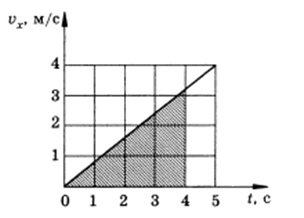
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Траектория движения

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

• прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
• и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Уравнение траектории движения

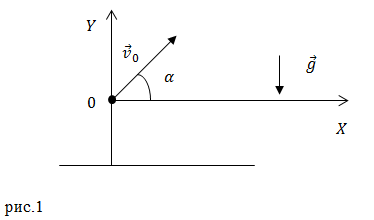
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($\frac$) от нее по $x$.

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t\ $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

• Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=\rho ,x_2=\varphi ,x_3=\ z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: \[x_1=x_1\left(t\right);;\ x_2=x_2\left(t\right);;\ x_3=x_3\left(t\right)\left(6\right).\]
• При описании движения в векторной форме положение материальной точки задает радиус-вектор ($\overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $\overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: \[\overline=\overline\left(t\right)\left(7\right).\]
• Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $\overline=A\overline+Bx\overline\ ,\ $где $\overline$, $\overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. \textit<>

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $\left\< \begin x=At. \\ y=At(1+Bt) \end \right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

Уравнение движения материальной точки

Вы будете перенаправлены на Автор24

Система отсчета. Системы координат

Под движением материальной точки в пространстве понимают изменение ее положения относительно некоторых тел с течением времени. В связи с этим можно говорить только о движении в некоторой системе отсчета.

Сами по себе точки пустого пространства неразличимы между собой, поэтому говорить о той или иной точке пространства можно, если в ней находится материальная точка. Ее положение и определяется относительно тела отсчета с помощью измерений, для чего с телом (телами) отсчета жестко связывается некоторая система координат; в ней и измеряются пространственные координаты. Например, на поверхности Земли это географическая широта и долгота точки.

В теоретических рассуждениях часто наиболее удобна декартова прямоугольная система координат, в которой положение точки определяется радиус-вектором $\overline$ с тремя проекциями $x,y,z$ — координатами точки. Но возможно и использование других систем координат, например:

• сферической, где положение точки и ее радиус-вектор определены координатами $r,\vartheta ,\varphi $;
• цилиндрической: с координатами $p,z,\alpha $;
• на плоскости — полярной: $r,\varphi $.

В теоретических рассуждениях часто не принимают во внимание реальную систему отсчета, сохраняя только систему координат, которая и служит математической моделью системы отсчета, применяемой при измерениях на практике.

Кинематическое уравнение движения материальной точки

Итак, в любой системе отсчета и системе координат имеется возможность определить координаты материальной точки в любой момент времени.

Если положение материальной точки в каждый момент времени определено в данной системе отсчета, то движение ее задано или описано.

Это задание достигается в виде кинематического уравнения движения:

Аналитически положение точки всегда определяется совокупностью трех независимых между собой чисел. Этот факт выражают словами: свободная точка имеет три степени свободы движения.

Готовые работы на аналогичную тему

Движение точки согласно уравнению (1) полностью определено, если указано ее положение в любой момент времени $t$. Для этого достаточно задать декартовы координаты точки как однозначные и непрерывные функции времени:

Прямоугольные декартовы координаты $x,y,z$ являются проекциями радиус-вектора $\overline$, проведенного в точку из начала координат, т.е.:

Длина и направление вектора $\overline$находятся из известных соотношений:

Здесь, $\alpha ,\beta ,\gamma $ — углы, образованные радиус-вектором с координатными осями.

Равенства (2) являются кинематическими уравнениями движения материальной точки в декартовых координатах. Но уравнения могут быть записаны в любой другой системе координат, связанной с декартовой взаимно однозначным преобразованием. При движении точки в плоскости Оху часто бывает удобно пользоваться полярными коордиинатами $r,\varphi $, связанными с декартовыми преобразованием:

В этом случае кинематические уравнения движения точки имеют следующий общий вид:

$r=r(t),\varphi =\varphi (t)$. (3)

В криволинейных координатах $q_ <1>,q_ <2>,q_ <3>$ связанных с декартовыми преобразованием:

кинематические уравнения движения точки запишутся так:

(Это могут быть сферические, цилиндрические и другие координаты).

Годограф радиус-вектора точки, т.е. кривая, описываемая концом вектора $\overline$при движении точки, совпадает с траекторией движения этой точки. Уравнение траектории в параметрической форме, когда параметром служит время $t$, дано кинематическими уравнениями движения (2), (5). Для получения уравнения траектории в координатной форме достаточно исключить из кинематических уравнений время.

Движение точки может быть определено по-другому: заданием траектории и мгновенным положением точки на ней. Положение точки на кривой определяется указанием только одной величины — расстояния, измеряемого вдоль кривой от некоторой начальной точки. При этом должно быть указано положительное направление кривой. Тогда мгновенное положение точки на заданной кривой определяется функцией:

Это уравнение является уравнением движения точки по траектории. Такой способ задания движения называется естественным или траекторным.

Координатный и естественный способы задания движения точки физически (в смысле фиксации ее положения в пространстве)

эквивалентны. Что же касается математической стороны дела, то в одних задачах оказывается проще применение координатного, а в другом — естественного метода.

Закон движения точки по траектории может быть задан аналитически, графически или в виде таблицы. Оба последних способа широко применяются на транспорте (например, графики и расписания движения поездов).

Уравнение движения материальной точки имеет вид $x=0,4t^ <2>$. Написать формулу зависимости $v_ (t)$ и построить график зависимости скорости точки от времени. Показать на графике площадь, численно равную пути, пройденному точкой за 4 секунды, и вычислить этот путь. \end

Решение: Зависимость скорости от времени имеет вид:

Запишем уравнение зависимости координаты от времени и сравним его с данным:

Из сравнения видно, что $x_ <0>=0$, $v_ <0x>=0$, $a_ =0,8$м/с2.

Подставим полученные данные в уравнение скорости и получим:

Определим точки и построим график:

Путь, пройденный телом, численно равный площади фигуры, ограниченной графиком и может быть найден по следующей формуле:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 07 2021