Записать уравнение вынужденных колебаний малой частоты

§ 1.9. Вынужденные колебания

Наиболее простой способ возбуждения незатухающих колебаний состоит в том, что на систему действует внешняя периодическая сила. Колебания под действием внепхней периодической силы называются выну веденными. Работа этой силы над системой обеспечивает приток энергии к системе извне, который и не дает колебаниям затухать, несмотря на действие сил трения.

Под влиянием периодической силы любое тело или система совершает колебания. Но если система сама по себе не способна соверпхать колебания, то ничего интересного в ней под действием периодической силы не произойдет. Вспомните пример с книгой, которую можно двигать рукой по столу слева направо и справа налево.

Если же система способна соверпхать свободные колебания, то действие на нее периодической внепхней силы вызывает весьма интересные и практически важные явления. С ними знакомы все, кому приходилось раскачивать ребенка на качелях.

Качели — это маятник, обладающий определенной собственной частотой. Значительно отклонить качели от положения равновесия трудно. Постоянная во времени сила здесь мало эффективна. Не раскачает качели взрослый человек и в том случае, если он будет их беспорядочно подталкивать в разные стороны. Однако, если начать работать в правильном ритме, подталкивая качели вперед каждый раз, когда они поравняются с нами, можно без больших усилий раскачать их очень сильно. Правда, для этого потребуется некоторое время*.

Раскачать качели до больших амплитуд можно только под действием такой периодической внепхней силы, которая изменяется с частотой, равной частоте свободных колебаний качелей (маятника).

Вот эта возможность резкого увеличения амплитуды колебаний маятника или любой другой системы, способной совершать свободные колебания, при совпадении частоты внешней силы с собственной частотой колебательной системы и представляет главный интерес.

Наблюдение вынужденных колебаний

Давайте подробнее познакомимся с вынужденными колебаниями системы, обладающей собственной частотой колебаний. Рассмотрим вместо маятника груз, подвешенный на пружине. Но теперь верхний конец пружины будет прикреплен к «колену» изогнутой оси (рис. 1.16). Если вращать ось с помощью рукоятки, то на груз, прикрепленный к пружине, начнет действовать периодическая внешняя сила. Еще лучше вращать ось с помощью электродвигателя. Это обеспечит большую стабильность частоты внешней силы.

Постепенно груз начнет раскачиваться. Амплитуда его колебаний нарастает. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда со временем перестанет изменяться. Присмотревшись внимательно, вы обнаружите, что частота колебаний груза будет в точности равна частоте колебаний точки подвеса пружины, т. е. частоте изменения внешней силы. (Эта частота равна угловой скорости вращения рукоятки.) В этом ничего неожиданного нет. Если толкать груз вверх и вниз, то он в конце концов начнет качаться с той же частотой, с которой вы действуете на него.

Установление колебаний

Но почему с течением времени устанавливается определенная амплитуда колебаний? Проще всего это можно понять, исходя из энергетических соображений. Внешняя сила совершает за период работу А₁, которая, конечно, прямо пропорциональна амплитуде колебаний (рис. 1.17, график 1). Ведь работа всегда пропорциональна пройденному пути. За счет этой работы увеличивается энергия колеблющегося тела и, следовательно, размах колебаний.

Одновременно с ростом амплитуды колебаний растут потери механической энергии в системе. Силы трения за период совершают работу А₂. При этом от системы отбирается механическая энергия. Работа сил сопротивления также пропорциональна амплитуде, так как с увеличением амплитуды растет пройденный телом путь. Но нужно еще учесть, что сама сила сопротивления, если считать ее прямо пропорциональной скорости (_с = -k₁), растет пропорционально амплитуде. Ведь чем больше амплитуда колебаний, тем быстрее при заданном периоде движется колеблющееся тело. В результате работа А₂ оказывается пропорциональной квадрату амплитуды (рис. 1.17, график 2).

При раскачке колебаний, когда амплитуда еще мала, |А₂| ОВ). Разумеется, при этом требуется и большее время для того, чтобы колебания установились.

Установившиеся вынужденные колебания происходят с частотой ω и амплитудой х_m по гармоническому закону:

Внешне вынужденные установившиеся колебания выглядят так же, как и свободные колебания в системе без трения. Но если при свободных колебаниях амплитуда х_m и начальная фаза фо определяются начальными условиями, то при вынужденных колебаниях х_m и φ_c определяются (как мы увидим в дальнейшем) параметрами самой системы и внешней силой. Прежде всего играет существенную роль соотношение частот собственных и вынужденных колебаний. Величина φ_c в случае вынужденных колебаний — это не начальная фаза, а сдвиг фаз между колебаниями координаты и внешней силы. Скорость и ускорение при вынужденных колебаниях определяются такими же уравнениями, как и при свободных колебаниях:

Уравнение движения для вынужденных колебаний

Приступим к репгению основной задачи: выясним, от чего и как зависят амплитуда х_m вынужденных колебаний и сдвиг фаз φ_c. Для этого запишем и исследуем уравнение движения для вынужденных колебаний.

Пусть на колебательную систему (груз на пружине) действует внешняя периодическая сила F_x = F_m cos ωt. Кроме того, на тело действует сила упругости (F_у)_х = -kx и сила сопротивления, пропорциональная скорости: (F_c)_х = -k₁v_х, где k₁ — коэффициент сопротивления. (При малых скоростях движения тела силу сопротивления можно считать пропорциональной скорости.) Тогда уравнение движения запишется так:

Перенеся в левую часть уравнения все силы, кроме внешней, получим:

Удобнее записать это уравнение в несколько другом виде, разделив правую и левую его части на то и введя собственную частоту :

Движение тела, подчиняющееся этому уравнению, достаточно сложно, особенно вначале, когда оно не является гармоническим. Мы рассмотрим лишь три предельных случая.

Первый случай: ,т. е. частота внешней периодической силы много меньше частоты собственных колебаний системы.

Второй случай: ω >> ω₀; выполняется противоположное условие.

И наконец, самый важный случай: ω = ω₀**. Это случай резонанса.

Вынужденные колебания малой частоты

Если ω 2 x_m, второго — ωx_m, а последнего — x_m. Поэтому приближенно (учитывая, что ω ⇒ 0) имеем:

Колебания координаты происходят с амплитудой , а фаза колебаний совпадает с фазой колебаний внешней силы. Отметим, что амплитуда колебаний тем меньше, чем больше жесткость пружины. Качественно этот случай можно описать так. При малой частоте изменения внешней силы происходит почти то же самое, что и при действии на пружину постоянной силы. В соответствии с законом Гука смещение увеличивается пропорционально внешней силе, и в любой момент внешняя сила почти точно уравновешивается силой упругости пружины.

С энергетической точки зрения условия для перекачки энергии в колебательную систему от внешних тел, действующих на систему с период ич*еской силой, в данном случае очень неблагоприятны. В самом деле: четверть периода, когда тело смещается от положения равновесия, внешняя сила совершает положительную работу, так как сила и скорость тела, а значит, и перемещение направлены в одну сторону (рис. 1.19, а). Но в следующую четверть периода, когда тело возвращается к положению равновесия, сила и скорость (а значит, и перемещение) направлены в противоположные стороны (рис. 1.19, б). Работа внешней силы при этом отрицательна. Та же картина будет наблюдаться во вторую половину периода. В целом за период работа внешней силы почти точно равна нулю. Лишь малая часть работы внешней силы идет на компенсацию работы силы трения, так как скорость движения тела при ω > ω₀ в левой части уравнения (1.9.5) наибольшим будет первый член, амплитуда которого пропорциональна квадрату частоты. Он играет основную роль и поэтому можно записать

По фазе с колебаниями силы совпадают теперь не колебания координаты, а колебания ускорения. Колебания координаты происходят в противофазе с колебаниями внешней силы. Амплитуда координаты равна:

Таким образом, колебания тела происходят по закону

При ω ⇒ ∞ (это эквивалентно условию ω >> ω₀)х_m ⇒ 0, т. е. амплитуда колебаний мала. Этот результат вполне естествен. Сила столь быстро меняет направление, что тело, обладающее инертностью, не успевает заметно сдвинуться относительно положения равновесия.

Половину периода внепхняя сила соверпхает положительную работу, а другую половину — отрицательную. Половину периода сила и перемещение направлены одинаково, а другую половину периода они направлены в противоположные стороны. Энергия опять почти не поступает в систему.

* Человек на качелях может самостоятельно раскачаться. Для этого он должен приседать при наибольших отклонениях качелей от положения равновесия и выпрямляться в положении равновесия. Такие колебания, называемые параметрическими, мы рассматривать не будем.

** Необходимо сделать одно уточнение. При наличии сил сопротивления собственная частота ω_c свободных колебаний не равна . На самом деле она несколько меньше:

Но при малом коэффициенте сопротивления (к ⇒ 0) ω_c = ω₀. Практически наиболее интересен именно такой случай. Поэтому мы с полным основанием можем считать собственную частоту колебаний системы равной ω₀.

Вынужденные колебания. Резонанс. Автоколебания

Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.

Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной ω , в то время как сама система совершает собственные колебания с той же самой частотой.

Установившиеся вынужденные колебания всегда происходят с частотой внешней силы. Частоту свободных колебаний определяют параметры системы.

Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время Δ t , прежде чем вынужденные колебания установятся. Это время будет равно тому времени τ , за которое затухают свободные колебания в данной системе.

В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ω 0 и вынужденные с частотой ω . Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.

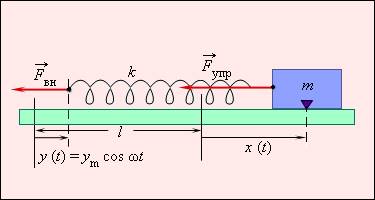
Разберем пример. У нас есть тело на пружине, совершающее вынужденные колебания (см. иллюстрацию ниже). Приложим внешнюю силу, обозначенную F → в н , к свободному концу пружины, после чего этот конец начнет перемещаться по закону, выражаемому формулой:

Здесь буквой ω обозначена круговая частота, а y m – амплитуда колебаний.

Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.

Рисунок 2 . 5 . 1 . Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой y = y m cos ω t , где l означает длину недеформированной пружины, а k –ее жесткость.

При смещении левого конца пружины на некоторое расстояние y и правого – на x по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:

∆ l = x — y = x — y m cos ω t .

В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:

m a = — k ( x — y ) = — k x + k y m cos ω t .

Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.

Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела a = x ¨ и его ускорением. У нас получится следующее:

x ¨ + ω 0 2 x = A cos ω t .

Эта зависимость называется уравнением внешних колебаний. Здесь ω 0 = k m является собственной круговой частотой свободного колебания, а ω – циклической частотой внешней (вынуждающей) силы.

Чтобы найти величину A для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:

A = k m y m — ω 0 2 y m .

То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.

Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:

x ( t ) = x m cos ( ω t + θ ) .

Здесь x m обозначает амплитуду вынужденного колебания, а буква θ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.

Если частоты очень низкие, т.е. ω ≪ ω 0 , то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что x ( t ) = y ( t ) . Сама пружина при этом практически не деформируется, а модуль внешней силы F → в н , приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.

Понятие резонанса

Резонанс – это резкое возрастание амплитуды вынужденных колебаний при сближении частоты внешней силы с собственной частотой колебания тела.

С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний x m и частотой вынуждающей силы ω .

Когда происходит резонанс, амплитуда x m может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности Q колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.

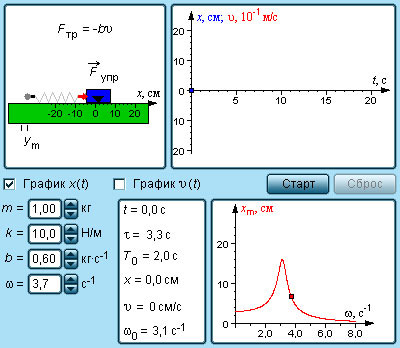
Рисунок 2 . 5 . 2 . Моделирование вынужденных колебаний.

Если добротность колебательной системы невысока (менее 10 ), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации 2 . 5 . 2 .

Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.

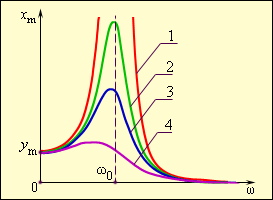
Рисунок 2 . 5 . 3 . Изображение затухания различных колебаний при помощи резонансных кривых: 1 — условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), 2 , 3 , 4 – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности ( Q 2 > Q 3 > Q 4 ) . Если частоты низкие, то ( ω ≪ ω 0 ) x m ≈ y m , а если высокие, то ( ω ≫ ω 0 ) x m → 0 .

Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.

Что такое автоколебательные системы

Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.

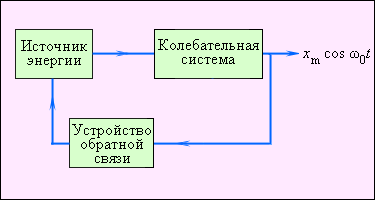
Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.

Рисунок 2 . 5 . 4 . Автоколебательная система со всеми основными составляющими.

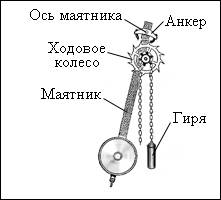
Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.

Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.

Рисунок 2 . 5 . 5 . Схема маятникового часового механизма.

Вынужденные колебания

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $\delta $ — коэффициент затухания; $<\omega >_0$ — циклическая частота свободных незатухающих колебаний (если $\delta $=0, то $<\omega >_<0\ >$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $\delta =\frac<2L>$ — коэффициент затухания; $<\omega >_0=\frac<1><\sqrt>$; $U=U_m<\cos \left(\omega t\right)\ >$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=\frac$ если колебания механические ($x_0=\frac-\ в\ случае\ электрических\ колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $\omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $\omega $.

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(\omega )$. Взяв производную $\frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($<\omega >_r$) равна:

При $<\delta >^2\ll <\omega >^2_0$ резонансная частота совпадает с собственной частотой колебаний $<\omega >_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $<\delta >^2\ll <\omega >^2_0$) амплитуда при резонансе равна:

где $Q=\frac<<\omega >_0><2\delta >$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Примеры задач с решением

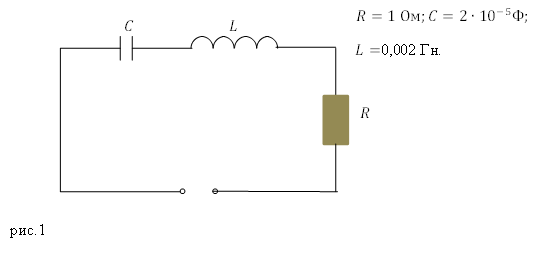
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=<\cos \left(\omega t\right)(Н).\ \ \ >$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $\delta =\frac<2m>$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна: